一种自动生成Wallace树形乘法器Verilog源代码方法

邓 建， 徐 洁

(电子科技大学 计算机科学与工程学院， 成都 611731)

0 引 言

Wallace树型乘法器[1]自上世纪60年代提出以来，由于具有并行性和低延迟的优点[2-3]，一直是通用乘法器[4-7]、数字信号处理(Digital Signal Process，DSP)中的乘法运算[8-10]、浮点运算[11]、模糊控制[12]和近似计算[13]等研究领域的热点。目前通常采用超高速集成电路，硬件描述语言(Very-High-Speed Integrated Circuit Hardware Description Language, VHDL)[14]或Verilog[15]来进行乘法器硬件的设计和仿真。

在文献[16]中讨论了Wallace树型乘法器的结构和设计，但在实验过程中发现：在8×8无符号位Wallace树型乘法器的Verilog源代码中存在3个错误；在后续的第9、10、11、13、14章使用了位数更多的Wallace树型乘法器，但书中未提供相应的Verilog源代码。为解决上述问题，根据文献[16]中的Wallace树型乘法器结构，设计了一个自动生成Verilog源代码的应用程序。

1 无符号位乘法器的工作原理

无符号位二进制数的乘法运算可以通过每两个二进制位相乘、移位和加法来实现。以两个两位无符号位数相乘为例，设a、b分别为两位无符号位二进制数，则

z=(a[1]a[0])×(b[1]b[0])=

(a[1]a[0])×b[0]+(a[1]a[0])×b[1]×21=

a[0]b[0]+(a[1]b[0]+a[0]b[1])×21+

a[1]b[1]×22

(1)

式(1)中有4个乘积项，每个乘积项可以通过逻辑“与”实现。如图1所示，如果a、b分别为8位无符号位二进制数，则总共有64个乘积项，图1中的每个 “●”代表一个乘积项。

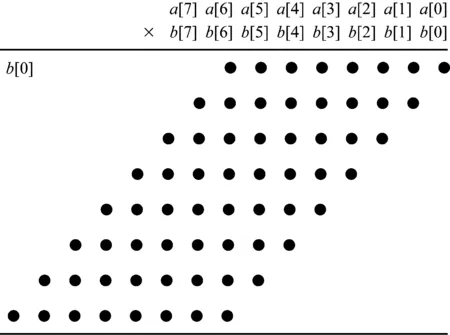
图1 8×8无符号位乘法器中的乘积项

设a、b分别为M和N位无符号位二进制数，则总共有M×N个乘积项。

2 Wallace树型乘法器的结构

对图1中的乘积项进行累加是乘法器中耗时最多的操作[3]，Wallace树型乘法器[1]采用分级并行累加的方法进行操作。图2是对图1中的乘积项进行第1级的并行累加结构图。

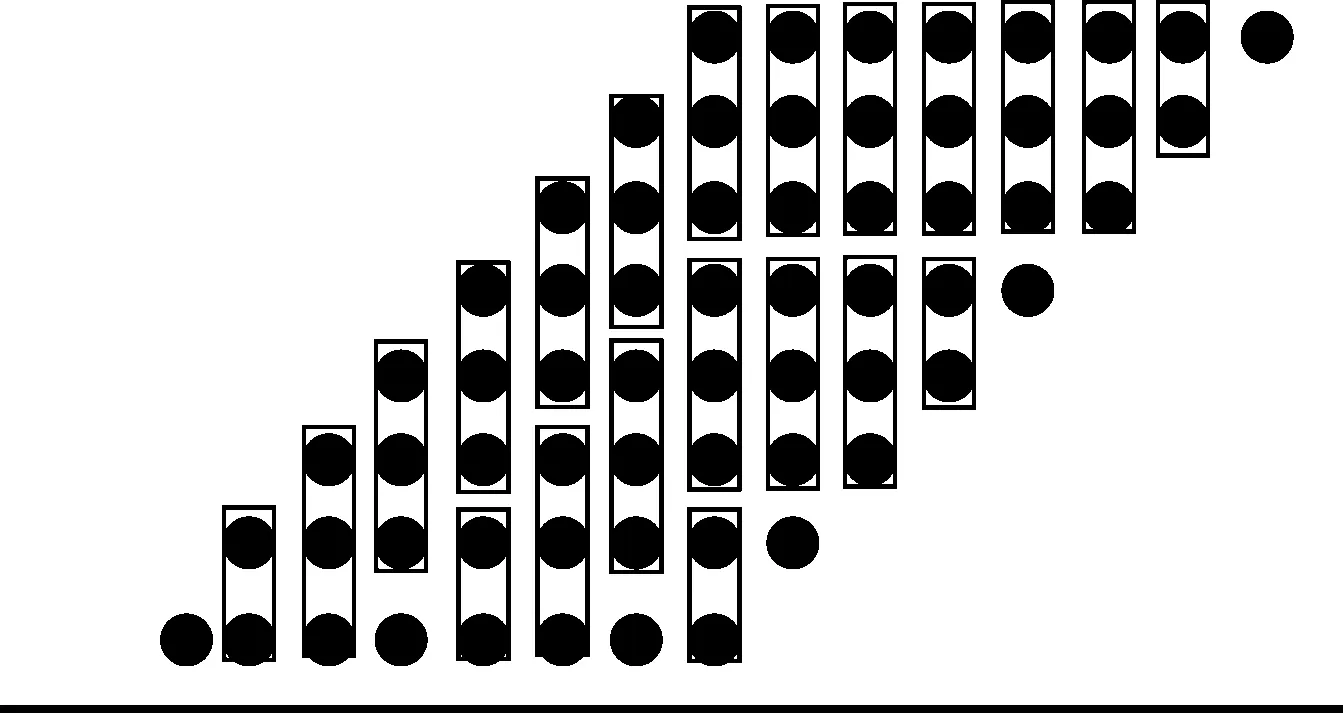
图2 8×8无符号位Wallace树型乘法器的第1级

图2中的每个方框代表一个加法器，方框内有3个 “●”使用全加器，方框内有2个 “●”可以使用半加器或全加器，不在方框中 “●”直接送到下一级。每个加法器输出一个向高位的进位、一个本位和。

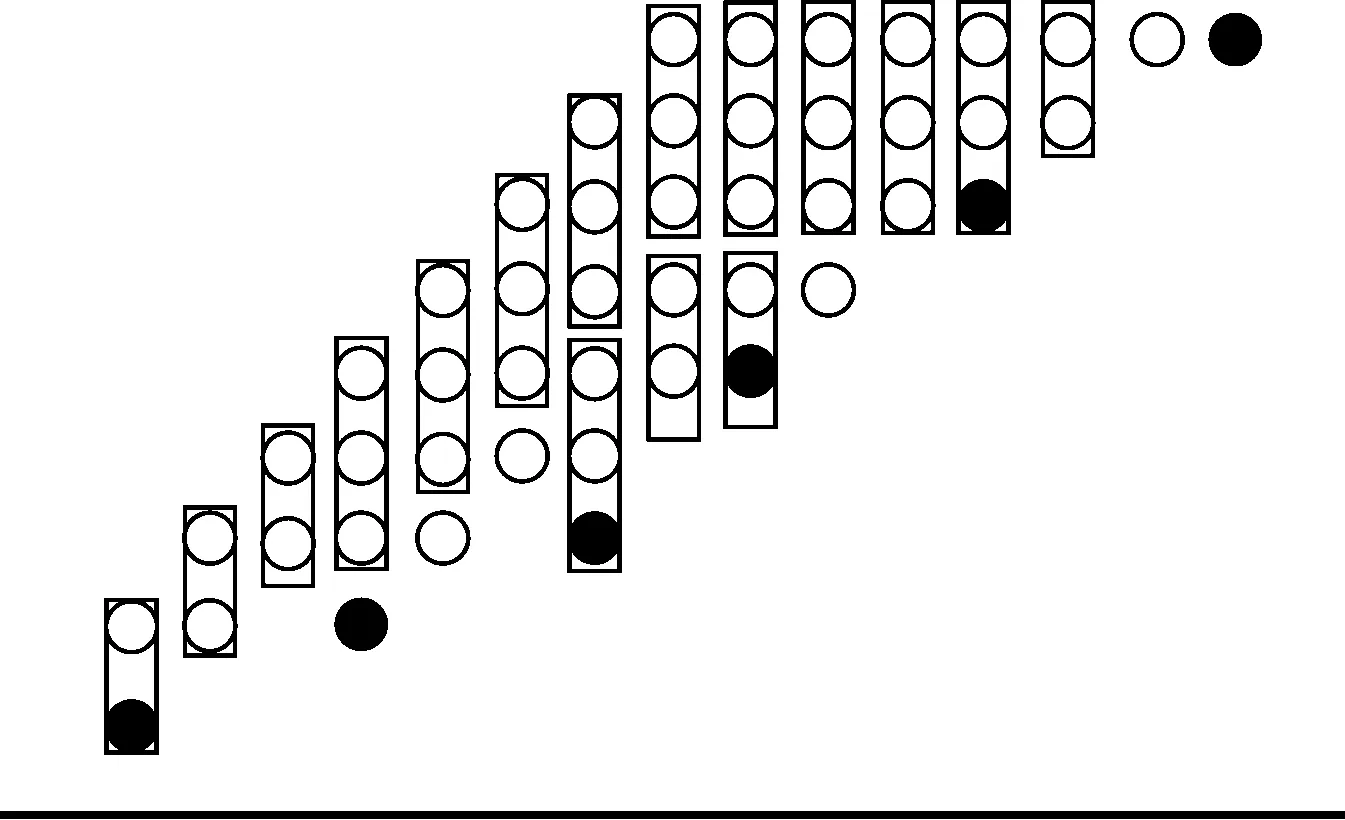
图3 8×8无符号位Wallace树型乘法器的第2级

在图2中，第1级共需要21个加法器，输出的21个向高位的进位、21个本位和，总共42个输出，它们作为第2级的输入。图3是第2级的结构图，图3中的“○”代表来自图2中加法器的输出。第2级的输出作为第3级的输入，第3级的输出作为第4级的输入，图4、5分别表示第3、第4级的结构。

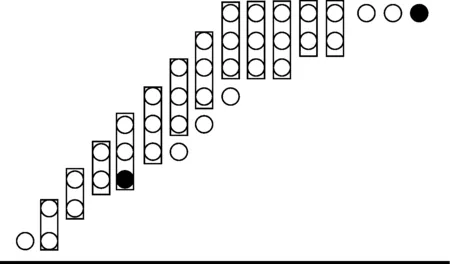
图4 8×8无符号位Wallace树型乘法器的第3级

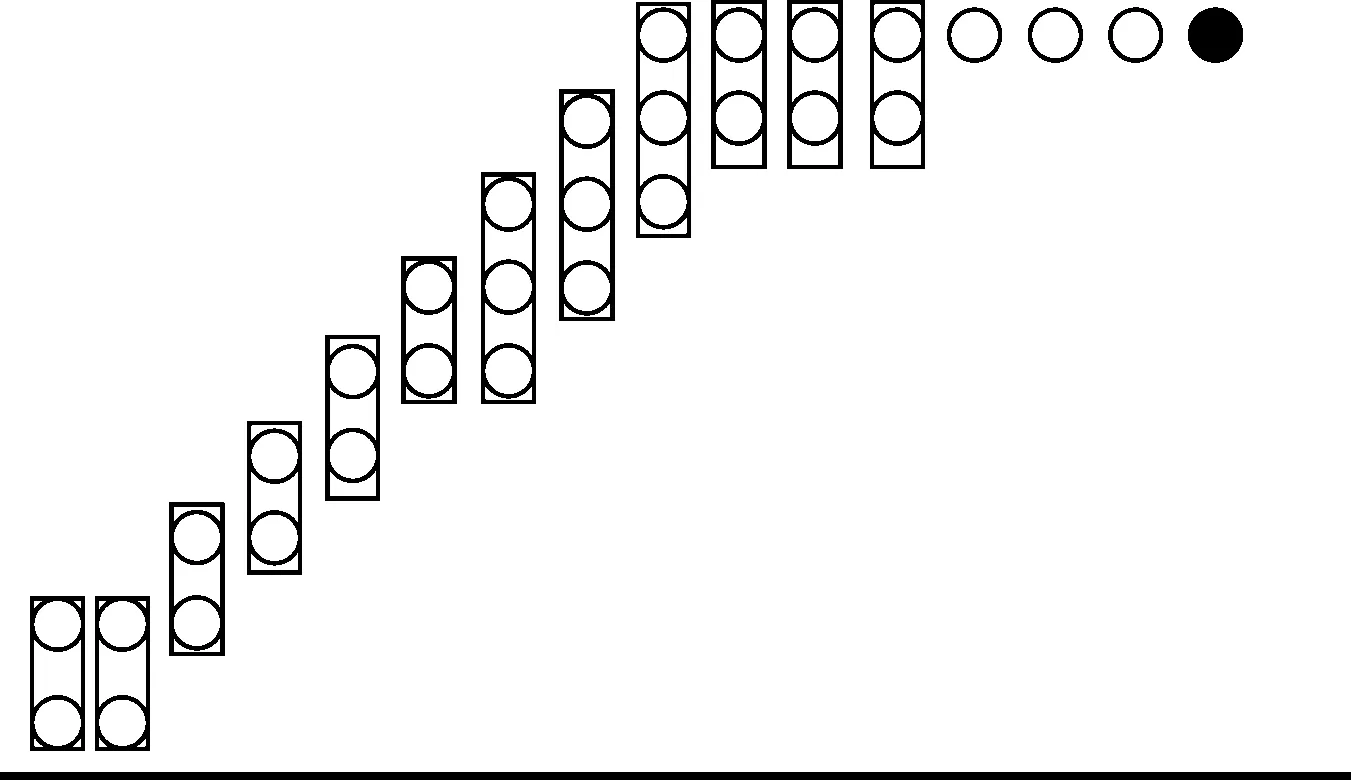
图5 8×8无符号位Wallace树型乘法器的第4级

图5中输出的第00-04位可以直接作为最终输出，第05-15位还需要送到输出级再做一次累加，图6为输出级的结构。图5、6中第15位向第16位的进位可以忽略。

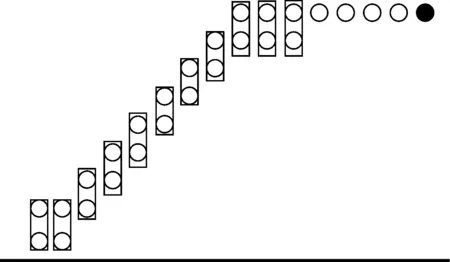
图6 8×8无符号位Wallace树型乘法器的输出级

3 Verilog源代码生成算法

Wallace树型乘法器由于乘积项和中间的加法器数量多，采用Verilog进行设计时工作量大。为提高设计效率，根据无符号位二进制数的乘法器的工作原理和Wallace树型乘法器的结构，设计了一个自动生成Verilog代码的应用程序。整体算法为:

GenerateWallaceTreeUnsigned(M,N, *FileName )

1. ifM=N

2. then modulename←"wallace_tree "+M

3. else modulename←"wallace_tree "+M+"x"+N

4. FileName ← modulename+ ".v"

5.fp← fopen(FileName， "wt+" )

6. GenerateFileHeader(fp， modulename，M，N)

7. products ← GenerateUnsignedProduct (fp，M，N)

8. product_tree←GenerateItemTree(M,N, products)

9. adder_tree ← new TList

10. level ← 1

11. success←GenerateAdderTreeTopLevel(fp， level， M, N， product_tree, adder_tree)

12. while success = TRUE

13. do

14. level ← level +1

15. success = GenerateAdderTreeNextLevel(fp， level，M,N， adder_tree)

16. OutputLastUnsigneLevel(fp，M，N， level )

17. if(fp≠NIL )

18. then fclose(fp)

算法中的第1～5步进行初始化工作，按照文献[16]第3章和第9章的源代码，生成对应的Verilog模块名称，创建Verilog源文件。第6步向输出文件输出Verilog代码的开始部分，包括模块和输入输出定义。第7步根据本文的图1和文献[16]第79页生成乘积项，并输出对应的Verilog代码。第8步创建树型乘法器每一级中加法器的输入变量名称，根据第7步生成的乘积项和本文的图2确定第1级结构中每个加法器所使用的乘积项名称。第9～11步创建Wallace树型乘法器的第1级，adder_tree中包含每级所使用的加法器的输入和输出变量名称，第12～15步循环创建后续每一级，直到不需要继续创建为止。第16步创建输出级。在创建Wallace树型乘法器的过程中，同时输出对应的Verilog代码。第17～18步关闭Verilog文件。

在本算法的基础上，根据文献[16]中第74～77页的方法编写带符号位的二进制Wallace树型乘法器。本算法可以很方便的生成位数更多的Wallace树型乘法器的Verilog源代码。

在文献[16]中第271～276页的浮点乘法器中要用到24×24位Wallace树型乘法器，书中只提供了Wallace树型乘法器的结构图，没有提供对应的Verilog源代码。采用本算法自动生成了8×8、24×24、24×26、24×28、26×24、26×26模块。如表1所示，随着位数的增加，由于乘积项变得更多，所以Wallace树型乘法器的级数更多。如果由设计人员手工输入，不仅效率低，而且容易出错。

表1 M×N位无符号位Wallace树型乘法器模块

4 实验仿真

采用Xilinx ISE 14.7版本设计软件，对自动生成的Verilog源代码进行仿真，输入数据a分别为0和255，输入数据b分别为0、1、2、4、8、16、32、64、255，得到与文献[16]第82页相同的仿真结果。

图7 8×8无符号位Wallace树型乘法器仿真结果[16]

但是图7中的测试数据太少，如果采用穷尽测试，编写双重循环，对0～255的每两个数进行乘法运算，发现文献[16]中的Verilog代码会出现运算不正确的情况。经过仔细核对，发现第80～81页的源代码共存在3处错误，经过修订后才能得到正确的结果。造成错误的原因估计是因为乘积项和中间加法器的输出项目多，手工输入源代码容易出错。采用本文提出的方法，自动生成Verilog代码，将Wallace树型乘法器的硬件输出与软件的乘法结果进行65536次穷尽对比，结果一致，没有发现错误。测试模块的算法如下：

wallace_tree8_tb

1. // Inputs

2. reg [7:0]a

3. reg [7:0]b

4. // Outputs

5. wire [15:0]z

6. wallace_tree8 uut (.a(a), .b(b), .z(z))

7. task Check ;

8. input [15:0] expect

9. if(z!= expect )

10. then

11. error_count ← error_count + 1

12. $display("error :a= %x，b= %x， expect %x， but the output is %x"，a，b， expect，z)

13. else

14. success_count ← success_count + 1

15. endtask

16. initial begin

17. error_count ← 0

18. success_count ← 0

19. for i from 0 to 255

20. do

21.a←i

22. for j from 0 to 255

23. do

24.b←j

25. #10 //延迟10ns

26. Check(i*j)

27. display("total_count = %d， success_count = %d， error_count = %d"， success_count + error_count， success_count， error_count )

28. end

在上述算法的第25步需要延迟10 ns，目的是等待Wallace树型乘法器的硬件结果。对于24×24、24×26、24×28、26×24、26×26模块，也进行了仿真，取得与文献[16]相同的结果。

5 结 语

本文提出了一种自动生成Wallace树形乘法器Verilog源代码的方法，可以克服人工输入源代码的错误，提高设计效率和质量。在以后的教学过程中，还可以在以下几个方面继续改进：① 增强对测试代码的重视，通过大量的测试来考察乘法器的输出是否正确；② 将乘法器下载到FPGA开发板上进行实际运行，分析其逻辑资源占用情况和延迟；③ 进一步改进Verilog代码生成算法，在生成的Verilog代码中自动增加注释。采用自动生成Wallace树形乘法器Verilog源代码的方法可以提高同学们的学习热情，愿意接受高难度实验项目的挑战。