基于ARIMA模型分析西安市鄠邑区HFRS疫情

杨祖荣,刘 昆,谭 新,吴克坚

(1空军军医大学流行病学教研室,西安 710032;2西安市鄠邑区疾病预防控制中心;3空军军医大学数理教研室;*通讯作者,E-mail:wukejian1983@163.com)

肾综合征出血热(hemorrhagic fever with renal syndrome,HFRS)又称流行性出血热,是由汉坦病毒引起,以高热、出血和肾功能损害为主要临床特征[1],是严重危害人类健康的自然疫源性疾病和重点传染病之一[2,3]。我国作为世界上HFRS发病人数最多的国家,拥有占世界报道病例数90%以上的累计病人数,内陆31个省、自治区、直辖市均有HFRS的病例报告[4],特别是在我国华北、东北的部分地区HFRS已成为当地危害最严重的传染病之一[5]。陕西省是我国HFRS疫情高发区,西安地区的鄠邑、周至、长安等区(县)是疫情的主要分布地,其中鄠邑区是HFRS疫情国家级监测点[6]。鄠邑区HFRS疫情的空间分布相对集中、人群分布以青壮年农民为主。自1994年对鄠邑区HFRS发病率较高的平原乡镇启动了HFRS疫苗接种计划,接种对象以15-60岁的人群为主[7]。为探究所采取措施是否具有针对性,本文基于求和自回归移动平均(autoregressive integrated moving average,ARIMA)模型对鄠邑区1971-01～2012-12的HFRS疫情数据进行分析。

1 材料与方法

1.1 资料

本研究1971-01～2012-12的HFRS疫情月度数据来自西安市鄠邑区疾病预防控制中心。

1.2 方法

1.2.1 ARIMA模型 ARIMA模型来自20世纪70年代美国Wisconsin-Madison大学的Box和Jenkins所著的TimeSeriesAnalysis:ForecastingandControl一书,主要用于分析时间序列,并对未来趋势进行预测。在ARIMA(p,d,q)模型中,AR代表自回归模型,I表示差分,MA代表滑动平均模型;p表示自回归阶数,d表示对含有长期趋势、季节变动、循环变动的非平稳时间序列进行差分处理的次数,q表示滑动平均的阶数[8]。ARIMA(p,d,q)模型的基本形式如下[9]:

(1)

1.2.2 模型建立 利用鄠邑区1971-01～2012-12每月HFRS发病数据建立数据库,通过R语言“tseries”和“forecast”软件包进行数据处理与分析,并建立ARIMA模型。根据时间序列图或自相关系数判断时间序列的平稳性,对非平稳时间序列进行差分处理平稳化,并利用自相关函数(autocorrelation function, ACF)图和偏自相关函数(partial autocorrelation function, PACF)图拟定模型p、q的阶数,对模型和参数的显著性进行检验,判断残差序列是否为白噪声序列;若不是白噪声序列则需再次调整差分阶数以充分提取样本信息。逐个检验估计的参数是否显著非零,若参数显著不为零,则认为构建的模型合理,可进行下一步的预测[11]。

1.2.3 模型比较 将1971-01～2012-12年每月HFRS发病数据代入对应的ARIMA模型进行拟合及预测,比较所建立模型的拟合优度及预测残差。

2 结果

2.1 HFRS流行特征

1971-2012年,陕西省西安市鄠邑区共报告人间HFRS患者12 702例,HFRS年发病率在1971-1990年间呈波动增长趋势。从1994年开始年发病率逐步降低,但近几年有回升趋势。其中,1984年年发病率出现峰值,高达298.65/10万(1 439例),2005年出现最低值9.53/10万(55例),见图1。疾病发生存在明显的季节性和双高峰特征,主高峰期出现在10-12月份(9 586例),占全年总病例数的75.47%,次高峰期出现在7月份,3月份发病率最低(见图2)。

图1 1971-2012年鄠邑区HFRS年发病率变化趋势Figure 1 The annual incidence of HFRS in the Huyi District from 1971 to 2012

2.2 模型分析

2.2.1 数据平稳化 根据疫苗接种情况将鄠邑区HRFS月度发病数据分成1971-01～1993-12、1971-01～2012-12和1994-01～2012-12三组,分别进行差分平稳化处理。

2.2.2 模型的参数估计 通过分析数据预处理后的自相关函数和偏自相关函数图,发现基于数据1971-01～2009-12建立的模型(记为模型Ⅰ)自相关函数在p=1,2,3时较大,偏自相关函数在q=1,2时较大,经计算确定函数模型为ARIMA(1,0,1)(0,1,0)12,根据参数估计的结果构建模型I为:

图2 1971-2012年鄠邑区HFRS月发病人数分布Figure 2 The monthly incidence of HFRS in the Huyi District from 1971 to 2012

(2)

其中xt代表HFRS病例发病人数。

基于1971-01～1990-12发病数据建立的模型,记为模型Ⅱ,经计算确定函数模型为ARIMA(1,0,1)(0,1,0)12,根据参数估计的结果构建模型Ⅱ为:

(3)

类似地,基于1994-01～2009-12发病数据建立的模型,记为模型Ⅲ,确定函数模型为ARIMA(2,0,1)(0,1,0)12,具体是:

(4)

2.2.3 模型的拟合优度检验 我们将时间序列原始数据和相应的拟合数据的差值定义为模型的残差序列,用残差序列判断模型的优劣:假如残差序列的自相关系数和偏自相关系数均在95%可信限以内,则残差为白噪声序列。经计算,模型Ⅰ、模型Ⅱ和模型Ⅲ拟合残差是一个围绕0波动的平稳序列,大部分残差值在2倍标准差范围内,且Box-Pierce统计量的P值均大于0.05,表明残差为白噪声序列,模型拟合程度较好。

2.3 模型评价

2.3.1 利用所建的模型Ⅰ对1971-01～2009-12鄠邑区HFRS月发病率进行模拟,并用实际发病率拟合,然后预测2010-01～2012-12的月发病率,利用预测值的残差(即真实值-预测值)进行模型检验。由图3可知,1971-01～2009-12月发病率的实际值与拟合值存在一定差异,但都在合理范围内波动。2010-01～2012-12的预测月发病率与实际月发病率在短期内基本相符,但随着时间的增加,模型的预测误差有增大的趋势,因此模型Ⅰ能比较合理地预测短期HFRS发病趋势。

图3 鄠邑区HFRS月发病率模型Ⅰ预测图Figure 3 Prediction of the monthly incidence of HFRS in Huyi District by model Ⅰ

2.3.2 根据建立的模型Ⅱ对1971-01～1990-12鄠邑区HFRS发病率进行模拟,用实际发病率拟合,并预测1991-01～1993-12的发病情况。同样地,用预测值的残差进行模型评价。1971-01～1991-12鄠邑区HFRS发病率观测值与拟合值基本相符,波动差异较小且都在合理范围内;HFRS发病率预测值曲线与实际值曲线吻合程度高,表明模型Ⅱ可以很好地模拟预测未接种疫苗时鄠邑区HFRS的发病情况(见图4)。

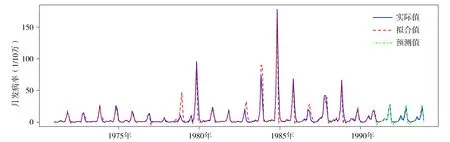
图4 鄠邑区HFRS月发病率模型Ⅱ预测图Figure 4 Prediction of the monthly incidence of HFRS in Huyi District by model Ⅱ

2.3.3 利用所建立的模型Ⅲ拟合1994-01～2009-12的HFRS月发病率,并对2010-01～2012-12的发病趋势进行预测,见图5。1994-01～2009-12鄠邑区HFRS月发病率观测值与拟合值在拟合前期(1994-1999年)有一定波动,产生了较小的差异,但都在合理范围内;而在拟合后期(2000-2009年)随着模型逐渐趋于稳定,观测值与拟合值基本相符;HFRS月发病率预测值曲线与实际曲线基本吻合,表明模型Ⅲ可以更好地预测该时期鄠邑区HFRS的发病趋势。

图5 鄠邑区HFRS月发病率模型Ⅲ预测图Figure 5 Prediction of the monthly incidence of HFRS in Huyi District by model Ⅲ

2.4 模型比较

通过对模型Ⅰ和模型Ⅱ的综合对比分析,发现对于同一个ARIMA模型(1,0,1)(0,1,0)12而言,模型Ⅱ的AIC值(1 922.72)明显小于模型Ⅰ的AIC值(3 452.76),由图3、图4也能发现模型Ⅱ拟合程度优于模型Ⅰ,其原因可能是模型Ⅰ是基于整体时间序列构建,未考虑疫苗的接种情况;而模型Ⅱ是基于疫苗接种前的时间序列而构建,未包含接种疫苗这一干预措施可能对时间序列造成的影响。由图6可知,模型Ⅱ预测残差的波动范围小,与HFRS的实际月发病率近似吻合,可见该模型可以对鄠邑区接种疫苗前的HFRS疫情做到很好的拟合及预测。

对模型Ⅰ和模型Ⅲ进行对比分析,发现接种HFRS疫苗后建立的模型Ⅲ,其AIC值、拟合程度明显优于模型Ⅰ(见表1)。通过比较模型Ⅰ和模型Ⅲ的预测发病率,并利用方差来描述预测残差的离散程度,发现模型Ⅲ的预测发病率更符合实际发病率(见图7,8)。

图6 模型Ⅱ HFRS月发病率预测残差图Figure 6 Prediction residuals of the monthly incidence of HFRS with model Ⅱ

表1模型Ⅰ与模型Ⅲ的拟合信息

Table1FittinginformationbetweenmodelⅠandmodelⅢ

模型AIC值残差方差预测方差 模型Ⅰ3452.7690.3022.96 模型Ⅲ948.937.346.37

图7 模型Ⅰ HFRS月发病率预测残差图Figure 7 Prediction residuals of the monthly incidence of HFRS with model Ⅰ

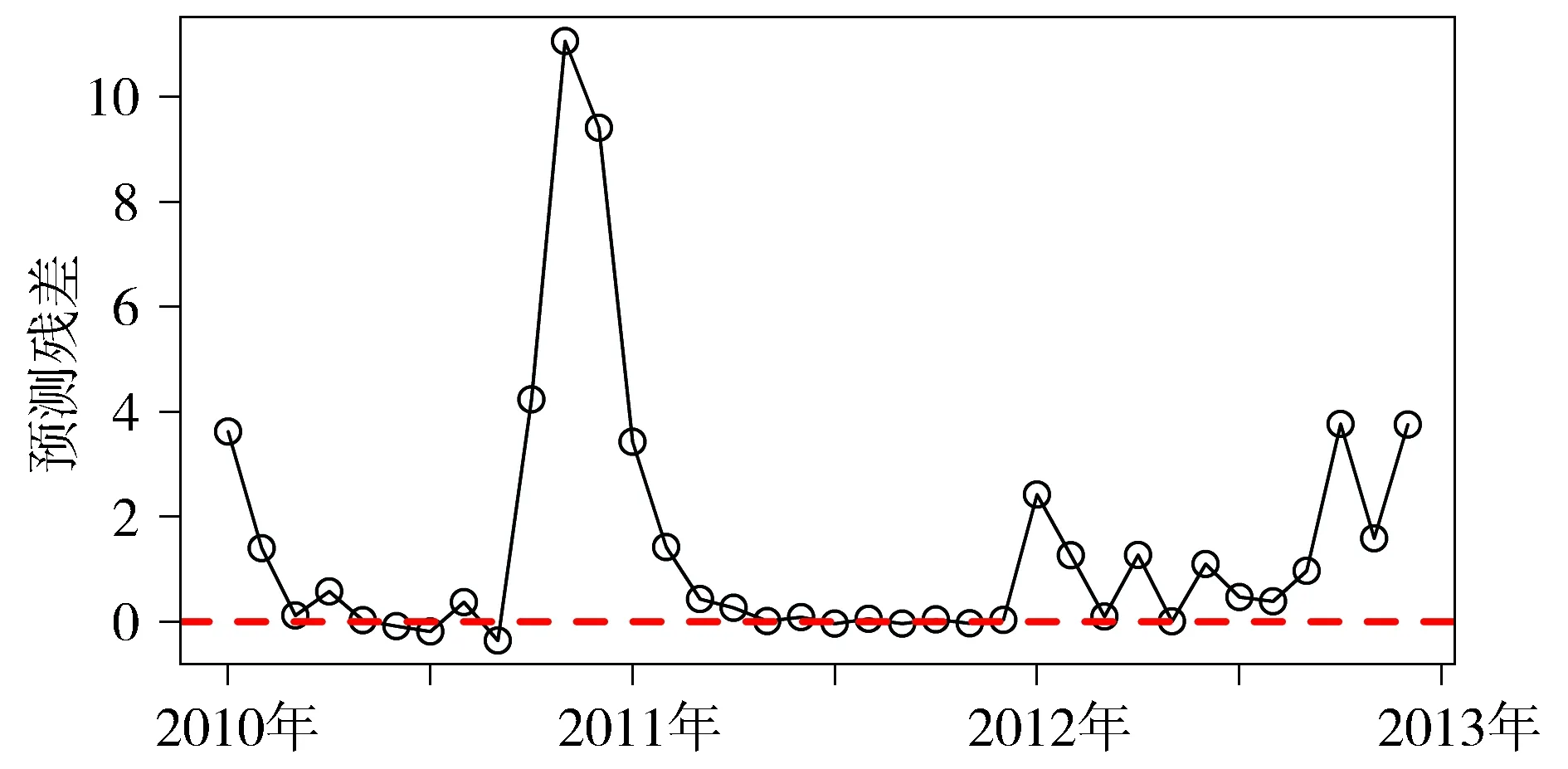
图8 模型Ⅲ HFRS月发病率预测残差图Figure 8 Prediction residuals of the monthly incidence of HFRS with model Ⅲ

3 讨论

本文利用陕西省西安市鄠邑区疾病预防控制中心提供的HFRS疫情数据,对1971-2012年鄠邑区HFRS新发病例的时间流行病学特征进行了描述性分析和模型分析。通过构建不同时间段的模型探讨了疫苗接种干预效果,分析了HFRS疫苗接种情况对HFRS疫情的防控作用。

根据鄠邑区报告HFRS新发病例及其趋势图,可以发现自1994年开始接种疫苗,鄠邑区HFRS发病率明显降低,疫情得到控制。然而近几年HFRS发病率有回升趋势,我们分析可能与外来务工人员的快速增长有关。随着经济发展,关中地区近年来外来务工人员数量庞大,该群体HFRS疫苗接种意识不强、疫情防护知识匮乏。这些因素提示我们应在6-7月份和10-12月的发病高峰前期开展针对性防病知识宣传教育,加大宣讲力度,并扩大HFRS疫苗接种范围尤其是对外来务工人员进行疫苗接种。

通过模型拟合及预测比较,发现模型Ⅰ对接种疫苗后的HFRS发病数据拟合程度变差,只有重新建模型才能更好地拟合、预测接种疫苗后的发病情况。当模型Ⅰ的自回归阶数p由1阶升到2阶后,模型再次较好地拟合疫苗接种后的HFRS发病数据,表明接种疫苗使HFRS疫情周期性分布的循环周期发生改变[12],因此可以认为疫苗的接种改变了HFRS疫情的发病趋势,对HFRS发病率的降低可能存在显著影响。

由于ARIMA模型可以综合考虑序列的趋势变化、周期变化及随机干扰,借助模型参数进行量化表达,能较精确地反映时间序列中所包含的动态依存关系,因而具有明显的优势和特色[13],同时也适用于各种复杂的时间序列,是一种实用性强、精确度高的短期预测方法[14]。本研究通过考虑时间序列与HFRS疫情的相关性、分组建模讨论了接种HFRS疫苗对疫情的影响,但建立的模型只适合进行短期较为准确的预测,并且疫情的传播是多种因素共同作用的结果,各因素之间存在着错综复杂的联系,很难运用结构式的因果模型进行预测。因此下一步,我们将综合考虑鄠邑区HFRS疫情发生的季节性、接种疫苗、温度、湿度、降水、地域特征和人群特征等因素,不断积累、添加新的监测数据,以便能获得更加准确的ARIMA模型,为鄠邑区HFSR疫情的防控提供理论指导,同时本研究也清晰地表明接种HFRS疫苗对HFRS疫情的防控存在明显的积极作用,但进一步加强HFRS防治工作,开展疫情监测和深入研究工作仍是HFRS防控工作的主要任务。