考虑低压释放特性的双机综合负荷模型参数识别策略研究

王 逸 ，姚李孝 ，赵 兵 ，贺 庆 ，马士聪

（1.西安理工大学，陕西 西安 710048；2.中国电力科学研究院，北京 100084）

0 引言

自21世纪以来，中国电网以前所未有的速度发展，形成了大规模、远距离、交直流混联特征。近年来风电、太阳能等新能源不断接入电网，更加恶化了电网的运行环境，给电网安全稳定监控带来了巨大挑战，电力系统仿真是电力系统安全稳定分析的重要手段，电力系统建模是电力系统仿真分析的基础。发电机、线路、变压器等电力元件能够建立详细的模型，而电力负荷建模相对比较滞后[1-3]。随着经济发展，电力负荷特性也发生了巨大变化，具有低压保护装置的负荷越来越多，空调类负荷不断增加，进一步恶化电网运行条件。因此建立适当的负荷模型有着重要意义[4-6]。

目前，在电力系统应用最广泛的负荷模型是综合负荷模型，综合负荷模型由两部分组成，静态部分由恒阻抗、恒电流和恒功率组成，动态部分由感应电动机组成，感应电动机可以分为双感应电动机模型和单感应电动机模型，目前主要用单感应电动机模型。对于单机模型来说，想要完全表征需要12个参数，单独参数有10个，双机模型参数是单机模型参数的2倍，要想识别这么多参数基本是不可能的[7-8]。研究表明双机模型的比单机模型更加准确，但是双机模型参数多，识别精度低，误差大，限制了双机模型的应用。

合理的简化策略可以提高参数辨识精度。一些参数对负荷模型动态特性影响比较小，并且和其他参数存在耦合关系，因此这些参数可以不参与辨识，直接取典型值。文献[9]提出了一种基于参数灵敏度与相关性分析的综合负荷模型参数辨识策略。文献[10-12]应用轨迹灵敏度法选取综合负荷模型的主导参数，该方法也是目前应用最广泛的方法。但是辨识方法主要集中在单机模型的参数识别，并没有对双机模型参识别做出分析。文献[13]从综合负荷模型参数入手，在保证负荷模型暂态特性响应行进的情况下提出参数识别的简化策略。文献[14]将电动机分为装有低压保护的感应电动机、易堵转的感应电动机和不易堵转的感应电动机模型，采用统计综合法建立符合模型，是另外一种三机模型，描述电压恢复过程。文献[15]通过对负荷模型静态特性、动态特性、重启动特性和退出特性分析，将感应电动机分为4种，模型更加详细，也更加接近实际情况。这两种建模方法本质上也是双机模型的一种。

本文提出一种考虑低压释放的双电动机机综合负荷模型，将感应电动机分为易堵转的感应电动机和不易堵转的感应电动机。并通过轨迹灵敏度分析得出双机模型参数不能一起识别的结论，再通过对单机模型和双机模型结构的分析，提出了固定大电动机参数，识别小电动机参数的识别策略。通过算例仿真验证了识别策略的有效性。

1 考虑低压释放特性的双机综合负荷模型

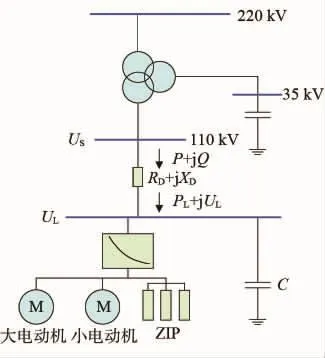
图1 考虑低压释放特性的双机综合负荷模型

考虑低压释放特性的双机综合负荷模型（SLM）如图1所示。该模型主体由恒阻抗＋恒电流＋恒功率（ZIP）和三阶感应电动机模型组成。静态部分与传统的综合负荷模型一样，动态部分由小电动机（易堵转的感应电动机）和大电动机（不易堵转感应电动机）组成。低压释放特性由有功低压保持系数和无功低压保持系数体现，有功低压保持系数和无功低压保持系数是电压的二次函数，其计算如式（1）～（5）所示。

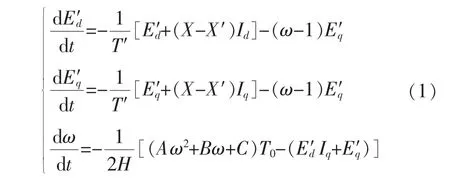
低压有功保持系数为

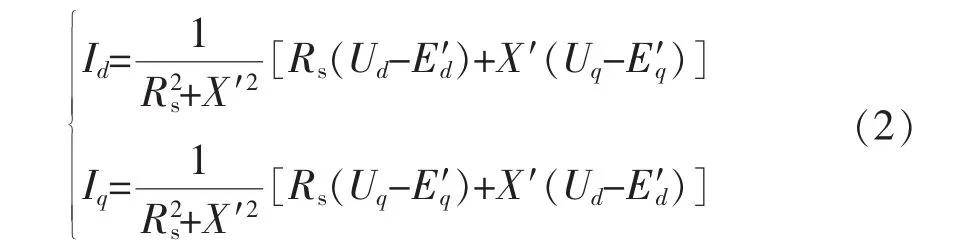
式中：E′d和E′q分别为感应电动机d轴和q轴暂态电势；Id、Iq、Ud和Uq分别为感应电动机 d 轴和 q 轴的电流及电压分量；ω为感应电动机转子转速；A、B和C分别为感应电动机的负荷力矩系数；T′为感应电动机在额定转速下的机械转矩；H为感应电动机的惯性时间常数；X和X′分别为感应电动机的同步电抗和暂态电抗；RS为感应电动机的定子电阻。

动态部分所吸收功率表达式为

静态部分满足的表达式为

式中：Pm为感应电动机有功功率；Qm为感应电动机无功功率；Ps为静态部分有功功率；Qs为静态部分无功功率；Ps0为静态部分初始有功功率；Qs0为静态部分初始无功功率；PZ、PI、Pp为有功功率系数；QZ、QI、Qp为无功功率系数。

当负荷电压降落负荷低压释放阈值上限时，并在持续低电压，电动机的负荷表达式仍为式（4），此时负荷所吸收的功率表达式为

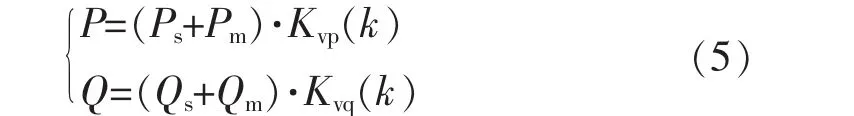
式中：Kvp为低压有功保持系数；Kvq为低压无功保持系数。

低电压有功无功保持系数计算如式（6）～（7）所示，其中k为仿真时刻，用电压相对于初始电压的标幺值表示，Ulimb为释放起始阈值，Ulime释放结束阈值，U 为电压值，afp、bfp、cfp有功电压相关系数，afq、bfq、cfq为无功电压相关系数。

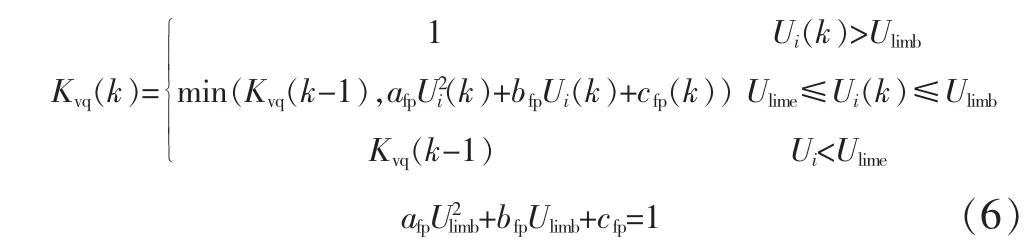
低压无功保持系数为

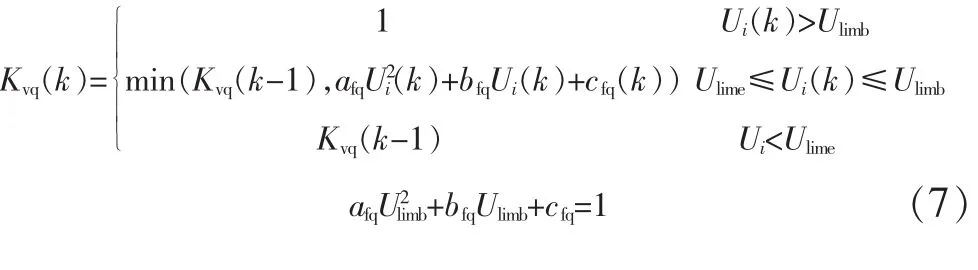
2 单机模型和双机模型适用性分析

等值感应电机可以分为单机负荷模型和双机负荷模型。单机负荷模型是将负荷中所有的感应电机聚合为1台等值电动机。双机负荷模型是按照感应电动机稳定性将聚合为2台等值电动机，即将稳定性差（即小电动机）的聚合为1台感应电机，稳定性好（大电动机）的聚合为1台感应电机。根据上述负荷模型可知，单机模型所需要识别的参数有12个。文献[16]对单机模型识别策略简化分析做了许多研究。单机模型的识别精度较高。而双机模型参数求取主要采取统计综合法求取，统计综合法必须有详细的负荷数据，获取和统计比较困难，对于双机模型的参数辨识策略研究很少。

220 kV变电站所带负荷可分为3类：工业负荷、商业居民负荷、农业负荷，这3类负荷中每种感应电动机的比例在一定的范围内，因此可以通过划分变电站类型来确定采用单机模型还是双机模型。将220 kV变电站分为6类：普通工业负荷、商业居民混合负荷、工业居民商业混合负荷、工业居民农业混合负荷、居民商业农业负荷、高耗能负荷，分类依据如表1所示。

在建立华东电网综合负荷模型的过程中，发现普通工业负荷建立的单机模型比较精确，与实际相接近，而对商业居民混合负荷、工业居民商业混合负荷、工业居民农业负荷、居民农业负荷建立的单机综合负荷模型精度较差。通过对4种负荷进行对比发现普通工业负荷主要以工业大电动机（即不易堵转的感应电动机）为主，居民商业混合负荷主要以小电动机（即易堵转的感应电动机）为主，因此单机模型误差较小，仿真结果较好。但工业居民混合负荷和工业居民农业混合负荷中工业大电动和工业小电动机比例相差不大，因此单机模型仿真效果较差。综上所述，对于普通工业负荷和居民商业负荷变电站应采用单机模型建模，对于工业居民商业混合负荷和工业居民农业混合负荷应采用双机模型建模。

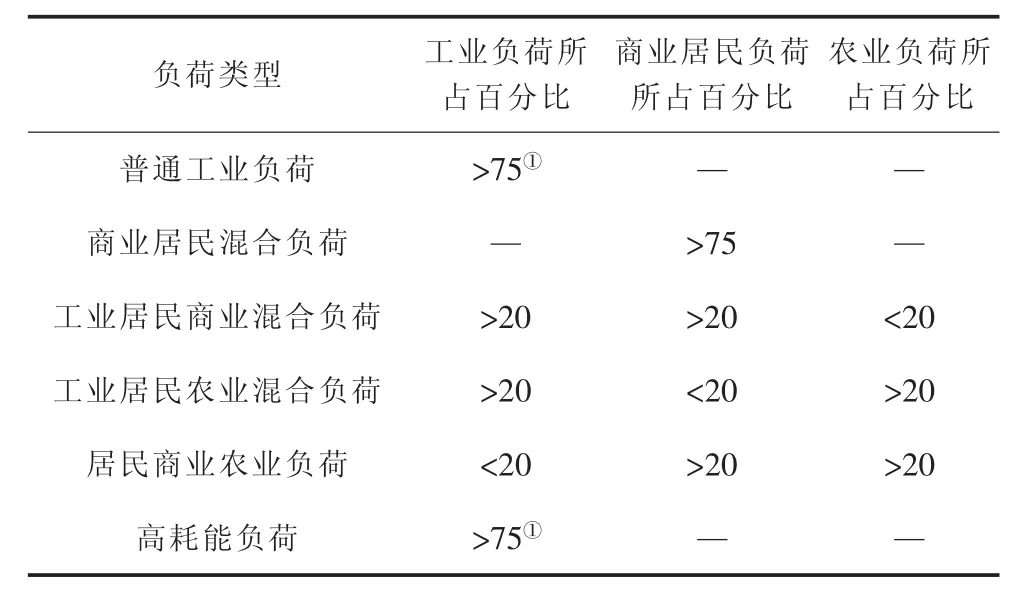
表1 220 kV变电站负荷分类原则 %

3 双机参数辨识策略分析

3.1 双机模型的灵敏度分析

轨迹灵敏度法可以计算负荷参数对负荷动态响应的灵敏度。轨迹灵敏度在电力系统应用日益广泛。灵敏度分析法的详细介绍可参照文献[12]。通过灵敏度分析可知，如果参数之间存在相关性，则这些参数的灵敏度曲线同时过零点。如果几个参数的轨迹灵敏度曲线同时经过零点，则这几个参数是不可以区分的。如果所有参数的灵敏度曲线都不同时经过零点，则所有参数基本上是可以区分的。轨迹灵敏度均值越大，参数越容易辨识。

根据轨迹灵敏度理论，以IEEE-39节点系统为例，IEEE-39节点如图2所示，对双电动机负荷模型参数进行轨迹灵敏度分析。系统参数设置为：母线3、4、15、16、18、21、23、25 处设置同一套参数的 CLM负荷， 母线 7、20、26、27、28 处设置同一套参数的SLM负荷，母线24、29、39处设置同一套参数的SLM负荷。双电动机负荷位于母线8上，在联络线4-14中间设置三相短路故障，3个周波后故障消失，观测变量为联络线7-8上的有功功率。根据轨迹灵敏度计算方法，进行多次系统仿真，计算绘制出轨迹灵敏度曲线和灵敏度均值，如图3及表2所示。

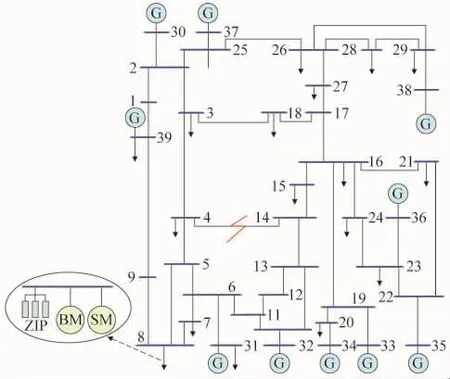
图2 10机39节点系统

图3（a）为感应电动机比例参数Pmp的估计灵敏度曲线图，其余参数的灵敏度曲线如图3所示。

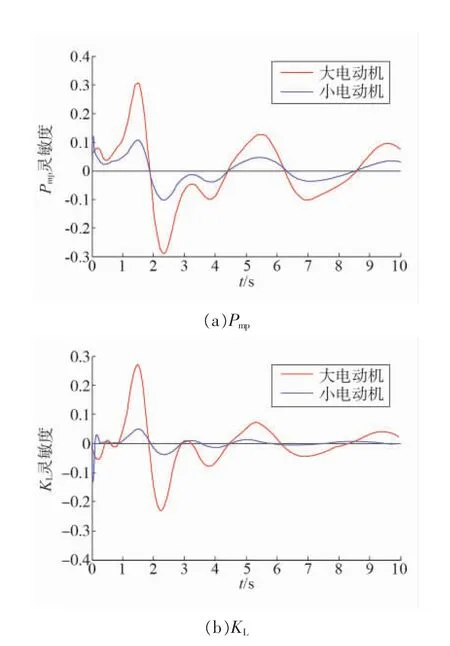
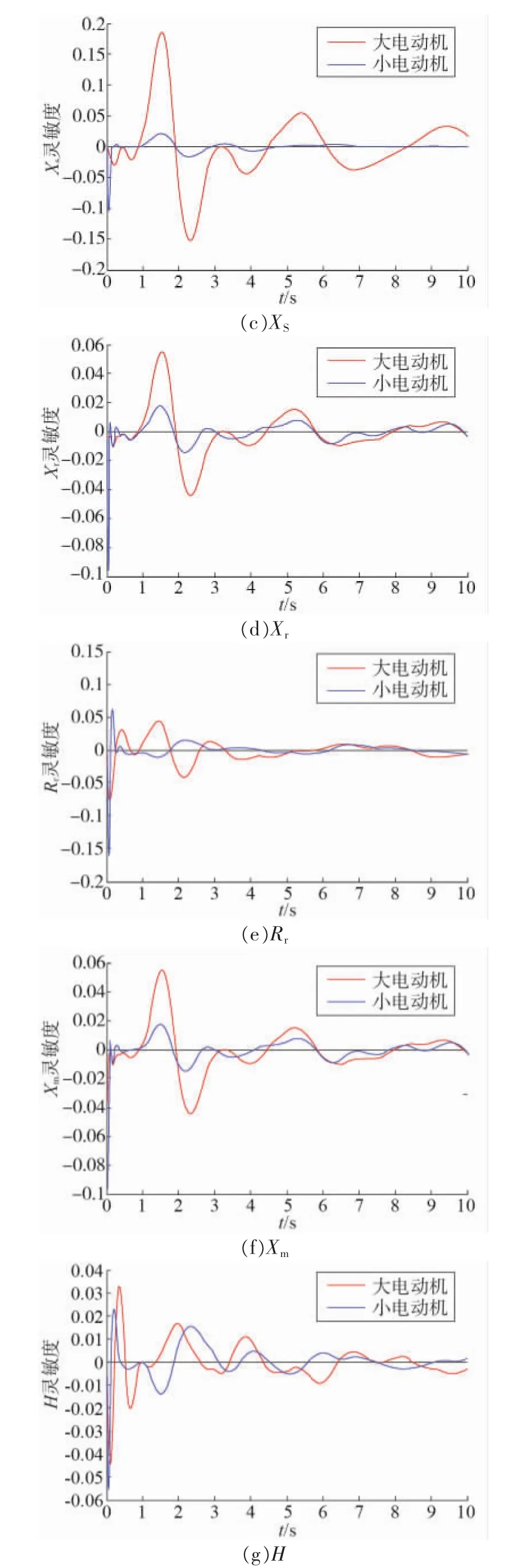
图3 各参数的灵敏度曲线

表2是电动机参数的灵敏度均值，从表2中可以看出两个电动机的感应电动机比例Pmp、初始负载率KL和定子电抗XS的轨迹灵敏度均值较大，较容易辨识，但轨迹灵敏度曲线基本是同时过零点的，可以认为是不可区分的；两个电动机的转子电阻Rr、转子电抗Xr、激磁电抗Xm和惯性时间常数H的轨迹灵敏度均值较小，不易辨识，但轨迹灵敏度曲线不完全同时过零点，是可以区分辨识的。因此不易堵转的电动机和易堵转的感应电动机的参数是不能一起辨识的。

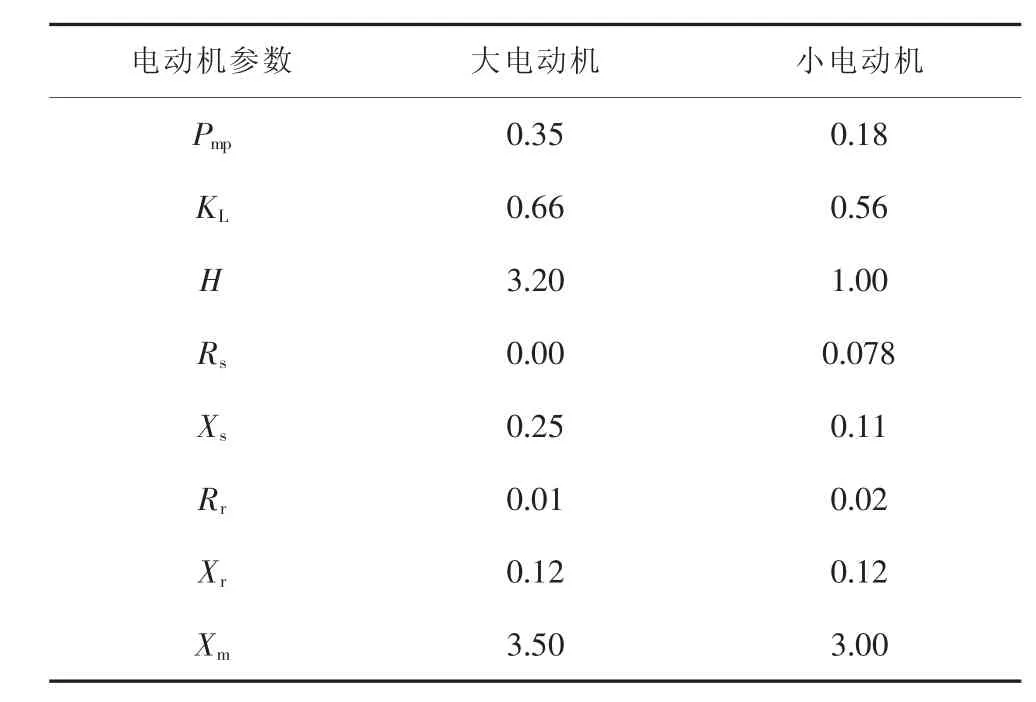
表2 电动机参数轨迹灵敏度均值

3.2 双电动机辨识策略分析

从双电动机负荷模型的结构和参数可以看出，等效大电动机的参数与传统负荷模型中的等效电动机的参数是类似的，说明二者的动态特性基本一致。而等效小电动机的参数与传统负荷模型中的等效电动机的参数差别很大，说明二者具有不同的动态特性。从实际系统构成来看，以工业电动机等为主的大电动机负荷一般具有较完备的低压保护装置，具有较强的躲过母线处的暂态低电压的能力；以空调负荷等为主的小电动机负荷耐低压能力差，易出现失速和堵转现象。在暂态低电压过程中，小电动机的动态特性是描述低电压释放等现象的主要因素。综上所述，等效小电动机的参数可视为双电动机负荷模型的关键参数。由轨迹灵敏度分析可知，双电动机负荷模型中大电动机和小电动机的参数不是完全可区分的，因此本文采用辨识关键参数的策略，即大电动机参数采用推荐值，小电动机的 Xs、Rr、H、KL作为重点参数进行识别，其他参数取典型值。

3.3 双电动机辨识方法

采用改进遗传算法进行参数识别。辨识采用的自适应度函数为

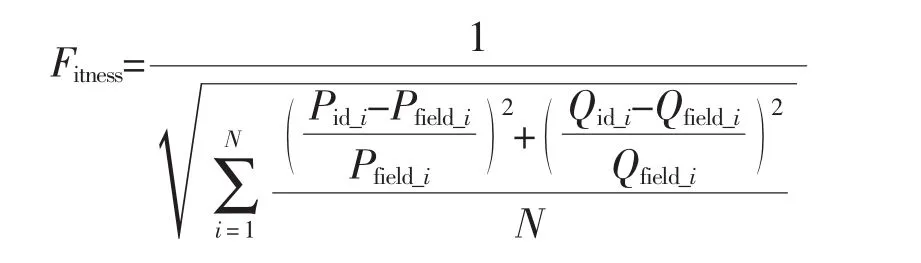
式中：Pid_i和Qid_i分别为辨识得到的第i个点的有功和无功；Pfield_i和Qfield_i分别为量测到的第i个点的有功和无功；N为采样点数量。辨识参数集选为定子电抗Xs、初始负载率KL、感应电动机比例Pmp和惯性时间常数H，其他参数选典型值。

改进遗传算法的辨识流程如图4所示。

图4 改进遗传算法辨识流程

4 算例分析

为了验证本文提出的基于电动机低压释放负荷模型的参数辨识策略，以华东某220 kV变电站为例，并将本文所用的方法与单机综合负荷模型相比较。根据前文模型参数的求解方法，可以求得有功系数取值为 afp=1.12、bfp=-0.660、cfp=0.828， 无功系数取值为 afq=1.335、bfq=-0.745、cfq=0.756，小电动机的参数辨识值为 Xs=0.095，KL=0.614，Pmp=0.332，2H=1.18。仿真曲线如图5所示。

从图5中的电压、有功功率和无功功率曲线可以看出采用固定大电动机参数，辨识小电动机重点参数的策略要比单机模型更加接近原系统，能够获得更高的仿真精度，使得负荷模型更加接近实际系统，提高了电力系统仿真精度。为电力系统更加科学运行和规划提供了保障。

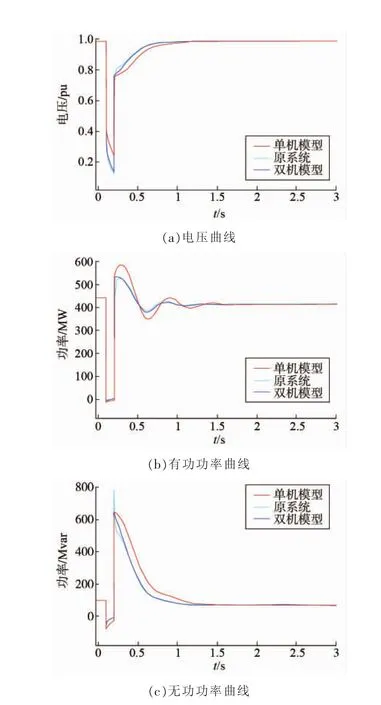
图5 双机模型参数识别结果

5 结语

介绍考虑低压释放特性的综合负荷模型，通过变电站负荷中感应电动机类型，并综合考虑误差和识别参数个数，得出对于负荷中感应电动机较为单一的220 kV变电站采单机模型可以得到更高精度的负荷模型，对于负荷中感应电动机类型比较复杂的220 kV变电站采用双机模型更加精确。通过轨迹灵敏度分析得出双电动机参数不能一起识别，并通过双机负荷模型结构和单机负荷模型结构分析，并采用了固定大电动机参数，识别小电动机参数，通过仿真分析可知采用这种策略识别精度较高，能够获得更加精确的负荷模型，提高电力系统仿真精度。