两种策略解决向量数量积问题

陕西 高 洁

平面向量的数量积求值、范围问题是重难点内容，也是高考的热点内容，常考常新．教学中我们强调学生应该具备基底意识或坐标化的思想，从而通过数化解决问题．平面向量具有代数和几何的双重属性，是沟通代数与几何的桥梁，而学生恰恰对形的应用有障碍，所以教学中还应该充分利用图形把问题置身于几何模型中，使得问题直观化，往往有意想不到的效果．本文给出几道数量积问题的题目，通过数和形上的解决，希望读者从中受到启发，选择合适的方法．

一、数量积计算问题

( )

策略一：转化为基底运算

策略二：借助数量积的几何意义

【点评】研究向量数量积的计算问题，如果通过数，一般有两个思路，一是建立直角坐标系，利用坐标研究向量数量积；二是利用一组基底表示所有向量，两种思路实质相同，取决于问题是否容易坐标化．如果利用数量积的几何意义，借助于几何运算会有意想不到的效果，但前提是某些射影容易计算．

策略一：转化为基底运算

策略二：转化为坐标运算

【解法2】以B为坐标原点，BA所在直线为y轴，BC所在直线为x轴，容易得到:

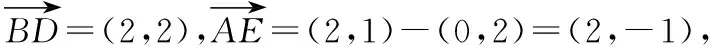
策略三：借助数量积的几何意义

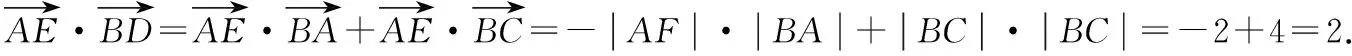
【点评】本题和例1是同一类问题，相对例1更容易坐标化，所以衍生出三个方法．

二、数量积范围和最值问题

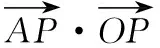
策略一：转化为基底运算

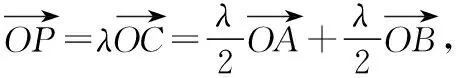
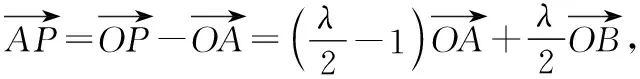
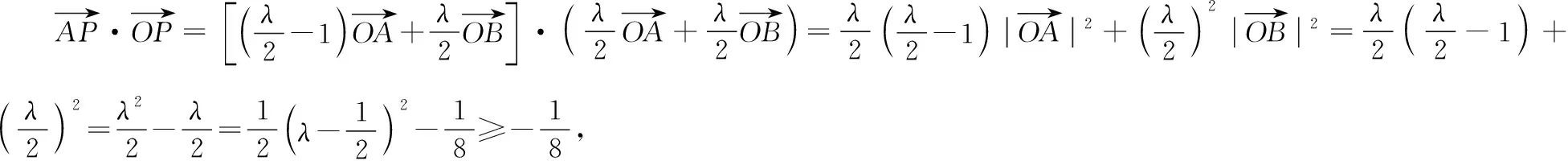
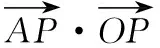
策略二：借助数量积的几何意义

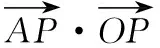
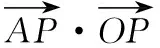
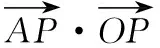
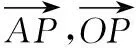
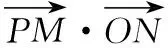
策略一：转化为坐标运算

策略二：借助数量积的几何意义

三、数量积问题的应用

( )

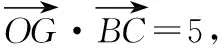
A．锐角三角形_______ B．钝角三角形

C．直角三角形_______ D．上述三种情况都有可能

策略一：转化为基底运算

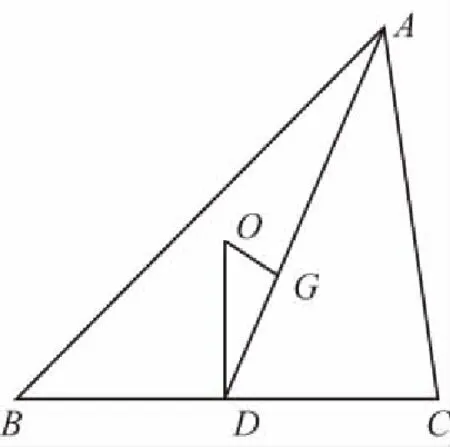
【解法1】如图所示，取BC的中点D，连接GD,OD，

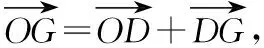
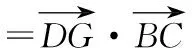
∴|BC|2+|AC|2<|AB|2，

即角C为钝角，△ABC是钝角三角形，选B．

策略二：借助数量积的几何意义

【解法2】如图，过G点作BC的垂线，垂足为E，过A点作BC的垂线，垂足为F．

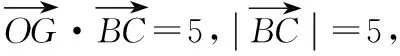
∴点E在线段DC上，

即DE=1，

∵△DGE与△DAF的相似比为1∶3，

可得DF=3，

∴F在线段BC的延长线上，

即角C为钝角，△ABC是钝角三角形，选B．