基于改进A*算法机器人路径规划研究

，

(青海民族大学计算机学院，青海 西宁 810008)

0 引言

导航是智能机器人非常重要的功能，也是机器人领域的一个研究重点。路径规划技术作为导航的核心，其主要任务是通过机体搭载的传感器获取周围环境信息，根据已知信息规划出一条从起始点到目标点的最优路径[1]。近些年来，针对机器人路径规划，诸多学者通过展开大量研究，提出各种面向不同场景的路径规划技术。其中比较著名的有快速搜索随机树[2-3]，概率路图法[4]，也有基于节点搜索的A*算法和D*算法[5-6]，基于启发式的遗传算法，粒子群算法和蚁群算法等[7-9]，还有应用于局部路径规划的动态窗口法和人工势场法等[10-12]。全局路径规划的前提是机器人需要有完整地图信息，而局部路径规划中机器人只需要知道局部信息，即通过传感器获得的自身周边障碍物信息。

在静态环境中A*算法是搜索最短路径最有效的算法，因此被广泛应用于实际路径规划中。由于该算法本身搜索原理的限制，规划出来的路径虽然效率高，但是转折点较多，对于移动机器人来说不利于直接执行。文献[13]提出一种平滑A*算法，旨在解决栅格环境下移动机器人A*算法规划出的路径折线多，转折次数多和转折角大的问题，最终获得了较优路径，该改进算法只是优化了路径，并没有减少路径长度，机器人执行时所付出的代价相差不大，同时也不具备很好的动态避障能力。文献[14]将人工势场法和蚁群算法进行融合，在栅格环境中，以人工势场法的规则信息作为蚁群算法寻优的基础，引入势场合力作为蚂蚁搜索路径点的部分启发信息，该方法解决了人工势场法容易陷入极值点的缺点，但是计算复杂度太大。动态窗口法实时性好，具有良好的躲避障碍物能力，但是该方法只是一种局部路径规划，并没有考虑到机器人的全局路径规划信息，使得最后规划出来的全局路径并不是最优。

基于以上各方法的特点，本文提出一种A*算法的改进方法，对邻域进行扩展，并且将启发式函数进行修改以适应具体环境需求，使传统A*算法能够更加灵活，规划出来的路径转折点少，同时全局路径更加平滑。将改进A*算法和动态窗口法进行结合，将两种算法的优点结合起来，既能进行全局最优路径的搜索，也让算法具备良好的避障能力，躲避障碍物。

1 改进A*算法

1.1 传统A*算法介绍

传统A*算法是一种标准的启发式函数，是静态环境中寻找最优路径的有效方法，其核心在于一个估价函数。从初始节点开始，按照启发函数对周围的节点开始搜索，选取周围最优的一个节点进行扩展，重复这一过程，直到搜索到目标点，然后由目标点回溯到起始点形成一条全局规划轨迹。其估价函数为：

f(n)=g(n)+h(n)

(1)

其中:f(n)是估计函数，表示的是从起始点到目标点的评价估计量，g(n)表示的是初始点到当前节点的实际代价值，而h(n)则表示当前节点到目标点的估计代价值。若将启发式函数设置成零，即h(n)=0，估价函数就完全由代价函数g(n)决定，此时A*算法就退化为基于贪心策略的Dijkstra算法，搜索效率大打折扣。h(n)启发函数直接决定了A*算法是否高效，h(n)中包含越多的启发式信息，A*算法效率就高，在搜索较少节点的情况下就可以找到最优全局路径，反之，若启发式信息量越少，规划出的轨迹就离最优轨迹相差越远。

1.2 邻域扩展

传统的A*算法只能向节点周围8邻域进行扩展，这种情况下机器人只能沿着八个方向运动，每个方向之间至少有四十五度的夹角，这就限制了机器人的运动，直接导致最终规划出的全局路径转折节点多，轨迹不够平滑。如图1所示，本文将8邻域搜索扩展到24邻域，机器人能够以更小的角度行进，从而使轨迹更加平滑。

图中中心黑色圆点表示目前机器人所在位置，传统方法中，机器人只能向8个方向扩展，即扩展到图中小圆点所在位置，扩展后一共可以向16个方向进行搜索，扩展点为图中24个箭头所在位置。传统A*算法中，由于搜索的节点数目较少，很可能传统A*算法中，由于搜索的节点数目较少，在前期就将更优秀的节点从列表中删除，从而只能找到次优路径，扩展后的算法由于搜索的节点更多，在很大程度上可以避免这种情况的发生，进一步优化了路径。

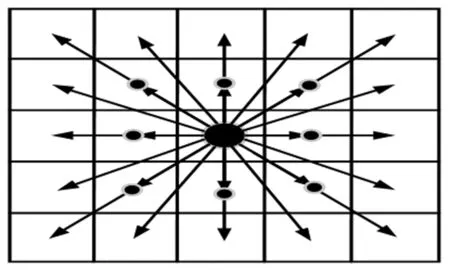
图1 24邻域扩展节点示意图

1.3 启发式函数的优化

在A*算法中，传统的启发式函数采用曼哈顿距离或者欧式距离。曼哈顿距离是指两个坐标点之间横轴和竖轴绝对值之和，假设每个相邻单位之间的路径代价为C，n表示当前点，goal表示目标点，可以得到基于曼哈顿距离的启发函数为：

h(n)=C*(abs(nx-goalx)+abs(ny-goaly))

(2)

若机器人单位可以进行任意方向的移动，我们就可以用欧式距离来表示对应的启发函数。欧氏距离指的是两点之间的直线距离，假设机器人经过单位长度的路径的代价为C，则欧式距离的启发函数为：

(3)

但是由于A*算法基于栅格地图，机器人不能全向移动，所以在实际应用中，这种启发式函数需要进行转化，速度较曼哈顿慢，但是路径更短。

基于上述24邻域优化，本文提出一种新的启发函数，更真实的描述节点扩展之后的代价，假设单位节点代价函数还是C，改进后的启发式函数如下。

若:|ny-goaly|≥|nx-goalx|:

(4)

若:|ny-goaly|<|nx-goalx|:

(5)

1.4 轨迹平滑

采用全局路径规划算法得到的路径有时候会歪歪扭扭，不利于机器人的执行，因此需要对路径进行处理，例如本文中对路径中某些冗余节点进行删除，并将更优的路径选择出来。轨迹平滑示意图如图2所示。

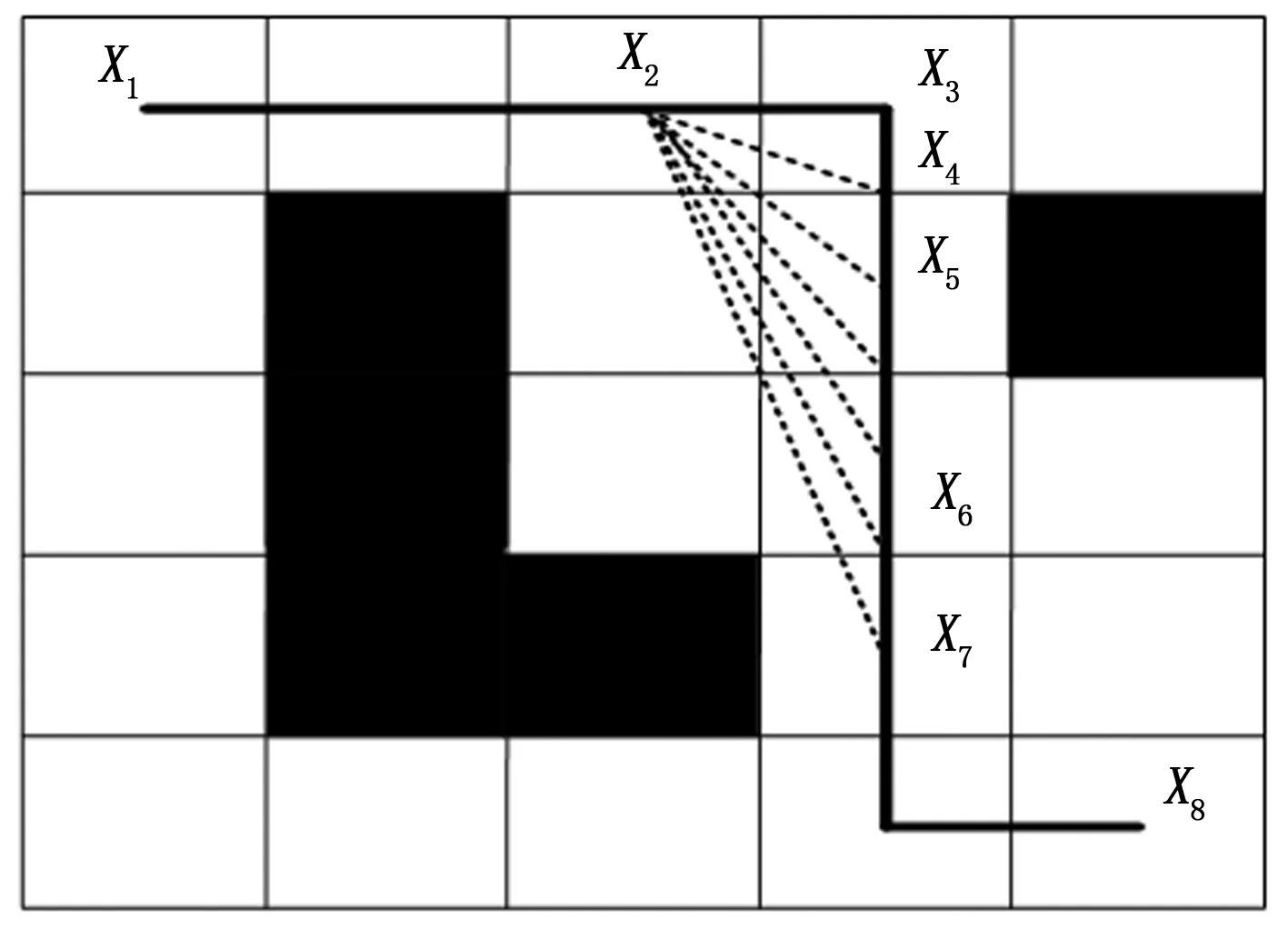
图2 剔除冗余节点示意图

图中黑色部分表示障碍物，白色部分为可通行空白区域，黑实线表示未经优化的路径，X1到X8代表路径上的不同节点，虚线表示的是机器人可经过的路径。以X2节点为例，按照节点优化策略，X2节点跳过相邻节点，连接至X4，比较X2X4之间是否经过障碍物，即机器人能否顺利通过，若可以经过，再检查距离和之前相比是否变短，路径确实变短后，检测能否被机器人执行，能否执行主要查看24扩展邻域搜索范围，若在24扩展邻域范围内，则可以顺利进行节点优化并将该路径加入到候选表中。检查完X4节点，我们继续检查X5节点，重复上述流程，若X5也符合上述检测标准，则将X4和X5两个节点进行对比，由分析可知，X2X5路线所优化的路程长度大于X2X4，因此将X5替换掉候选表中的X4。由于机器人搜索区域的限制(24邻域)，上图中最佳的路线为X2X6。从头到尾重复上述流程，最后将选出一条更为平滑的路径。

1.5 改进A*算法实验结果

本文选用60*60的栅格对A*算法和改进A*算法分别进行仿真验证，实验结果如下图所示。

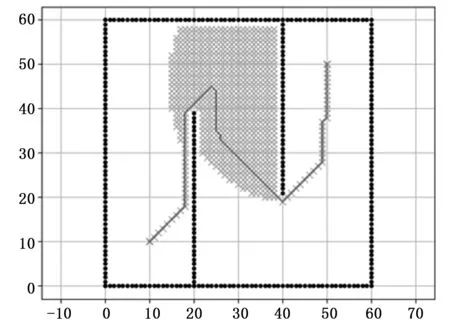
图3 原始A*算法

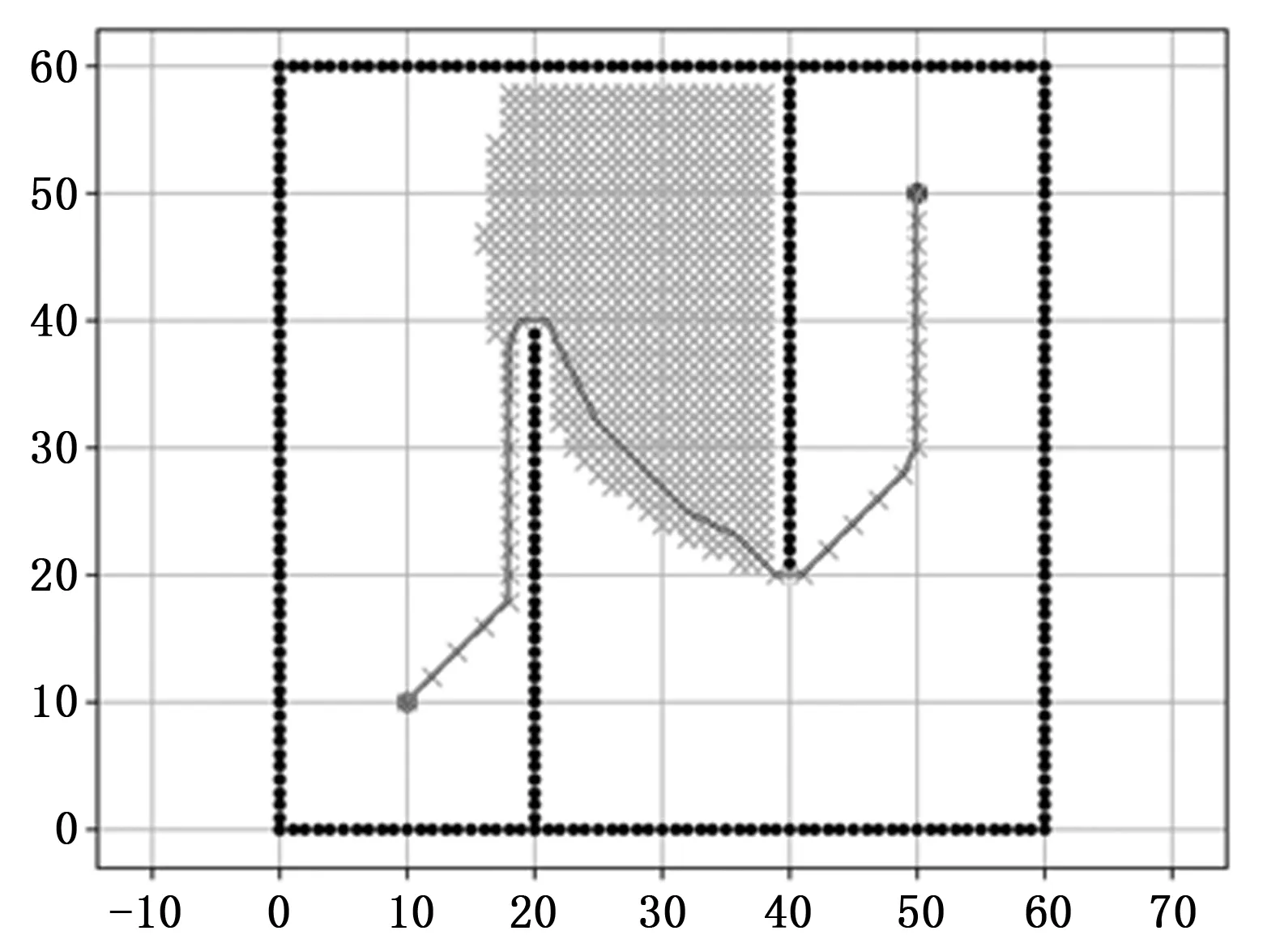
图4 改进A*算法

图中位于坐标(10,10)处的红点为机器人起始点，位于坐标(50,50)处的点为机器人要到达的目标点，实心点表示的是障碍物，白色区域为空白地带，浅色区域为算法搜索过的点，曲线表示最终规划出的去全局路径。由上述两个图可以直观的看出，改进后的A*算法能够以更少的代价到达目标点，而且轨迹更加平滑，更加理想。

2 动态窗口法

动态窗口法的基本思路是：在速度空间中，根据自身运动模型，对多组速度进行采样，分析出在各组不同速度下，一段时间内机器人的运动轨迹，采用一定的评价函数对该组轨迹进行评价，选择出评价最高的一组来执行，直到下一执行时间的到来。动态窗口法示意图如图5所示。

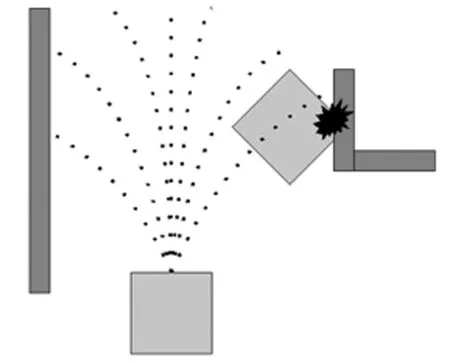
图5 动态窗口法示意图

如图5所示，矩形表示机器人，物体表示障碍物，虚线表示的是动态窗口法规划出来的下一时刻内的多组轨迹，由图可知，有三组轨迹将碰到障碍物，因此将这三条轨迹舍弃，然后将剩下的轨迹通过其他评价函数进行评分，最终选择出最适合的一条轨迹执行。

2.1 机器人运动模型

在动态窗口法中，对机器人建立运动模型是最基本的步骤。

假设机器人在间隔时间内沿着直线运动。若机器人是非完整约束的，即不能进行全向移动，只能进行前进和旋转。我们先计算机器人在相邻时刻的轨迹。 假设机器人在该相邻时刻之间是匀速运动的，由于相邻时间间隔很短，我们将其进行近似处理成一段直线。此时可以得到机器人在世界坐标系中的位移：

Δx=υΔtcos(θt)

(6)

Δy=υΔtsin(θt)

(7)

由上述位移公式我们可以得到机器人在一段时间内的轨迹：

(8)

若机器人能够进行全向运动，我们需要另外将机器人在纵轴移动的距离投影到世界坐标系。此时我们推导：

(9)

一段相邻时间内假设机器人的轨迹是直线是不准确的，若要得到更精确的结果，我们需要将轨迹假设为曲线，最终轨迹是由许多段圆弧构成。假设机器人不能进行全向运动，那么轨迹中圆弧的半径为：

γ=υ/ω

(10)

机器人坐标为：

(11)

为了使最后结果更加精确，本文使用的是第二种模型，即假设机器人在相邻时间内的轨迹是圆弧。

2.2 机器人速度采样

得到了机器人运动模型之后，下一步就是确定机器人的速度，这一步是动态窗口法的核心，只有得到了机器人速度才能对机器人的轨迹进行预测。在速度空间内，机器人可以在当前时刻理论上可以由无穷多组，但是由于各种条件限制，可以将速度限制在某些范围内。

机器人受到自身极限速度限制：

Vm={υ∈[υmin,υmax],ω∈[ωmin,ωmax]}

(12)

机器人受到电机性能制约：由于不同电机具有不同的性能，提供给机器人的最大加减速也不一样，因此在一个动态窗口内显示的速度就是机器人能够实际达到的速度，设υc和ωc分别为机器人当前速度和角速度，可得机器人在电机性能约束下的速度范围：

(13)

机器人受障碍物约束：进行局部轨迹规划最重要的一点就是让机器人能够避开障碍物，动态窗口法刚开始并不知道障碍物的位置，在进行速度的不断选择和轨迹评价后，若有轨迹碰到障碍物，此时就可以计算出机器人到障碍物的距离，然后根据当前机器人本身性能，看是否可以以最大减速度在障碍物之前停下，如果计算出无法在障碍物之前停下，则将该轨迹删除。该条件下速度范围可以由下面的公式来进行约束：

(14)

2.3 评价函数

动态窗口法最后一步就是对预测的轨迹进行评价，我们采用三个不同的方面共同对轨迹进行评价，客观的得到最优路径。

第一个评价函数的方位角评价函数，方位角指的是机器人到达规划出的轨迹末端时，当前朝向和目标点朝向的角度差。在这里用180°-θ来表示，即角度差越小，评价函数值越大，接受程度越高，方位角示意图如图6所示。

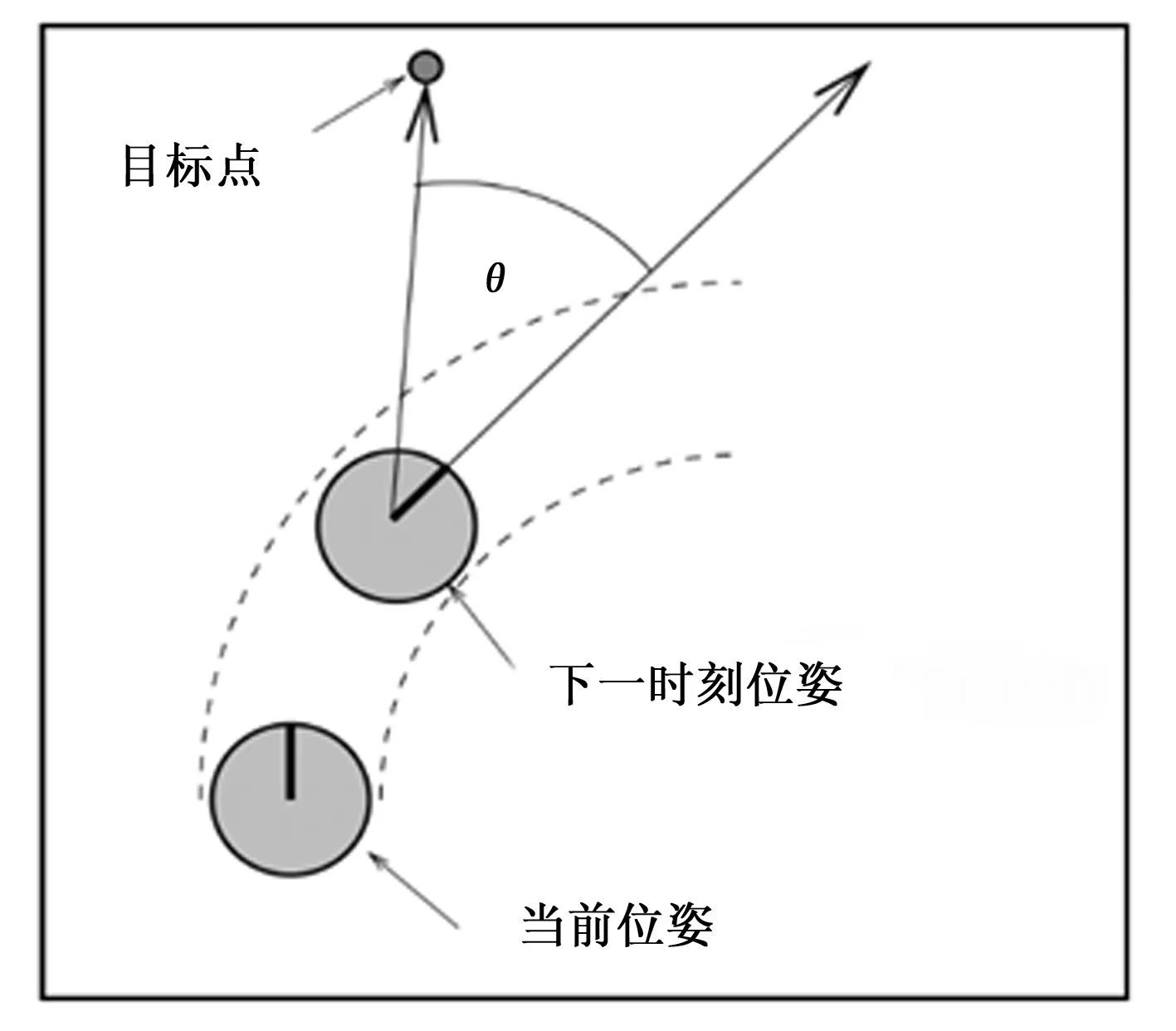
图6 动态窗口法方位角示意图

第二个评价函数为距离评价函数，也就是轨迹末端距离障碍物的远近程度，若轨迹与障碍物相交，则将次轨迹舍弃， 将其设定为一个常数。

第三个评价函数为速度评价函数，用来评价当前机器人速度大小，速度间接影响到机器人距离函数。

由上述三个评价函数得到的总评价函数为：

G(υ,ω)=σ(α·heading(υ,ω)+β·

dist(υ,ω)+γ·velocity(υ,ω))

(14)

上述公式中heading(υ,ω)，dist(υ,ω)，velocity(υ,ω)分别表示机器人的方位角评价函数，距离评价函数和速度评价函数。为了使轨迹更加平滑，要对评价函数进行归一化处理，以方位角评价函数为例，归一化指的就是每一项除以每一项的总和：

(15)

同理，其他两个评价函数也可用相同方法进行归一化平滑处理。

2.4 动态窗口法验证

如图7所示，为了验证动态窗口法的性能，我们对该算法进行仿真验证，机器人需要绕过障碍物到达目标点。一连串线条表示动态窗口法所评价的轨迹，在这些轨迹中选择一条最优轨迹执行。

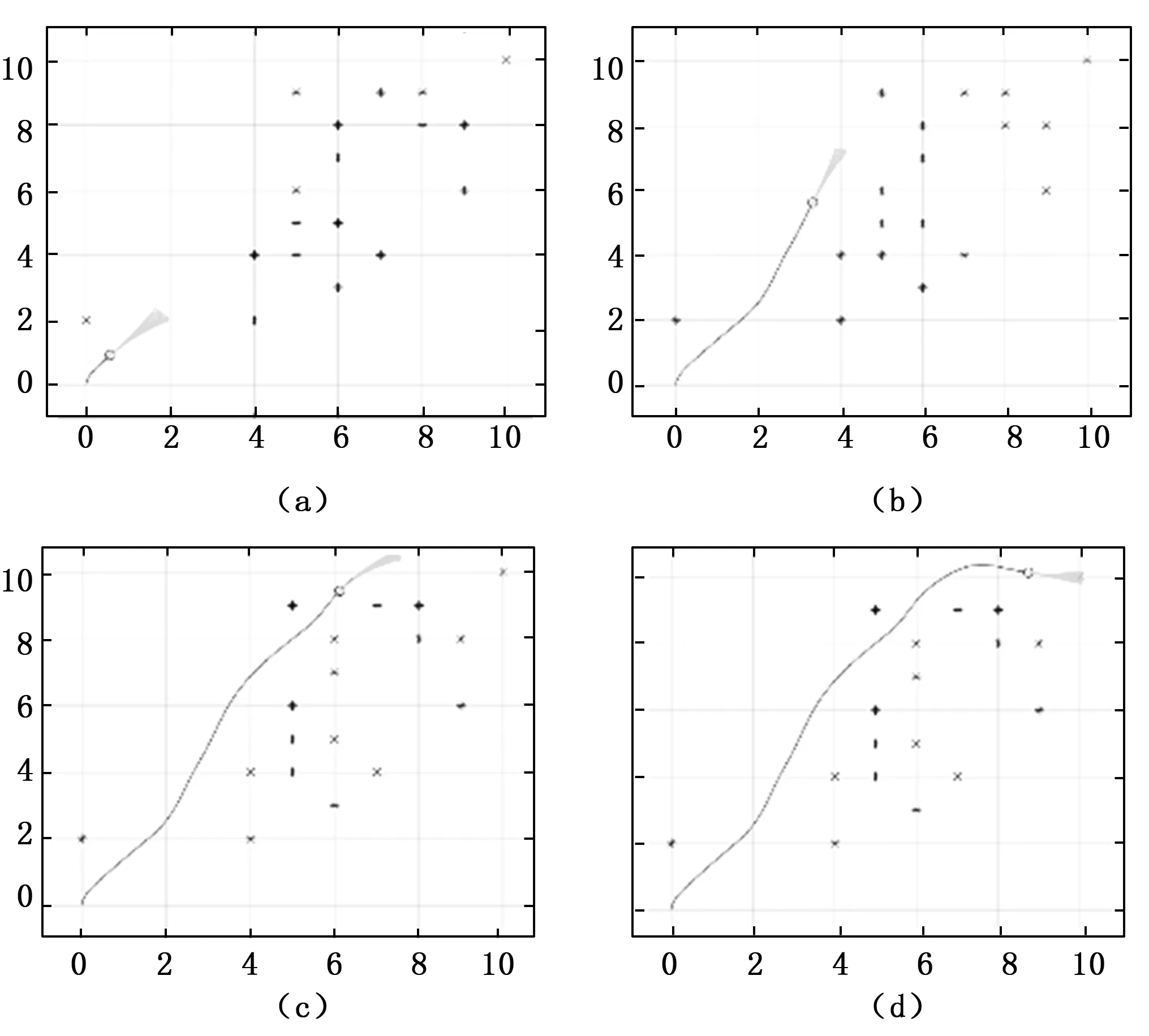
图7 动态窗口法的MATLAB仿真结果

3 系统综合实验

3.1 实验仿真平台介绍

本文仿真采用的是Ubuntu系统下的机器人操作系统(ROS，Robotic Operating System)，该操作系统于2007年诞生于斯坦福大学人工智能实验室，虽然被称为操作系统，但它只是借鉴了操作系统的精华，提供给用户一系列方便的服务。作为一个开源操作系统，ROS为广大研发人员提供了大量接口，支持多种编程语言，模块化编程，大大提高开发效率。

ROS还为我们提供了大量软件接口，例如广泛使用的Gazebo物理仿真平台，Rviz数据可视化工具等，我们可以用这些工具很方便的进行开发。

3.2 实验结果

本实验在Gazebo平台下搭建了轮式机器人以及具体的3D仿真环境，同主题将Gazebo与Rviz连接起来，这样我们就可以将机器人在仿真环境中将具体的机器人采集到的数据进行直观展示。物理仿真结果如图8所示。

图8 Gazebo物理仿真环境搭建

在Rviz中设定机器人初始点和目标点，橙色曲线表示为改进A*算法规划出的全局路径，红色箭头表示设定的机器人最终位姿，机器人前方一系列绿色箭头指的就是利用动态窗口法计算出的诸多预测轨迹，在其中找到最优的一条执行。为验证机器人避障性能，设置机器人最大线速度为2 m/s,最大线加速度为0.8 m/s2,评价函数参数α=0.1，β=0.3，γ=0.2。从仿真结果可以看出机器人能够很顺利的从初始点沿着全局路径前进，并按照自身机械结构限制进行路径的改良。

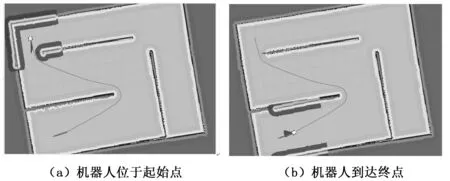
图9 Rviz数据可视化结果

通过统计仿真过程中路径节点，运行时间等数据，我们可以更加直观的看出改进A*算法和传统A*算法之间的差别，统计表如表1所示。

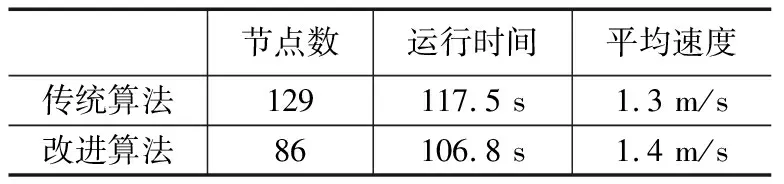
表1 两种算法对比

从表中可以看出，改进后的A*算法搜索的节点数目更少，轨迹也更短，直接导致效率的增加，机器人行动速度变快。

4 结论

本文针对移动机器人路径规划，提出一种改进A*算法，将算法搜索区域扩展到24邻域，克服传统A*算法路径转折点多，不够平滑，不易被机器人执行的缺点，并设计了一种节点优化策略，遍历规划好的路径节点，剔除冗余节点，使路径更优。最后加入动态窗口法，极大提高了机器人避障能力，在保证路径全局最优的同时，可使机器人平滑的到达目标点。

本文设计的改进A*算法在小型地图上效果显著，但是在大规模地图中，由于计算量过大，导致机器人实时性能低下，效果不如传统算法，需要进行进一步优化。