一种改进的基于压缩感知的心电压缩算法
, ,,
(1.中国科学院微电子研究所,北京 100029; 2.江苏物联网研究发展中心,江苏 无锡 214028;3.中国科学院大学,北京 100864; 4.新一代通信射频芯片技术北京市重点实验室,北京 100029)
0 引言
心血管疾病正严重威胁人类身体健康,根据世界卫生组织统计:在2015年全球范围内的死亡病例中,有31%死于心血管疾病[1]。由于缺乏明确的预警信息,很多心血管患者在到达医院之前就已经失去生命体征。如果有适当的治疗和紧急护理,这种病例的发生频率将大大降低[2]。
动态心电监测技术可以在不影响病人正常生活的情况下,长时间地对其心脏进行实时监测,从而能够发现心脏的异常活动、隐性威胁。目前,动态心电监测已经成为心电监测新的发展趋势之一[3]。动态心电监测必然会产生大量数据,目前主流的远程动态心电记录仪采样率能达到1 000 Hz、分辨率高达24位[4]。若在8通道下对病人心脏24小时不间断检测的采样数据大约为1.93 GB,可见心电数据压缩对于动态心电记录仪是必不可少,如果将采集到的心电数据先进行压缩再传输,可以降低传输功耗,还可减少所需存储空间。
压缩感知(CS,compression sensing)的提出解决了传统奈奎斯特采样技术的高能量损失问题[5]。 将CS引入心电压缩后,可以通过减少对存储空间、数据吞吐量和信道传输带宽的需求。然而,与最先进的有损压缩算法相比,它的压缩比是有限的。直接差分位压缩算法是一种无损压缩算法[6],不会影响基于CS算法的重构精度,为了充分利用二进制表示,对大数移位进行操作,将该算法命名为移位差分位压缩算法(SDCA, shift difference bit compression algorithm)。将基于压缩感知理论的压缩与移位差分位压缩结合的算法称为CS-SDCA。 CS-SDCA的压缩比等于CS算法的压缩比乘以SDCA的压缩比,大大提高了压缩比,降低了采集前端的能耗。
1 系统结构及原理
1.1 系统结构
图1给出了远程动态心电记录仪的基本结构,它也是实验的主要数据来源。记录仪由心电采集前端、数据传输网和后端解压模块组成。由于数字采集系统根据奈奎斯特-香农采样率通过模数转换器完成心电数据的采集,所采集的信号具有离散样本。然后压缩模块采用压缩算法在嵌入式操作系统或单片机中对心电信号进行压缩。压缩后的心电信号通过蓝牙传输到远程解压缩端。解压缩端将暂时存放压缩后的心电数据,若需要心电数据时,通过解压缩算法获得重构心电信号。
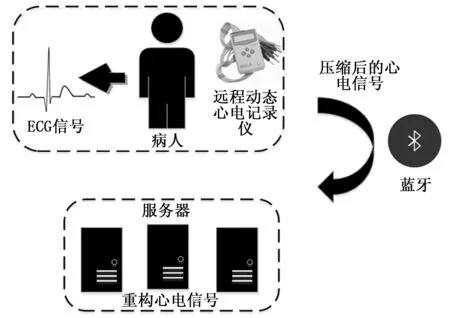
图1 远程动态心电监测系统
1.2 压缩和重构算法
图2给出了心电数据压缩和重构算法的流程图,其中包括心电信号预处理模块、心电信号压缩模块和重建模块。在模数转换后通过滤波网络对心电数据进行滤波。滤波模块滤除运行噪声、工频噪声、呼吸波噪声、人体噪声等噪声干扰信号。使用所提出的算法对数据进行压缩,然后传输。最后,压缩后的心电数据在服务器端重建。在采集的前端,压缩算法需要计算并且可集成到芯片上,所以需要关注压缩算法的功耗问题。解压缩端具有强大的数据计算能力,因此只需要考虑信号重构的准确性,而不必特别注意重构算法的计算复杂度。
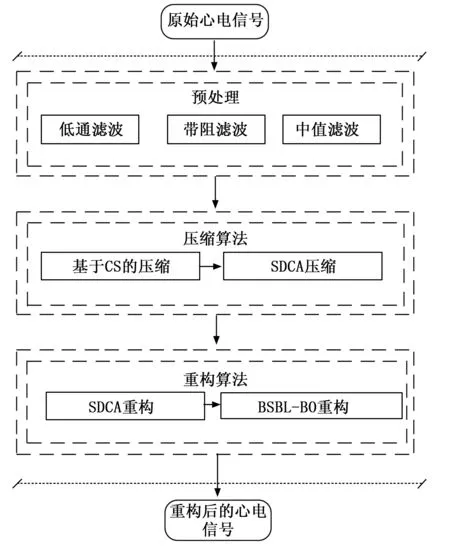
图2 压缩算法流程图
1.2.1 预处理
很多有关心电信号压缩重构的研究并未提到原始信号的预处理,仅在重构过程中估计了噪声的分布,而通过仿真发现针对心电信号的特点对其进行相应的滤波处理后,可以提高重构算法的精度。考虑到重构精度的需求,意味着该滤波模块不能影响心电信号的空间结构信息和时序结构信息。
滤波模块加入了低通滤波器、带陷滤波器、中值滤波器,它们用于滤除心电信号中主要噪声。其中低通滤波器采用截止频率为75 Hz的巴特沃斯滤波器来滤除肌电干扰;带阻滤波器采用上限频率为51 Hz、下限频率为49 Hz的巴特沃斯滤波器来滤除工频干扰;中值滤波器用于纠正呼吸产生的漂移。
1.2.2 CS和BSBL-BO
CS是一种新的信号压缩方法,它依赖于信号的稀疏性来压缩和重构。基本的噪声模型可以表示为[7]:
Y=ΦX+V
(1)
式(1)中X∈RN×1,Φ∈RM×N;感知矩阵Φ的列之间线性无关;V是在压缩过程中产生的噪声向量。
心电信号在时域是非稀疏的信号,很多压缩算法只考虑重构心电数据中远非零的数据,但是一些接近于零的值往往是一些疾病的重要诊断指标。这要求重构算法能以极高质量重构出心电信号,目前仅有基于边界优化的块稀疏贝叶斯模型(block sparse bayesian learning,BSBL-BO)重构算法[8]能做到这一点。
自然界信号广泛具有的结构是块结构,具有这种结构的信号被视为多个块的级联,例如:
(2)
基于这个块划分的压缩感知模型称为块稀疏模型。在块稀疏 CS 模型中,假设每γi个块xi都满足多元高斯分布,且其中每块相互独立[9]:
p(xi;γi,Bi)~N(0,γiBi)
(3)
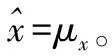
(4)

1.2.3 SDCA
为了进一步提高压缩比,降低传输压力,本文提出一种简单有效的自适应无失真编码算法。根据心电数据分辨率不同,算法自动选用不同码长的差分位压缩编码算法,相比于哈夫曼码的不等长编码给存储带来的不变,该编码算法简单、运算量小,非常适合于前端电路的实时实现。
心电数据经过式(1)的运算后得到初步压缩后的数据Y,感知矩阵为0/1简单矩阵。利用式(5),得到差分量H,位压缩即对此量进行重新编码传输,其中n根据不同的分辨率取不同的值,取2的整数次幂,用右移运算代替除法操作。
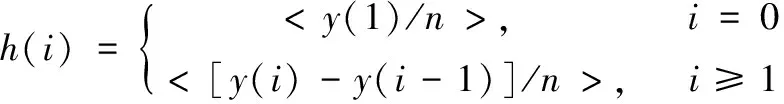
(5)
若选用a-b-c差分压缩编码,即采用a/b/c位长度分别表示相应的差分值,其中b位中包含a个1作为标志段,c包含b个1作为标志段。令α=2α-1,β=2b-1,μ=2c-1。
直接差分位压缩会导致某些二进制表达没有被用到,b位长的二进制表达数据不包括a位长二进制表示过的数据,即该算法中未使用b位长二进制表示的一部分。c位长度二进制数也是如此。因此,如式(6)所示,通过对h(i)进行移位操作来进一步改进算法,得到Hs,将Hs传输到解压缩端。

(6)
移位差分位压缩的基本原理是将心电信号差值编码为可对应的码长,根据不同的分辨率选择不同的编码方式,只需要保存差值Δy(n)、y(0),就能重构出原始信号Y。a/b/c三种位长的方式也可以是两种位长或者四种位长,根据数据分布不同具体而定。对编码后数据的解码过程即是编码算法的逆运算。
2 实验结果
本文将MIT-BIH心律失常数据库中48 组心电信号、MPS450心电模拟仪模拟不同心率的数据以及人体实测数据作为训练数据集作为实验数据集。为了与本文中的设备以1 000 Hz采样率采集心电信号的特征符合,对采样率为360 Hz的心电信号重采样为1 000 Hz的心电信号,即将原本一个通道650 000个点的数据重采样为1 805 554个点。
为了量化压缩性能,同时评估心电信号的重构质量,本文采用了最广泛使用的性能指标,即压缩比和百分比均方根差(PRD)[10]。 CR的定义是:
(7)
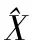
(8)
PRD<9%的重构信号可用于医学诊断。
2.1 MIT-BIH 心率失常数据库
2.1.1 SDCA实验结果
经过CS算法后得到的初步压缩数据Y,利用式(5)、(6)得到待压缩量Hs,其中n=8。当心电信号的分辨率为12位时,有三种编码算法备选,分别是4-8-12、2-4-8-12和8-12差分压缩编码。
4-8-12差分压缩编码的压缩比更优,96包数据的平均压缩比为1.648 5。基于2-4-8-12差分压缩编码、8-12差分压缩编码的平均压缩比分别为1.515、1.48。综上在对MIT-BIH数据库位压缩算法选择4-8-12差分压缩算法,即在分辨率为12位的时候采用SDCA4-8-12的移位差分位压缩算法。8位长的二进制需要添加1 111作为标志,12位长的二进制添加111 111 111 111作为标志。
表1给出了MIT-BIH数据库中直接差分压缩算法和移位差分压缩算法的压缩比。直接压缩算法包括[-7,7]、[-127,127]、[-2 047,2 047]区间。SDCA包括[-7, 7], [-134,135], [-2 181, 2 183]区间。 可以看出,SDCA的压缩比比直接压缩算法高约1%。由于心电信号被CS压缩后再通过SDCA压缩,差分压缩对压缩比的影响会更加明显。
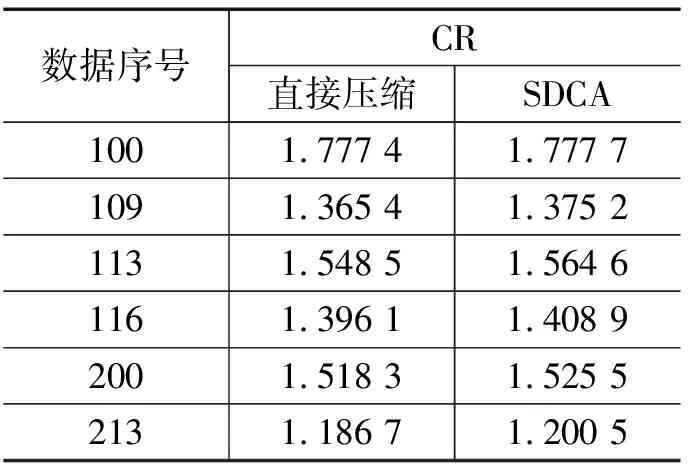
表1 一阶差分值统计结果
SDCA 4.8.12的解码过程是编码过程的反过程,其它不同位数的位压缩算法原理与此相似。位压缩属于无损压缩,所以经过该算法在没有任何损失的情况下提供了1.648 5左右的压缩比。
2.1.2 BSBL-BO 算法实验结果
本文采用离散余弦变换对心电信号进行稀疏变换。本文中感知矩阵的非零量d取1,矩阵维度为,每列选取随机15个位置设为1,其他位置均为0,并以20个点长均匀分块重构。在这个基础上此压缩阶段仅做加减运算大大节约了采集前端功耗,编码过程采用滑动窗口的方法分段编码ECG,每段250个点可以等分每秒采集的1 000个点,方便了算法对心电信号的分块处理。
如图3所示,算法对压缩后心电信号的重构效果非常好,PRD值均远远低于9%,可用于心电专家的后期诊断。
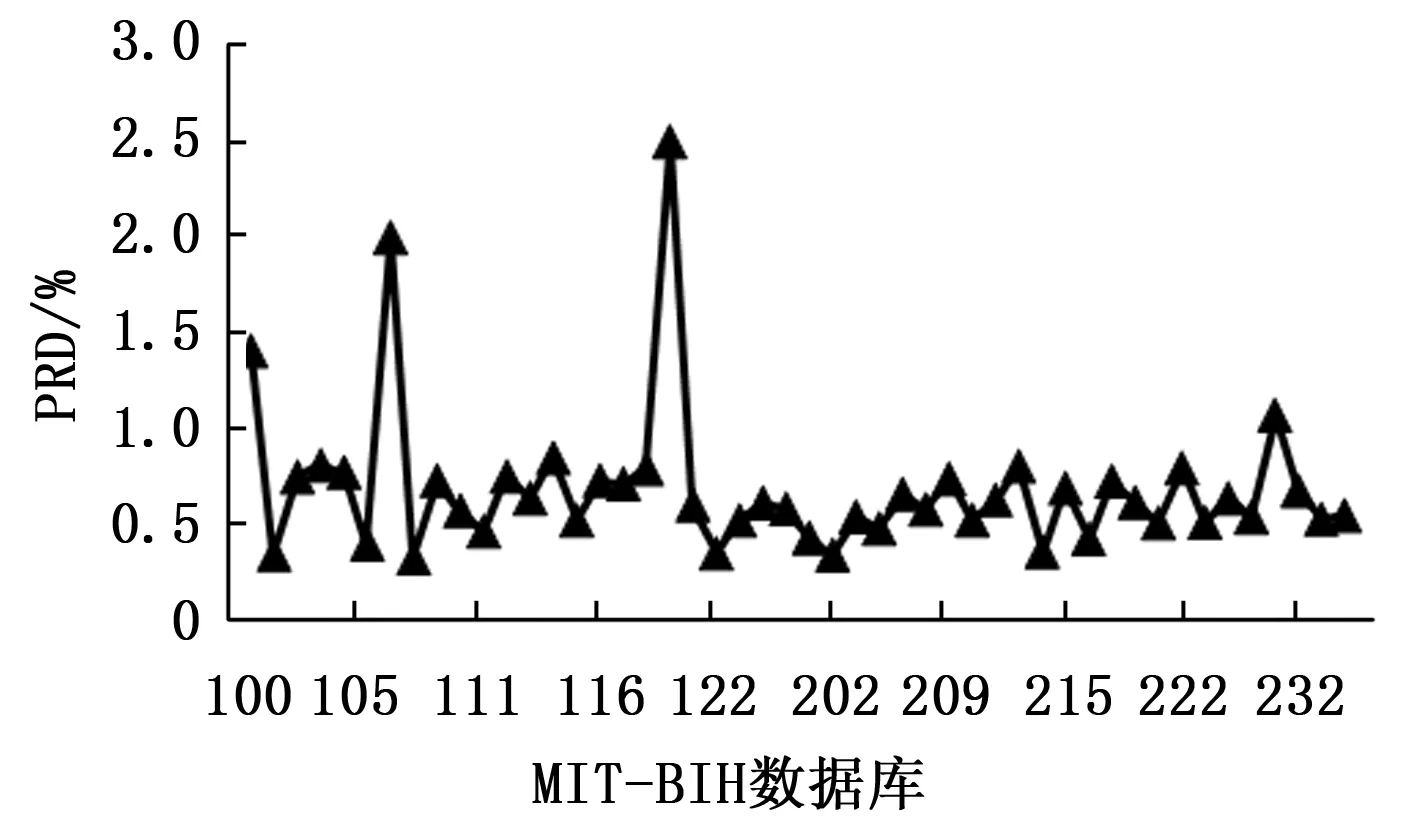
图3 BSBL-BO在MIT-BIH数据库的PRD
2.2 远程动态心电记录仪采集数据
利用图1的动态心电记录仪采集实际数据,该心电记录仪采样率为1000 Hz,分辨率为24位,一次性采集8小时病人心电信号,分别在一个月内对该病人每隔5天采集了6组数据。采集时间是在病人夜间睡眠期间,环境是病人家内,该病人73岁,性别男,做过心脏搭桥手术,有心肌缺血症状。采集得到前两分钟的心电数据由于设备稳定问题已舍弃。当分辨率为24位时,n取128,使用SDCA8.12.16.24算法。
表2给出了心电模拟仪模拟不同心率心电信号的位压缩压缩比,CR平均值为2.36。CS-SDCA压缩算法得到的压缩比随着心率的增加有所降低,但仍然满足设备需求。此外,采用SDCA8.12.16.24对远程动态心电记录仪连续8小时间实际采集的心电数据压缩,平均压缩比为1.97。

表2 SDCA8.12.16.24的压缩比
对不同HR的心电信号重构的PRD值均小于9%,均可满足后期心电医师诊断的需求。另外远程动态心电记录仪采集的数据平均PRD为4.811 9%。也就是说本文设计的算法对实际采集数据的压缩重构效果很好。
3 讨论
3.1 CS-SDCA 压缩比
论文中采用两种压缩算法结合的方法,提高了系统压缩比。压缩感知的压缩算法感知矩阵维度固定为,也就是说,当再提高这部分的压缩比时会导致重构效果变差。信号的重构质量是优先于压缩倍数考虑的,所以本文令感知矩阵维度为,以保证重构质量。移位差分位压缩的压缩比不固定,在本文的测试数据中最大压缩比为2.824 6,此时系统的,最小值为1.07,系统压缩比为4.18。
本文比较了CS-SDCA与BSBL-BO,BSBL-FM[11]和SDCA的功耗和重构精度,实验数据为 MIT-BIH心律失常数据库,重复20次实验求平均。算法测试阶段仿真条件均是MATLAB 2013A,Intel Core i7-6700 CPU,4 GB RAM。结果如图4,在实验中感知矩阵均是维度,可以看出在相同压缩比的前提下BSBL-BO算法比BSBL-FM算法重构效果好很多,而解压缩部分是在服务器端完成,运算能力较强,所以BSBL-BO更适合本文算法,由图也可看出SDCA算法运算速度很快,所以CS-SDCA算法在提高了压缩比的同时没有过多的增加功耗。
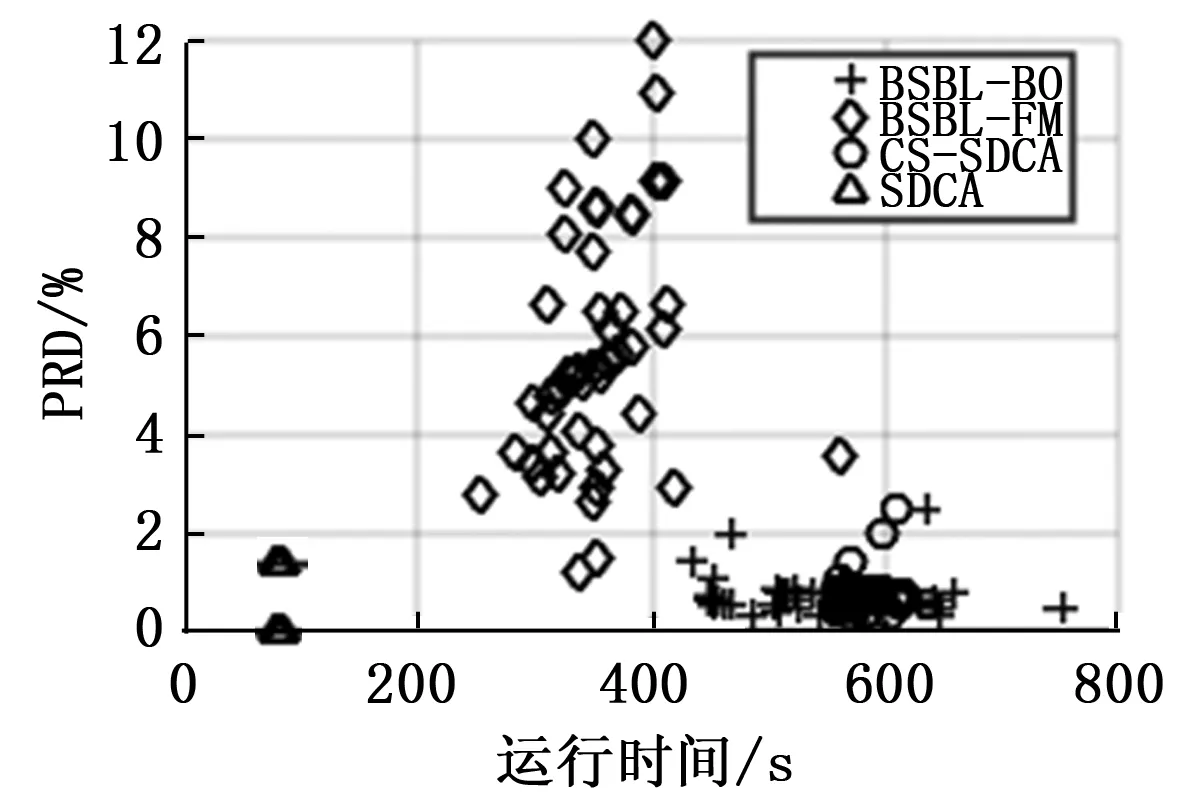
图4 不同算法平均PRD和CPU运行时间对比
综上所述,CS算法保证了近四倍的压缩比,SDCA算法进一步提高了系统压缩比。
3.2 CS-SDCA功耗
本文针对远程动态心电记录仪设计了心电压缩算法,从计算复杂度角度考虑,压缩端包括CS和SDCA算法两个模块。例如,当压缩250个点的信号时,使用感知矩阵仅需要1024个加法,其中感知矩阵中每列随机有16个1, 若对功耗还有进一步的减低,可以减少感知矩阵中1的个数。对于移位压缩算法250个点需要250次加法,大约500次以4字节为单位的移位操作,即算法对每块250个数据一共需要1 274个加法和500次移位操作,编码端计算复杂度为O(N)。
动态心电记录仪采用nRF51822低功耗蓝牙芯片,工作电压3.3 V,工作电流为0.6 mA,完整工作电流为2.5 mA,蓝牙传输占了系统功耗的76%,所以减少数据量继而降低蓝牙传输功耗对整个动态心电记录仪降低功耗具有十分显著的效果。以压缩算法O(N)的计算代价,当只经过CS压缩时大约减轻了蓝牙传输50%的功耗,随着压缩比的提高,会更进一步降低系统功耗,延长设备使用寿命。
4 结束语
数据量庞大是远程动态心电记录仪的难点所在,而压缩感知的压缩算法压缩比有限,本文是针对该问题所设计的心电信号压缩重构算法,将无损压缩算法移位差分位压缩算法与压缩感知结合,将压缩倍数提高的同时,保证了心电重构质量满足后期医师诊断的需求。虽然本文提出的算法应用于远程动态心电记录仪,但因为算法压缩端功耗极低,也可应用到无线体域网中。

