基于层次覆盖的多层网络社团发现算法

, ，，

(西安理工大学 自动化与信息工程学院， 西安 710048)

0 引言

现实世界中的许多复杂系统可以用复杂网络来表示，社团结构是复杂网络的一个重要拓扑特性[1]，它具有同一类节点之间联系紧密，不同类节点之间联系稀疏的特性。社团发现是根据复杂网络里隐含的拓扑信息来找出其中的社团结构，它可应用于信息标签化、预防病毒，预测行为等。研究复杂网络社团结构的性质不仅有助于分析复杂网络的功能，对研究生物学、医学、工程学、计算机科学等也具有十分重要的意义。因此，对社团发现算法的研究受到了国内外许多学者的广泛关注[2]。

目前，已经存在的社团发现算法多针对于单层网络，例如：以图分割[4]、GN[5]算法和标签传播算法(LPA)[6]为代表的从网络的整体到局部的社团发现算法，当然也有以Newman快速算法[7]、谱聚类[8]算法和CNM[9]算法为代表的从网络的局部到整体的社团发现算法。对多层网络的研究最初起源于社会科学领域，后来发展到医学、计算机科学等。近年来，多层网络的研究逐步发展起来，继而出现了许多多层社团发现算法：CLEDCC算法[10]、多层α-核散列聚类的异常数据社团发现算法[11]、基于多层粒子群的社团发现算法[12]、CLECC算法[13]、多层网络局部社团发现算法[14]以及通过比较节点度之间的关系来发现多层网络中的局部社团结构[15]等。

为了提高目前多层网络社团发现算法社团划分的准确度，以及对于一些没有直接相连的节点作出准确的划分。本文提出一种新的算法，通过结合RA相似度提取拓扑信息，从而间接的提取社团结构。这种基于层次覆盖的多层网络社团发现算法在时间复杂度方面得到了改善。实验结果表明，该算法能较准确地划分出多层网络中的社团结构，避免了对多层网络划分的局部性。

1 算法

1.1 多层网络

定义单层网络G=，其中节点集为V=(v1,v2,...,vn)，n是节点数目，边集为E，(vi,vj)表示节点i与j之间的边。图1是一个简单的无权无向图，假设它是某实验室的成员图，每个节点代表一个成员，每个边代表成员之间的关系。

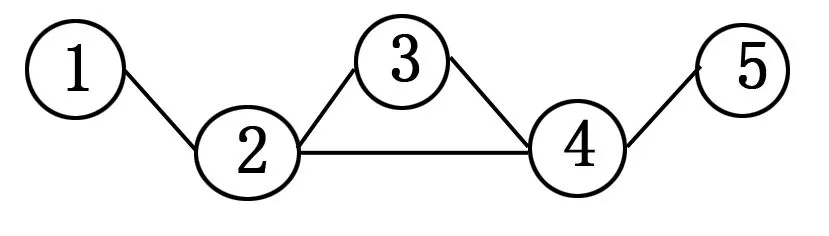
图1 单层网络模型

一个特定复杂系统构成一个单层网络，人们在生活中会碰到各种各样的单层网络，比如在日常通信中会用到的微信这一通讯工具，微信里的朋友圈就构成了一个单层的复杂系统。然而，随着社会的快速发展，人们在平时的社交过程中不仅仅局限于微信这一种通信工具，还会涉及到微博、E-mail、Twitter、Facebook等，每一种通讯工具都会构成一个单层的复杂系统，因此，日常生活中人们处在多个单层的复杂系统之间，这就构成了一个多层次复杂系统即多层网络。

多层网络的每一层都可以用一个图来表示，由于图与图的某些节点是相互对应的关系，且多层网络是由多个相互对应的关系组成的网络，因此了解每一个多层网络里不同图节点之间的对应关系很重要。下面给出多层网络的定义：多层网络是一个单层网络的集合，多层网络G=，每一层网络的层次序号=，i=，i∈1,...,l，Vi和Ei分别是第i层网络的节点集和边集.图2是一个柱形多层网络的模型，第一层与第二层之间的节点都是一一对应的。假设第一层是微信网络，第二层是微博网络，如果微信里的用户在微博里都有注册，那么在微博网络里这些用户之间的关系可以代表他们在微信网络里的关系，在这里需要注意每个用户的账户只能在他所在的层次登录，不能在其他层次登录。图3是一个较为复杂的普通多层网络，假设第一层是Twitter网络，第二层是Facebook网络，第一层的节点2是Twitter网络里的某用户，那么第一层的节点2对应的第二层的两个节点2是他在Facebook网络里注册的不同的账户，因此，不同节点不一定代表不同的用户，而是不同的账户。

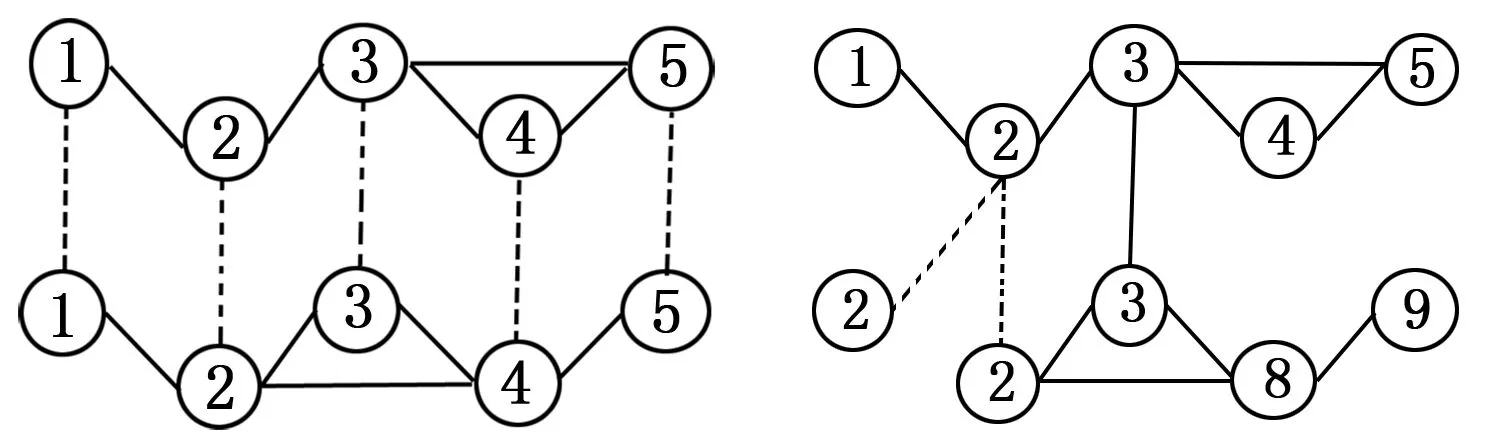
图2 柱形多层网络 图3 普通多层网络

1.2 RA相似度

由于多层网络的多重性，且为了准确的找到不同层次任意两个节点之间的连接密切关系，本文采用RA相似度[16]公式：

(1)

公式(1)中的φ(i)∩φ(j)表示节点i和节点j的共同邻居节点集合，k(i)表示两个节点共同邻居的节点的度.该相似度公式与以往的相似度公式不同之处在于：在比较两个节点之间的相似度时，已经存在的相似度公式仅考虑的是共同的邻居节点数目，如Jaccard相似度[17]，而RA相似度基于网络中资源配置的原理，通过比较两个节点之间的共同的邻居节点的特征来反映这两个节点之间的相似性。RA相似度通过公式(1)计算两个节点的共同邻居节点集合里每个节点的度，以得到两个节点之间的相似性。RA相似度的方法避免了局部相似度存在的一些问题，能更准确的比较两个节点之间的相似性，下面我们通过一个例子来介绍一下RA相似度公式：

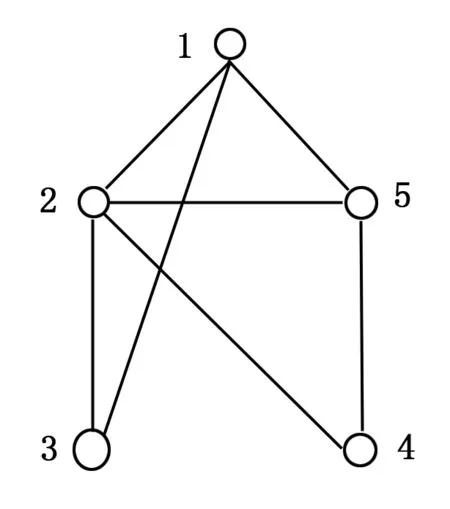
图4 节点图

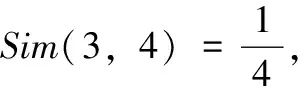
1.3 算法核心

给定一个多层网络G=，定义C为某一层的内部初始核心节点社团，定义D={v∈C|∃(u,v)∈E,u∈S}为社团C的边界子集合，定义S=(v∈VC|(u,v)∈E,u∈C)为外层节点集合，ED代表集合D与集合S中节点之间的边，是第i层的边集，定义L为局部社团相似性测度，表示为社团内部节点连接拓扑信息关系与社团间节点连接拓扑信息关系之间的比值。首先随机选取一个节点v作为初始社团C，通过比较给出两个公式来表示社团内连接关系和社团间连接关系：

(2)

(3)

公式(3)表示社团间节点连接拓扑信息关系。

1.4 判断条件

为了判断一个外层节点加入内部社团C后是否能加强社团的紧密性，定义局部社团相似性测度L来评价外层节点加入内层节点之后的效果，公式如下所示：

(4)

若外层节点u加入C后满足以下条件：

L(C∪{u})>L(C)

(5)

Lint(C∪{u})>Lint(C)

(6)

公式(5)、(6)表示若节点u加入社团C后，局部社团相似性测度L值变大，L值越大表明外层节点加入内层社团C后，C更紧密，且内层社团与外层社团连接更加稀疏，社团结构更加明显。且社团内部节点连接更紧密，此时将节点u加入到v所在的社团C中。在判断的过程中，每次将L取最大值时的外层节点加入到社团C中，迭代地判断每个节点，直到L不再增大。

用L作为划分节点的评判标准，将每次使得L值最大的外层节点划分到内层社团C中，直到不存在符合条件的节点出现为止，但这种方法在面对一些异常节点时通常不能有很好的划分效果，对于这种情况，若外层节点符合以下两个条件，就将它们划分到社团C中：

(7)

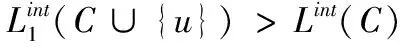
(8)

公式(7)表示加入节点u后，社团内连接系数较没加入u之前增大，社团间连接系数变小。明显地看出，公式(7)所述情况L值会增大，且符合(5)、(6)两个条件，此时，将节点u划分到社团C中。如果加入节点u后遇到公式(8)这种情况，即加入节点u后，社团内连接系数和社团间连接系数较之前都有增大，社团内部连接以及社团之间的连接都更加紧密，此时节点u有两种可能：

(1)节点u符合以上条件，且u不是核心节点，可以与社团C内的节点进行合并；

(2)节点u可能是一个核心节点，它与社团内和社团外的节点都有大量的连接。

对于(1)中的节点u，将它划分到社团C中。对于(2)中的节点u，暂时将它加入到C中，直到所有节点被划分到相应的社团后，再将这些疑似的核心节点从C中移除，此时，再返回到条件(5)、(6)对这些节点进行判断。

1.5 算法流程

该算法首先随机选取一个节点v作为覆盖第一层的中心节点，在初始阶段，集合D和集合C里只有节点v，集合S是外层节点集合，不断地从S集合里随机选出节点u，如果u加入到C中使得L值较大且能满足公式(4)以及公式(5)中的两个条件，则将u加入到v所在的集合里，迭代上述过程，在每一步迭代中，都要更新集合D、集合C和集合S，且直到L值不再增大，算法结束。具体算法流程如下所示。

算法：基于层次覆盖的多层网络社团发现算法：

输入：多层网络G；

输出：网络G的社团划分结果。

(1)初始化：随机选取一节点v加入集合C与集合D中，S为外层节点集合。

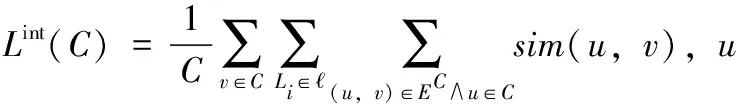
1)L(C∪{u})>L(C)加入节点u后，相似性测度L变大；

2)Lint(C∪{u})>Lint(C)加入节点u后，社团内部连接系数变大。

(4)若节点u同时满足条件1)和2)，将u加入到社团C中，若节点u为疑似核心节点，也将其放入C中，返回第(2)步，直到遍历所有节点，L不再变大，再将疑似的核心节点从C中移除，返回(3)对其进行重新判断。

(5)合并集合C与集合D,并计算不同层次的模块度Q。

2 实验分析

2.1 多层网络数据

为了测试算法的性能，会用到的不同的多层网络数据集，下面先来对这些数据集做一个简单的介绍。

MIT Reality Mining[18]网络数据集是通过给麻省理工学院87个移动用户安装一个软件，记录用户之间的数据交互信息，网络的每一层分别代表从现实中采集到的用户的物理位置、蓝牙交互和通话记录等用户之间的互动行为。

E-mail[19]网络数据集是一个记录Enron公司员工之间电子邮件往来的数据集，该网络有150个节点，每个节点代表1个用户，每条边代表2个用户之间发的一条电子邮件，该网络包括用户之间发送邮件的时间、发送主题、发送者账户以及接收者账户等。网络中的每一层分别代表员工之间的关系和邮件信息内容的相似性。

IMDB[20]网络数据集是一个互联网电影数据集，该数据集包含300个节点，每个节点代表一个一位演员，每条边代表这两个演员一起演了一部戏，该网络数据集的每一层分别代表第一年演员之间的合作、最后一年演员之间的合作、演员的平均收入和门票卖出的平均数量。

在实验仿真部分，用以上三个多层网络数据集对算法进行测试，测试了算法在三种网络上的运行时间，并用模块度Q[21]来评价社团划分结果，之后又将该算法与CLECC、CLEDCC两种算法进行了对比，结果表明本文算法的准确度更高，运行时间更少。

2.2 评价标准

为了评价社团划分的结果，采用Newman和Girvan提出的模块度Q。其定义式如下：

(9)

图5 随着层数的变化，社团数量的变化

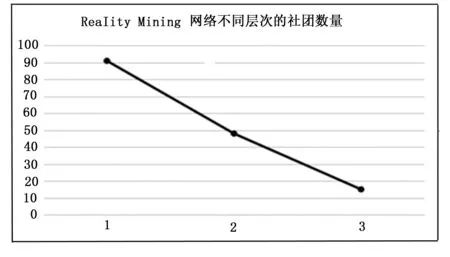
图6 随着层数的变化，社团数量的变化

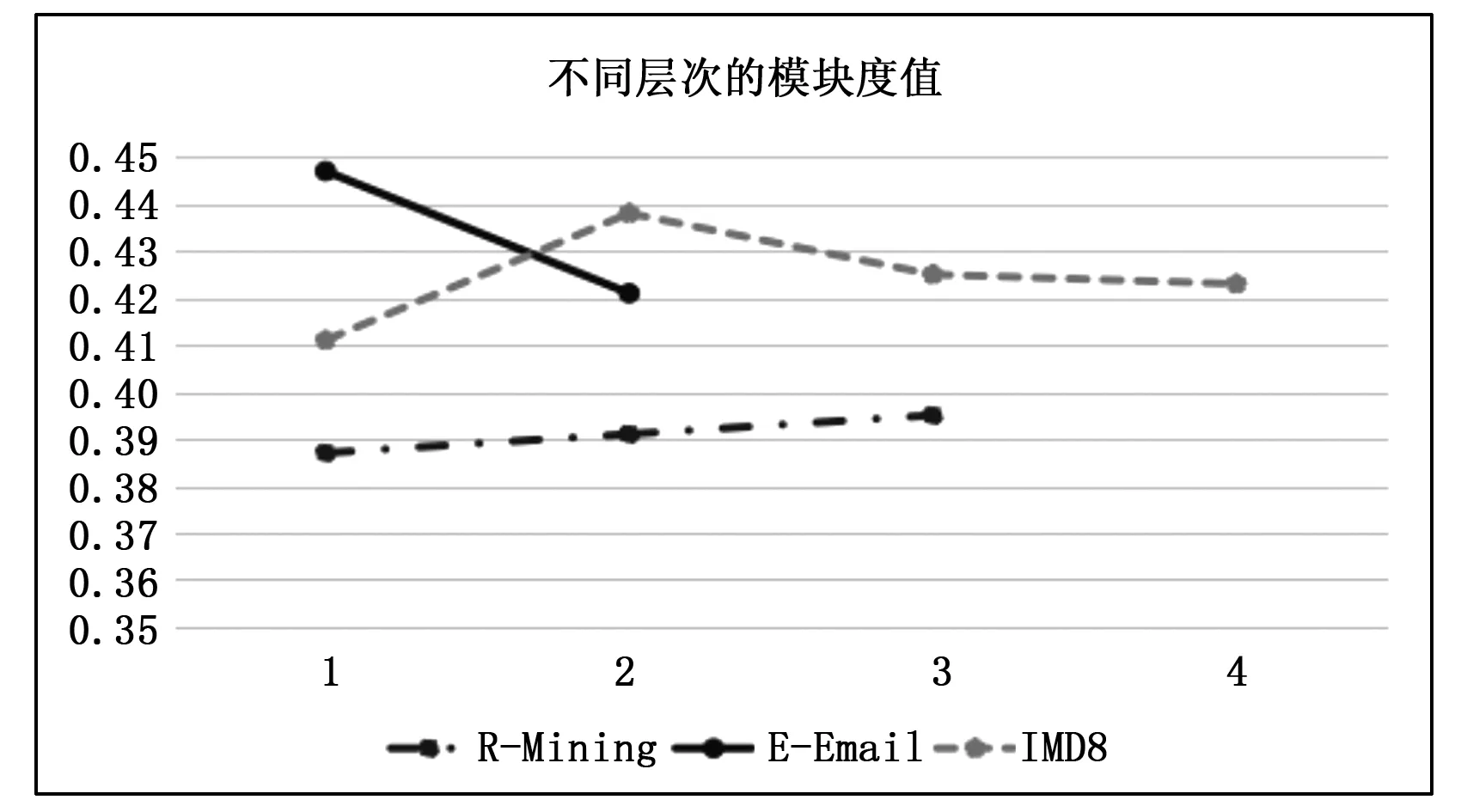
图7 不同层次的模块度Q值的变化

图5、6代表算法对三种网络的划分随着层数的变化，社团数量的变化，其中x轴代表某一层次，y轴代表社团数量。图7代表不同层次的模块度Q值的变化，其中x轴代表社团数量，y轴代表模块度Q值。

图8 E-mail网络模块度Q值对比

图8和图9分别是本文算法、CLECC算法以及CLEDCC算法在E-mail网络上以及IMDB网络上划分的模块度Q值的对比，其中x轴代表社团数量，y轴代表模块度Q值。从图8可以看出，将E-mail网络划分在24个社团左右时，有最大的模块度Q值，此时的划分效果较好。从图9可以看出，将IMDB网络划分在95个社团左右时，会得到较为明显划分结果。

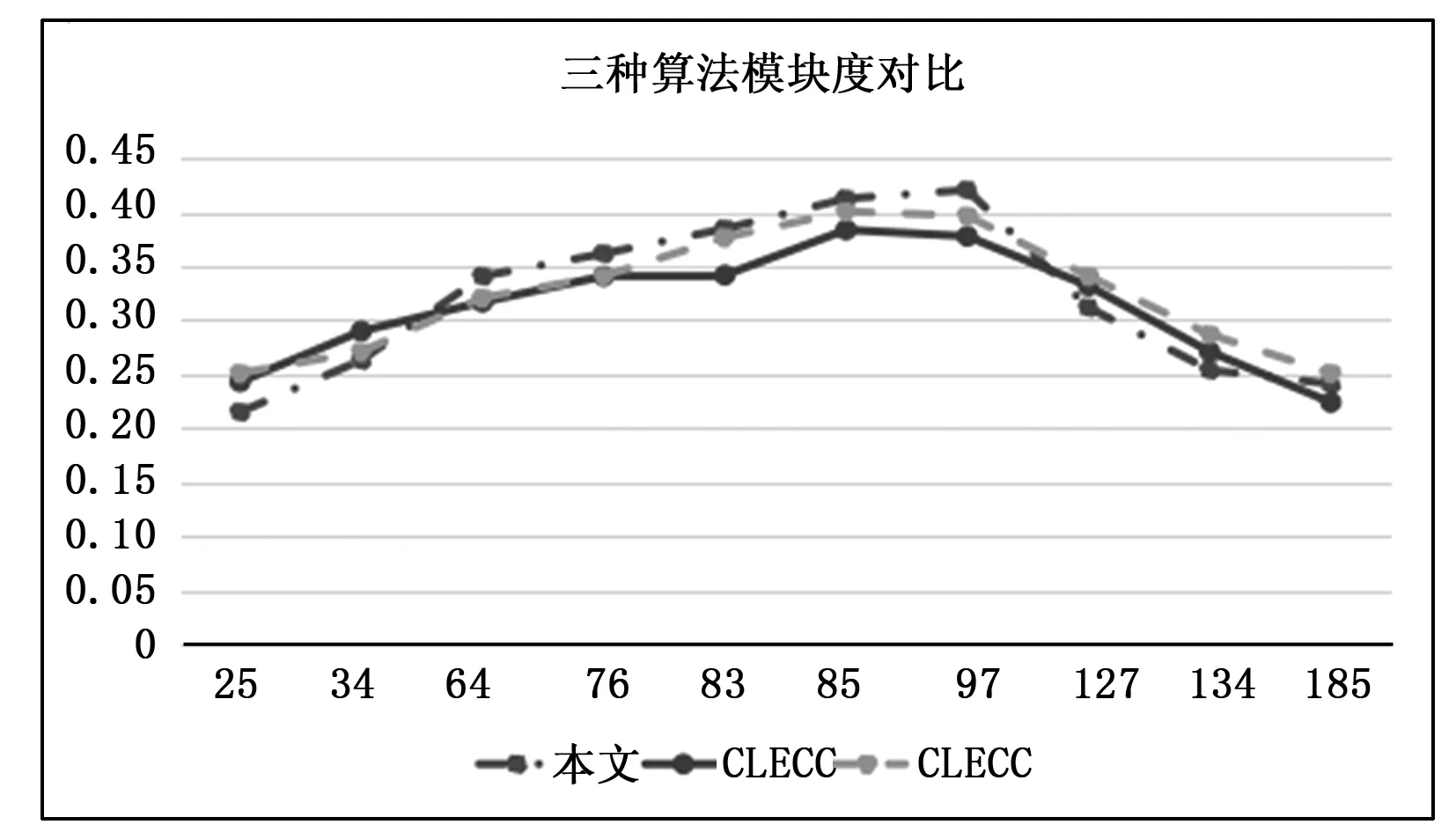
图9 IMDB网络模块度Q值对比

由图8和图9可以看出，不同算法在E-mail网络和IMDB网络上的模块度Q值不尽相同，本文算法相比CLECC算法和CLEDCC算法模块度更高，划分也更准确。

表1 三种算法运行时间比较(ms)

表1是本文算法和CLECC、CLEDCC三种算法对三个网络划分时间的对比，可以看出本文算法需要的运行时间更少，效率更高。

3 结论与展望

文中采用RA相似度和一种多层网络社团结构检测的模型，提出了一种基于层次覆盖的多层网络社团发现的新算法，并将算法在几个经典的多层网络进行了性能测试，均取得了不错的划分结果。实验的后一部分将本文算法与CLECC和CLEDCC两种算法作了比较，结果表明，不论在模块度值还是算法运行效率上都有所提高，避免了没有直接相连节点无法正确划分的情况，避免了对多层网络划分的局部性。