基于GLONASS的双基合成孔径雷达的预处理算法研究

，，，，

(湖北大学, 计算机与信息工程学院，武汉 430062)

0 引言

GLONASS-BSAR是一类被动式双基合成孔径雷达。该雷达系统的发射机为俄罗斯导航卫星GLONASS，而接收机可以搭载在卫星、飞机、汽车上或者直接部署在地面。

该雷达系统拥有安全性强，观察角度丰富，系统稳定性好，部署成本低等技术优势，已成为雷达业界的研究热点[1]。

双基合成孔径雷达的预处理是该系统能够工作的第一步，也是最重要的步骤。预处理的目的是为接收信号提供时间延迟、多普勒以及相位参考，从而将时钟滑移和振荡器漂移被从输出信号中消除，保持双基雷达发射机与接收机的信号相干性，实现信号同步。在信号同步研究方面，已有不少相关研究与成果，例如：文献[1-2]使用锁相环(PLL)来跟踪直达信号的多普勒和相位；文献[3-5]使用基于GPS的技术来实现双基合成孔径雷达的时间和相位同步；文献[6-7]研究了基于Envisat作为发射机和固定接收机的雷达系统架构的信号同步问题。然而，以上方法均不适用于具以导航卫星作为发射机的双基合成孔径雷达。第一个原因是其信号结构比上述提到的合成孔径雷达信号结构复杂，并且携带了导航电文，该信息的存在严重影响了信号的相干性；第二个原因则是GLONASS-BSAR雷达系统接收功率远小于上述提到的专用成像雷达接收信号的功率，导致接收信号信噪比极低，信号处理复杂度大大增加，因此，传统的预处理方法不再适用。

本文提出了一种用于GLONASS-BSAR系统的预处理算法，该算法直接对GLONASS卫星发射的P码进行跟踪处理，并从中提取同步参数。本文第1节将对GLONASS信号结构进行介绍。第2节详细描述预处理算法。第3节给出实测数据预处理结果。第4节分析该算法的复杂度。

1 GLONASS信号模型

GLONASS接收信号中包括三个要素，它们分别是：导航电文、伪随机测距码以及载波。其信号结构可以表示为：

(1)

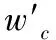
相对于C/A码，由于P码的带宽较宽，较利于成像。因此在本文中，拟直接对P码进行处理以获取其信号参数。

2 预处理算法

GLONASS-BSAR雷达系统装载了两副接收通道。第一副通道为直达波通道，该通道使用全向天线直接接收来自GLONASS卫星发射的信号。另一副通道为雷达波通道，该通道采用高增益定向天线获取成像区域的反射信号。两副通道使用相同的时钟以及本地振荡器，因此在时钟滑动以及本地振荡器漂移等诸多方面是相同的。由于在信噪比方面，直达波通道接收信号高于雷达波接收信号，因此使用直达波信号进行该雷达系统的预处理，提取接收机与发射机之间的时间偏移、频率偏移、相位偏移，导航电文等信息，实现该系统的同步。通过直达波接收信号获取的上述信息，作为输入引入雷达波通道接收信号，能够消除其各项误差，实现雷达波信号的同步。同步处理后的雷达波信号用于观察区域的成像处理。由于本文重点讨论预处理算法，因此雷达波信号的接收方法以及后续的成像算法不在本文的讨论范围，其相关内容不再赘述。

预处理包括坐标处理，直达波信号参数估计以及产生参考信号，其信号处理流程图如图1所示。

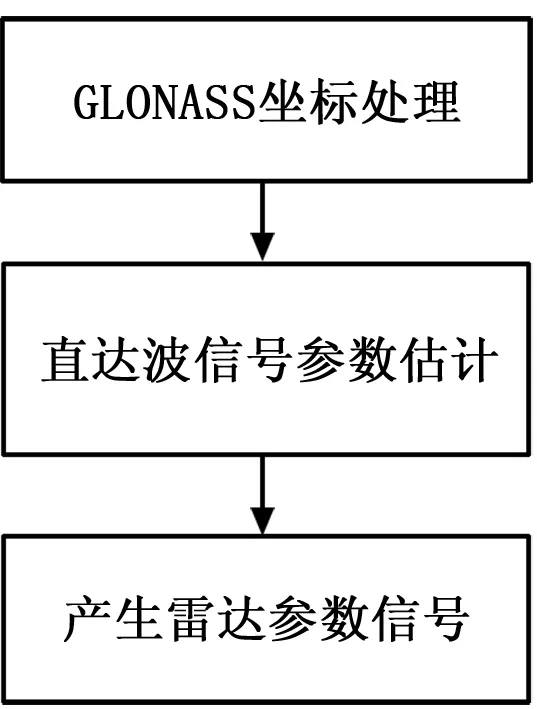
图1 GLONASS-BSAR预处理信号流程图

2.1 坐标处理

坐标处理用于快速估计直达波接收信号的时间误差、频率误差以及相位误差的理论值。坐标处理的第一步是对卫星轨道进行建模，提取实时坐标，并转化为在直角坐标系中的表示。本文将GLONASS的TLE参数作为SGP4/SDP4标准轨道模型的输入，提取时间间隔为1 s的以大地坐标系(LLA)为参考的实时卫星坐标信息。接着将该坐标变换为以地心地固直角坐标系(ECEF)为参考的表示，依据公式如下：

x=(N+h)cosφcosλ

(2)

y=(N+h)cosφsinλ

(3)

z=[N(1-e2)+h]sinφ

(4)

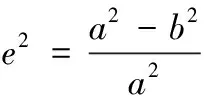
(5)

(6)

其中:x、y、z分别为ECEF中的坐标，φ、λ、h为LLA中的纬度、经度和高度，e为椭球偏心率，a、b分别为基准椭球体的长半径与短半径；N是圆曲率半径。

由于GLONASS的发射信号长度为1 ms，因此，需要将上述获取的卫星坐标采样频率提高至1 000 Hz。本文拟采用拉格朗日插值的方法将原始的以1 s为采样间隔的数据转换成以1 ms为采样间隔的数据，插值因子为1 000。使用公式如下：

(7)

其中:(xi，yi)为原始的卫星坐标，x为插入点的时间，Ln(x)为该时刻对应的坐标。

接着，估计出直达波接收信号的理论实时多普勒历史，推导公式如下：

(8)

(9)

(10)

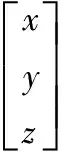
2.2 直达波信号参数估计

GLONASS-BSAR系统的直达波接收信号可以表示为：

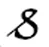
j×c[t-τ(t)]dC[t-τ(t)]e[-j(2πfd(t)t+φ(t) )]

(13)

式中，τ是瞬时信号传播延迟，fd是由GLONASS卫星与雷达接收机相对运动产生的多普勒频率，φ是信号相位信息。将式(13)整理成二维矩阵形式，矩阵有n排，每排的信号长度为1 ms，表示为：

s(tn,u)=p[tn-τ(u)]dP[tn-τ(u)]e[j(2πfd(u)tn+φ(u))]+

jc[tn-τ(u)]dC[tn-τ(u)]e[-j(2πfd(u)tn+φ(u))]

(14)

其中:tn从0到1 ms，u从-T/ 2到T/ 2;T是该雷达系统的观测时间。

接下来拟采用匹配滤波方法对P码的时间误差、频率误差以及相位误差进行估计。本地匹配滤波器构造表达式为：

(15)

匹配滤波的结果可以表示为：

MF(tn,u)=s(tn,u)○*sref(tn,u)=

cfP[tn-τ(u)]dP[tn-τ(u)]e[j(2πfe (u) tn+φ(u) )]+j×

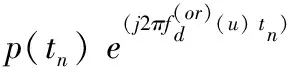
dC[tn-τ(u)]e[-j(2πfe (u) tn+φ(u) ) ]

(16)

其中:○*是相关运算，cfP[tn-τ(u)]是GLONASS-BSAR雷达系统接收的直达波与本地匹配信号匹配后产生的包络。

在式(16)中的第二项，由于P码和C/A码的相关性较弱，因此该项近似为零。因此式(16)可以化简为:

MF(tn,u)=s(tn,u)○*sref(tn,u)=

cfP[tn-τ(u)]dP[tn-τ(u)]e[j(2πfe(u)tn+φ(u))]=

cfP[tn-τ(u)]e[j(2πfe(u)tn+φP(u)+φe(u)+φn(u))]

(17)

式(17)可以看出，匹配滤波后的信号包含四个单独的相位项，其中φP(u)是由信号传播引入的相位历史，该信息用于后续的雷达二维成像。φe(u)包含所有类型的相位误差，例如振荡器漂移，大气误差等，该项属于本雷达系统参数，两接收通道均表现出相同的特性。φn(u)为导航电文引入的相位。

将相邻采样点出的相位依次求差值，可以得到：

Δφ(u)=φ(u+PRI)-φ(u)=

ΔφP(u)+Δφe(u)+Δφn(u)

(20)

在式(20)中，第一项ΔφP(u)和第二项Δφe(u)近似为零，其相位的翻转主要来自于导航电文的相位差。因此，可以根据式(20)中曲线的变换来获取导航电文信息φn(u)。

由于φP(u)能够通过接收机与发射机的坐标进行计算，因此，可以获得系统相位误差φe(u)。

2.3 本地同步信号的产生。

根据预处理获得的各项时间、频率、相位分量以及导航电文，本地同步信号可以表示为：

(22)

3 实测数据结果与性能分析

3.1 实测数据结果

本节使用实验数据对上述提出的GLONASS-BSAR系统的预处理算法进行了验证。实验数据来源于伯明翰大学微波雷达系统实验室，其相关实验参数如表1所示。

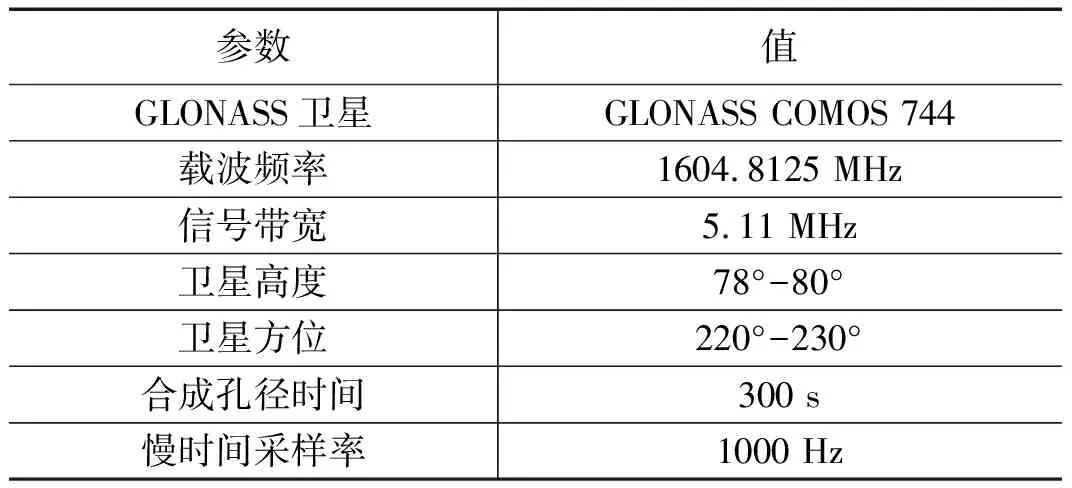
表1 实验参数

采用本文提出的预处理算法得出的同步结果如图2至5。图2为P码的时间延时，图3为P码的多普勒，图4为解码后获取的P码携带的导航电文，图5为去除导航电文后P码在慢时间方向上的频谱。从图5可以看出，去除导航电文后，P码在慢时间方向上的频谱是一个较为理想的窗函数，和时域的Sinc信号互为变换。

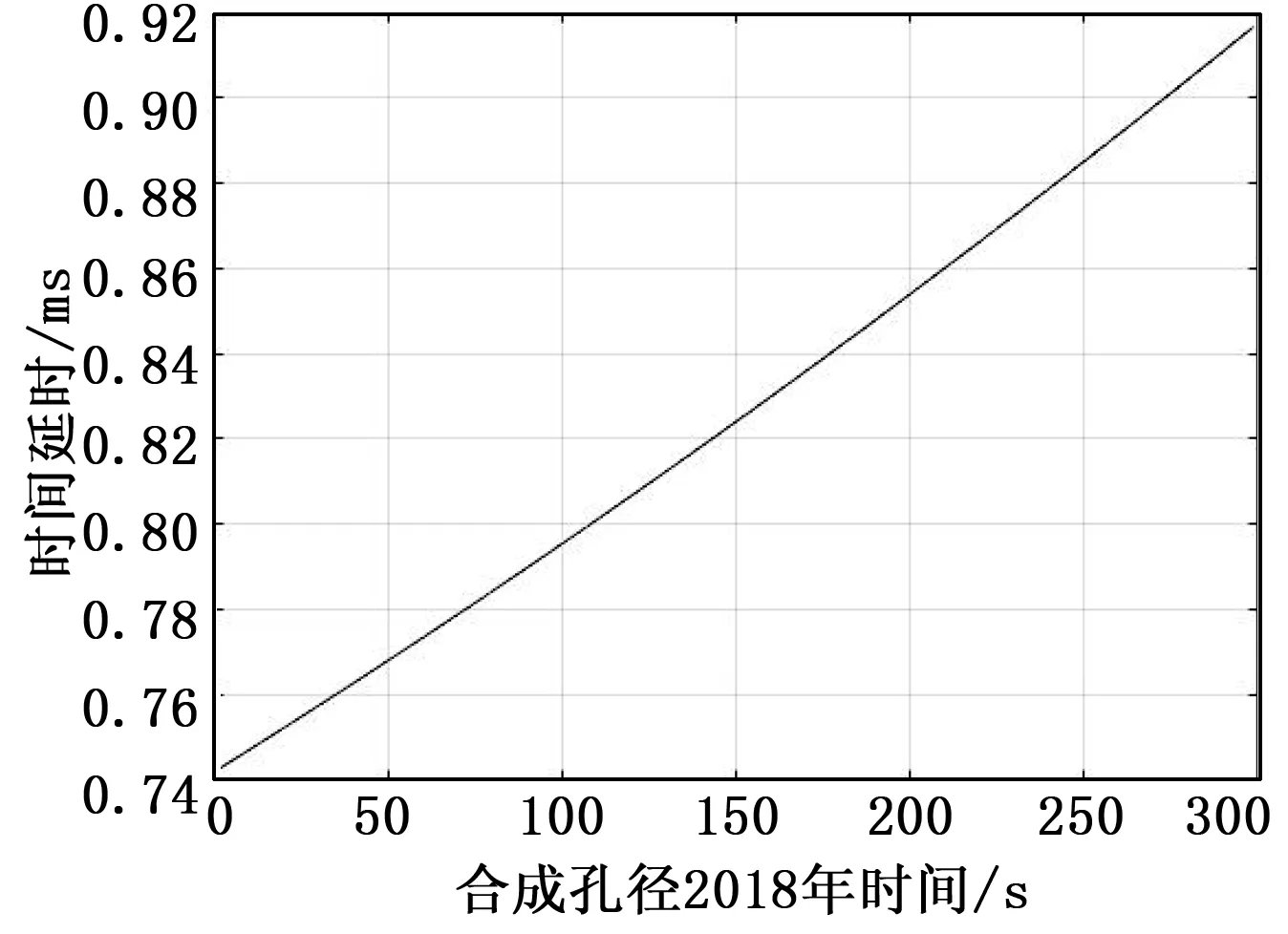
图2 跟踪的P代码延迟

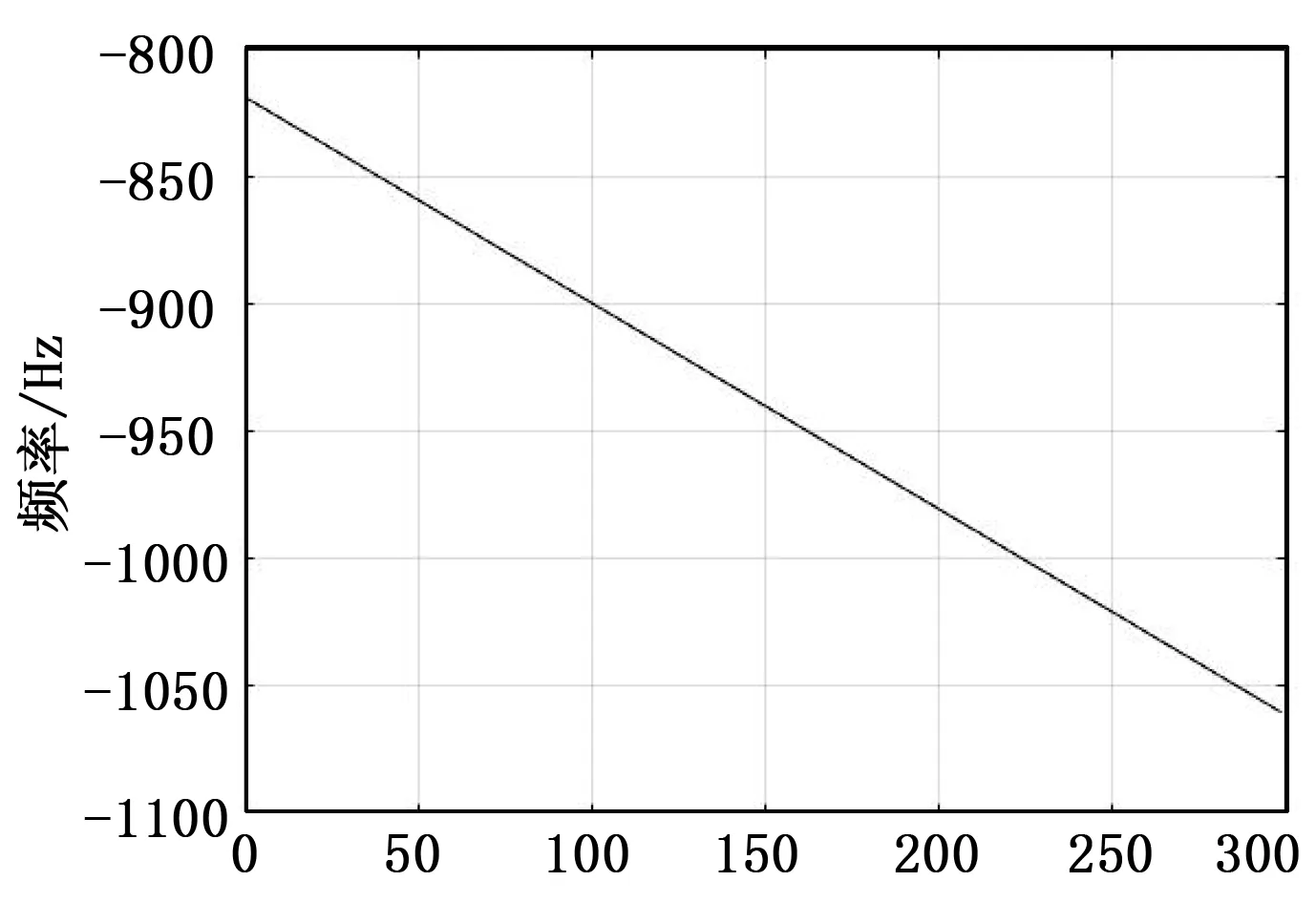
图3 跟踪的P码多普勒

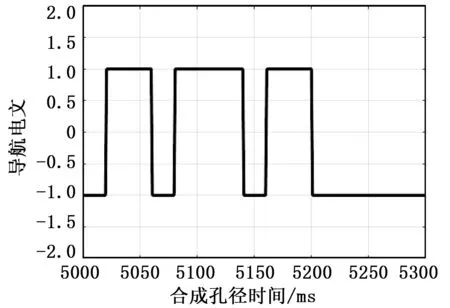
图4 导航信息图

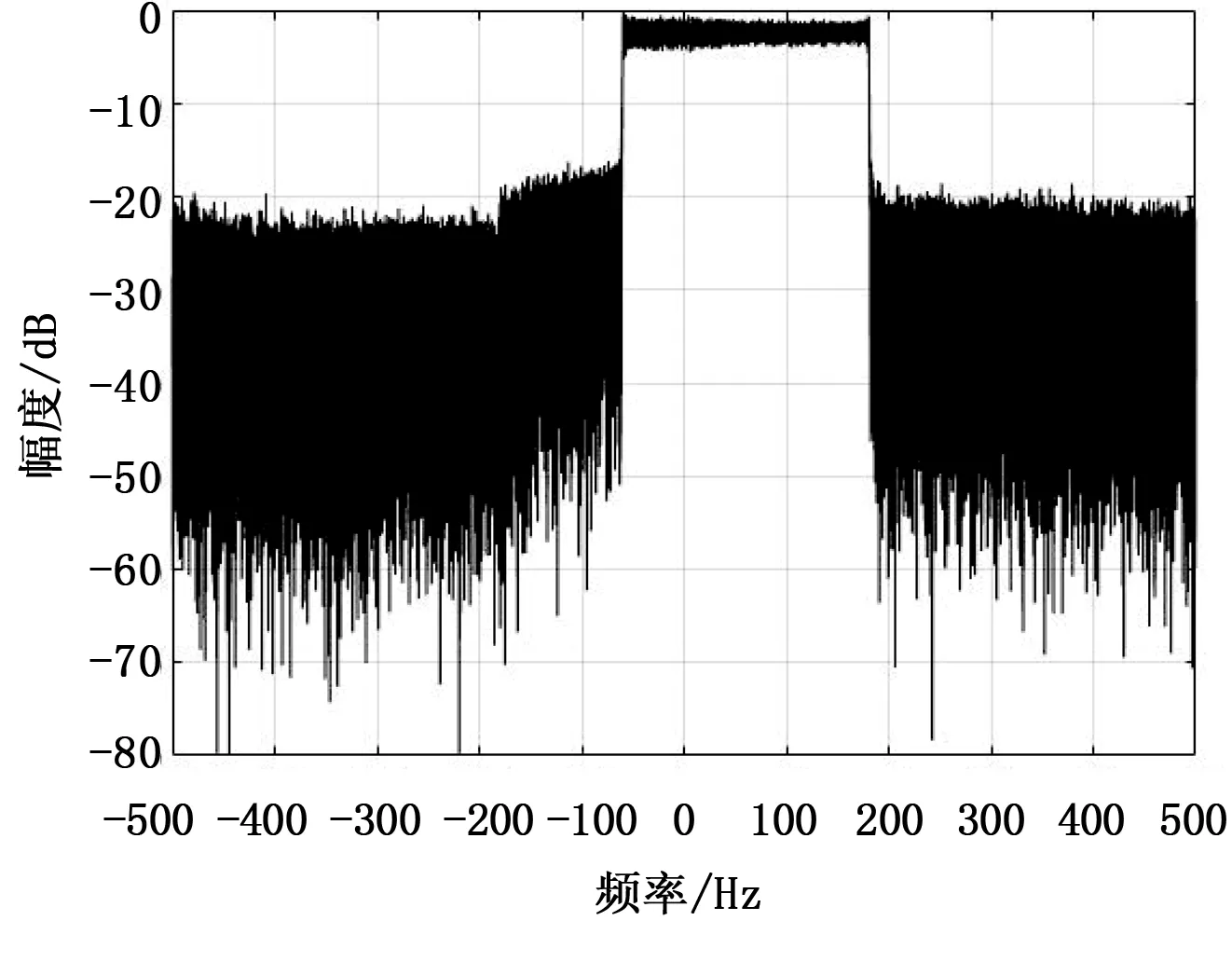
图5 去除导航消息后的P码慢时间信号频谱

将预处理获取的时间延时，多普勒频率，导航信息，相位信息，代入GLONASS-BSAR直达波接收信号，通过Back-Projection 算法，获得二维图像如图6。

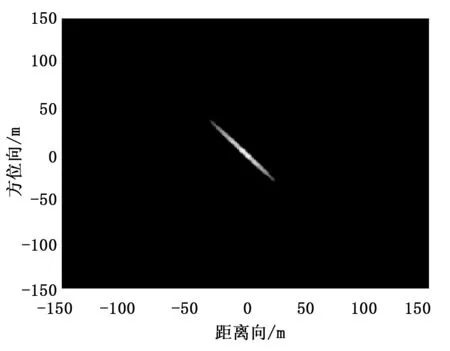
图6 采用直达波信号进行的成像结果

从图6可以看出，该图像是一个聚焦完好的点目标成像结果。因此可以认为，本文提出的预处理算法将直达波接收信号的时间延时，多普勒频率，导航信息以及相位信息精确的提取出来，证明的该算法的准确性和有效性。

3.2 算法复杂度分析

上述描述的预处理方法直接对P码进行跟踪。通过快速时间方向上的匹配滤波，从而获得每个PRI处的瞬时P码延迟；之后得到的信号又经历了相变检测器的处理，去除了导航消息并被解码。将跟踪的相位历史与理论预期的相位历史进行比较，获取了相位误差，最后通过相邻PRI之间的瞬时相位差找到P码多普勒。

该算法的复杂度分析如下：假设一个复数乘法和一个复数加法都占用一个操作数，则N阶(快速傅里叶变换)FFT和(快速傅里叶逆变换)IFFT需要Nlog2N个复数加法和0.5Nlog2N个复数乘法，其总和包括1.5Nlog2N个操作数。一个慢时间周期中数据使用处理算法需要的和/减以及FFT / IFFT的数量在下表中列出：

表2 算法复杂度

表中N是一个慢时间周期的采样点数，为50 000。对于5分钟数据，快速预处理算法需要的总运算数为：

运算总数=12 000×5×50 000+270 000×5×

50 000×log250 000=320 G

使用TI最先进的DSP C66x 处理器，对5分钟观测时间获取的数据进行预处理，只需要5分钟。

4 结束语

本文提出了一种采用GLONASS卫星作为发射机的外辐射源合成孔径雷达快速预处理算法。该算法直接对P码进行处理，能够高效、精确的获取P码的时间延时、频率偏移、相位偏移以及携带的导航电文。实测数据验证结果表明，该算法能够精确的估计GLONASS-BSAR雷达系统引入的时间延时、频率、相位以及导航信息，实现该雷达系统发射机与接收机的时间同步以及相位同步，为后续的成像处理提供技术可行性。此外，该算法具有一定的高效性，理论计算与实际测试均表明，对5分钟观测时间获得的直达波接收信号进行处理，该算法只需要5分钟。

后续的研究方向将主要聚焦在如何对该算法进行优化，获得更好的实时性。