直流配电系统潮流可行解与电压稳定性分析方法
张 聪, 彭 克, 徐丙垠, 陈 羽, 赵学深, 赵曰浩
(山东理工大学电气与电子工程学院, 山东省淄博市 255000)
0 引言
石油、煤炭等传统能源的日渐枯竭及环境污染的日益加剧,使得开发利用新能源和可再生能源成为中国经济可持续发展的迫切需求。新能源发电接入电网可以有效减少传统火力发电的碳排放,但光伏发电、储能等直流型分布式电源及电动汽车等直流负荷的增加,给传统配电网带来了多方面的影响。目前国内配电网主要采用交流供电方式,需要经过多个电能变换环节才能满足直流源荷的接入需求,供配电的效率受到影响,同时导致运行控制复杂,系统的安全稳定问题越来越严重。
基于柔性直流技术的直流配电网具有提高供电容量、减小线路损耗、改善用户侧电能质量、隔离系统故障等一系列优点[1-3],同时,直流配电网也为直流分布式电源、电动汽车等的灵活接入提供了良好的条件。电力电子装置使得配电网的组网形态及控制方式更加灵活多样,直流系统通过DC/DC变换装置等可实现不同电压等级之间的互联,换流器灵活的控制方式可以实现交直流潮流的相互转供,有利于系统的可靠稳定运行。未来的智能配电网将会是一个交直流全面互联的复杂系统。
与直流输电系统不同,直流配电系统直接面向负荷供电,因此系统的电压稳定尤为重要[4],目前对其稳定性已有部分研究。例如:文献[5]针对多端柔性互联装置采用主从和下垂控制的情况,构建了交直流混联配电系统的戴维南等效电路,利用奈奎斯特稳定判据确定了负阻抗稳定边界;文献[6]研究了采用下垂控制的直流配电网小扰动稳定性,并讨论了换流器阀控时间和功率外环比例参数对系统小扰动稳定性的影响;文献[7]研究了交直流配电系统之间的交互影响特性,并提出了基于有源补偿的稳定控制策略;文献[8]对直流配电系统的稳定性判据进行了综述,并提出了基于无源理论的稳定性分析方法;文献[9]分析了多母线结构的中压配电系统的稳定性,并基于无源理论设计了前馈控制器以保证系统的稳定性。但上述研究大多从装置层次的稳定设计出发,而对全局系统级的稳定性研究较少。
系统潮流是分析全局电压稳定的一种有效方法,通过潮流可行解即可获知系统的运行状态。例如:文献[10]提出交直流完全解耦的潮流可行解获取方法,文献[11-12]提出计及换流站不同控制策略的交直流配电系统潮流计算方法,可以为系统运行方式调整提供准确的信息;文献[13]通过求解系统潮流与柔性装置进行协调实现直流配电系统的稳定运行。但上述研究主要侧重于潮流求解方法,潮流可行解的存在性与唯一性分析尚未涉及。近年来已有学者针对交流配电系统开展研究,证明了辐射状交流配电系统潮流可行解的唯一性[14],文献[15]在此基础上提出了三相配电系统潮流解析化求解方法,避免了非线性潮流方程的迭代求解,为系统运行方式调整提供了更为直接的理论基础,文献[16]研究了低压直流电网的潮流解问题,但未涉及采用下垂控制的多端互联直流配电系统及稳定性分析。
通过潮流解的存在性与唯一性,可更为直观地进行运行方式分析、电压稳定分析与评估等[17-18]。直流配电系统只存在有功潮流,与交流配电系统存在较大的差别,因而研究其潮流解的存在性与唯一性,可以为其电压稳定分析提供更为直接的理论与方法。本文通过巴拿赫不动点定理证明了直流配电系统不同控制方式下潮流解的存在性与唯一性,并基于潮流可行解提出了电压稳定的分析方法,可快速评估直流配电系统接入负荷后的稳定性,避免了复杂的连续潮流计算。
1 直流配电系统拓扑与控制策略
柔性直流配电系统的基本拓扑结构可分为两端供电方式和多端供电方式两种,图1给出一个基于全控型双向换流器的多端柔性直流配电系统示例。
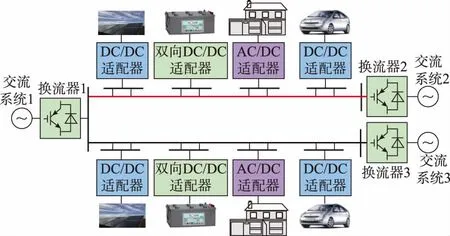
图1 多端柔性直流配电系统拓扑Fig.1 Topology of a DC distribution system based on multi-terminal voltage source converters
多端柔性直流配电系统相对交流系统网络结构更为灵活多样,交流侧通过换流器与直流配电系统互联,系统潮流具有多向流动性,换流器灵活的控制方式可以实现交直流潮流的相互转供,有利于系统的可靠稳定运行。多端柔性直流配电系统运行上的灵活性也为控制系统带来了新的挑战,需要更为可靠稳定的控制策略对换流器进行协调控制。其控制策略一般采用主从控制或者对等控制:主从控制由一个换流器对电压进行控制,其余换流器采用恒功率控制策略,具有较好的运行稳定性;对等控制则通过各换流器的下垂系数协调功率输出,可以实现各换流器功率的均衡分配。因此,本文主要针对采用这两种控制策略的直流配电系统进行分析。
2 潮流解与电压稳定的关系
传统交流输电系统的潮流方程是一组非线性代数方程,通常会存在多个解[19]。图2所示为典型的PV曲线,图中P0为潮流初始解。潮流的多解性意味着节点具有多条PV曲线,随着负荷水平的增加,其两组电压解A与B越来越接近,直到负荷达到最大值Pmax时A与B重合,即在该点发生鞍结分岔,而当系统负荷继续增加时,潮流方程将会无解,在该点发生鞍结分岔,也即系统的静态电压稳定极限点[20]。因此,利用系统潮流方程的可解性,即可判断系统的电压稳定性,但通常需采用连续潮流进行计算求解,而且很难求出潮流的所有解。
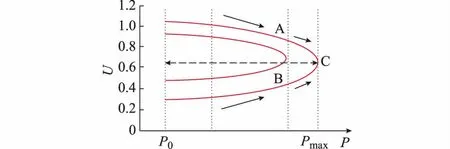
图2 典型PV曲线Fig.2 Typical PV curves
从小扰动稳定角度考虑,采用解A对微分方程线性化后,其特征根均在左半平面,采用解B对微分方程线性化后,存在右半平面的特征根,即系统不稳定,点C即为系统的临界稳定点。
直流配电系统因没有无功功率传输,导纳矩阵与电压电流相量等均为实数矩阵,虽其潮流方程也是一组非线性代数方程,但其潮流解具有新特征。
3 直流配电系统潮流可行解的唯一性
直流配电系统的潮流方程可以采用功率方程或电流方程描述,两者在本质上并无不同,下面以电流方程为例进行介绍。以节点注入电流描述的方程可写成如下形式:
(1)
式中:I1和U1分别为平衡节点的电流和电压;I2和U2分别为其他节点的电流和电压;Y11为平衡节点的自导纳矩阵,Y12为平衡节点与非平衡节点的互导纳矩阵,Y21为非平衡节点与平衡节点的互导纳矩阵,Y22为非平衡节点的自导纳矩阵。
下面针对主从控制及下垂控制两种策略分别对其潮流进行分析。
1)主从控制
采用主从控制的直流配电系统中,平衡节点电压是给定的,除平衡节点外其他节点的电压为:
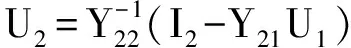
(2)
考虑系统中存在恒功率负荷或电源、恒阻抗负荷与恒电流负荷,统一以注入电流形式表达,即
(3)
2)下垂控制
当采用下垂控制时,换流器输出功率可表示为:
P1=Pref-K(Udcref-Udc)
(4)
式中:P1为换流器输出有功功率;Pref为换流器有功功率参考值;K为下垂系数;Udcref为换流器直流电压参考值;Udc为换流器直流电压。
换流器有功功率参考值、直流电压参考值及下垂系数固定的情况下,将式(4)进一步整理可得:
P1=(Pref-KUdcref)+KUdc=Pconst+KUdc
(5)
可以看出,下垂控制的输出特性可以等效为恒功率与恒电流的线性组合,此时U1为未知量需要进行求解,可与U2采用交替迭代的方法进行求解,求解U1时U2作为已知量,求解U2时U1作为已知量,具体如式(6)所示:
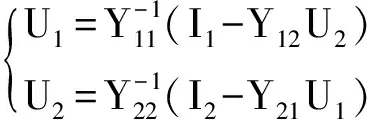
(6)
3.1 巴拿赫不动点定理与相关推论
巴拿赫不动点定理又称为压缩映射定理,是关于代数方程或者微分方程解的存在性和唯一性问题的一个重要定理,具体如下所述。
定理:若X为非空的完备度量空间。设F:X→X为X上的一个压缩映射,则存在唯一x0∈X使得F(x0)=x0。
下面对相关定义和推论进行介绍。
定义1:压缩映射
设X是度量空间,定义映射F:X→X,如果存在L∈[0,1),使得任意的x,y∈X,满足‖F(x)-F(y)‖≤L‖x-y‖,则称F为压缩映射,其中L为压缩因子。
定义2:极大范数
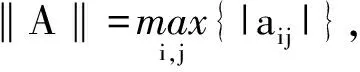
定义3:对角占优矩阵
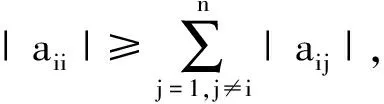
推论1:矩阵A为n×n阶矩阵,矩阵B为对角矩阵,则矩阵A与B的极大范数满足相容性,即
‖AB‖≤‖A‖‖B‖
(7)
常规矩阵的极大范数不满足相容性,但若相乘的右矩阵为对角矩阵,则满足相容性。
证明:定义矩阵C=AB,其中
则有cij=aijbjj,可见矩阵C中各元素均为矩阵A与矩阵B的元素乘积,满足
|cij|max≤|aij|max|bjj|max
(8)
推论2:若矩阵A为行对角占优矩阵,则其逆矩阵模值最大元素出现在对角元素中[21]。
3.2 潮流可行解唯一性证明
考虑到实际的电力系统运行中都有:
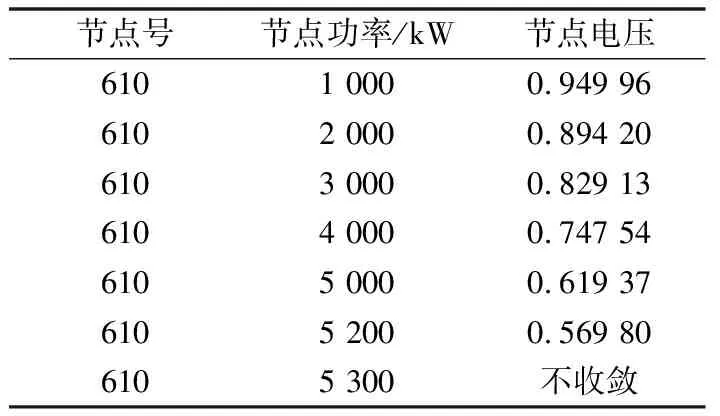
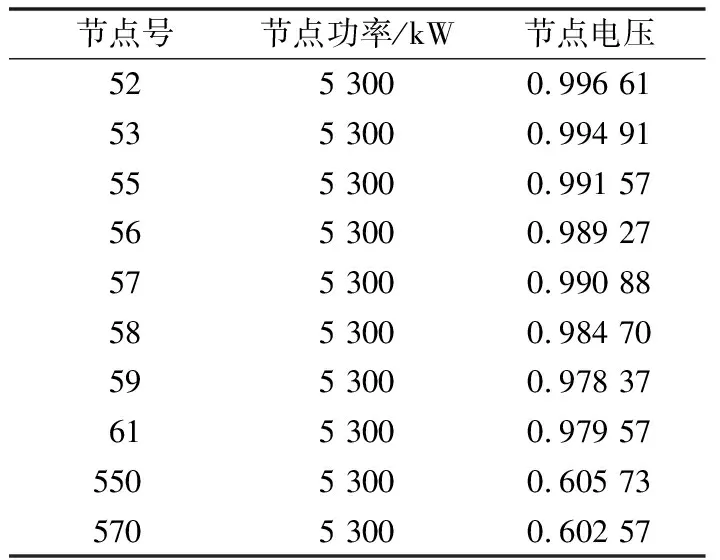
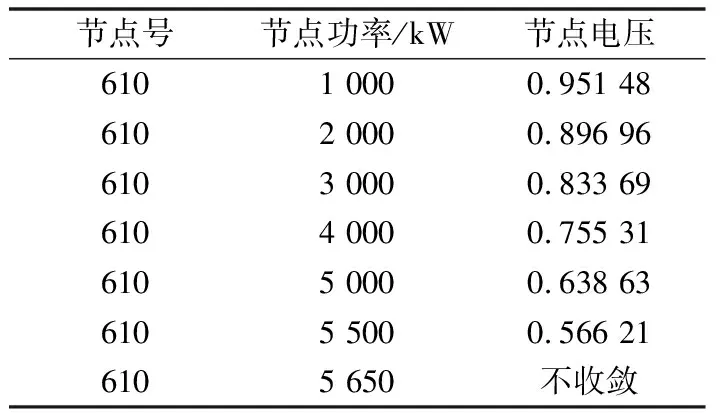
0 (9) 因此U∈[Umin,Umax]为完备度量空间,根据式(3)定义映射: (10) 下面将证明映射F为压缩映射。 1)主从控制 取Ua,Ub∈U2,D1=diag(P2),D2=diag(1/Ua-1/Ub),则有 (11) 记 (12) (13) 式中:Rmax为阻抗矩阵对角元素的最大值,即节点的戴维南等效电阻;Pmax为该节点对应的注入功率。 由戴维南等效电阻的定义可知,式(13)的分母为短路电流,分子为系统正常运行时的电流,通常正常运行电流要远小于短路电流,因此有L2<1,满足巴拿赫不动点定理。 此外,由于分布式电源接入后具有抬升电压的作用,其接入点电压有U>Umin,必然满足上述不等式,因此分布式电源接入与负荷不同,不存在传统意义上的失稳,但会造成电压越限。 2)下垂控制 取Ua,Ub∈U1,D3=diag(Pconst),则有 (14) 同理有 (15) 满足巴拿赫不动点定理,而且可以看出,影响下垂控制稳定性的主要是其恒功率输出部分。与主从控制类似,分布式电源接入后不存在传统意义上的失稳,但会造成电压越限。 为了更为直观地理解上述结论,下文以附录A图A1所示的两节点简单系统为例,进行简要的分析说明。 假设U1固定,由式(3)可得: (16) 整理得到U2的解为: (17) 根据式(12)可得: (18) 通过以上分析可以看出,若戴维南等效电阻最大的节点其注入功率满足: (19) 则该系统存在唯一可行的潮流解,即系统稳定。因此,通过式(19)可直观进行系统稳定性的判别,通过求解式(1)中导纳矩阵Y22的逆矩阵获取阻抗矩阵,取其对角元素的最大值Rmax,根据允许运行的最小电压可快速评估负荷功率接入极限,也即系统的静态电压稳定极限,避免了大规模的非线性连续潮流求解问题。 为验证本文理论分析的正确性,采用文献[21]中的直流配电系统算例进行测试。将交流系统等效后,通过三个换流器VSC1,VSC2,VSC3组成三端供电的直流配电网,如附录A图A2所示,具体算例参数可参见文献[11]。 1)情景1:主从控制。在直流配电网中,VSC1采用定电压控制,VSC2与VSC3采用定功率控制。通过形成直流配电网的导纳与阻抗矩阵,可得其节点610的戴维南等效电阻最大,有Rmax=0.470 9(标幺值)。通常情况下取电压范围为0.5 采用天津大学PFDG潮流计算软件进行校验,节点610接入不同负荷功率时的电压值如表1所示。可见,当节点610接入负荷功率5 300 kW时,潮流计算不收敛,系统失去稳定性。其他节点依次接入5 300 kW负荷时,各节点功率如表2所示。 表1 主从控制下节点610接入不同负荷时的电压Table 1 Voltage of node 610 with different load power under master-slave control mode 表2 其他节点接入5 300 kW负荷时的电压Table 2 Voltage of other nodes with load power of 5 300 kW 节点610接入不同分布式电源功率和其他节点分别接入5 300 kW分布式电源功率时的电压结果分别如附录B表B1和表B2所示。 通过计算结果可以看出,节点610为受负荷功率影响最为严重的节点,其他节点接入5 300 kW负荷时潮流计算均可计算收敛,也即系统稳定;接入分布式电源时,随着功率增加,潮流解始终存在,不会存在传统意义上的失稳,但会造成电压越限,同样,节点610为越限最为严重的节点。 2)情景2:下垂控制。VSC1,VSC2,VSC3采用下垂控制时,节点54,60,152均作为平衡节点处理,重新形成直流配电网的导纳与阻抗矩阵,可得其节点610的戴维南等效阻抗最大,有Rmax=0.442 7(标幺值)。通常情况下取电压范围为0.5 表3 下垂控制下节点610接入不同负荷时的电压Table 3 Voltage of node 610 with different load power under droop control mode 通过计算结果可以看出,节点610为受负荷功率影响最为严重的节点,接入5 650 kW负荷时,潮流计算不收敛,即系统失去稳定性,而其他节点分别接入5 650 kW负荷时潮流均能收敛,接入分布式电源的情况与主从控制类似,具体数据不再列出,同样不存在传统意义上的失稳,但会造成电压越限,节点610受影响最为严重。 基于柔性直流技术的直流配电网是未来智能电网的发展趋势。本文通过巴拿赫不动点定理证明了直流配电系统潮流解的存在性与唯一性,并基于潮流可行解提出了电压稳定的分析方法,通过算例测试验证了本文方法的有效性和正确性,结论如下。 1)直流配电系统由于只传输有功功率,除平衡节点外不存在电压可调节的节点,因此在平衡节点电压固定的情况下,其潮流可行解具有唯一性。 2)随着直流负荷的增加,直流配电系统会出现类似交流系统的鞍结分岔,导致系统不稳定,分布式电源的接入不会导致传统意义上的系统失稳,但会造成电压越限。 3)戴维南等效电阻最大的节点,即为系统的薄弱点,接入负荷或分布式电源后受影响最大,根据压缩映射定理压缩因子需满足的条件,可获取系统的静态电压稳定极限。 可以看出,直流配电系统的最优潮流也与传统意义上的最优潮流有所区别,必须对平衡节点进行调节才能实现最优目标。后续将进一步针对直流配电系统的最优潮流开展研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。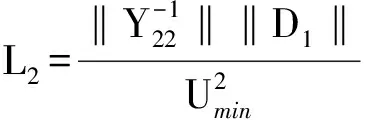
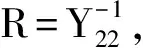
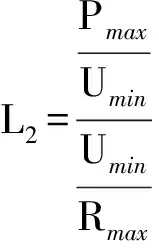
3.3 两节点系统分析
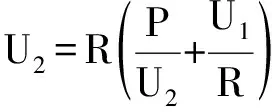
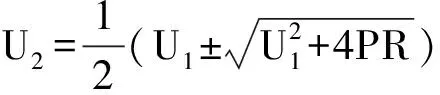
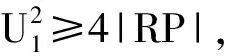
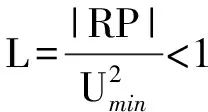
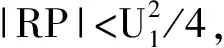
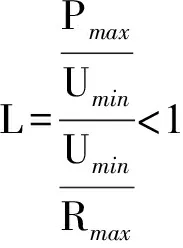
4 算例测试
5 结论

