基于生物质热电混合供能的城镇综合能源双层优化
许 健, 施锦月, 张建华, 郝 然, 陈奇芳
(1. 国网河北省电力有限公司检修分公司, 河北省石家庄市 050000; 2. 国网河北省电力有限公司石家庄供电分公司, 河北省石家庄市 050000; 3. 华北电力大学电气与电子工程学院, 北京市 100000; 4. 上海交通大学电子信息与电气工程学院, 上海市 200240; 5. 北京交通大学电气工程学院, 北京市 100044)
0 引言
由于传统发展方式粗放、能源结构和产业结构不尽合理,中国雾霾污染问题已影响到了社会生产、人民生活等各个领域。从大气污染物的结构来看,雾霾污染最主要的原因是煤炭粉尘[1-2]。目前,中国北方地区燃煤供暖面积超过了1010m2,燃煤供暖占90%以上。为加快提高清洁能源供暖比重,“煤改气”和“煤改电”等政策陆续颁布,但随着各地对“煤改”政策陆续进行落实和实施,效果并不明显[3-4]。因此如何改善供暖替代能源的经济性、提高供暖替代能源的能源利用效率成为推动“煤改”政策的关键问题[5]。
能量枢纽(energy hub,EH)作为多种能源和负荷需求的能源转换单元[6],是电热供能系统连接、转换以及运行控制的重要途径。通过能量枢纽对热电气系统进行运行与协同调度的问题,已有了大量的研究[7-13]。针对生物质、太阳能等可再生能源充分的城镇地区,使用能量枢纽将可再生能源转换为热能进行供暖[14],既可改善燃煤带来的环境污染问题,又可以弥补电代煤供暖面临的电费高的问题。
目前,对于生物质热电联供的研究,国内外学者已对该主题进行了相关探讨,并获得一些初步成果[15-20]。文献[15]为反映生物质混煤系统综合性能,基于能值理论,提出了4个评价指标,对生物质能掺烧于不同容量、不同燃煤发电/热电联产(combined heat and power,CHP)系统进行了可持续性分析评价;文献[16-17]对不同生物质燃料进行CHP的工程规划与建设思路进行介绍,并对其节能经济性能进行了详细分析;文献[18]从能耗和温室气体排放角度,对生物质作为燃料参与CHP进行比较分析;文献[19-20]提出并介绍了基于不同能源构成的生物质CHP实现技术和运行模型。
上述研究成果为后续工作奠定了基础,但仍普遍存在以下两个重要问题,亟待进一步研究解决:①多数研究着重于对生物质CHP的效益和能效等方面进行分析评价,而对生物质CHP在能源系统中具体运行模型与运行方式的研究不够充分;②多数生物质CHP研究着重于在生物质发电的基础上直接加入余热回收装置,能源利用效率的提高效果不够显著,与其他新能源相比,生物质热电联供的市场竞争力不足。
针对上述问题,本文提出一种适用于城镇地区多种新能源高效消纳的综合能源运行双层优化方法。在生物质CHP的基础上加入补燃机制,建立多个不同输入能源的可补燃CHP机组的联合运行优化模型。该模型详细计及了配电网、天然气、光伏和生物质等多种能源的协同运行,并将电热供能系统作为整体对其经济性和能效进行统筹调度,同时设计了差分帝国竞争算法进行求解验证。与文献中的生物质CHP方法相比,本文方法进一步提高了生物质CHP供能的经济性和能源利用效率,提高了生物质供能的市场竞争力。
1 城镇综合能源供给系统
1.1 生物质供能模型
生物质供能主要利用农业和林业生产中产生的有机废弃物作为燃料,一般通过粉碎或颗粒化的处理后直接燃烧发电,甚至一些经过分类处理的城市垃圾也可回收利用,通常采取直接燃烧或气化等方式进行发电。城镇地区作为农作物集散地,生物质资源丰富,通过直接燃烧的发电技术产生绿色电力,不仅可增加清洁能源比重,还可以增加农民收入,缩小城乡差距。
生物质燃料经气化处理后可直接燃烧发电,依据发电容量不同一般有3种方式[1],如图1所示。图中:δ1至δ5为转化效率。依据文献[19,21],本文选取的研究对象为园区级用户,根据负荷水平选择微型燃气轮机发电的方法。一般由微型燃气轮机直接发电的转化效率在20%左右,用能效率低。本文在微型燃气轮机发电的基础上,配置带补燃装置的余热锅炉,改变CHP机组供热效率,从而提高整体能源利用率ηE。

图1 生物质气化供能原理Fig.1 Principle of biomass energy supply through gasification technology
CHP补燃装置的工作原理为:补燃燃料直接喷入废气回收的烟道中与废气混合燃烧,利用燃机排烟中的过余氧气作为燃料的氧化剂,利用锅炉入口烟道的内部空间作为补燃燃室,燃机排气余热和补燃带入锅炉的热量共同与炉水换热后产生蒸汽或热水,提高了CHP机组产热效率。
生物质和天然气作为发电燃料,经过微型燃气轮机后产生废气,二者产生的废气皆经上述过程进行补燃供能,其机组的补燃效率参数相同。根据文献[22]提供的补燃机组实验数据,用线性模型对CHP补燃率A(t)、热电比VC(t)、响应油耗量PO(t)进行拟合得到:
(1)
式中:Ka1,Ka2,Kp1,Kp2为拟合系数。
1.2 光伏发电模型
采用光伏电池单二极管的等效物理模型,模型建立后基本可以将光伏电池等效为电流源。输出电流I可以表示为[23]:
(2)
式中:n为二极管特性因子;k为波尔兹曼常数;T光伏电池绝对温度;Rs为串联电阻;Rh为并联电阻;Ip为光生电流;V为输出电压;I0为反向饱和电流;q为电子电量。
光伏电池的输出电流不仅与温度和光照强度有关,也与内部等效电路的几种电阻参数有关。在此模型的基础上,通过日前温度和光照强度的预测值得到对第2日光伏发电最大功率的预测值。
1.3 综合能源系统运行框架
选取城镇中建设运行成本较低、应用广泛的生物质、光伏、天然气和电网为能量输入,通过补燃设备优化生物质和天然气CHP机组热电运行状态,设计城镇综合能源系统典型运行框架如图2所示。

[LeLh]T=
[PRPPPBPGPO]T
(3)
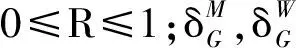
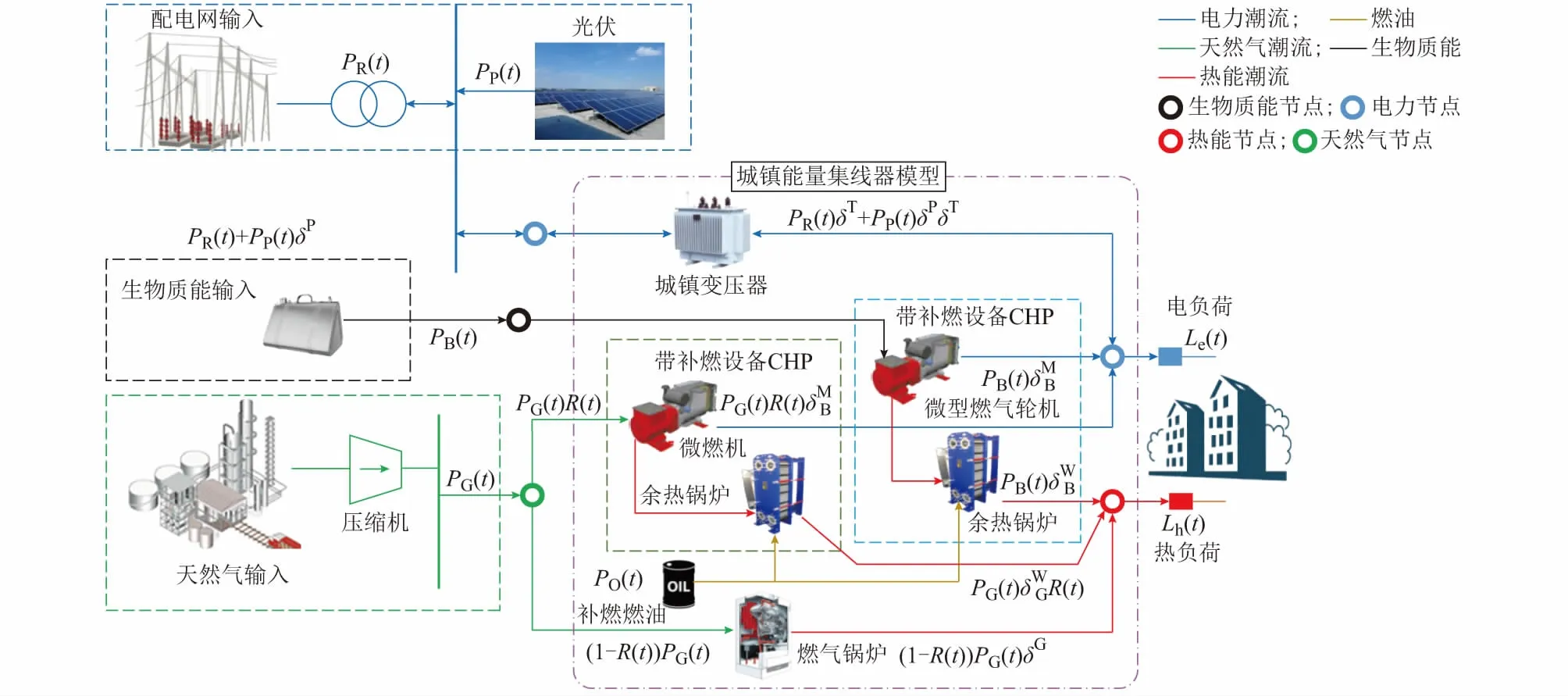
图2 城镇综合能源系统Fig.2 Rural integrated energy system
热电比VC为CHP输出热功率与电功率的比值,以天然气和生物质为燃料的CHP机组,其热电比可分别表示为:
(4)

结合式(1),补燃燃油PO(t)与δW的关系为:
δW=δMVC=δMKa1(Kp1PO(t)+Kp2)+Ka2
(5)
式中:δW和δM分别为天然气CHP机组或生物质CHP机组转化为电和转化为热的功率。
本文中认为天然气供能的CHP机组与生物质供能的CHP补燃装置具有相同的机组特性。由于补燃燃料仅起调节作用,不直接作为能源输入,为降低成本,本文涉及的天然气和生物质补燃装置皆采用工业废油。
2 城镇综合能源双层优化调度策略
双层优化模型是具有双层递阶结构的系统优化模型,下层优化问题基于上层决策给定的方案,将下层决策的最优值反馈到上层,上层再根据下层的最优值反应做出符合全局最优效益的决策[24]。本文以城镇地区热电混合供能系统为研究对象,将REH的用能成本优化问题和REH的用能效率提高问题考虑为双层优化模型,如附录A图A1所示。上层模型描述了REH的能源分配策略,以热电负荷和光伏预测数据以及下层上传的两个CHP热电比为基础,通过全局优化算法求解出能源在电网、天然气供能和生物质供能中的全局优化调度策略,实现对宏观能源的分配与控制;下层模型为机组的微观能效优化,依据当前能源与负荷的分配状态,对天然气供能和生物质供能的CHP机组的运行情况分别进行相应的调整,在上层能源分配的结果中实现下层用能效率优化。在此过程中,天然气和生物质接入的CHP机组最佳运行热电比发生改变,上层策略根据下层优化的结果重新优化,循环往复,直至最优。
2.1 上层能源分配优化模型
1)目标函数
上层优化以综合用能成本最小为目标,以天然气分配系数R(t)和生物质输入功率PB(t)为决策变量。用能成本的目标包括综合运行成本C(t)和污染物排放成本G(t)。
(6)

(7)
式(7)中:等号右侧4项分别为购气成本、电价成本、补燃燃油成本和生物质成本;λG(t),λR(t),λO,λB分别为天然气、电能、补燃燃油和生物质的能源价格;QB为生物质的低热值;QG为天然气的低热值,取9.97 (kW·h)/m3;QO为燃油低热值,取11.917 (kW·h)/kg。本文所涉及的物理量皆为功率,通过公式3.6×106J=1 kW·h将单位统一为kW·h。
污染物排放成本G(t)的表达式为:

PG(t)(1-R)δGCG+PO(t)CO+
(8)

2)约束条件
约束条件包括光伏约束条件、机组特性约束、REH约束和系统约束,其中REH约束见式(1)至式(5)。
(9)
为了降低区域能源系统对于地区电网的影响,电力市场规定区域购电量在一定范围内,设定区域购电量浮动极限,即
0≤PR(t) (10) 根据机组特性,2台CHP和燃气锅炉电能出力上下限约束分别为: (11) 为进一步促进新能源消纳,考虑城镇与配电网的双向能量交互,以流入系统为正方向,城镇综合能源系统与配电网的联络线功率PLine约束可表示为: (12) 1)目标函数 (13) ∑L(t)=∑(Le(t)+Lh(t)) (14) ∑P(t)=∑(PR(t)+PP(t)+PB(t)+ PG(t)+PO(t)) (15) 式中:∑L(t)和∑P(t)分别为能量枢纽的总输出负荷和总输入能量。 2)约束条件 下层约束包括CHP机组补燃率约束,即 0≤A(t)≤Amax (16) 式中:Amax为内置补燃装置的最大补燃率。 结合式(1),本文调节CHP热电比的装置为内补燃装置,对于热电比的调节存在一定限制,故建立补燃约束如式(17)所示。 (17) 本文采取的差分改进帝国竞争算法[26]是一种基于帝国主义竞争机制的进化算法。微分进化算法具有实现简单、搜索能力强等优点;而帝国竞争算法具有全局收敛性强、可同时得到多个全局最优解等优点。综合上述优点,相比于一般的拉格朗日函数算法,避免了求取拉格朗日函数,对于本文这样下层优化目标复杂、约束较多的问题有较大优势。 基于文献[26]的改进差分帝国算法(DE-ICA),在同化操作和竞争操作之间添加微分变异和微分交叉操作,对本文的双层优化模型做以下处理后,作为算法输入量进行求解,具体算法执行过程如下。 1)初始化DE-ICA算法参数。初始化国家数量N、帝国数量M、同化系数β、偏移方向γ和殖民影响系数ξ。 2)决策变量编码。将上层决策变量天然气分配系数R(t)和生物质输入功率PB(t)作为决策变量按照调度时间进行编码: (18) 下层决策变量编码为天然气和生物质的两台CHP的热电比的组合: (19) 3)采用DE-ICA模型进行目标函数求解,并得出最终优化结果。优化过程如图3所示。 本文采用DE-ICA算法的具体参数如下:同化系数β=2,偏移方向γ=π/4,殖民影响系数ξ=0.1,变异因子F=0.5,交叉因子C=0.92,最大迭代次数Nn=200,国家数量N=100,帝国数量M=5。当层内分别用DE-ICA求解,过程中只剩一个帝国且该帝国及其殖民地拥有相同的优化变量和目标函数值时,即M=1且该帝国内各殖民地的决策变量Y相同,可认为该层收敛并得到最优解。当层间传递达到最大迭代数或连续20代双层优化结果未改进时,双层优化算法停止并输出双层最优结果。 算例模拟城镇典型的能源配置形式,考虑两台分别以天然气和生物质为燃料的CHP机组和一台以天然气为燃料的燃气锅炉。CHP最大电出力为0.4 MW,燃气锅炉最大输出热功率为1 MW。本地光伏和地区配电网也可提供电能,光伏采用某典型日数据,正午预测最大电功率为0.9 MW。 选用某地城镇地区某典型日真实热电负荷数据作为日前调度分析对象,时间尺度为1 h,热电负荷数据见附录A图A2。REH效率和优化模型中的部分参数如附录B表B1所示[24,27]。 对比研究3种不同的模式下的运行结果。3种模式说明如下。 模式1:城镇综合能源系统不使用生物质作为能量来源,仅考虑配电网、天然气、光伏和燃油作为能量来源,优化调度多种能源。 模式2:仅考虑生物质发电,该地区增加一台生物质微型燃气轮机,其他配置同模式1。 模式3:考虑生物质电热混合供能,配置余热锅炉收集生物质发电的剩余热量,其他配置同模式2。 应用本文第3节中的差分帝国竞争算法对上述双层优化问题进行求解,优化3种模式下能量集线器的输入向量P,结果如图4所示。本地电负荷无法消纳光伏发出的电量时,可在联络线功率的约束下向配电网供电。 图4 双层优化模型能量输入向量计算结果Fig.4 Calculation results of energy input vectors of bi-level optimization model 由上述结果可知,不使用生物质时(模式1),大量天然气用于燃气锅炉发电,天然气使用量较大,配电网功率取用量较大。对比模式2和模式3,由于生物质发电余热的回收大大提高了其能源利用效率,在下层优化中的竞争性显著增强,模式3中调度的生物质发电量增加,促进了当地生物质的规模化利用。 对比不加生物质、生物质单独发电以及生物质同时供电供热时的用能成本及能源利用效率,对比结果分别如图5(a)和(b)所示。光伏间歇性波动对电网储备容量提出了需求,研究发现生物质不同发电模式下的储备容量需求有所不同。图5(c)为反映电网储备容量需求大小的联络线调度功率。 图5 用能成本、效率和电网容量备用的对比Fig.5 Comparison of energy cost, efficiency, and grid capacity reserve 由图5(a)和(b)可知,随着可补燃生物质使用量的增加,模式3的用能费用和能效均显著优于模式2,由于生物质单独发电效率较低,模式2仅经济性略优于模式1。由此可见,单纯引入生物质发电对系统降低用能费用、提升能源利用率的效果有限。本文提出的生物质热电混合供能不仅提高了生物质在下层优化中的竞争性,增强了生物质的消纳能力(如附录A图A1所示),而且其在降低用能费用、提高整体能源利用效率方面也具有优越性。 由图5(c)可知,生物质热电混合供能模式下的电网最大储备容量需求为1.32 MW。因为模式2对系统优化的提升有限,模式1与模式2下的联络线功率相同,最大储备容量需求为1.48 MW。模式3相比前两种模式降低了12.12%,说明生物质参与且采用热电混合供能的模式可以明显降低区域综合能源系统对电网储备容量需求,在另一个层面也对降低能源费用起到了积极作用。 截取15:00—16:00的数据对模型上下层决策变量进行敏感性分析,共设计4个场景,结果如图6所示。 图6 敏感性分析Fig.6 Sensitivity analysis 场景1:天然气和生物质热电比皆固定为1.260 4,研究天然气分配比对成本的影响。 场景2:天然气和生物质热电比皆固定为1.260 4,研究生物质输入量对成本的影响。 场景3:生物质热电比固定为1.260 4,生物质输入量固定为500 kW。 场景4:天然气热电比固定为1.260 4,天然气输入量固定为500 kW。 上层模型包含两个优化变量,天然气分配比R(t)和生物质输入功率PB(t)。结合式(1)至式(5),将PB(t)看作定值,成本关于R的函数型为ax+1/(bx)+k;将R(t)看作定值,成本是关于PB(t)的一次函数。这二者的系数都会受下层优化变量的影响,因此存在着最佳天然气分配比使得成本最低,在最佳分配比之前,成本随分配比的增加而降低,最佳分配比之后成本随分配比的增加而增加。本文所选取的算例数据,受CHP机组容量的限制,系统中天然气分配比最大值在0.5以下,未达到ax+1/(bx)+k型函数的拐点。因此,图6(a)中,总成本关于R(t)呈现下降的趋势;又因为生物质能的成本比天然气的成本低,所以生物质能的用量越大,总成本就越低,即总成本与生物质输入量为负相关。 (20) (21) 本文针对生物质CHP加入补燃装置,构建生物质可补燃CHP机组模型,考虑天然气、光伏、配电网电能等多种能源,计及天然气可补燃CHP机组、变压器、燃气锅炉等多种能量转换设备,建立了多个不同输入能源的可补燃CHP的联合运行优化模型,提出了适用于城镇地区多种新能源高效消纳的综合能源运行双层优化方法。利用差分帝国竞争算法进行求解。构造城镇综合能源系统算例验证了生物质热电混合供能对能源效率和经济性都有改善作用。本文仍存在以下两方面不足:在能源输入侧,未能考虑风能、储能等实际中应用较广的新能源;在能源输出侧,未能考虑用户需求侧响应、电动汽车等可优化负荷。下一步将从上述角度进行研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

2.2 下层机组效率优化模型
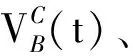
3 差分帝国竞争算法

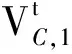

4 算例分析
4.1 基础数据
4.2 结果分析


4.3 敏感性分析

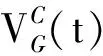
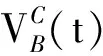
5 结语

