也论“单位涌水量就是导水系数”

尚银生，杨浪峰，梁 进(山西省勘察设计研究院，山西 太原 030013)

兰太权先生的《再论“单位涌水量就是导水系数”》[1](以下简称《再论》)刊于《水文地质工程地质》2016年第5期，通过井抽水理论要直接从达西定律出发、分析井抽水规律、试验证明等论述，根据“分析井抽水拦载径流量达到平衡态的稳定流特征，建立了渗透系数与井出水量、补给半径、水力坡度及含水层厚度之间的定量关系，进而推导出一个新的公式，发现‘单位涌水量就是导水系数’”。公式推导、观点几近类似的文章还有《井抽水地下水直线运动规律探讨》[2]等。只不过，前者直指裘布依公式为错误的径向流理论，建议改而采用所谓的新理论、新公式；后者则以期对裘布依微分方程的完善有所贡献。其实，水文地质研究者不仅考虑了假设地下水静水面为水平面的局限性，也为此进行了深入的探讨和分析。或许可以换个思路思考这一问题：是导水系数就是单位涌水量，还是利用的公式未能反映真实的水文地质条件、甚至错误；是导水系数影响着抽水试验的结果，还是所利用的抽水试验结果刻画的导水系数未能够、甚至不能与工程实际越来越接近。

1 地下水动力学中的因应之策

地下水动力学中的几个代表性理论如稳定流理论裘布依公式、非稳定流理论泰斯公式及考虑迟后疏干的博尔顿模型、考虑垂直分量和弹性释水的纽曼模型等，都有天然水力坡度为零或初始自由水面水平的假定。因此，《再论》的观点如若正确，则不仅否定裘布依公式，而且否定地下水动力学中的几个主要理论。

国内外水文地质研究者不仅从抽水试验方法中对观测孔的布置、观测孔的选用提出了相应的对策，而且在考虑地下水水力坡度不为零的情况下推导出繁简不同的计算公式。张宏仁先生编著的《地下水非稳定流理论的发展与应用》[3]中，摘译了温策尔的《确定含水介质渗透性的蒂姆法及其在确定给水度方面的应用》。其中的内布拉斯加州的抽水试验，目的层为潜水含水层，潜水水位埋深0.6～3.0 m ，大部分观测井井深介于1.9～8.2 m。抽水试验的主要目的是：寻找以抽水试验确定含水层渗透性可以采用的最好方法，以期从不那么复杂的抽水试验中获得满意效果。因为两次抽水试验计算出来的渗透系数变化范围很大，163.1～1 716.0 m /d，使得从这样的计算结果中确定最接近于正确的渗透系数成为几乎不可能的事。最终研究发现：对抽水井两侧相反方向、距离相等的观测降深取平均值，将趋于或等于这些距离上的理论降深，并以此来计算渗透系数，可以尽量减少蒂姆公式的误差；抽水开始后，抽水井附近降落漏斗较快达到实际上平衡的事实提供了利用蒂姆公式的机会。《供水水文地质手册》[4]给出了另外的建议：在天然水力坡度影响下，地下水等降深曲线不是以井轴为中心的同心圆，而是下游半径较上游半径为长的“似椭圆”，因而在圆周上布置观测孔所得的降深是角度θ的函数，即在上游得偏小值、在下游得偏大值，只有与天然水流垂直的方向上降深值无变化，因此，在此方向上布置观测孔、并用来求解水文地质参数较为合理。

前苏联学者恰尔內在考虑地下水三维流动，即以井距r处的潜水面水头代替裘布依圆柱面上的水头值，对Dupuit涌水量公式的正确性做了严格的解析证明，结果表明在考虑等水头线为曲线及水跃情况下(即非所谓的径向流情况下)，Dupuit涌水量公式仍然是正确的。其简证过程参见《地下水动力学》[5]。

施普德[6]在考虑天然水力坡度不为零的情况下，直接根据达西直线渗透定律，以极坐标原理、在一定的简化条件下导出潜水、承压水涌水量方程如下，并与裘布依公式进行了对比分析。

(2)

式中：H——天然水头高度/m；

Q——抽水井流量；

h0——抽水后井内水头高度/m；

K——渗透系数；

t——抽水时间;

r0——计算点到抽水井的距离；

n——沿地下水流向，下游影响半径与上游影响半径的比值；

R0——沿地下水流向，上游影响半径；

M——抽水井利用含水层的有效厚度；

r0——井半径。

初始自由水面不水平或天然水力坡度不为零的状况下，泰斯公式是否可以应用、该如何应用？文[5]有详细的论述与推导，提出了修正公式：

s=s1+s2

(3)

式中：s——初始水头非水平条件下，再加入一个定流量抽水井共同引起的水头降深；

s1——地下水天然动态降深；

s2——Theis井流降深。

2 关于《再论》推导的井抽水公式

文[1]推荐的井抽水公式及说明为：

(4)

式中：K——渗透系数；

Q——井抽水流量；

Rb——补给半径；

C——补给半径内进入抽水井的流量与全部流量的比例；

M——抽水井利用含水层的有效厚度；

I——地下天然水力坡度。

该式既不正确，也不便于直接用来计算渗透系数。它似乎为了便于演绎出所谓的导水系数与单位涌水量的关系而出现。

首先，公式中井抽水流量与天然水力坡度有关，而非与抽水过程中的地下水水力坡度有关，或者在表明：天然状态下，水力坡度一定时，在变更抽水量的情况下，渗透系数线性变化于抽水量。裘布依公式中，也有流量与渗透系数的关系式，但因应流量变化的主要参数之一是不断变化的水位降深。《再论》强调井抽水理论应该直接从达西定律这个基本规律出发，那么，利用达西定律在计算井周围侧向补给量时，应该利用抽水状态下的地下水水力坡度。

《再论》通过分析井抽水规律、进行试验证明，得出所谓的新论断：单位涌水量就是导水系数。既然水位降深是一个关键的参量，更为重要的是可以方便的直接测量出，但上述式(4)中并不包括。

3 对Rb、C进一步分析

《再论》未详细提及Rb的来源，但文[7]中提到：考虑天然水力坡度的情况下，抽水后抽水井下游的水力坡度为:

(5)

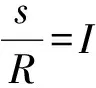
(6)

这种推导过程存在问题：(1)与其考虑随着影响半径R的增大，下游静水面到抽水井动水面的水力坡度逐渐减小，还不如认为随着降深的增大、影响半径也增大更为合理。(2)此时井下游的水力坡度为零，不存在所谓的补给半径。(3)影响半径不是渗透途径，计算水力坡度时，除以影响半径显然不符合水力坡度的定义。按此计算已然忽略了地下水流速的垂直分量，或者说同裘布依假定一样，同样忽略了地下水的垂直分量。《再论》强调天然状态下很小的水力坡度都要明确考虑、加以利用，对水力坡度也有明确的认识，但却对抽水试验中存在较大的水力坡度计算时反而以径向距离代替渗透路径来计算，在所谓的井抽水公式中利用天然水力坡度、而不用抽水状态下实际水力坡度。

4 关于试验证明

《再论》提及的试验验证见于文[7]，即建造一个承压含水层试验装置，随后另在铁皮箱进行了相关的试验，以此进行抽水试验并进行相关参数计算。这些试验证明也有问题。首先，以试验宽度与含水层厚度之积作为过水断面，用以计算的是地下水侧向补给量，并不能代表抽水井涌水量的大小。其次，文[7]根据达西定律反算渗透系数时，利用的是不同抽水量状态下相应的水力坡度，而所推荐的井抽水公式利用的是天然水力坡度，亦即单位涌水量计算中，包含的是天然水力坡度的影响，而在反算渗透系数时利用变化的水力坡度、而非天然或初始水力坡度。此外，这些仅在承压含水层中的试验，其水流基本为径向水平流，不能证明所谓的观点(尽管这些观点源于温策尔的潜水抽水试验中分水点的启发)在潜水含水层也是合理的。

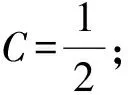
5 结论