安哥拉Quelo砂场地非饱和渗流试验与计算

刘争宏，王华山，周远强，唐国艺，于永堂，刘 智(1.长安大学地质工程与测绘学院，陕西 西安 71005； 2.机械工业勘察设计研究院有限公司，陕西 西安 71003；3.陕西省特殊岩土性质与处理技术重点实验室，陕西 西安 71003; .中国机械设备工程股份有限公司，北京 100037)

目前，对非饱和土渗流特性的研究主要采用试验法[1～2]、解析法[3]和数值法[4～5]等方法。试验法结果较为准确、直接，被工程界广泛认可与接受，但实施较为麻烦，试验工况一般较少。解析法一般仅适用于边界条件简单、渗流域规则的渗流问题。数值法实施简单，结果丰富，但往往与实际存在差别，需要合理校正。若能将试验法(特别是现场大型试验)和数值法结合起来，并在对比基础上积累数值法的计算经验，使数值法更接近试验法结果，对今后使用数值法解决实际工程问题具有重要价值。目前，国内学者已对室内模型试验与数值法[6～7]，以及降雨条件下现场试验与数值法[7]进行了对比研究，但鲜有大型现场浸水试验与数值法结果对比研究的报道。

近年来，中国越来越多的工程企业走出国门，开拓海外市场，在这个过程经常会遇到一些特殊土问题。例如，在非洲国家安哥拉首府罗安达及其周边的浅部地层中，广泛分布着一种棕红色粉砂，在当地被称为Quelo砂或Muceque砂，当地大量建(构)筑物将其作为基础持力层[8]。Quelo砂的黏粒含量高、水敏性强，属于典型的非饱和特殊土，与一般粉砂的工程性质差异明显。目前国内学者对Quelo砂的湿陷性、抗剪强度特性、承载性状、压实特性等[8～12]开展了一些研究工作，但针对其渗流特性的现场试验和数值模拟研究成果鲜见报道。

由于工程需要，在非洲国家安哥拉Quelo砂场地开展了大型现场试坑浸水试验，监测了水的入渗和消散过程，同时也测得了数值法渗流计算所需要的主要土性参数。基于测试结果，开展了数值法与试验法结果的对比研究工作，并提出了能较好反映实际情况的数值计算经验方法。以期为更好地使用数值法解决类似工程问题做出些许贡献。

1 现场试坑浸水试验

1.1 场地条件

本次现场试坑浸水试验在非洲西部国家安哥拉首都罗安达省KILAMBA KIAXIA地区进行。场地地貌为构造剥蚀平原，地势平坦，地下水稳定水位埋藏深(埋深超过80 m)。试验场地地层特征如表1所示，上部为粉砂层(包括②、③1和③2)，下部为泥岩，其中粉砂②层和粉砂③1层具湿陷性[13]。室内试验得到各土层土性指标(均值)如表2所示，其中粉砂②层和③1层饱和渗透系数较大，粉砂③2层和泥岩④层渗透系数较小，总体有随深度增加渗透系数减小的规律。采用筛分法和密度计法相结合的颗粒分析试验得到砂土层粒径级配曲线如图1所示。

表1 试验场地地层特征Table 1 Characteristics of the test site

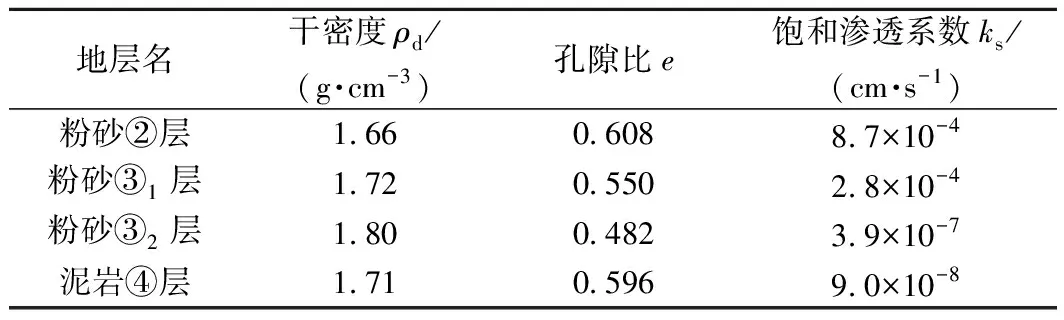
表2 地层基本指标Table 2 Basic parameters of the soil layers

图1 地层颗粒分析级配曲线Fig.1 Gradation curves of stratigraphic analyses in strata

1.2 试验方法与过程

现场试坑浸水试验采用圆形试坑，直径16 m，深度0.5 m，试坑底部铺设0.1 m厚碎石，试验坑内设置有标点观测地基土的沉降。浸水试验共注水10 d，总计注水量为3 020 m3，单天注水量如图2所示。采用水车拉水与市政自来水相组合的方式供水，由于当地自来水经常停水以及考虑安全因素夜晚水车不宜工作，有部分时段试坑中处于无水状态(图5)。根据当地年蒸发量数据估算，蒸发量相对于注水量的占比不超过0.5%，可忽略水分蒸发对分析结果的影响。试验过程中粉砂②层、③1和③2层均未发生显著变形。

图2 试验单天注水量Fig.2 Single-day water injection of the test

为监测水的渗流过程，在试坑内外布设了30个土壤水分计(图3)。试坑内土壤水分计布置在以试坑中心为圆心、半径7 m的圆周上，布设深度自坑底面以下2～12 m，每间隔2 m布设1个，共计6个；试坑外共集中布设4排，深度自坑底面标高以下2～8 m，水分计相邻标点距试坑中心的距离差为1.5 m，离试坑最近水分计距试坑边沿1.5 m。按轴对称问题考虑(对称轴为经过试坑中心的垂线)，土壤水分计在竖向的等效布设效果如图4所示。水分计在钻孔底中埋设，采取了夯实回填以及间隔一定距离回填水泥砂浆的隔水措施，确保钻孔不成为渗水通道，水分计能真实反映水的入渗情况。在测试数据处理时，根据浸水前、浸水后2组土壤水分计测试值与烘干法含水率(传感器埋设位置附近钻孔取土)测试值建立现场标定公式修正土壤水分计测试值，浸水时采用土壤水分计连续观测土层含水率变化；由水浸湿到各土壤水分计测点引起的测试值突变时间确定各测点位置土层遭水浸湿的时间，进而得到不同浸水试验时间土层的浸润过程及范围。试验所用器材和仪器设备均从国内海运至现场。

图3 土壤水分计平面布置图Fig.3 Layout of the soil moisture meters

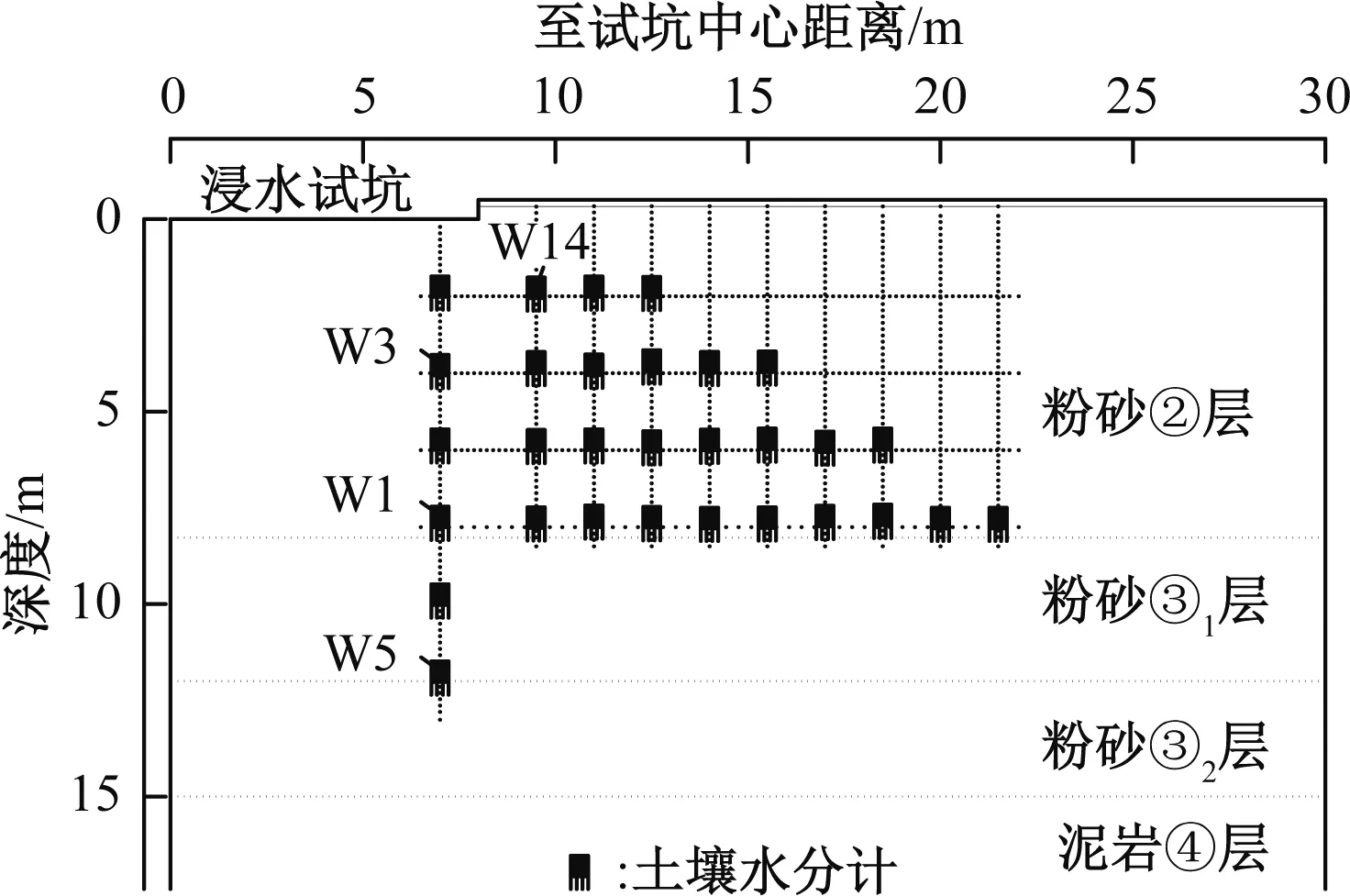
图4 土壤水分计布设深度Fig.4 Designed depth of the soil water meters

图5为试坑内4 m深度(编号W3)和8 m深度(编号W1)土壤水分计的实测体积含水率(实测读数代入水分计标定公式计算得到的值)历时曲线，从中可以清晰地分析出土壤水分计埋设位置受水浸湿的起始时间。分析各土壤水分计位置的浸润时间，可获得试验过程中水的浸润过程。停水后，随着水分消散，部分水分计读数降低，也可以反映水的消散过程(如试验后期W3和W1水分计在试验历时12天和28天时含水率也开始了下降)。

图5 土壤水分计测试历时曲线Fig.5 Diachronic curves of the measured water content by the soil water meters

在试坑外还布设了5个水位观测孔，观测试验过程中自由水面的变化过程，水位观测孔沿半径方向间隔2 m在距试坑边沿2～10 m范围内布设。

2 渗流数值计算

本次计算选用Geo-Studio软件SEEP/W模块进行现场试验的渗流分析。Geo-Studio是GEO-SLOPE国际公司开发的数值分析软件，其中的SEEP/W模块可用于非饱和土渗流计算。

2.1 计算原理

研究表明，达西定律不仅在饱和土渗流中运用，而且也可运用于非饱和土渗流中。区别在于不饱和渗流的条件下渗透系数是变量，随含水率变化，即：

(1)

式中：v——渗流速度；

h——总水头；

θw——体积含水率；

k(θw)——渗透系数；

二维渗流一般控制微分方程为：

(2)

式中：kx，kz——x方向、z方向渗透系数；

Q——施加边界流量；

t——时间。

体积含水率的变化取决于应力状态的改变和土体性质。Fredlund和Morgenstern[14～15]提出非饱和条件下的体积含水率与(σ-ua)和(ua-uw)呈函数关系，即：

dθw=-mσd(σ-ua)-mwd(ua-uw)

(3)

式中：mσ——与法向应力(σ-ua)相关的体积变化曲线斜率；

σ——总应力；

ua，uw——孔隙气压力和水压力；

mw——与基质吸力(ua-uw)相关的体积变化曲线斜率，为土-水特征曲线斜率。

瞬态问题中，假定没有土体的卸载和加载，非饱和区孔隙气压不变，则有：

(4)

式(2)可转化为：

(5)

式(5)即为控制方程，是SEEP/W有限元程序的计算基础[16]，其求解需要知道土的土-水特征曲线和渗透系数函数。

2.2 土-水特征曲线

本次计算采用改进的Kovács粒径方法估计砂土层的土-水特征曲线，模型定义如下[17]：

(6)

式中：Sr——饱和度；

θw——体积含水率；

n——孔隙率；

Sc——毛细饱和度；

Sa*——界限黏附饱和度。

毛细饱和度Sc可由下式确定：

Sc=1-[(hco/ψ)2+1]mexp[-m(hco/ψ)2](7)

(8)

ζ≈402.2 cm2

(9)

式中：hco——等效毛细管上升高度；

ψ——基质吸力；

m——拟合参数(常数)；

e——孔隙率；

D10——土级配曲线中含量10%对应粒径；

wL——液限；

Cu——不均匀系数。

(10)

式中：Sa——黏附饱和度，由下式确定：

(11)

(12)

式中：a——拟合参数(常数)；

ψn——归一化参数；

CΨ——校正因子；

ψr——残余含水率下的基质吸力。

SEEP/W程序中只要求输入土粒径分布曲线上小于该粒径的土含量占总土质量的10%和60%的粒径(有效粒径和限制粒径，按图1取值)，以及饱和体积含水率就可估计出砂土的土水特征曲线。值得注意的是，如图5所示的实测体积含水率，其最大值并未对应100%饱和度，表明即使大面积浸水条件下，地基土也难以达到100%饱和度，分析实测体积含水率，本试验试坑内砂土②层达到的饱和度平均值约为70%(如图4中W3、W1和W5的饱和度测试值分别为70%、62%和72%)，所以本次计算将对应饱和度Sr分别为70%和100%的体积含水率作为“饱和体积含水率”(表3)进行了计算，以研究“饱和体积含水率”参数对计算结果的影响。初始体积含水率采用室内实验测得。

表3 土-水特征曲线所需参数Table 3 Parameters for soil-water characteristic curve

本文主要研究砂土层的渗透特性，其下泥岩层主要成分是黏土，采用软件自带的黏土样本函数拟合泥岩土-水特征曲线。根据输入参数软件自动获得的土-水特征曲线见图6(仅展示对应饱和度70%作为“饱和体积含水率”的结果)。

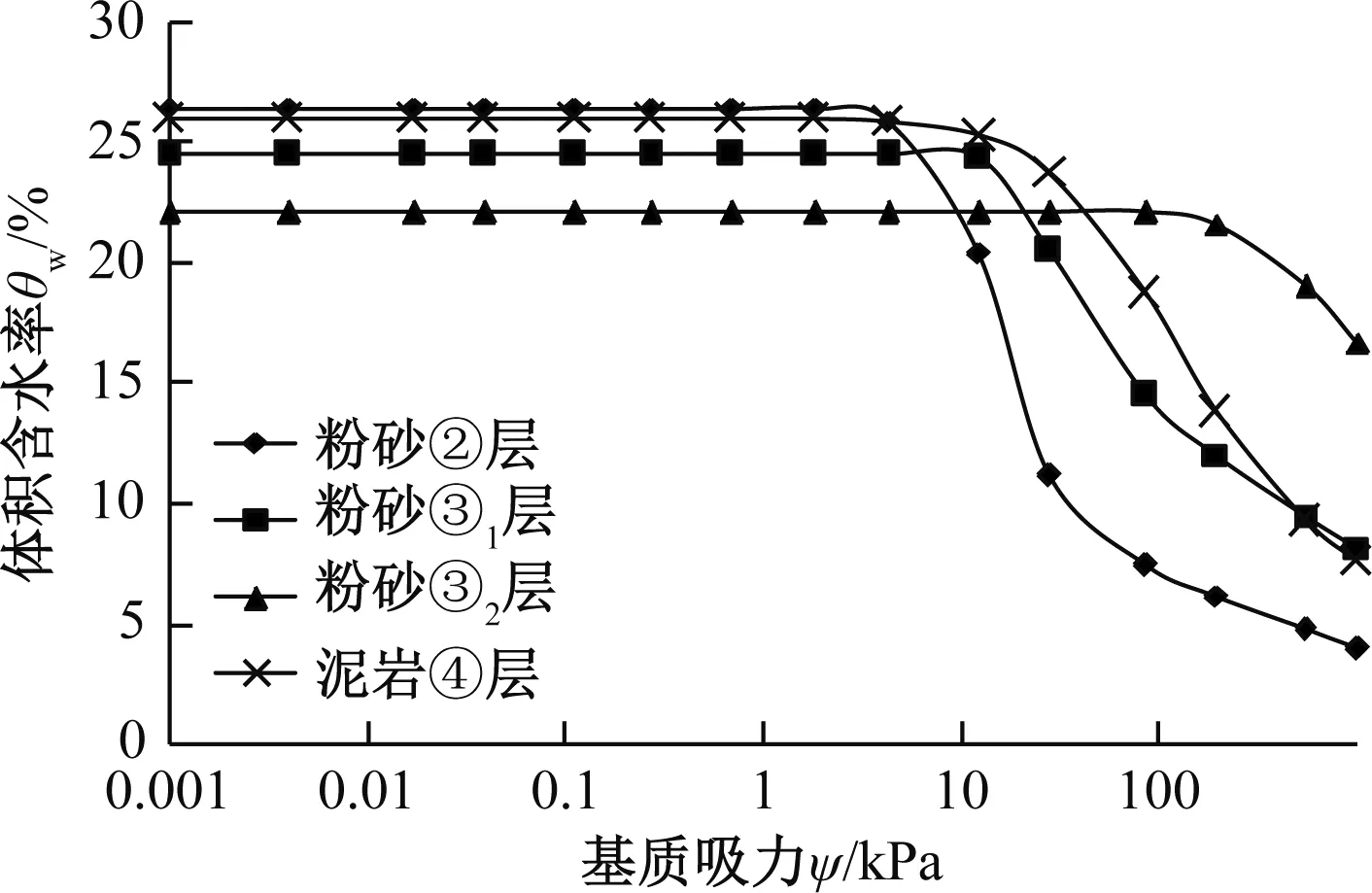
图6 各土层土-水特征曲线Fig.6 Soil-water characteristic curve in each stratum

2.3 渗透系数函数

本文选用Van Genuchen模型方法估算各地层的非饱和土渗透系数曲线。Van Genuchen模型[18]基于土-水特征曲线获得，可由下式表示：

(13)

式中：ks——饱和渗透系数；

α，m，n——曲线拟合参数(m=1-1/n)。

渗透系数拟合参数最佳拟合点在体积含水量函数的残余含水量和饱和含水量之间。体积含水率函数斜率计算式为：

(14)

式中：Sp——体积含水率函数斜率；

θs——饱和体积含水率；

θr——残余体积含水率；

θp——体积函数率函数的中点体积含水率；

ψp——p点的基质吸力。

则参数α，m可用下式计算：

(15)

(16)

本次计算饱和渗透系数按表2所示室内试验(常水头试验法)实测值取值，残余体积含水率参照文献[19]取值：砂土取0.08，泥岩取0.15。其中对应图6的渗透系数函数曲线如图7所示。

图7 各土层渗透系数与基质吸力关系曲线Fig.7 Relationship between the coefficient of permeability and matrix suction in each stratum

2.4 计算模型

假定每一层地层均匀，且水力学性质相同，地表土采用粉砂②层代替。取通过浸水试坑中心且与试坑水平面垂直的剖面为计算模型，该问题为轴对称问题，以浸水试坑底中心为坐标原点，径向为横轴正方向，竖直向上为纵轴正方向。模型尺寸(宽×深)为60 m×20 m，有限元网格图如图8所示。

图8 有限元网格Fig.8 Finite element grid

浸水试坑范围内为入渗边界，注水流量和时间按图2(单天水量)及图5(试坑中有水时间)控制；模型上部的其它部位、两侧、底部均假设为不透水边界。

3 实测与计算结果对比

通过对比浸水过程中的浸润范围以及停水后水的消散快慢(含水率)来衡量计算效果。

3.1 浸润范围对比

如图9所示为浸水过程中浸润范围的对比，其中的实测浸润线根据土壤水分计测试结果绘制，浸润线以左(试坑一侧)地基土受到了水的浸润作用，含水率有增大；实测水位线根据水位观测孔的实测水面埋深绘制。与实测浸润线和水位线相对应，也可按数值计算结果绘制出计算得到的浸润线和水位线，其中浸润线为含水率发生变化的边界线，水位线为孔隙水压力为0的等值线。图9中“Sr=70%”和“Sr=100%”分别表示将饱和度Sr为70%和100%的体积含水率作为“饱和体积含水率”(分别将饱和度70%和100%视作饱和，以下分别简称“70%饱和计算”和“100%饱和计算”)输入得到的计算结果。

图9 实测与计算浸润范围对比Fig.9 Comparison of the measured and calculated infiltration areas

从图9中可以看出，数值计算结果正确展现了砂土浸水后宏观上先以向下渗透为主，再向四周扩张的过程。但更细致分析可发现，实测与计算结果存在一定差别，从“100%饱和计算”结果，到“70%饱和计算”结果，再到实测结果，浸润线和水位线的斜率(线与水平面夹角的正切)越来越小，水的浸润范围越来越大。以与实测结果的差异大小作为计算优劣的评判标准，则“70%饱和计算”要优于“100%饱和计算”，即在数值法中，若饱和体积含水率按100%饱和度对应的体积含水率输入，将产生较大的误差。但即使饱和体积含水率按试坑内浸水达到的平均饱和度70%输入参数，实测的浸水范围也更大，探究其原因在于试坑外实测和计算的饱和度仍存在差异，数值计算结果当中，“水位线”以内(试坑一侧)土的饱和度都将达到最大饱和度70%，而实际上试坑外“水位线”以下土的最大饱和并度未达到70%，实测饱和度为45%～69%，且不同位置地基土饱和度具有差异，存在“上小下大，外小里大”的规律，饱和度平均值为58%，上述差异导致了计算得到的浸润范围要小于实测结果。站在工程的角度思考问题，试验场地的粉砂②层和③1层为湿陷性土，在低含水率条件下具有较大的抗剪强度指标和湿陷系数[8，13]，但当它们的饱和度增加到58%后(离100%饱和度还很远)，湿陷性和增湿软化的特性也消失殆尽；而“70%饱和计算”得到的浸润范围比实测的小，用此指导工程实践将偏于不安全。要使采用数值法得到的浸润范围和实际差别不大，或者说能指导工程实践，应开展和本文相类似的对比研究，找出地区计算渗透范围的“经验饱和体积含水率”取值方法，通过试算，若将本文数值计算中饱和体积含水率取65%饱和度对应的体积含水率，可使得浸润线计算值与实测值接近，取50%饱和度对应的体积含水率，可使水位线计算值与实测值接近。

3.2 含水率对比

图10为“70%饱和计算”得到的W14和W3传感器位置土的体积含水率历时曲线与实测结果。

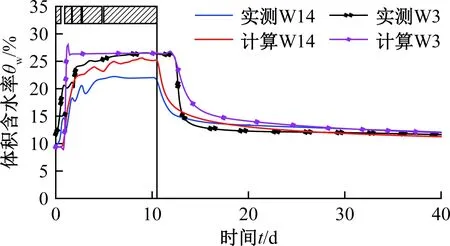
图10 实测与计算体积含水率对比曲线Fig.10 Comparison curves of the measured and calculated volumetric water content

从图10中可以看出，数值计算结果较好地反映了土的体积含水率开始回落时间，W14位置位于试坑外距试坑边沿1.5 m处，相对于试坑底面标高的埋深为2 m，在试坑内没有水源补给后土的含水率很快开始了回落，W3位于试坑内，相对于试坑底面埋深为4 m，在停水后2d含水率开始回落，且当时间足够长时，计算和实测含水率趋于一致，不管是W14位置还是W3位置，其体积含水率均在12%附近，反映了粉砂②层地基土较差的保水能力。但从含水率减小的速度来看，计算得到的减小速度相对实测更慢，从工程实践角度来看计算结果偏于安全，且误差可接受，即可用数值法预测停水后水的消散过程。

4 结论

(1)现场试坑浸水试验实测浸水后试坑内砂土的平均饱和度约70%，试坑外自由水面下砂土的平均饱和度为58%，远未达到完全饱和(饱和度100%)。由于场地下部存在相对隔水层，水的宏观渗透规律为先以向下渗透为主，然后逐渐向四周扩张。

(2)通过室内实测土的级配曲线和饱和渗透系数，使用改进的Kovács粒径方法估计砂土层的土-水特征曲线，Van Genuchen模型估算非饱和土的渗透系数曲线，采用数值计算方法可模拟出水在砂土中与实际相同的宏观渗透规律。

(3)由于浸水条件下非饱和土难以达到完全饱和，因此输入对应饱和度100%的“饱和体积含水率”进行渗透计算会严重低估水在地基土中的渗透范围。为较准确模拟水在地基土中的渗透范围，应开展实测与计算的对比试验，确定地区合适的“饱和体积含水率”取值方法，本文场地合适的“饱和体积含水率”对应饱和度为65%。

(4)数值计算结果较好地反映了本次试验场地停水后地基土含水率开始减小的起始时间，水消散后地基土含水率也与实测结果接近，但数值计算得到的水消散速度要比实际稍慢。