孔径分布对软黏土渗透特性的影响分析

金 盼，陈 波，胡云世(衢州学院建筑工程学院，浙江 衢州 324000)

土体渗透性是指水通过土体孔隙的能力，可通过渗透系数来表征土体的渗透性能。渗透系数作为软黏土地区工程设计的一个重要控制参数，直接影响建筑物和填方路堤沉降时间、基坑开挖过程中降水井布置、污染物防渗层厚度设计和计算[1～2]。因此，软黏土渗透系数的试验测定、影响因素分析和经验模型建立等方面也一直是研究人员关注的重点。

目前，国内外学者基于软黏土在不同固结压力下的渗透试验结果，得出渗透系数与软黏土的含水量[3～5]、孔隙比[6～8]、塑性指数[9～10]、结构性[11～13]等因素密切相关，并在深入分析渗透系数kv随孔隙比e变化规律的基础上提出相应的预测模型，如：软黏土中较常见的e-lgkv模型[3,12]和改进的lg(1+e)-lgkv模型[11]等。尤其是软黏土的结构性，作为与初始孔隙比和应力历史同等重要的参数，其对软黏土的力学特性具有重要影响，并取得了丰富的研究成果[14～15]。相比于结构性对软黏土变形和强度特性影响的研究成果，结构性对软黏土渗透特性影响的研究成果则相对较少，且主要集中于通过比较同一固结压力或同一孔隙比下, 软黏土原状样和重塑样的渗透系数差异来说明结构性对土的渗透特性的影响。然而，对于结构性导致原状样和重塑样渗透系数存在差异的内在机理，尤其是基于土体孔径大小及分布等微观结构的分析与研究，研究成果更为有限。因此，有必要在开展宏观试验的基础上分析软黏土原状样和重塑样微细观结构的差异，探究结构性影响软黏土渗透特性的微细观机理。

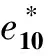
1 试验土样及方法

1.1 试验土样

原状样：试验的三种土样分别为取自上海的川沙、浦东和江苏的宝应地区，其中，上海川沙软黏土采用的是扰动程度较大的厚壁取样方式获得，取自地表以下约7.0 m处，上海浦东和江苏宝应软黏土则采用扰动程度最小的块状取样方式获得，分别取自地表以下约1.5 m和9.8 m处。试验土样的基本物理特性、颗粒大小组成详见表1。

表1 试验土样的基本物理特性Table 1 Basic physical properties of soil samples

重塑样：用纯净水将现场取来的软黏土充分浸泡后搅拌均匀，配制成初始含水量约为2倍土体液限的饱和泥浆，倒入直径为15 cm、高度为16 cm的大型固结容器后分级加载，使其固结成样，试样的最后一级荷载约为70 kPa。固结完成的重塑样用多层保鲜膜包好并蜡封后储存在密闭容器中，并根据需要切取其中一部分制成试验用的试样。该制样方式虽然使重塑样的含水率和结构性与原状样存在较大差异，但由于试样具有均匀性好、可重复强的优点，且可通过比较相同孔隙比情况下的渗透系数消除含水量差异产生的影响。同时，该制样方式虽然改变土体结构中的组构部分，但并不会使重塑样产生胶结作用，且本文重点分析的是相同孔隙比下，土体孔径大小及分布(组构)对土体渗透性产生的影响。因此，可采用上述方法进行重塑样的制备。

1.2 试验方法

本次试验采用间接法测定土的渗透系数。即，通过记录固结试样在各级荷载作用下6 s、15 s、60 s、135 s、240 s、375 s、540 s、735 s、960 s、…的变形量，得到试样在各级荷载下的固结曲线，确定t90后得到该级压力下的固结系数Cv，并利用式(1)间接求得土体在相应固结压力下的渗透系数：

k=Cvavγw/(1+e1)

(1)

式中：k——渗透系数；

Cv——固结系数；

av——前一级压力与本级压力区段下的压缩系数；

e1——前一级压力下的孔隙比；

γw——水的重度。

1.3 土样结构性分析

图1为根据不同试样在各级压力下24 h的稳定变形量后得到的压缩曲线，其中，U表示原状样的试验结果，R表示重塑样的试验结果，以下类同。从图1中可以看出，用块状取样方式得到的宝应和浦东软黏土原状样的压缩曲线的结构屈服较为明显，而采用厚壁取样方式得到的川沙软黏土原状样的压缩曲线则结构屈服不明显，说明采用块状取样方式得到的原状样质量明显优于厚壁取样方式得到的原状样的质量。

图1 不同软黏土的e-lgσv曲线Fig.1 e-lgσv curves of different soft clays

(2)

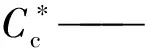
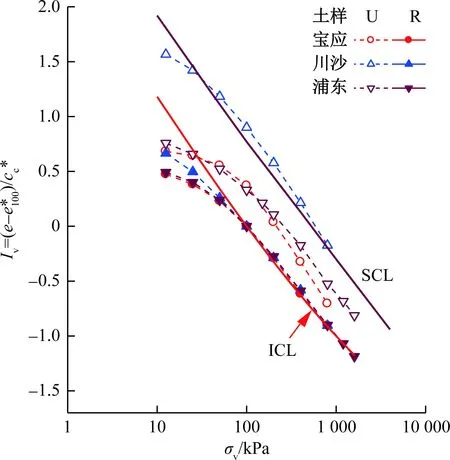
图2 不同软黏土的归一化压缩曲线Fig.2 Normalized compression curves of different soft clays

2 试验结果

2.1 渗透系数随固结压力变化规律

图3为试验得到的不同软黏土原状样和重塑样的渗透系数kv随固结压力变化的lgkv-lgσv曲线。图3表明：无论是原状样还是重塑样，土样的渗透系数均随着固结压力的增大而逐渐减小，且原状样的渗透系数在结构屈服应力前后具有明显的突变现象，即，结构屈服应力前，土体的渗透系数随固结压力的变化较小，结构屈服应力后，土体的渗透系数随固结压力变化明显增大，与孙德安等[12]的试验结果一致；与川沙软黏土相比，采用块状取样得到的浦东和宝应软黏土原状样的渗透系数在结构屈服应力附近发生陡降的现象更加明显，说明原状样的取样质量对土体渗透系数的变化规律也具有重要影响。需要注意的是，本试验得到的重塑样渗透系数也存在不同程度的突变，与一般的试验结果不同[11～12]，这主要是试验用的重塑样受过70 kPa的前期固结应力导致的，且该前期固结应力与渗透系数突变点处的应力基本一致。

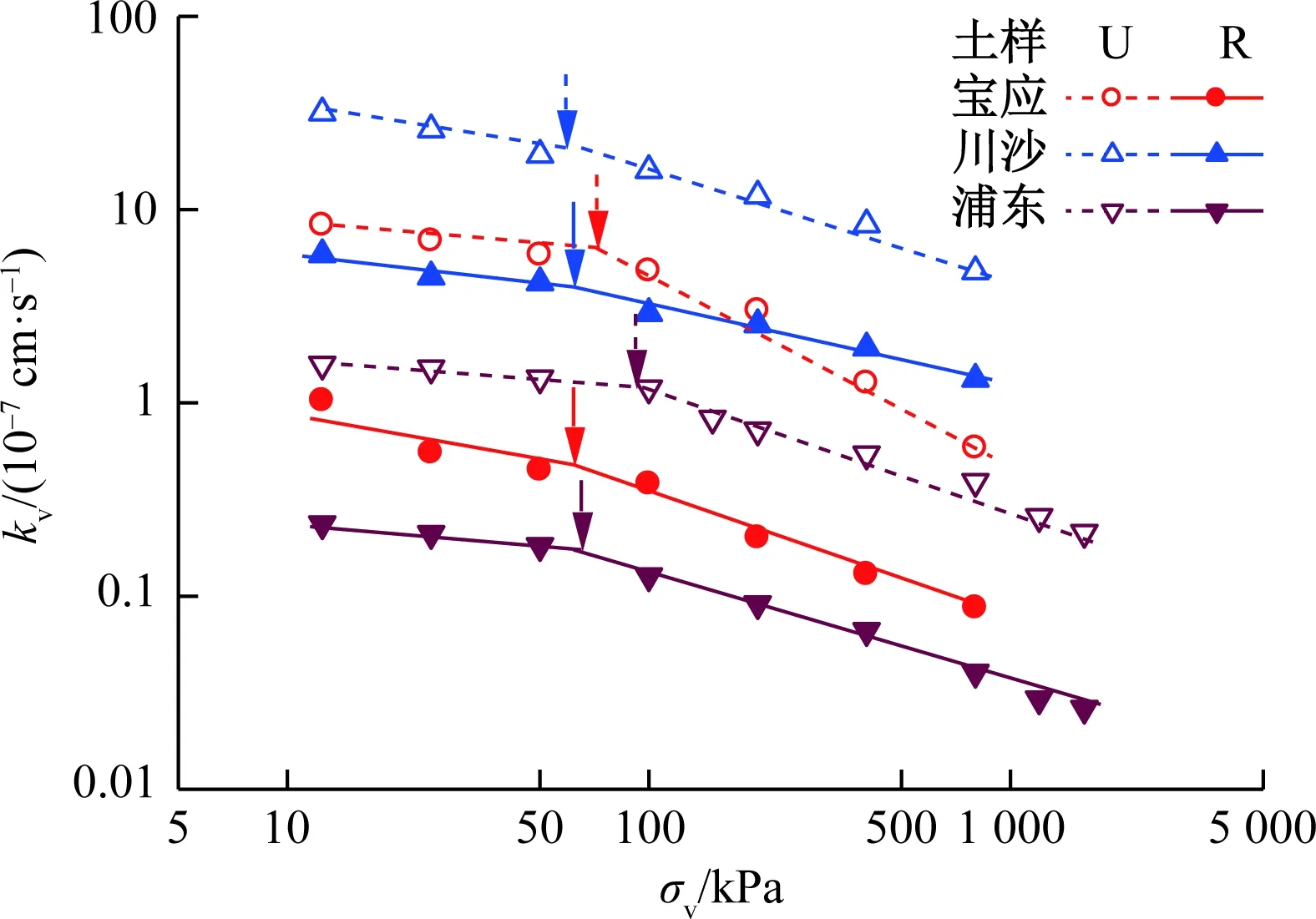
图3 不同软黏土的lgkv-lgσv曲线Fig.3 lgkv-lgσvcurve of different soft clays

图3还显示，3种不同软黏土原状样lgkv-lgσv曲线均位于相应重塑样的上方，且两者的差距随固结压力的增大而减小，说明在同一固结压力下，原状样的渗透系数明显地大于相应重塑样的渗透系数，且随着固结压力的增大，原状样与重塑样在相同压力下的渗透系数差距逐渐减小。此外，不同土样在同一应力水平下的渗透系数的差距也极大，且最大可达数十倍，一方面是由于同一应力水平下不同软黏土的孔隙比存在较大的差距，如图1中所示的川沙和宝应软黏土重塑样，它们在初始固结应力条件下的孔隙比差值达到0.25左右；另一方面则是由于不同软黏土的颗粒级配存在较大的差异引起的，如图3中所示的浦东和宝应软黏土重塑样，虽然它们具有相同初始孔隙比，但它们的渗透系数也具有明显的差异。

2.2 渗透系数随孔隙比变化规律

为分析土体结构性这一因素对软黏土渗透系数的影响，需要比较不同软黏土原状样和重塑样在相同孔隙比下渗透系数的差异，从而消除孔隙比不同对土体渗透系数产生的影响。作者将试验结果进一步整理后，得到图4所示的不同软黏土的原状样和重塑样的渗透系数kv随孔隙比变化的e-lgkv曲线。

图4 不同软黏土的e-lgkv曲线Fig.4 e-lgkv curves of different soft clays

图4表明，无论是原状样还是重塑样，软黏土的渗透系数均随着孔隙比的减小而逐渐减小，且两者的变化模式也基本相同，在e-lgkv坐标系中为一条直线，与众多的试验结果一致[11～13]。不同软黏土原状样的渗透系数与孔隙比的变化模式在屈服前后基本一致，且也与重塑样大致相同，说明软黏土原状样的渗透系数主要受土体的孔隙比影响，与土体结构的胶结结构关系不大。同时，从图4中可以看出，不同软黏土原状样的e-lgkv曲线均位于相应重塑样的右侧，说明在相同孔隙比时，软黏土原状样中存在的结构性将使其渗透系数明显大于相应重塑样的渗透系数。众多试验结果表明，软黏土结构性的胶结结构对软黏土渗透系数影响不大，但孔隙结构和大小对土体的渗透系数具有重要影响[6,9,13]，因此，可认为软黏土原状样和重塑样渗透系数的差异主要是由土样的孔径大小及分布引起的，即，土体结构中的组构导致的。

3 渗透系数影响因素

3.1 颗粒级配对渗透系数的影响

图4还表明，不同软黏土在相同孔隙比下的渗透系数也存在不小的差距，即便是采用同一制样方式得到的重塑样，这主要是由于不同土体的颗粒级配不同引起的。从图4中可知，在同一孔隙比下，浦东软黏土重塑样的渗透系数小于宝应软黏土重塑样的渗透系数，且都明显地小于川沙软黏土重塑样的渗透系数。考虑到上海浦东和川沙软黏土的相关物理指标较为接近，因此，可认为这主要是颗粒级配差异导致两者渗透系数的差异。

为详细分析颗粒级配对土体渗透性的影响，作者参照张先伟等[16]分类方法将软黏土颗粒级配曲线进一步细分为砂粒(>0.05 mm)、粉粒(0.005～0.05 mm)、黏粒(0.002～0.005 mm)和胶粒(0.002～0.005 mm)，相应的比例见表1。从表1中可以看出，川沙软黏土中的砂粒颗粒含量高达7.2%，明显多于另外两种软黏土的砂粒颗粒含量；同理，宝应软黏土的砂粒颗粒含量也多于浦东软黏土的砂粒含量，考虑到粗颗粒含量对土体渗透特性具有重要的影响，因此，可从软黏土的砂粒含量方面合理地解释同一孔隙比下川沙软黏土的渗透系数最大、浦东软黏土的渗透系数最小的原因。

3.2 孔径分布对渗透系数的影响

由于影响土体渗透系数大小的主要因素为孔径大小和分布，即土体结构中的组构，已有试验结果表明，原状样和重塑样的孔径大小及分布等微观结构存在明显的差异[17]。因此，对相近孔隙比下的浦东软黏土原状样和重塑样开展压汞试验测得的孔径分布曲线进行比较，分析孔径大小及分布对软黏土渗透特性的影响，试验详细情况见表2。

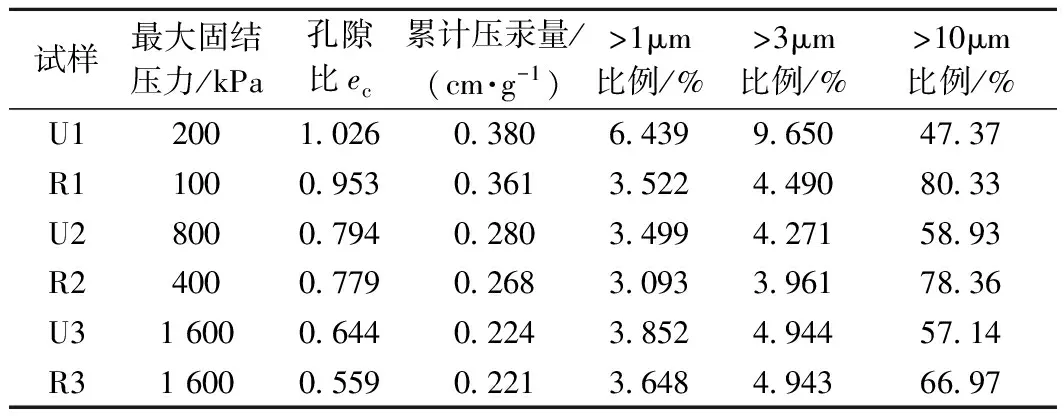
表2 累积汞压入量相近的不同土样孔隙比及对应固结应力Table 2 Consolidation pressure and void ratio of different samples with a close cumulative intrusion volume of mercury

图5 孔隙比相近的原状样和重塑样的孔径分布密度Fig.5 Pore-size distribution density of the undisturbed and reconstituted samples at the same void ratio

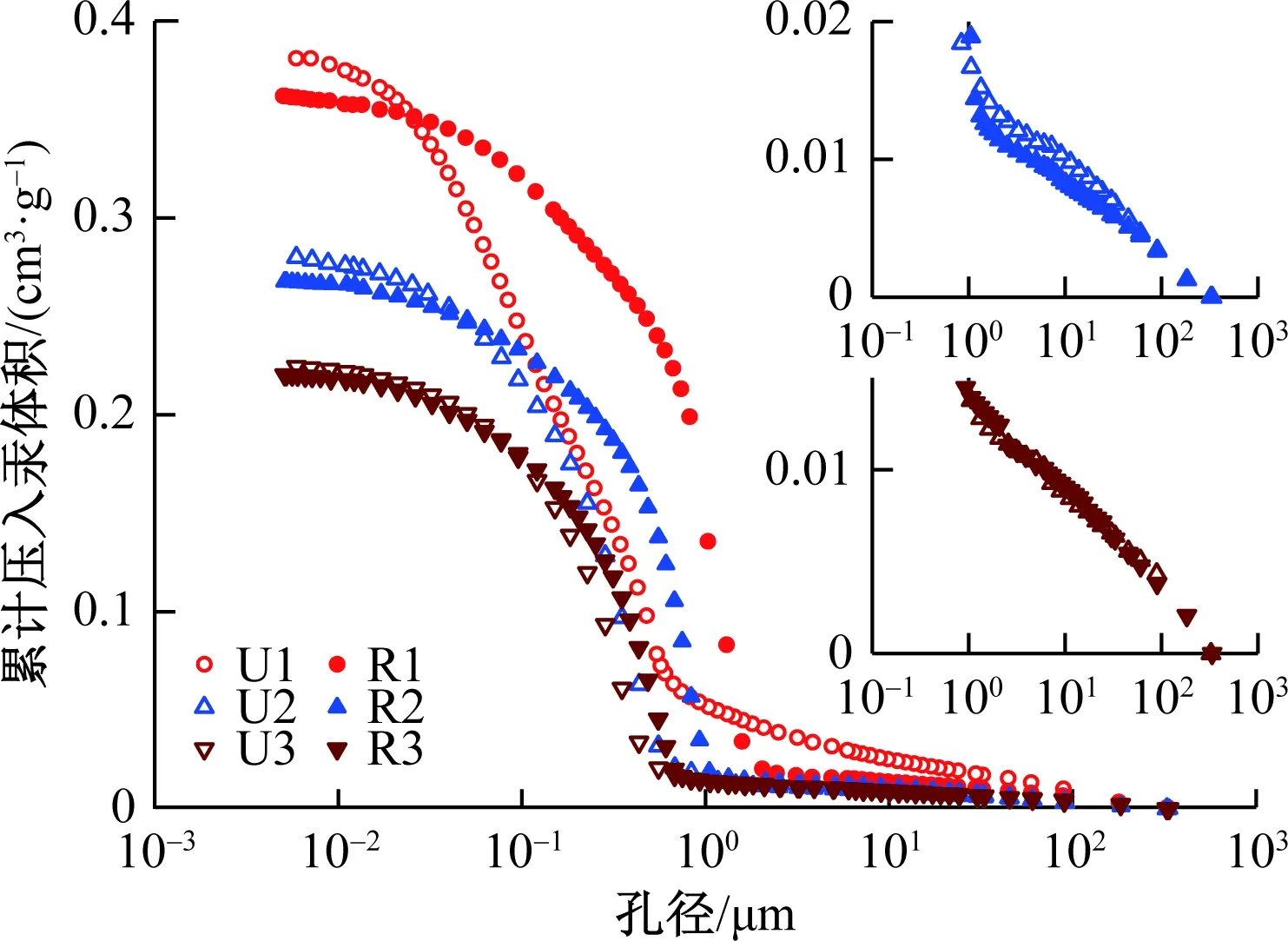
图6 孔隙比相近的原状样和重塑样的累积压入汞曲线Fig.6 Curres of a close cumulative intrusion volume of mercury of the undisturbed and reconstituted samples at the same void ratio

图5和图6为不同固结压力下，孔隙比ec相近的原状样和重塑样的孔径密度分布曲线和累积压入汞体积曲线。从图5可知，软黏土原状样和重塑样完全饱和时，孔径分布均为典型的单峰孔径结构，但两者的孔径分布曲线存在明显差异。与原状样的孔径分布密度曲线相比，重塑样的孔径分布范围明显更窄，峰值明显更高，说明泥浆样的孔径集中度更加明显，孔径分布也更加均匀。图6中的累积压入汞体积曲线也显示，当累积汞压入体积量急剧增加时，泥浆样的斜率明显大于重塑样的斜率，再次印证了泥浆样的孔径均匀性明显大于原状样。

从图5中还可以看出，重塑样的孔径分布密度曲线的峰值位置均位于原状样的右侧，说明重塑样的集中分布孔径大于相应原状样的集中分布孔径。随着孔隙比的减小，重塑样和原状样孔径之间的差距虽然逐渐缩小，但重塑样的孔径分布峰值始终在原状样的右侧。考虑到软黏土的孔径大小及其分布对其渗透性影响较大，且土体的孔径越大，其渗透系数也将越大，因此，相同孔隙比下重塑样的渗透系数应大于相应原状样的渗透系数。

然而，包括本文在内的众多试验结果却表明，相同孔隙比条件下，原状样的渗透系数都大于相应重塑样的渗透系数[9,11～12]，这主要是由于土体的渗透系数不是由集中分布孔径尺寸控制，而是由大孔径体积含量来控制的。按照张先伟等[18]确定的大孔径尺寸的划分及采用的分形曲线拐点划分孔径界限的方法确定的大孔径尺寸，分别以d>10 μm、d>3 μm和d>1 μm为界限对原状样和重塑样的相应孔径含量进行计算，得到表2所示的试验结果。从表2中可知，虽然在相同孔隙比条件下，原状样中d>1 μm孔径的累计含量明显小于相应的重塑样的累计含量。然而，对于d>10 μm和d>3 μm两种孔径尺寸的累计含量，原状样则明显大于相应的重塑样，且随着孔隙比的减小，两者的差距也逐渐减小。考虑到土的渗透系数主要是由大孔径的体积含量来控制的，且原状样的大孔径体积含量明显大于相应重塑样的大孔径含量，因此，可很好地解释为什么在同一孔隙比条件下，原状样的渗透系数将大于相应重塑样的渗透系数。

4 组构对渗透指数的影响

渗透系数的测定不仅需要耗费大量时间且测定结果往往离散性较大，难以准确确定。因此，不少国内外学者在根据试验方法测得渗透系数的基础上分析土体的孔隙比、含水率、塑性指数及密度等物理特性指标对渗透系数的影响，并建立了各种经验关系[4～6]。目前，描述软黏土渗透系数随孔隙比变化的最常用模型仍然是Taylor[19]建立的反映黏土渗透性的e-lgkv经验公式：

e-e0=Ck(lgkv-lgkv0)

(3)

式中：e0——土样初始状态的孔隙比；

kv0——初始状态e0下的渗透系数；

Ck——渗透指数。

Tevanas等[4]基于14种不同软黏土的试验结果，认为渗透指数可采用Ck=0.5e0的经验公式简单表示。然而，图7所示的国内外大量的渗透试验结果显示，渗透指数Ck与初始孔隙比e0比值的范围为0.314～0.489，平均值为0.408，其比值不仅明显小于Tevanas[4]等建议的经验关系值，而且不同土样的试验结果离散性很大，差值可达55%，与刘维正等[13]的统计结构基本一致。

图7 不同软黏土的ck-e0关系曲线Fig.7 ck-e0 curves of different soft clays

图7还显示，除了由于本试验用的重塑样前期受到较大的固结压力(70 kPa)，土体的初始孔隙比e0偏小导致原状样和重塑样的ck-e0关系基本一致外，其他四种软黏土在相同孔隙比时，原状样的渗透指数均大于相应重塑样的渗透指数，说明渗透指数ck与初始孔隙比e0的比值与软黏土的结构性密切相关，需要考虑结构性，尤其是土体组构对渗透指数的影响。

刘维正等[13]基于大量试验结果得到了渗透指数与初始孔隙比的关系， 但离散性大，将土体的液限孔隙比eL作为参数之一引入到渗透指数的经验公式构建中，使修正后经验公式的计算结果与实测结果更加吻合。然而，无论是初始孔隙比e0还是液限孔隙比eL，它们均无法反应软黏土沉积过程中形成的结构性对土体渗透特性的影响。由于软黏土结构中的胶结结构对土体的渗透系数基本没有影响[6,9,13]，只需考虑土体孔径大小及分布，即，组构对软黏土渗透特性的影响。因此，为更好反映软黏土结构性对渗透系数的影响，需在渗透指数计算中引入能反映土体孔径大小及分布的参数，即，土体组构参数。

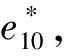
图8 不同类型压缩曲线的确定方法Fig.8 Determination of from compression curves of different types

图9 不同软黏土的关系曲线 curves of different soft clays

5 结论

(1)无论是原状样还是重塑样，土样的渗透系数均随着固结压力的增大而逐渐减小。但结构性的存在使原状样的渗透系数在结构屈服应力前后会发生明显的突变，且同一固结压力下原状样的渗透系数明显地大于相应重塑样的渗透系数。

(2)原状样和重塑样的渗透系数与孔隙比的变化模式大致相同，均为渗透系数随着孔隙比的减小而减小；但在相同孔隙比时，原状样中的结构性将使其渗透系数大于相应重塑样的渗透系数，这主要是由于不同土样的孔径大小及其分布差异对渗透系数的影响造成的，而且比较原状样和重塑样的大孔径含量可得到合理的解释。