磨损情况下水润滑橡胶轴承润滑特性分析

刘刚，李明

(西安科技大学 力学系，西安 710054)

水润滑橡胶轴承由于噪声小、无污染等优点，广泛应用于舰艇、船舶等推进轴系中[1]。随着舰船吨位的大型化，对水润滑橡胶轴承的润滑性能也提出了更高要求。水润滑橡胶轴承与油润滑的金属轴承相比，水的动力黏度系数约为润滑油的1/40～1/30[2-3]，橡胶的弹性变形比金属材料大几个量级。文献[4]讨论了弹性变形对轴承润滑特性的影响;文献[5]采用CFD方法分析了水润滑橡胶轴承的水膜压力分布;文献[6]通过测量水润滑橡胶轴承周向压力分布，将试验数据和CFD模拟结果进行了比较。

轴系启停过程中水润滑橡胶轴承尚未形成充分的润滑膜，轴承处于干摩擦或者混合润滑状态，此时容易使轴承下方发生磨损。文献[7-8]采用摩擦磨损试验机分别研究了载荷、速度、运行时间、含沙量等对复合橡胶轴承的摩擦因数和磨损率的影响；文献[9]分别在干摩擦、湿润滑以及完全水润滑条件下，在数显式高速环块摩擦磨损试验机上进行了摩擦磨损试验研究；文献[10-12]通过试验台对轴承的摩擦特性进行了相关研究。

现有研究工作主要关注水润滑橡胶轴承的摩擦因数和磨损率，对于磨损后轴承的润滑特性鲜有报道。实际上，磨损后的轴承内径形状发生改变，在未及时更换轴承的情况下，磨损轴承的润滑特性与磨损前有较大区别，进而影响到整个轴系的工作。鉴于此，现研究磨损后轴承的润滑特性，并与未磨损情况进行对比。

1 轴承概况

轴承磨损示意图如图1所示。轴承下方区域发生磨损(图1a)，假设磨损区域为与轴径相同的圆弧形。图1a中：ew为磨损区域的最大磨损厚度；Ob为轴承中心；Oj为轴心；Ω为轴颈角速度。轴系运行时，水润滑橡胶轴承轴颈位置及坐标系如图1b所示，此时由于水膜压力形成，轴颈上浮，具有偏位角。图1b中：φ为轴承轴向角度；e为偏心距；θ为偏位角；η轴沿轴承中心与轴心连线方向；ξ轴与η轴垂直。

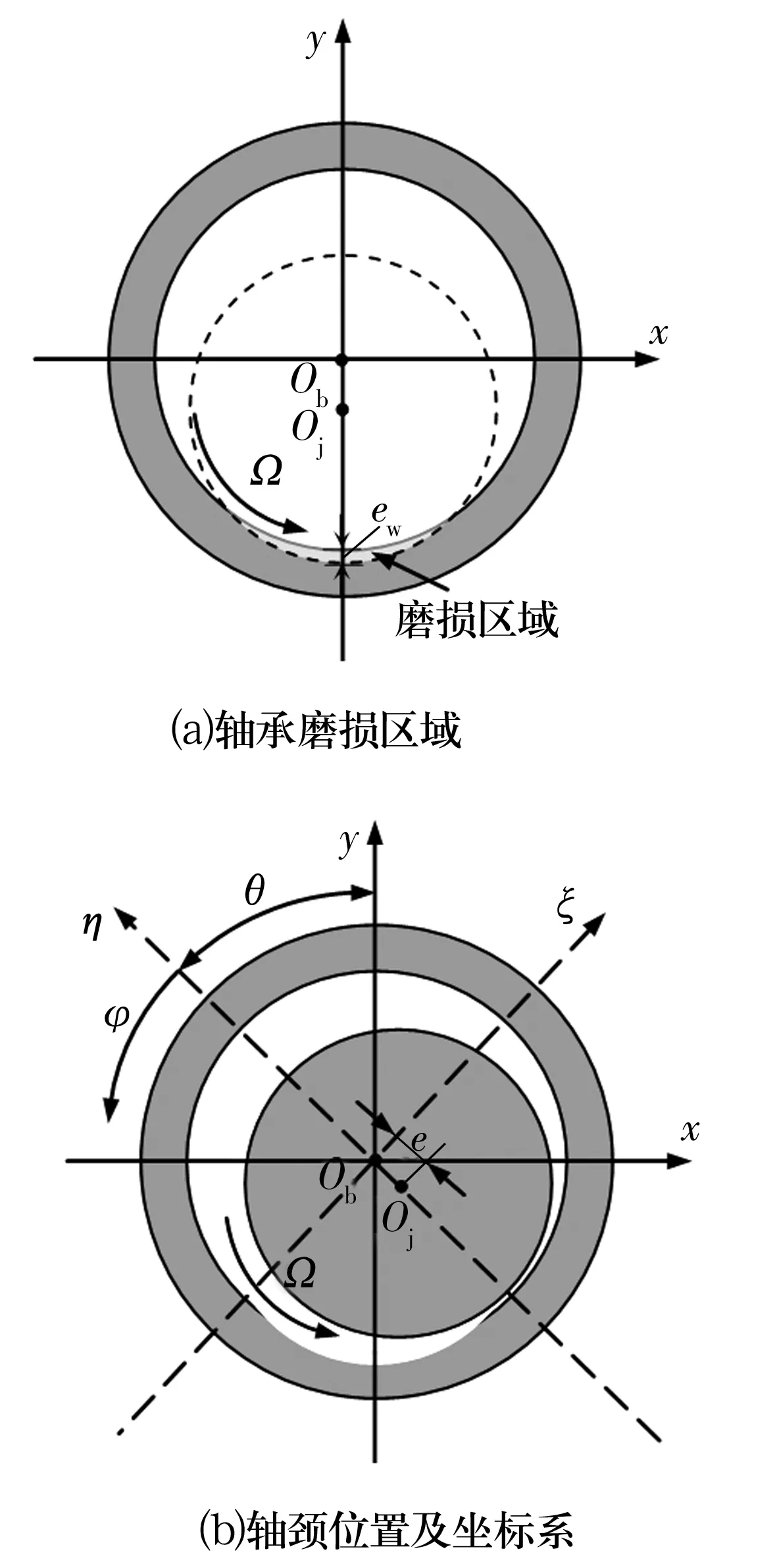
图1 轴承磨损示意图Fig.1 Diagram of worn bearing

以某船艉轴承为例进行计算，轴承参数见表1。

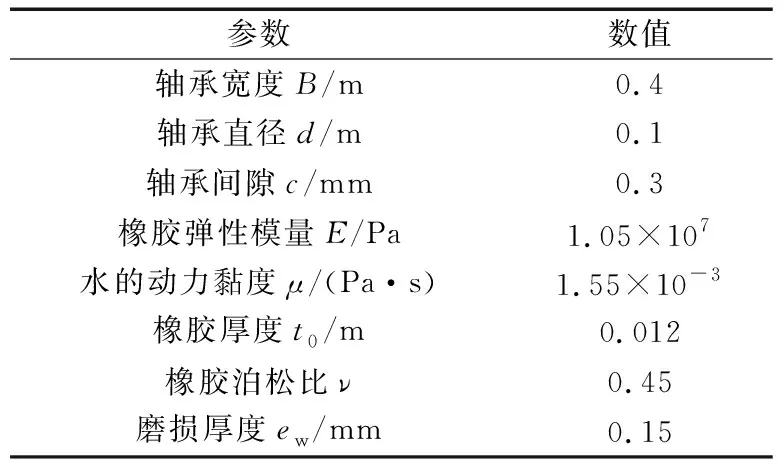
表1 轴承参数Tab.1 Bearing parameters

2 基本方程

2.1 Reynolds方程

忽略水的黏度和密度随压力变化，用于有限宽径向滑动轴承稳态条件下的Reynolds方程为

(1)

式中：h为水膜厚度；p为水膜压力；U为轴颈表面切向速度分量；x和z分别为沿轴承旋转方向和轴向的坐标。令

(2)

式中：r为轴承半径。将(2)式代入(1)式得到Reynolds方程的量纲一形式为

(3)

2.2 水膜厚度

考虑橡胶的弹性变形下分析水润滑橡胶轴承的弹流润滑特性。引入Winkler假设计算轴承橡胶衬层的弹性变形，即在连续分布载荷作用下，各点位移与受到的载荷成正比，橡胶衬层的弹性变形为

(4)

则水膜厚度方程为

h=c(1+εcosφ)+Δhe+Δhw，

(5)

式中：Δhw为磨损区域的水膜厚度增量。

量纲一的水膜厚度方程为

(6)

2.3 边界条件

采用Reynolds边界条件[13]，完整水膜的起始位置在最大水膜厚度处，破裂位置在经过最小水膜厚度之后的某一角度φ2处，满足水膜压力和压力梯度均为零，即

φ=0,P=Pa，

0<φ<φ2,P=P(φ)，

(7)

式中：Pa为环境压强，一般取为0。

2.4 承载力及偏位角

量纲一的承载力为

(8)

式中：Fξ和Fη分别为ξ轴和η轴方向的量纲一的承载力。

偏位角为

(9)

3 数值方法

采用有限差分法求解Reynolds方程。将轴承内表面展开为一个平面并划分网格(图2)，并对所有节点编号。在轴承圆周方向均匀划分m等份，节点用i编号，i=1～(m+1)；沿轴承长度方向均匀划分n等份，节点用j编号，j=1～(n+1)。每个节点的位置用(i,j)表示。节点(i,j)力上的压力值以Pi,j表示。根据差分原理，任意节点(i,j)的一阶和二阶偏导数均可由其周围的节点变量值表示，即可得到(3)式的差分形式。最终可将任意节点的压力用其周围的4个节点压力值表示，采用逐点超松弛迭代法求解。在满足精度要求且考虑计算时间的情况下，经过比较计算确定轴向网格数为60个，周向网格数为100。考虑橡胶衬层弹性变形的求解过程为：首先，由初始压力分布(一般设置为环境压强)计算橡胶弹性变形和水膜厚度，将其代入方程Reynolds方程得到各节点水膜压力；然后，重新计算橡胶弹性变形和水膜厚度，再代入方程Reynolds方程求解水膜压力，如此迭代直到得到收敛解[14]。

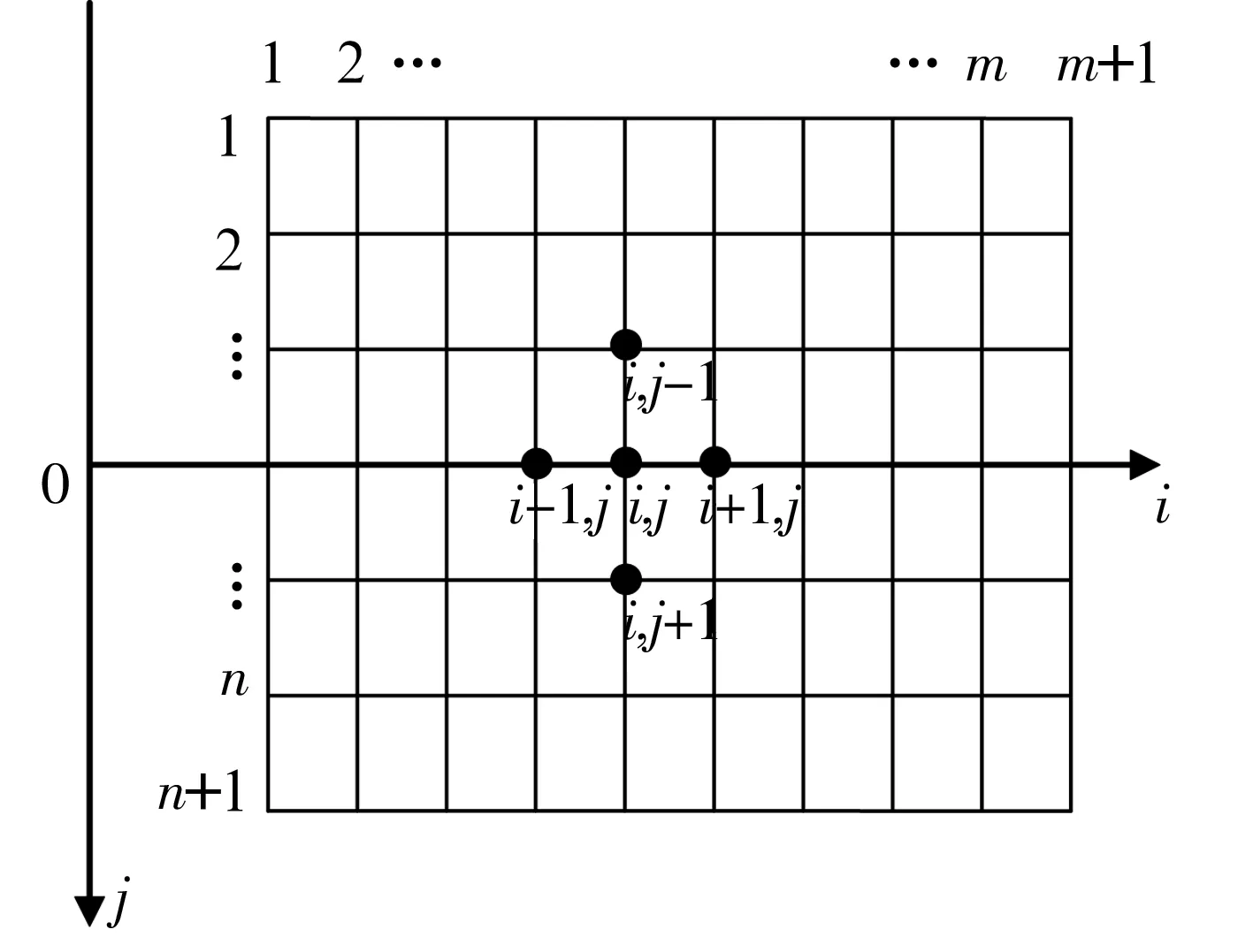
图2 网格划分Fig.2 Meshing

4 结果与分析

4.1 水膜厚度

偏心率为0.9时，2种情况下水膜厚度的分布情况如图3所示。对比图3a、图3b可以看出，在未磨损情况下，水膜厚度均匀变化；在磨损情况下，水膜厚度在最小间隙附近发生转折，形状与未磨损时呈反对称，这是由于磨损区域存在，使得在该区域水膜厚度增加。假设磨损的形状较为规则(磨损的区域形状为与轴径相同的圆弧形)，因此在磨损起始、结束位置有一定转折。由图3c可以看出，水膜厚度增加的区域范围约为115°～205°(随偏心率、磨损量变化)，不是关于最小间隙对称分布，而是在最小间隙偏前的位置。这是因为在轴系运转时，轴颈有一定的偏位角，使最小间隙位置偏离磨损区域(图1b)。

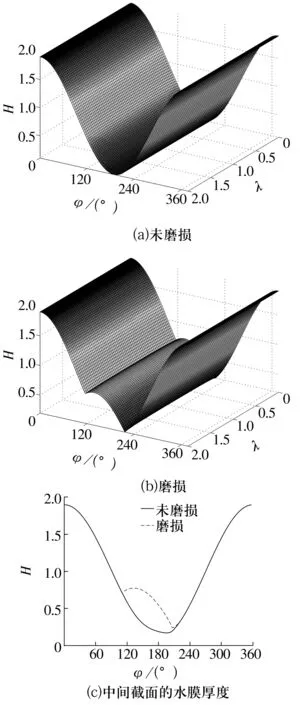
图3 相同偏心率下的水膜厚度Fig.3 Water film thickness under same eccentricity

4.2 水膜压力分布

偏心率为0.9时，2种情况下的水膜压力分布如图4所示。对比图4a、图4b可以看出，磨损使最大水膜压力大幅降低，水膜形状趋于平缓。这是因为在原来最小水膜厚度的位置水膜厚度增加，动压效应减弱，引起压力降低，水膜厚度变化引起水膜压力分布形状变化。同时水膜的最大压力位置和水膜破裂位置均延后，这是因为最小水膜厚度位置延后。

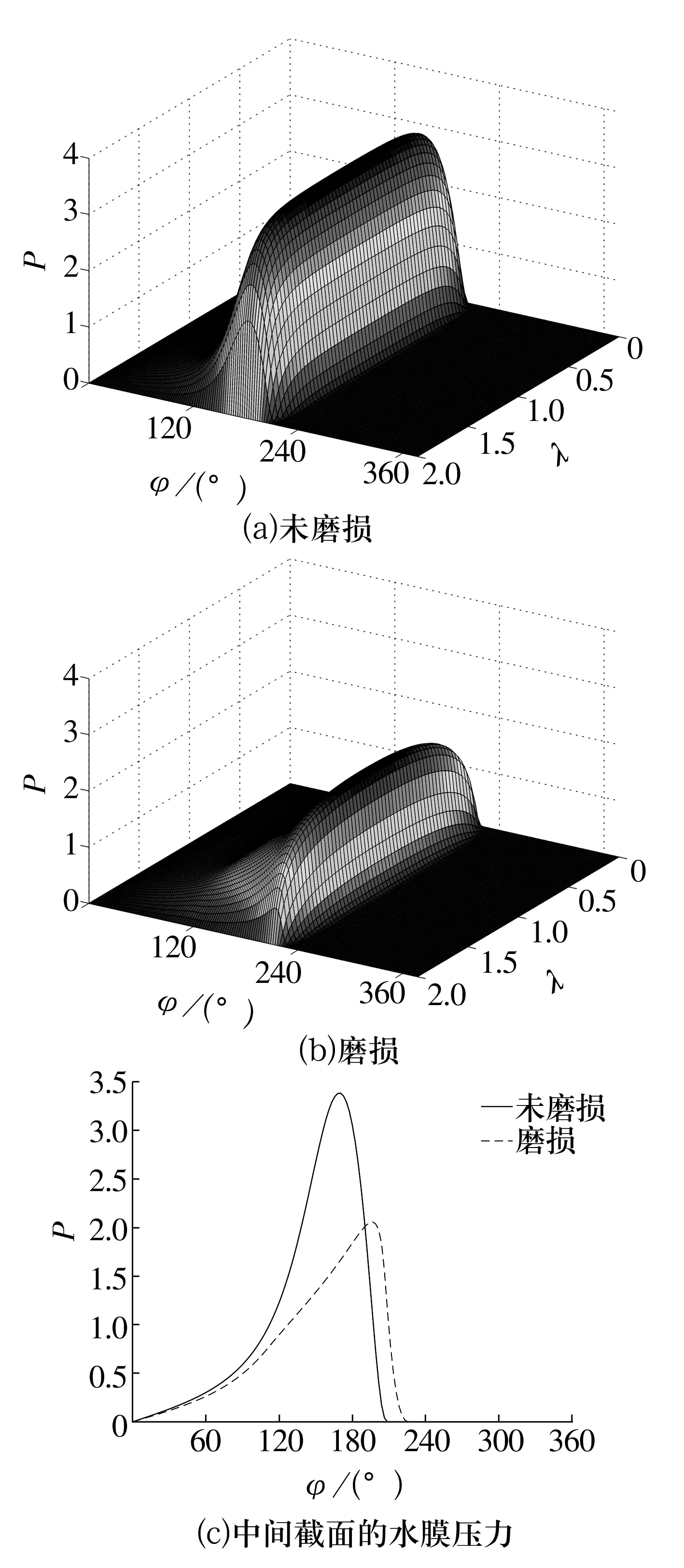
图4 相同偏心率下的水膜压力Fig.4 Water film pressure under same eccentricity

4.3 承载力

量纲一的承载力随偏心率的变化曲线如图5所示。由图可以看出，随着偏心率的增加，承载力增加，磨损情况下的承载力小于未磨损下的承载力；当偏心率较大时，二者差距更加明显。这是因为磨损后的轴承在底部轴承间隙增加，由于楔形效应产生的动压减弱，引起承载力下降，且偏心率越大，楔形角的变化率越大，承载力下降越快。

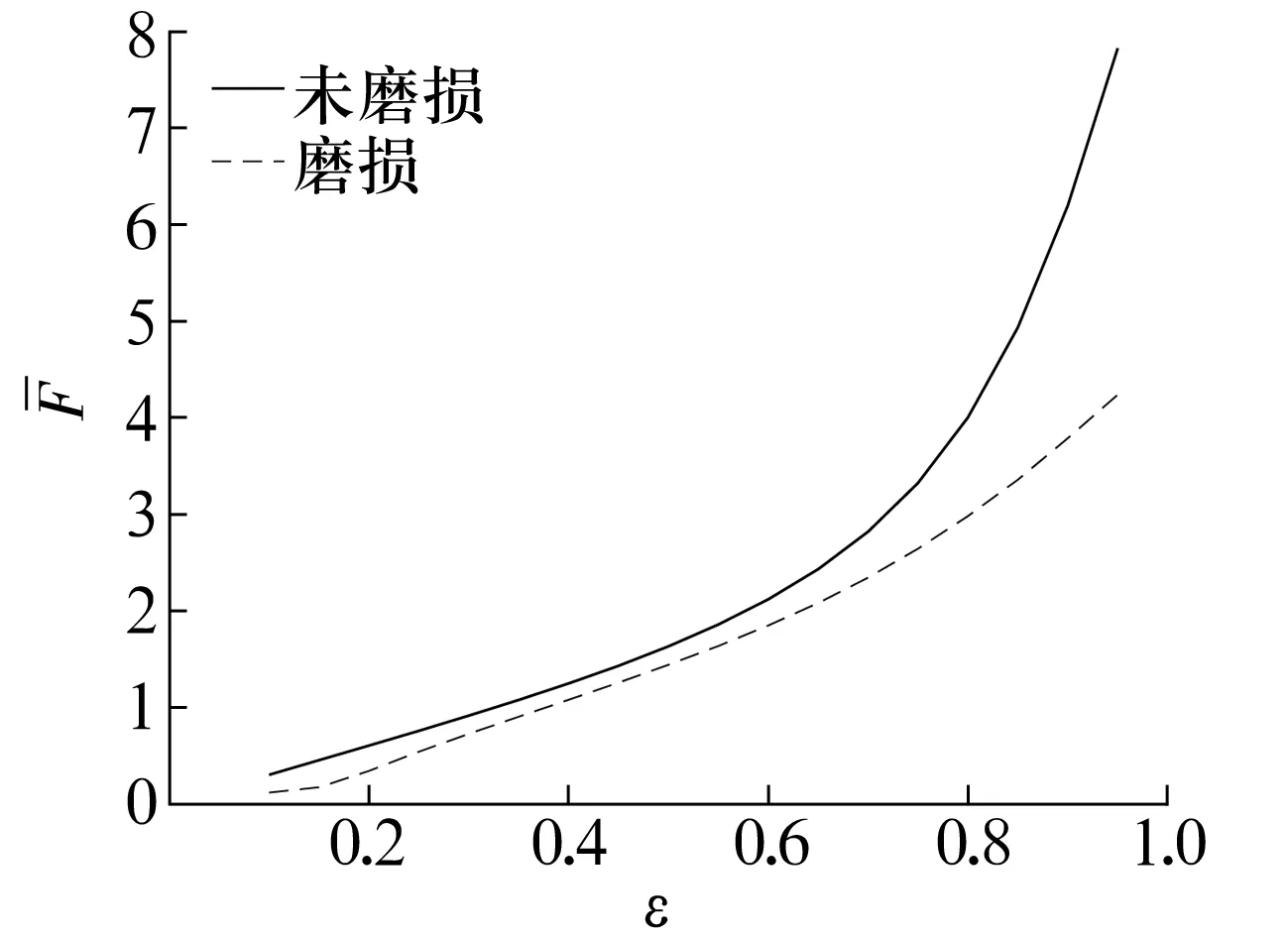
图5 量纲一的承载力随偏心率的变化曲线Fig.5 Variation curve of dimensionless load capacity with eccentricity

4.4 偏位角

偏位角随偏心率的变化曲线如图6所示。由图可以看出，未磨损情况下，轴颈的偏位角随偏心率的增加而减小，这是由于转速相同时，载荷越大，偏心率越大，引起轴颈下沉，偏位角减小。磨损情况下，轴颈的偏位角随偏心率的增加先增大后减小，这是由于偏心率较小时，磨损区域使得水膜间隙的楔形效应减弱，轴颈下沉；当偏心率增加到0.4～0.5时，楔形效应增强，轴颈上浮；当偏心率继续增加时，轴颈由于载荷增加再次下沉。

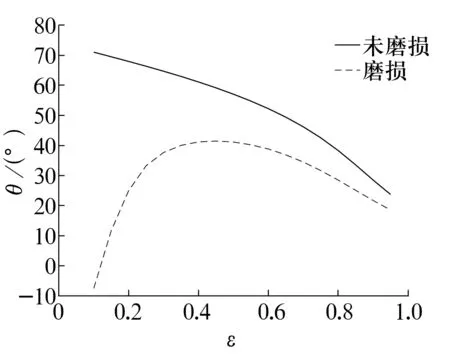
图6 偏位角随偏心率的变化曲线Fig.6 Variation curve of attitude angle with eccentricity

2种情况下的载荷平衡圆如图7所示，其中，径向坐标表示偏心率，周向坐标表示偏位角。图7直观地显示了不同偏心率下轴颈所在位置。由图可以看出，未磨损情况下，随着偏心率的增加，轴颈逐渐下沉至轴承底部；磨损情况下，轴颈下沉路径发生变化，偏心率较小时呈现不规则形状，影响轴承的工作特性以及轴系的运行。

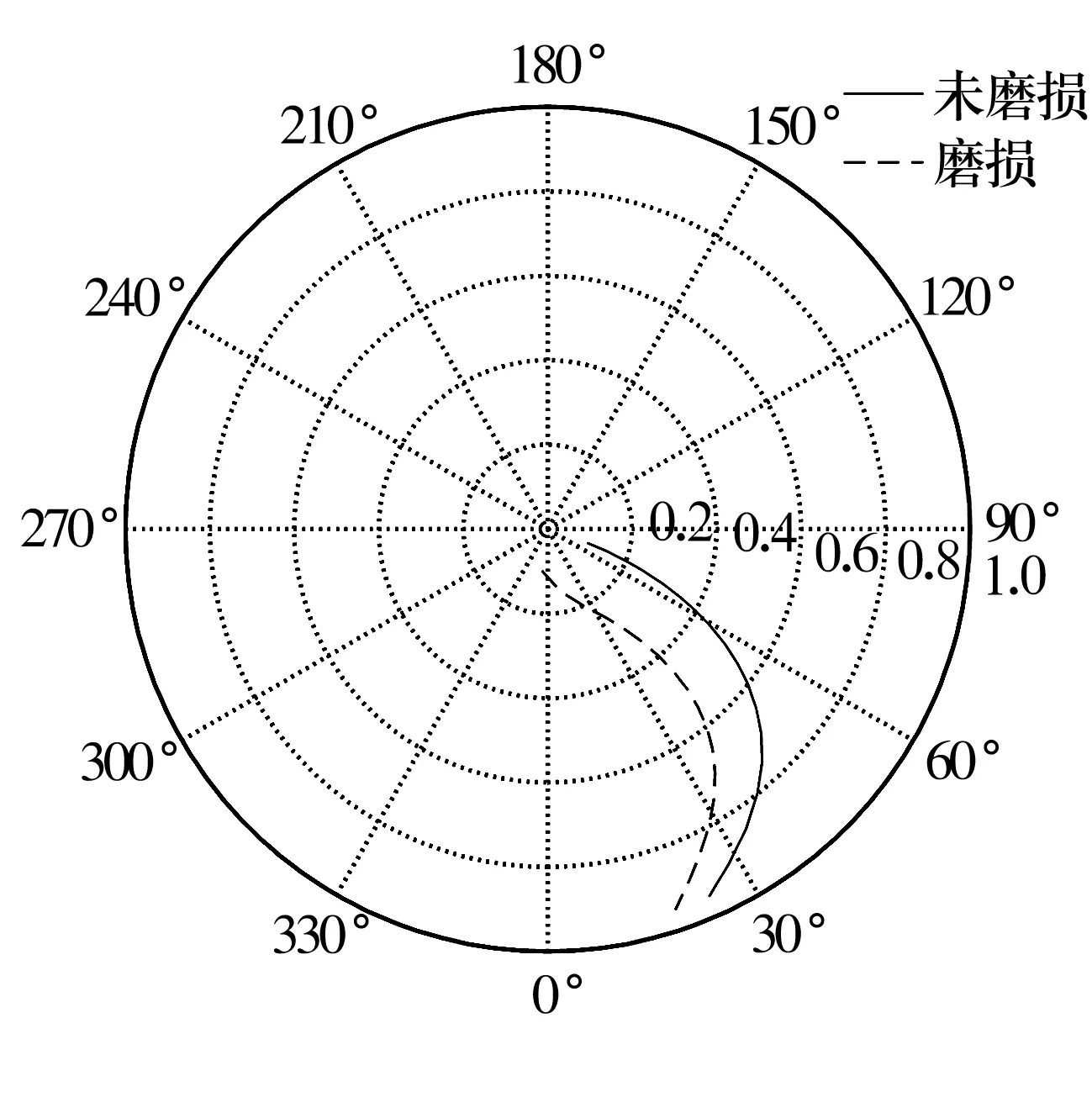
图7 载荷平衡圆Fig.7 Circle of load balancing

5 结论

1) 磨损时水膜厚度在磨损区域发生转折，形状与未磨损时呈反对称，水膜厚度增加，该区域位于最小间隙偏前的位置。

2) 磨损使最大水膜压力大幅降低，水膜最大压力位置和水膜破裂位置均延后。磨损情况下的承载力小于未磨损下的承载力。

3) 未磨损情况下，轴颈的偏位角随偏心率的增加而减小；磨损情况下，轴颈的偏位角随偏心率的增加先增大后减小。

4) 未磨损情况下，轴颈随着偏心率的增加下沉至轴承底部；磨损情况下，轴颈运动路径发生变化，改变了轴承的工作特性，影响轴系的运行。