八沟槽水润滑橡胶轴承多参数流固耦合分析

王楠，王明武，杨帆，梁应选

(1.陕西理工大学 机械工程学院，陕西 汉中 723001；2.陕西省工业自动化重点实验室，陕西 汉中 723001)

水润滑橡胶轴承具有环保、耐磨、低耗等优点，可有效避免油润滑轴承的密封失效、温度过高以及过度摩擦磨损等问题，广泛用于船舶、水/汽轮机、水泵等水力机械。水润滑橡胶轴承的轴瓦摩擦表面有凹面、平面和凸面3种形式，一般采用沟槽设计，沟槽横截面多采用U形结构(也有V形、T形、矩形等结构)，沟槽方向多为纵向(也有周向螺旋沟槽)。因纵向U形沟槽橡胶轴承排污、散热及润滑效果较好，加工方便，应用较多。由于轴承承载区有沟槽，橡胶弹性模量小且不可压缩，橡胶轴瓦易发生变形，加之水的黏度低，因此会导致轴承水膜压力较小，不易形成完整连续的水膜。为了保证一定的承载能力，通常要减小轴承间隙，这就对轴承设计提出了较高要求；同时，启停与低速重载工况下轴承润滑状态复杂多变(干摩擦-边界润滑-混合润滑-全膜润滑)，因此，亟需对该类轴承特性及润滑机理进行深入研究。

目前，水润滑橡胶轴承的研究方向主要可分为：结构设计与材料选择；润滑特性。相关学者与研究机构在轴承结构设计与材料选择方面虽然进行了大量研究[1-7]，但至今仍然没有一套合理的水润滑橡胶轴承设计标准规范，在轴承轴瓦摩擦表面类型以及沟槽类型、方向、数量与分布选择上还存在不同观点[8]。对于橡胶轴承特别是带沟槽的橡胶轴承润滑特性的研究，运用流体润滑理论以及试验分析后初步认为轴承内部不存在完整连续润滑膜，轴承处于混合润滑状态[6, 8, 9-17]，轴承在水润滑过程中是否会产生弹性流体动压润滑仍有待理论与试验证明。橡胶轴承的研究方法分为软件建模仿真[3-15]与试验研究[1-2, 10, 13, 15-18]，由于滑动轴承的密闭性、内部结构的多样性(轴瓦材料、板条与沟槽类型及分布等)，实际运行工况及轴承润滑剂流动的复杂性，构造试验台并进行试验研究较为困难，因此多采用软件对研究对象进行建模与仿真分析。

目前，水润滑橡胶轴承的研究工作还存在以下问题：多数文献的软件建模与数值计算中简化过多，且未从工程应用出发考虑问题；由于试验研究较为困难，在轴承润滑特性方面，多数文献主要是软件建模与数值计算等理论研究。

鉴于此，针对用于某潜水艇螺旋桨附近的2种结构的八沟槽橡胶轴承，基于实际工况条件，采用双向流固耦合方法，应用ANSYS软件建立轴承模型及其间隙模型，并进行仿真(考虑气穴现象)，分析轴承各性能参数、橡胶变形之间的耦合关系及其相互影响，与刚性轴承进行对比，结合轴承水膜压力试验对仿真结果进行验证。

1 研究对象与分析方法

水润滑橡胶轴承外圈为钢材，内圈轴瓦为橡胶；板条结构分别为凹面、平面2种(图1)，沟槽为轴向U形结构，沿周向均匀分布且边缘进行圆角处理；试验轴承进行了5∶1缩放，转轴直径Ds=100 mm，轴承内径d=100.8 mm，外径D=120.8 mm，橡胶衬层厚度h=6 mm，轴承平均半径间隙c=0.4 mm，2种轴承的长径比均为4.25∶1与2∶1，轴向供水。由于橡胶弹性模量较小，且具有不可压缩特性，因此轴承在轻载时其接触表面也会产生弹性变形，对轴承特性与润滑机理产生很大影响；同时，由于存在多沟槽，轴承结构复杂。因此，与刚性轴承相比，表征轴承特性的相关参数(水膜压力、水膜厚度、承载力等)的变化规律是不同的。

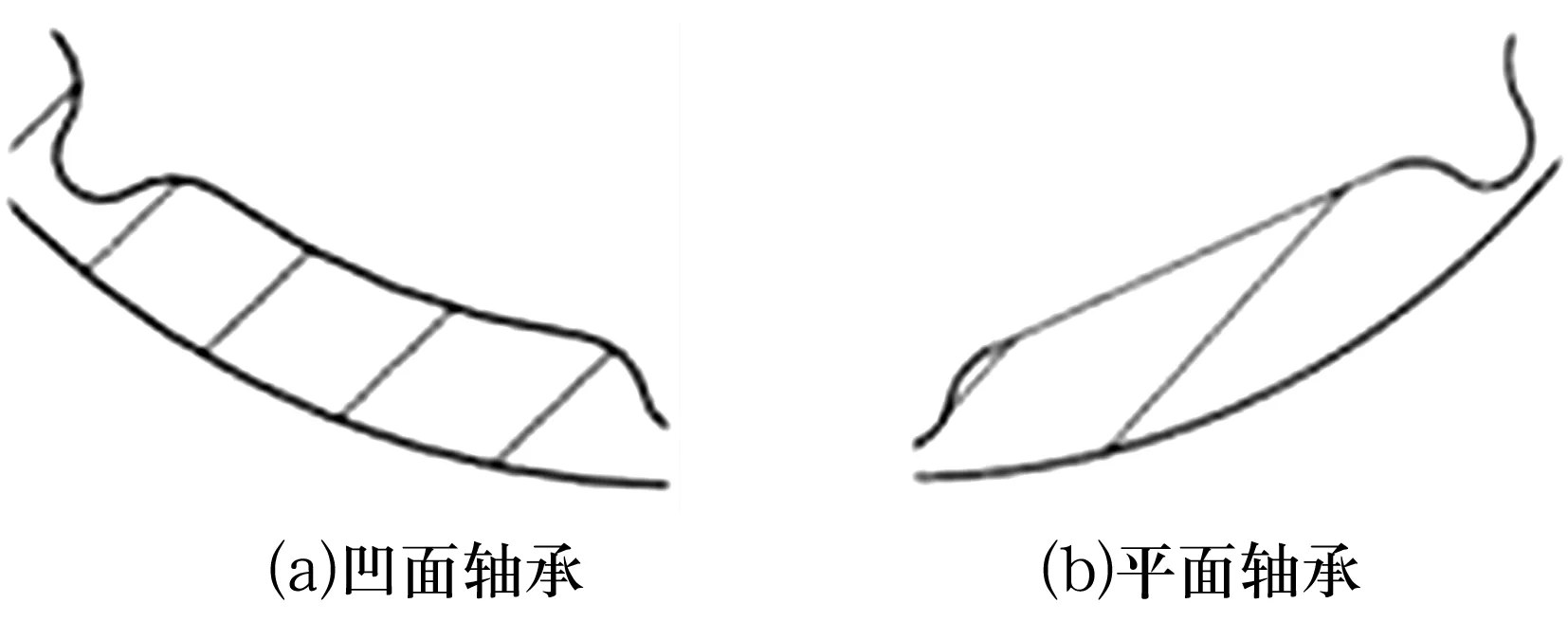
图1 橡胶轴承横截面结构示意图Fig.1 Cross section structure diagram of rubber bearing

由于研究重点是水流压力与橡胶变形之间的相互影响以及由于橡胶变形而引起的水膜压力变化，因此应用ANSYS双向流固耦合模块建立橡胶轴承及其间隙模型(固体域与流体域)，对橡胶变形引起的水膜压力、水膜厚度、承载力以及与轴转速、载荷、长径比等参数的变化关系及规律进行分析。由于试验轴承在轴向上的变形受到端盖的限制，外圈固定，且在受力时刚性轴套的变形远小于橡胶轴承的变形，因此轴向变形可忽略不计。双向流固耦合方法流程图如图2所示。方法如下：1)设置位移为0，轴承橡胶与轴套的交界面为固定面，轴承内表面为流固耦合面，设置时间步长，生成input文件。2)将划分好的水膜间隙网格导入CFX中，并对网格的位置与尺寸进行调整，设置流场分析类型为多相流耦合，导入input文件；在流域(domain)设置中，选取多相流模型中的气穴模型，定义流体材料属性，设置主轴旋转轴、转动速度及流固耦合面。3)单击Output control按钮，通过Select various选择输出变量，设置输出控制属性，并在迭代开始后对轴承各参数进行监测。

2 建模与求解

2.1 轴承及其间隙模型的建立

由于水在轴承中流动时的温度变化很小，故不考虑温度对轴承润滑性能的影响。参数设置如下：轴承结构参数按照前文设置，环境温度为25 ℃，水密度ρ1=998 kg/m3，黏度μ=8.90×10-7m2/s，橡胶密度ρ2=1 550 kg/m3，弹性模量E=7.75 MPa，泊松比ν=0.47。

橡胶轴承及其间隙模型分别如图3、图4所示。由于平面轴承结构与凹面轴承相似，因此只对凹面轴承建模过程进行说明。建模时，外圈为钢材，内圈为橡胶，由于钢材刚度远大于橡胶刚度，因此外圈变形可忽略，只考虑轴承内圈变形。为了提高计算速度及精度，轴承与其间隙模型的网格划分都采用六面体单元结构网格。六面体单元的长度为0.4 mm，采用sweep方法进行划分，轴承模型中径向方向为8层，轴向10等分，网格节点数为123 414，单元数为24 560；轴承间隙模型中径向为10层，轴向12等分，网格节点数为232 536，单元数为47 894，经检测，固体域与流体域网格质量均在0.92以上。

图3 轴承模型及网格划分Fig.3 Model and meshing of bearing

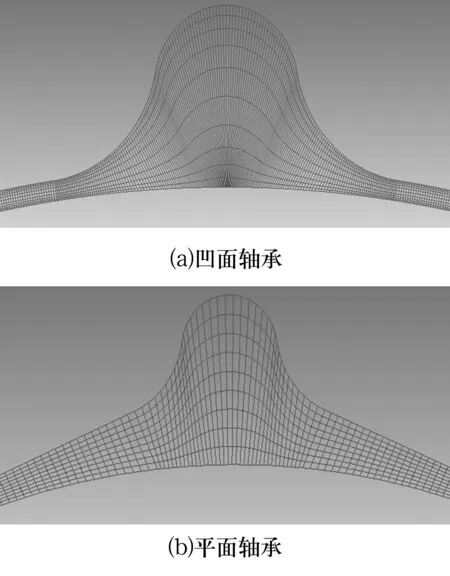
图4 轴承间隙模型及网格划分Fig.4 Model and meshing of bearing clearance

2.2 边界条件与求解模型的选取

采用考虑气穴的质量守恒边界条件(JFO边界条件)，其是针对Reynolds边界条件不能很好解释油膜再次形成时的情况而提出的，不仅满足油膜破裂处的质量守恒，在油膜再形成处还满足质量守恒，充分考虑了油膜分离和重新形成的情况。应用FLUENT工具直接求解N-S方程，由于滑动轴承发散楔形区内，恒定温度下，当润滑介质压力下降到饱和蒸气压以下时，即无法承受负压发生破裂形成气穴而产生空化现象，因此采用与JFO边界条件原理相同的气穴模型进行边界条件设定。

选择求解模型前，首先判断流体状态。轴颈半径R=50 mm，间隙比c/R=0.008，轴转速ω变化范围为50～200 rad/s，由Taylor判据可得，实际流体Reynolds数Re=1 198>1 000(临界值)，因此流体为湍流状态。橡胶轴承工作中，由于沟槽的存在，流体运动带有强烈旋转并紧贴弯曲壁面，因此湍流模型采用修正过的RNGκ-ε模型。气穴模型选择Schnerr and Sauer，饱和蒸气压Ps设为3 540 Pa，材料设置中增加water-vapor，密度为0.554 2 kg/m3，黏度为1.34×10-5Pa·S。选用压强速度耦合求解器(SIMPLEC算法)。考虑气穴时的水润滑轴承残差曲线如图5所示。经过反复验证，压力迭代松弛因子和动量方程的松弛因子为0.1，其他松弛因子为0.3时，收敛速度和精度较高，收敛标准为所有控制方程的迭代残差都小于1×10-3。

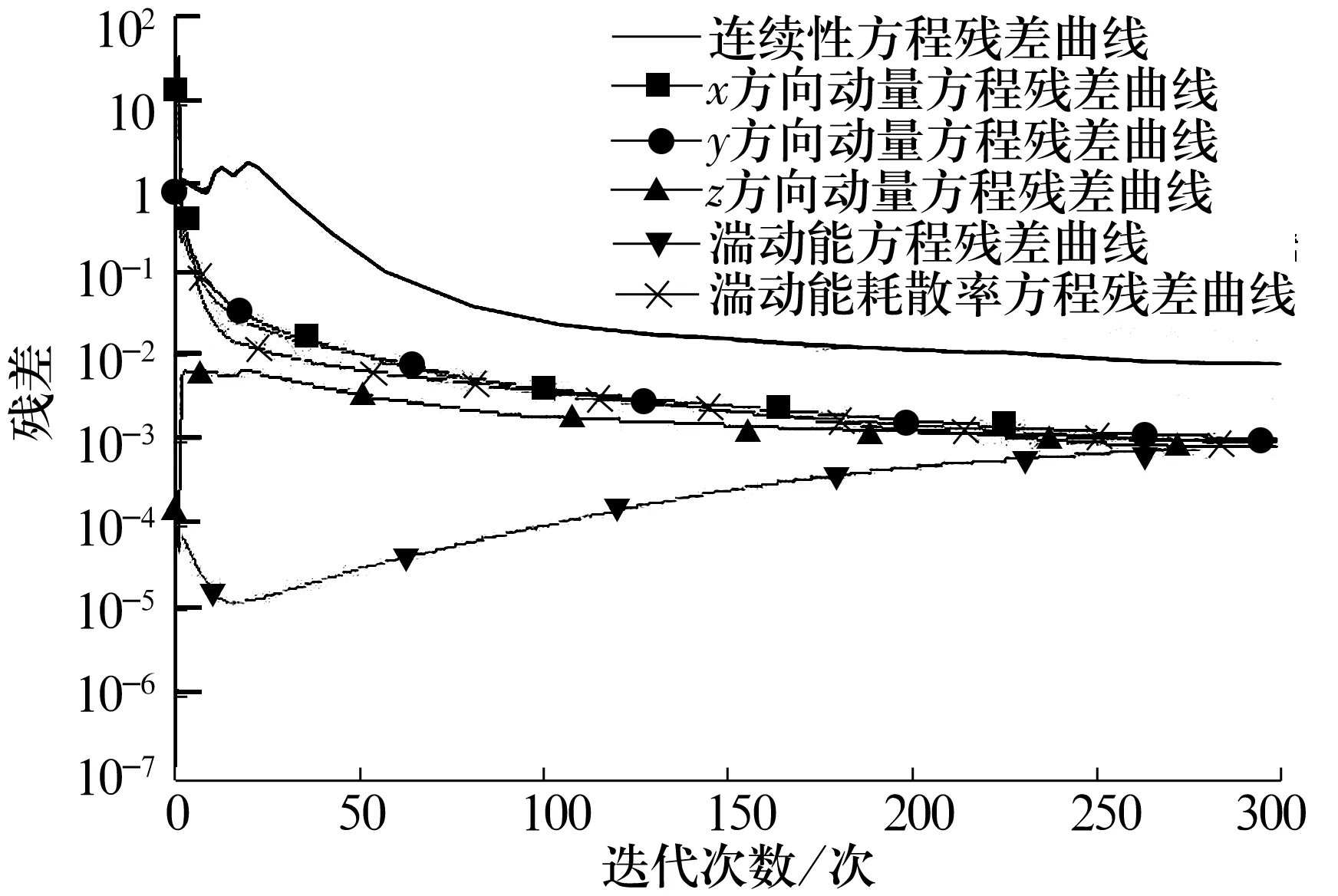
图5 考虑气穴时的轴承残差曲线Fig.5 Residual error curves of bearing while considering cavitation

3 仿真分析

3.1 不同参数对轴承性能的影响

在最大比压0.024 MPa、不同外部载荷Fw下，凹面轴承(长径比4.25∶1)偏心率ε、最大水膜压力Fm随轴转速ω的变化曲线如图6所示(平面轴承在上述参数下的变化规律与此类似)。由图6a可知，载荷不变时，随着轴转速增加，轴承偏心率减小(最小水膜厚度增加)；由图6b可知，最大水膜压力随轴转速的增加逐渐减小并趋于稳定，因此，轴承整体水膜压力分布也将逐渐趋于稳定，轴承总的承载能力不变。由此可推断，载荷不变时，当轴转速增大到临界转速时，轴承将不能形成动压润滑所需压力，此时若轴转速继续升高，轴承与轴将产生接触。

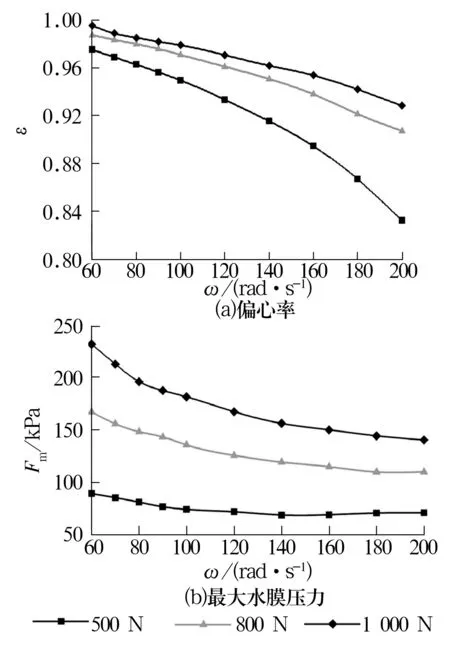
图6 偏心率、最大水膜压力随轴转速的变化曲线Fig.6 Variation curves of eccentricity and maximum water film pressure with shaft speed

外部载荷为500 N时，在不同长径比L/d下，轴承偏心率ε、偏位角θ随Sommerfeld数So的变化曲线如图7所示。由图可知，长径比为4.25时轴承的偏心率小于长径比为2时的偏心率，而偏位角θ情况则相反。因此，载荷不变时，长径比越大，轴承偏心率越小，水膜厚度越大，轴承越不易与轴产生接触。

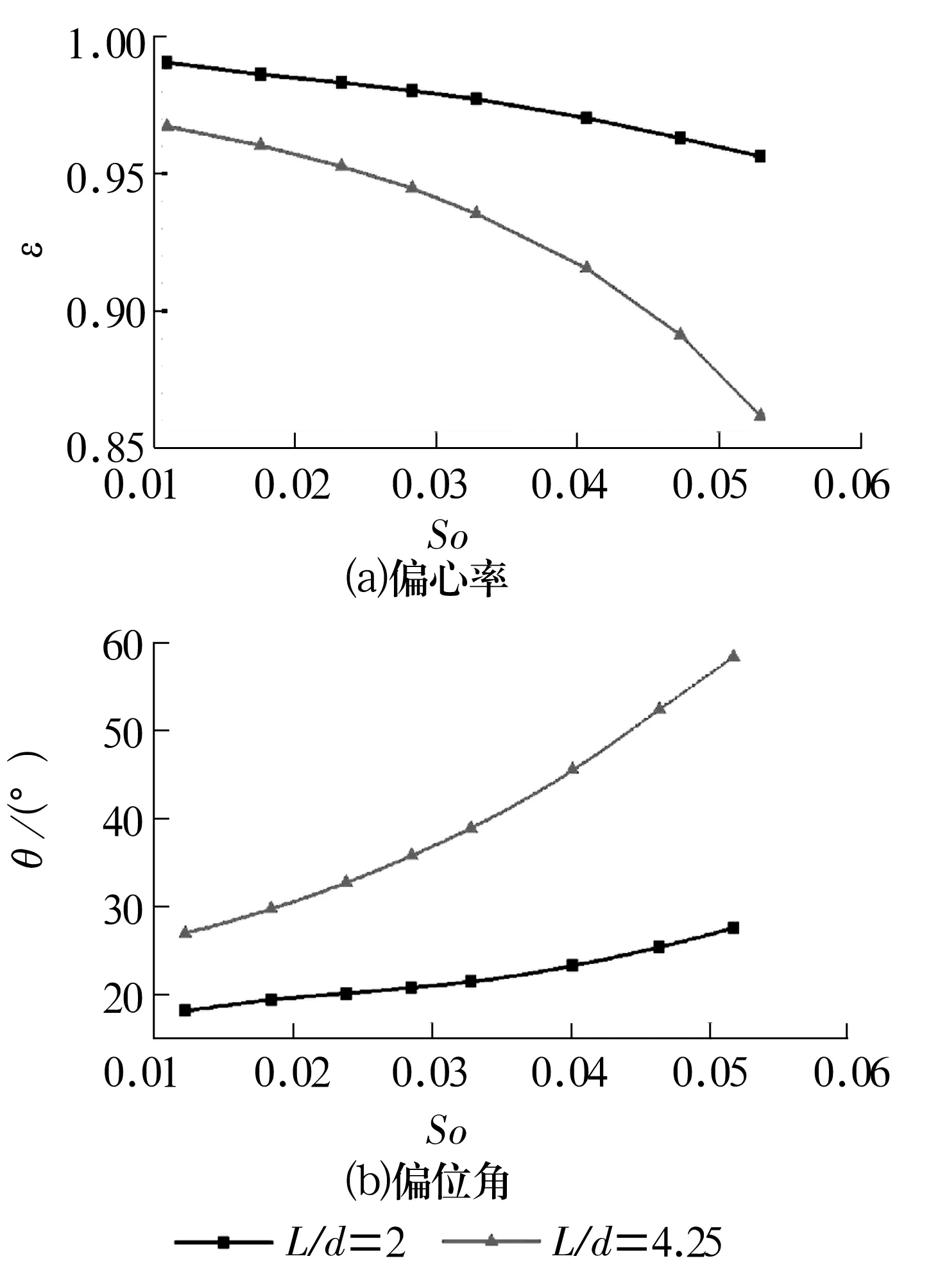
图7 偏心率、偏位角与Sommerfeld数变化关系Fig.7 Sommerfeld variation relationships among eccentricity,attitude angle and number

轴转速为100 rad/s、偏心率为0.8时2种轴承的水膜压力Ff分布云图如图8所示。轴向Z=0.2 m截面处不同偏心率下2种轴承的周向连续水膜压力分布曲线(以正上方沟槽中心为零点)如图9所示。由图8a可知，轴承板条上的压力明显大于沟槽处的压力，且其压力分布变化较平缓；由图8b可知，板条上的压力分布变化较大，其中间压力远高于两端压力，说明在板条上形成了较为明显的压力峰，该现象在图9b中表现更为明显。此外，在承载区(周向角在120°～180°,-120°～-180°之内)内，凹面轴承基本无空化现象，而平面轴承空化现象较严重，表明凹面轴承润滑效果优于平面轴承。

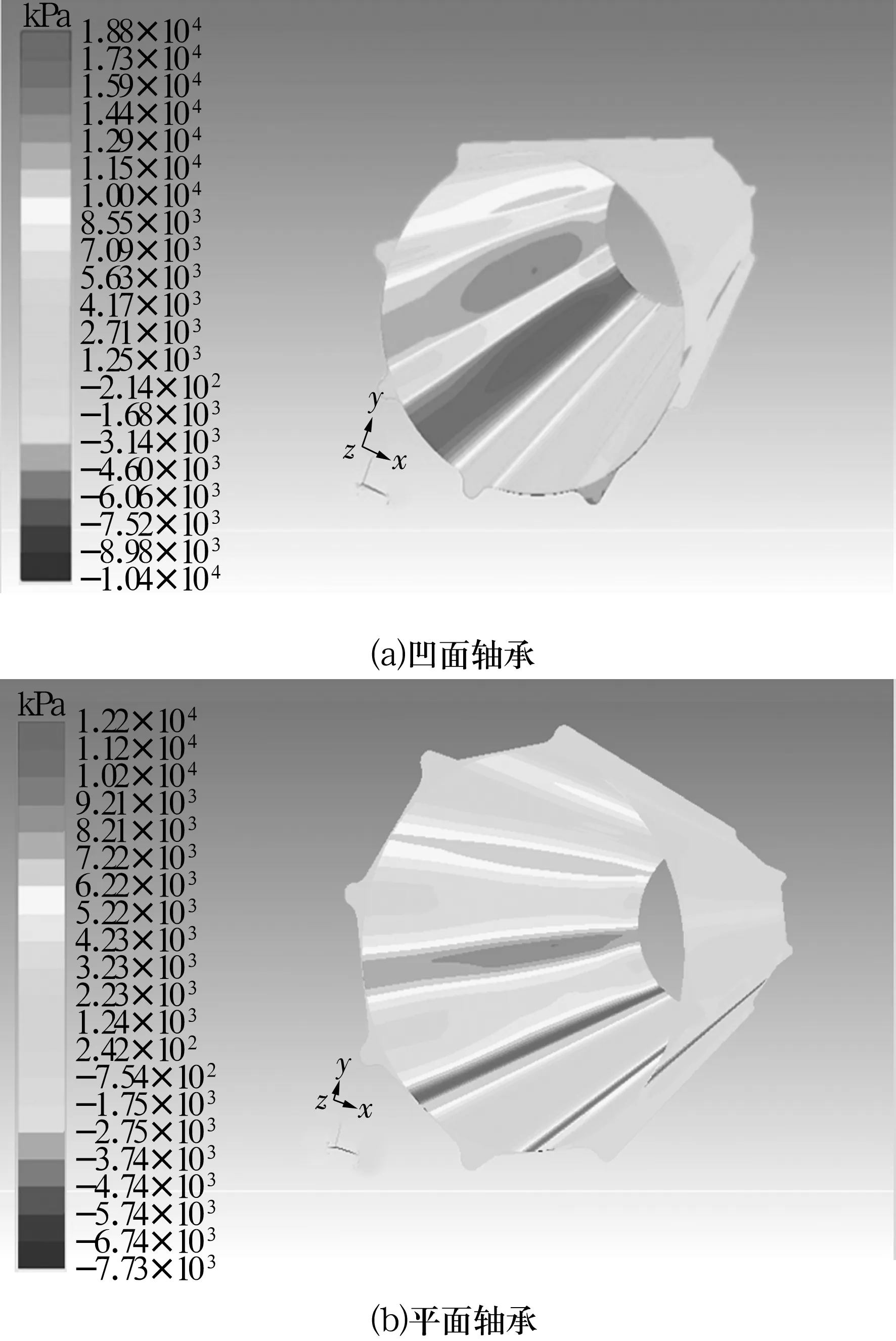
图8 橡胶轴承水膜压力分布云图Fig.8 Water film pressure distribution nephogram of rubber bearing

滑动轴承中，压力分布大小可作为衡量轴承承载力大小的重要指标。由图9可知，偏心率为0.2时，轴承水膜压力的最大值以及峰-峰值均较小，说明偏心率较小时，轴承动压效应小，此时压力变化不明显，对应轴承承载力也较小；随着偏心率由0.2增大到0.8，轴承动压效应逐渐增强，因此最大水膜压力及压力峰-峰值逐渐增大，轴承承载力大幅提高。平面轴承每个板条上压力峰较尖锐，凹面轴承压力变化平缓，同一偏心率下，凹面轴承最大水膜压力远大于平面轴承，由此表明，凹面轴承承载能力优于平面轴承。此外，每个偏心率下2种轴承都出现了负压，且平面轴承负压区多，表明水膜是部分连续的，平面轴承润滑状态较差。

通过FLUENT后处理过程可得到轴承在不同偏心率和轴转速下的承载力变化，如图10所示。由图可知，偏心率为0.2时，轴转速从50 rad/s增大到200 rad/s，凹面和平面轴承承载力增量分别为230.3，91.7 N；偏心率为0.8时，转速从50 rad/s增大到200 rad/s，凹面和平面轴承承载力增量分别为996.3,477.0 N，分别是偏心率为0.2时承载力的4.33倍和5.21倍。因此，随着轴转速增加，轴承动压效应增强，轴承承载力Fc逐渐增大。偏心率较小时，轴旋转所带来的动压效应并不明显；偏心率逐渐增大时，轴承动压效应逐渐增强，轴承承载力得到大幅提升。

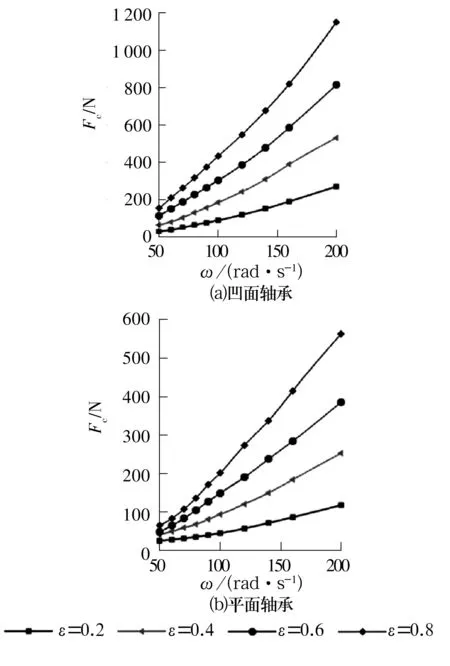
图10 承载力和偏心率、轴转速变化关系Fig.10 Variation relationships among load capacity,eccentricity and shaft speed

外部载荷为1 000 N、偏心率为0.8时，2种轴承的最小水膜厚度hm与承载力Fc随轴转速的变化曲线如图11所示。由图11a可知，相同载荷与转速下，凹面轴承最小水膜厚度大于平面轴承，即凹面轴承更易形成动压水膜润滑。由图11b可知，转速为50 rad/s时，平面、凹面轴承承载力分别为64.4，153.9 N，差值为89.5 N；当转速增加到200 rad/s时，平面、凹面轴承承载力分别为541.4，1 150.2 N，差值为608.8 N；随着转速增加，承载力差值逐渐增大。因此，凹面轴承承载力优于平面轴承，即相同负载下，平面轴承更易与轴发生接触。

图11 最小水膜厚度与承载力随轴转速的变化曲线Fig.11 Variation curves of minimum water film thickness and load capacity with shaft speed

3.2 橡胶变形对轴承特性的影响

轴转速200 rad/s，外部载荷500 N时，2种轴承的板条变形分布云图如图12所示。由图可知，凹面轴承的橡胶变形主要发生在水膜最小间隙轴承板条上，由于橡胶弹性模量较小且具有不可压缩性，板条两边压力相对中间压力较小(图12a)，因此，这种两边小、中间大、相互独立的压力会使板条两边变形隆起，中心凹陷，形成“水囊”。

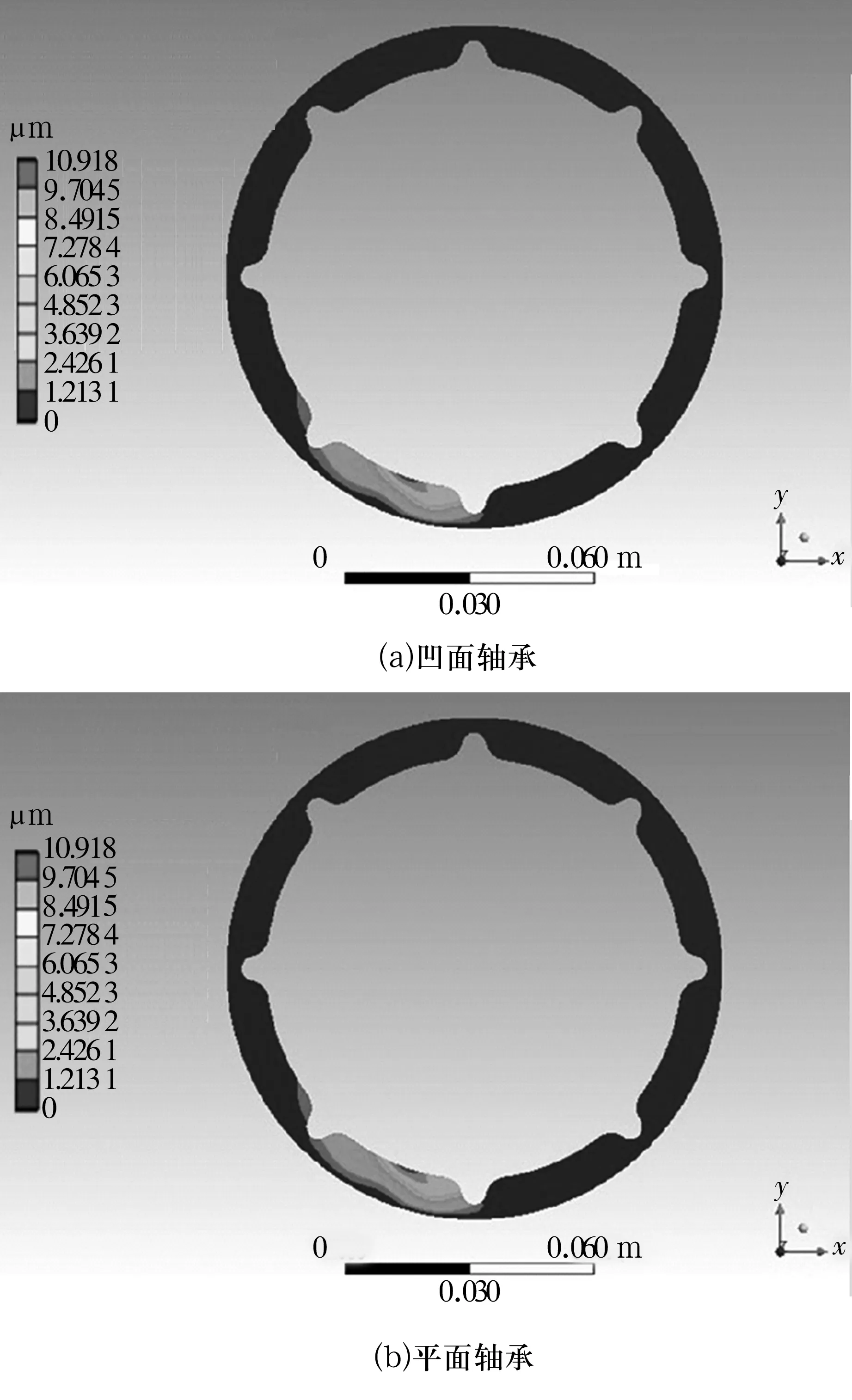
图12 橡胶变形分布云图Fig.12 Deformation distribution nephogram of rubber

水囊增加了水膜厚度，改善了轴承润滑条件，促进了流体压力形成；但随着橡胶变形量增加，轴与橡胶轴承之间会产生接触与摩擦，从而使橡胶轴承工作状况恶化，不利于润滑膜形成。平面轴承的板条变形主要发生在两端(图12b)，这是由于平面轴承板条与轴之间形成了先收敛后发散的水膜间隙，从而在板条上形成了2个相互独立压力峰，因此板条上出现2个凹陷。

由于凹面轴承和平面轴承在橡胶变形量、最小水膜厚度与转速的变化关系类似，因此以下仅以凹面轴承为例进行分析。凹面轴承橡胶变形量与刚性轴承最小水膜厚度随转速变化曲线如图13所示。由于橡胶变形量与最小水膜厚度可采用同一单位(mm)，且变化范围相近，因此在同一图中表示。由图13可知，载荷一定时，随着轴转速增加，橡胶变形减小，水膜厚度增大。当载荷为800 N、转速为60 rad/s时，橡胶变形量为0.762 mm，已经远大于刚性轴承在此工况下的最小膜厚度0.080 8 mm，说明此时轴承将与轴发生接触；当转速为200 rad/s时，橡胶变形量为0.307 mm，刚性轴承最小水膜厚度为0.356 4 mm，大于橡胶变形，说明此时轴承可以形成连续水膜。因此，橡胶变形量随着转速减小和载荷增加而增大，降低转速或增加载荷都会引起轴与轴承接触。

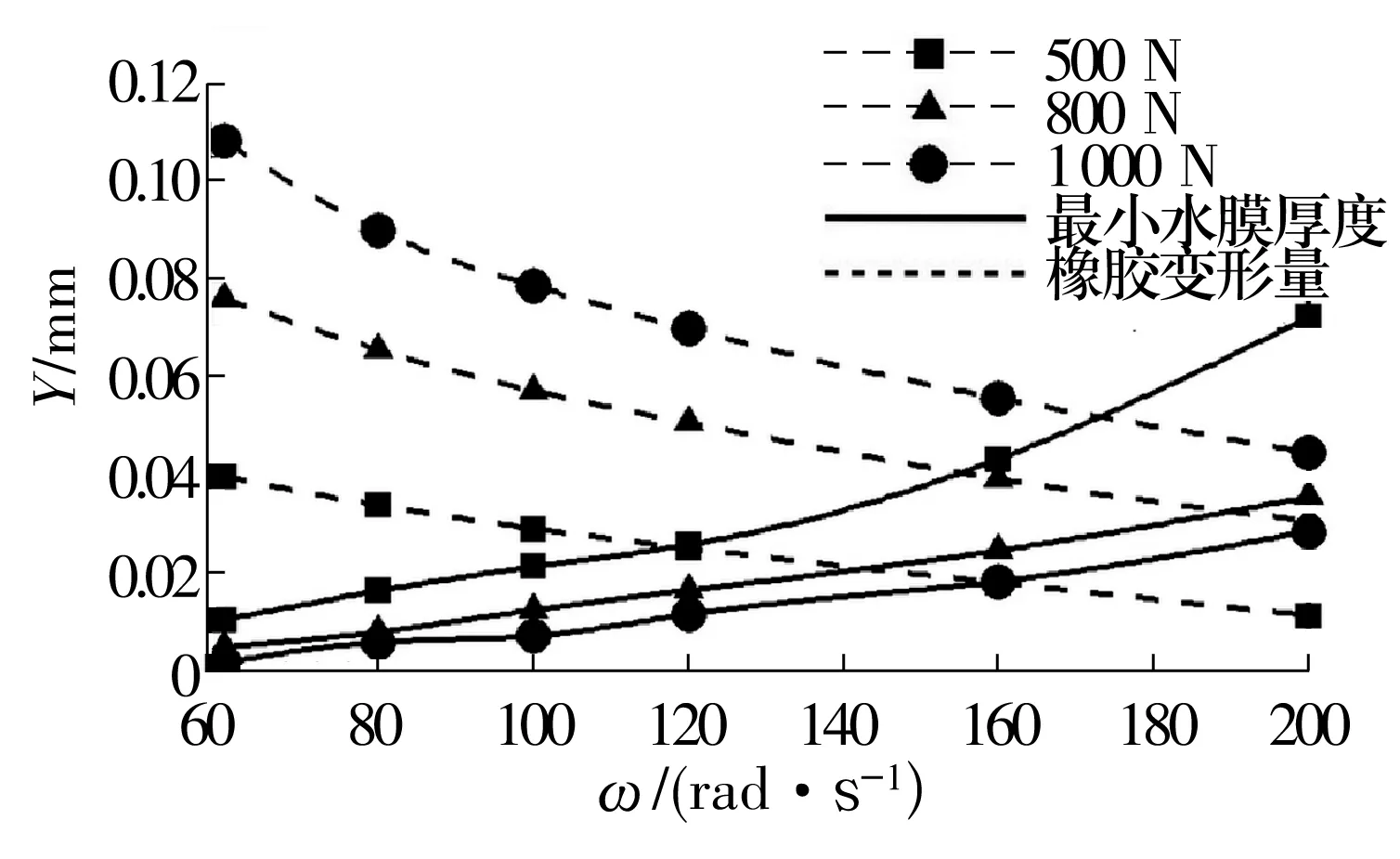
图13 橡胶变形量与最小水膜厚度随轴转速变化曲线Fig.13 Variation curves of rubber deformation and minimum water film thickness with shaft speed

凹面橡胶轴承与刚性轴承最大水膜压力随轴转速的变化曲线如图14所示。由图可知，橡胶轴承的最大水膜压力随着轴转速的增加而减小，随着载荷的增加而增大；转速越大，橡胶轴承最大水膜压力与刚性轴承的越接近，这是由于最大压力减小，导致橡胶变形减小。相同工况下，橡胶轴承水膜压力变化幅度小于刚性轴承；由于橡胶变形导致水膜承载面积增大，因此与刚性轴承相比，橡胶轴承水膜压力低，但水膜厚度大。

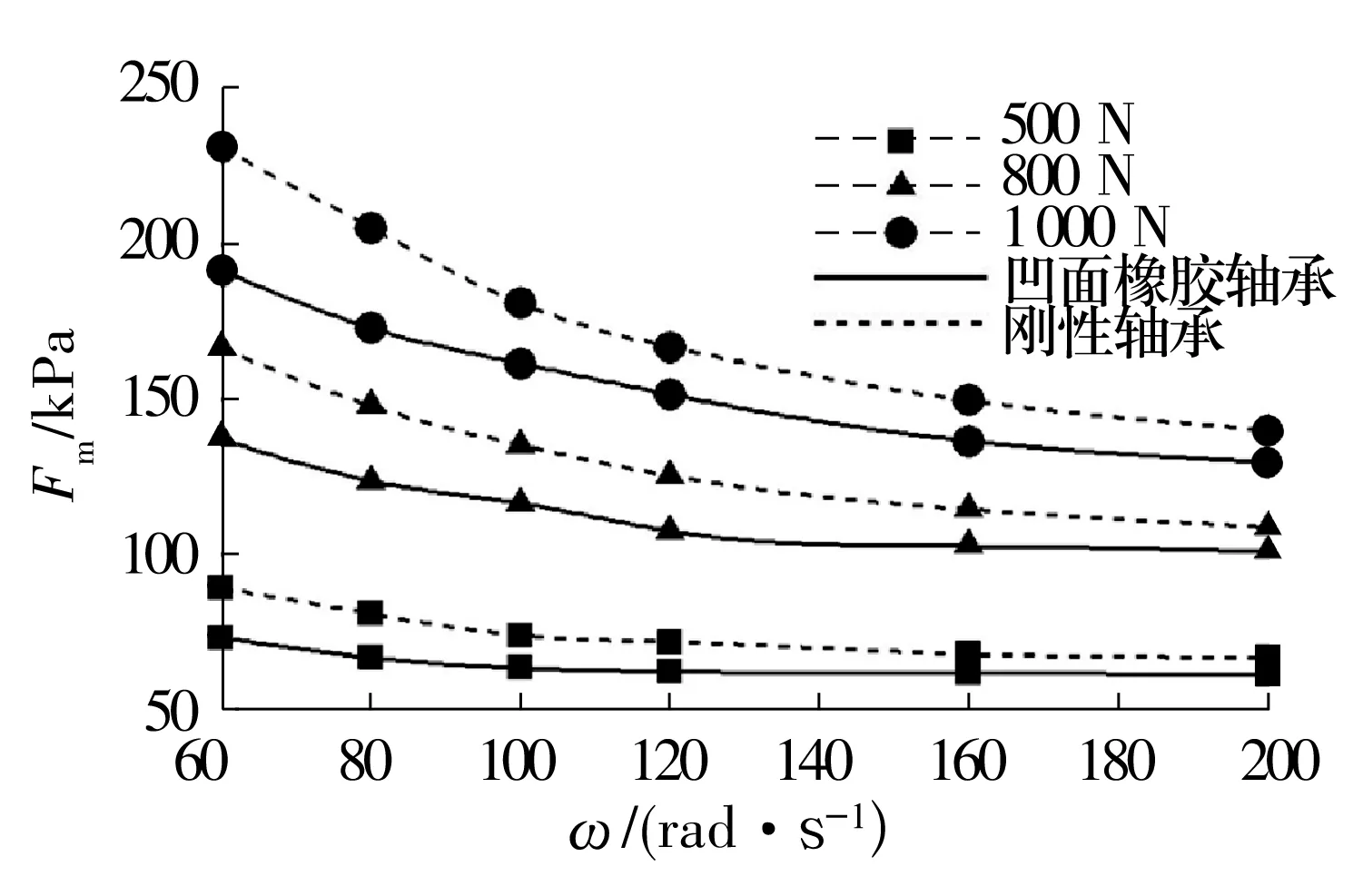
图14 轴承最大水膜压力随轴转速的变化曲线Fig.14 Variation curres of maximum water film pressure of bearing with shaft speed

4 水膜压力测试试验

4.1 试验方法

应用无线传感技术在水润滑轴承试验台上对2种轴承进行水膜压力测试试验[15]，传感器布置方案如图15所示，试验轴承的8个板条(stave1～stave8)与水膜压力测试传感器分别编号，轴顺时针旋转。键相信号传感器位于水平位置，即传感器1在板条1位置，确定轴承位置后，只要获取键相信号，即传感器1的位置确定，则可确定其他传感器位置，可得每个传感器所测得的水膜压力在对应板条上的分布情况。试验工况与仿真条件设置如下：径向载荷0～1 000 N(比压0～0.024 MPa)，轴转速240～1 920 r/min(25～201 rad/s)，供水压力0.1～0.6 MPa；无线采集发射装置参数为：波特率9 600 bits/s，无线采集发射装置DSP采样频率1 024 Hz，采样点数256，每次传输数据量32字节。在水膜压力测试前，对整个水润滑轴系进行对中及平衡调整。

图15 传感器布置方案Fig.15 Layout scheme of sensors

4.2 结果与分析

轴转速960 r/min(100 rad/s)、供水压力0.3 MPa时，传感器3测得的2种轴承全周水膜压力分布如图16所示。由图16a可知，轴承均出现负压，但凹面轴承负压出现在板条1处，因此凹面轴承在承载区(周向角为210°～330°)存在连续水膜，但过了承载区水膜开始破裂，这与图9a偏心率为0.8时的水膜压力分布仿真结果基本一致；由图16b可知，平面轴承在每个板条都有独立压力峰，且负压区域较大，表明平面轴承在承载区不能形成连续水膜，与图9b中仿真结果也基本一致。

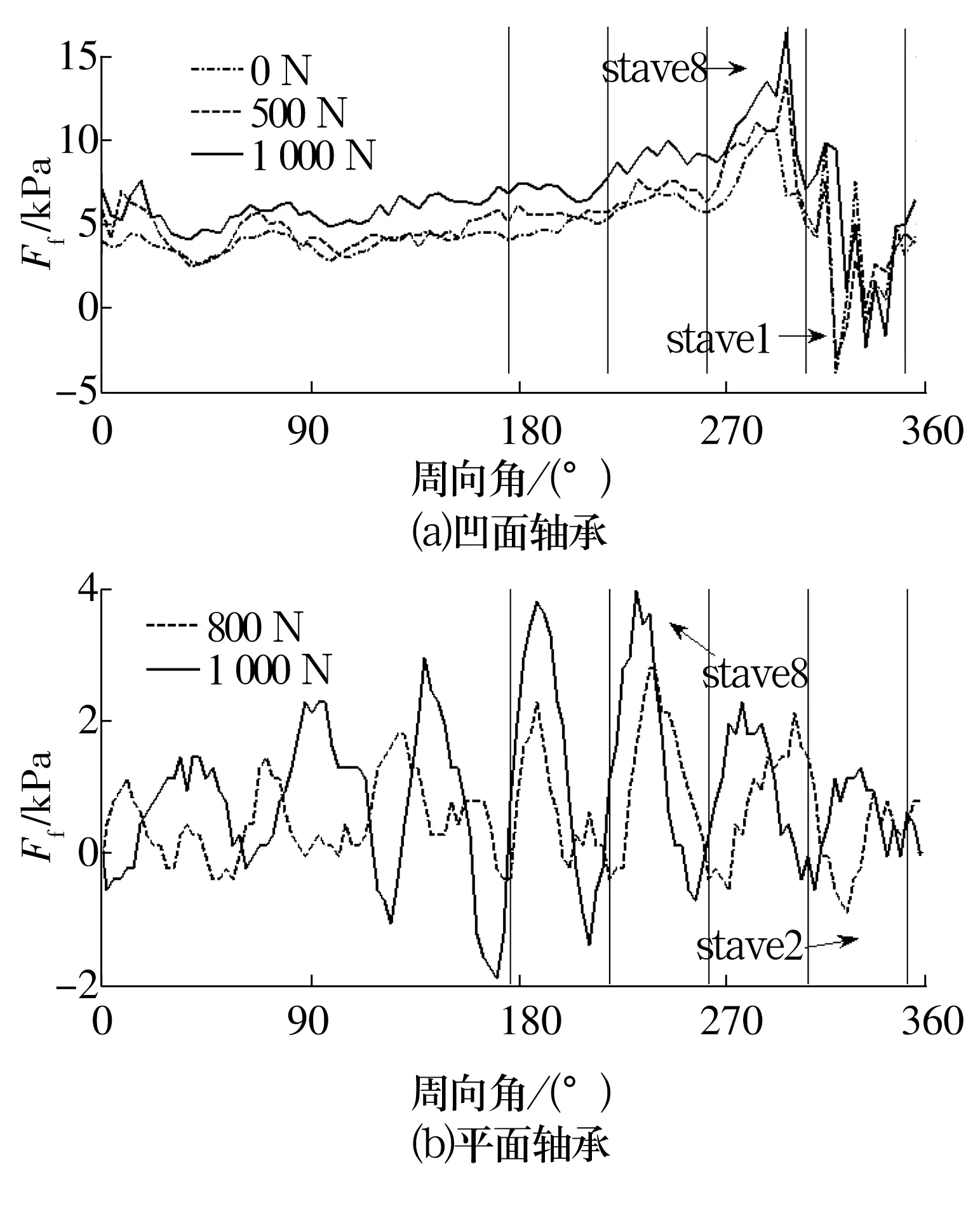
图16 轴承周向连续水膜压力分布曲线Fig.16 Circumferential continuous water film pressure distribution curves of bearings

综上所述，平面轴承形成的流体压力及承载能力远小于凹面轴承，这是由于平面轴承每个板条上都同时存在一个小的收敛、扩散楔形，而凹面轴承存在一些板条，其收敛楔形宽于或等于板条宽度。此外，平面轴承收敛楔形入口高度较大，凹面轴承收敛楔形入口高度较小，平面轴承收敛楔形由较大入口高度在较窄范围内很快减小到出口高度，而凹面轴承收敛楔形由较小入口高度在较宽范围内缓慢减小到出口高度，狭长收敛楔形使凹面轴承更易于形成流体压力。凹面轴承可能形成宏观尺度润滑膜，但不能形成完全润滑膜将轴与轴承全部隔开，因此凹面轴承在摩擦界面上既存在连续润滑膜又存在宏观尺度的直接接触，属于混合润滑状态；而平面轴承不能形成流体膜，属于边界润滑状态。

5 结论

1)载荷不变时，增加轴转速会使轴承偏心率减小，最小水膜厚度增加；轴转速增大到一定程度后，轴承将与轴产生接触；长径比越大，轴承偏心率越小，越不易与轴产生接触。

2)凹面轴承承载区基本无空化现象，平面轴承空化现象较严重，凹面轴承承载力优于平面轴承，平面轴承更易与轴产生接触；橡胶变形产生的水囊可增加水膜厚度，改善轴承润滑条件，但其变形量不断增加将导致轴与轴承产生接触与摩擦，使轴承工作状况恶化；凹面轴承处于混合润滑状态，平面轴承处于边界润滑状态。

3)橡胶变形量随着转速减小、载荷增加而增大；相同工况下，与刚性轴承相比，橡胶轴承的水膜压力变化幅度小，水膜压力低，但水膜厚度大。