FDD大规模MIMO系统速率最大化导频信号设计方法

王 毅 冀保峰 张松炜 闫利超 郭 慧 李春国 杨绿溪

(1. 郑州航空工业管理学院电子通信工程学院， 河南郑州 450046；2. 国家数字交换系统工程技术研究中心， 河南郑州 450002；3. 河南科技大学信息工程学院， 河南洛阳 471023； 4. 东南大学信息科学与工程学院， 江苏南京 210096)

1 引言

大规模多输入多输出(Massive MIMO)技术利用在基站部署的巨量天线阵列，获得了相较传统MIMO系统诸多不同的特性，特别是频谱效率、能量效率、发送/接收机线性化操作、空间波束分辨率、空口延时和物理层控制信令开销等方面取得了显著的性能提升[1-3]。正因为如此，业内普遍认为未来5G移动通信系统关键性能指标的实现有赖于大规模MIMO这一物理层关键技术的突破[4- 6]。

然而，大规模MIMO技术的优异性能是以基站获取可靠有效的信道状态信息(Channel State Information, CSI)为前提，而CSI的精确程度也直接决定了系统的下行空间波束复用、资源分配、检测接收等环节的性能[7- 8]。对于目前占主流的频分双工(Frequency Division Duplexing, FDD)制式蜂窝系统而言(全球范围内4G LTE FDD牌照超过300张，而时分双工(Time Division Duplexing，TDD)牌照仅有40余张[9])，由于FDD制式中上下行信道不满足互易性，必须通过基站发送下行导频信号，在用户侧进行信道估计，进而反馈至基站再进行相应的预编码或波束成型方案设计[2]。由于基站配置了大规模天线阵列，采用下行正交导频序列时，其导频长度将会随着天线数增加而成倍增加，从而导致消耗较大的系统资源，影响整个系统的频谱利用率[7]。与此同时，业内考虑到从4G FDD系统到5G系统的平滑过渡以及5G系统后向兼容性，必须着力解决FDD大规模MIMO系统中的导频开销及导频设计问题，这对于FDD制式下大规模MIMO技术的应用推广具有重要的现实意义[9]。

文献[10]研究了非正交条件下的导频设计问题，利用信道反馈信息对导频序列进行迭代优化。文献[11]联合考虑了信道的空时两维度相关性，借助于信道的时间相干性进行信道预测，进而设计了开环和闭环条件下的低开销导频和信道估计方案。文献[12]挖掘信道空间相干性，以经典的信道估计均方误差最小化为目标，对导频信号进行优化设计。文献[13]则利用信道时间相关性和卡尔曼滤波器，并考虑低实现复杂度的有限射频链路(Radio Frequency Chain, RF Chain)预编码方案，设计了一种低开销的周期性训练序列发送方案。以上研究都考虑的是单用户场景下的导频设计，这是由于普通的多用户场景下用户的信道空时相关性各异，而基站发送的下行导频是一致的，因此，无法使得单一导频矩阵匹配所有用户的信道特性。正如文献[14]所述，针对FDD大规模MIMO系统多用户普适场景下的导频设计问题仍是一个开放性热点问题，所以，现有的研究中多数是基于单用户场景或者具有某种特性信道条件的多用户场景。文献[15]就是通过对具有相同信道空间相关阵的多个用户进行分组，在特殊的多用户场景下，提出一种基于块迫零的两级预编码方案。通过假设组间用户的协方差阵正交性，利用第一级预编码进行组间干扰抑制，从而降低组内用户的有效信道维度，从而减少可能的导频开销并简化预编码设计。然而，文献[15]的重点在于两级预编码方案设计，而未给出相应的导频优化设计方案。

另外值得注意的是，上述针对FDD大规模MIMO系统的导频设计方案，仍是以信道估计的精确程度为准则，即信道估计均方误差，由此来设计低开销的导频方案。然而，导频信号除了影响信道估计精度外，还将间接的影响基站下行波束向量的设计和信道匹配问题，进而影响系统的传输速率。与此同时，导频信号所消耗的时长资源影响着后续的有效数据发送时长，也就会对系统的有效传输速率产生作用。而传输速率是通信系统所关注的重要指标，也直接反应系统性能的好坏。因此，以系统有效传输速率作为准则来优化设计导频信号具有更实际的意义。而目前，尚未见到有针对FDD大规模MIMO中基于传输速率的导频设计方案。

基于上述分析，本文着眼于单用户FDD大规模MIMO系统中的导频信号设计问题。利用信道空间相关性，并结合信道估计和数据波束成型发送对导频信号设计的影响，以系统下行遍历可达速率为优化目标，并考虑系统总功耗约束，来优化设计导频信号矩阵。由于优化问题的代价函数无解析表达式，借助于确定性等价方法，推导得出精确地近似闭合表达式，从而显式的描述遍历速率与导频信号的数学关系。基于此，进一步推导出了最优导频信号的矩阵结构特征，从而将原优化问题转换为等价的导频功率分配问题。再利用拉格朗日对偶法，获得了最优导频信号的解析形式解。最后，通过数值仿真验证了所提出的速率最大化导频方案的有效性。

文中符号说明：(·)H表示矩阵的共轭转置。Tr{·}表示矩阵的迹。{·}表示统计期望运算。diag{a}表示以向量a为主对角元素构成的对角阵。表示服从均值向量为n协方差阵为R的循环对称复高斯随机分布。|·|，‖·‖和‖·‖0分别表示模运算，Frobenius范数和0范数。R(i,j)表示矩阵R的第i行第j列元素。rank(R)表示矩阵R的秩。

2 系统模型

考虑如图1所示的单用户FDD大规模MIMO下行链路传输系统，其中，基站配置大规模天线阵列，且天线数为N≫1，用户配置单天线[10-12]。假设基站到用户之间的信道满足瑞利平坦衰落，且信道相干间隔(channel coherent interval)为Tc(以符号长度计)，即信道系数在Tc时长内保持准静止，而在不同的相干间隔块内独立变化[11]。在FDD制式下，基站需要通过下行信道估计、上行信道信息反馈和数据波束成型三个过程来完成下行链路数据传输[11,16]。

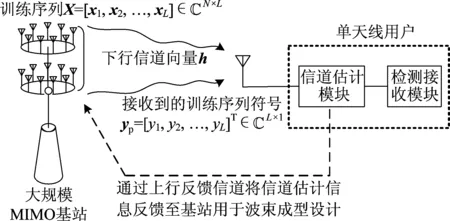
图1 FDD大规模MIMO下行链路系统Fig.1 FDD massive MIMO downlink system

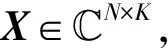
yp=XHh+np

(1)

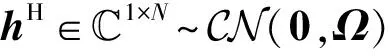
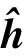
(2)

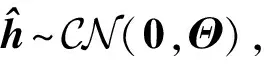
根据MMSE估计的正交性原理[18]，可将信道向量h分解为

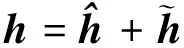
(3)

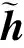
用户获得CSI估计值后，将其通过上行信道反馈至基站处。由文献[11]和文献[15]可知，在反馈信道条件较好时，即反馈信道处于发高射信噪比时，由反馈量化等因素带来的误差相对于信道估计误差是可忽略的。由于本文着眼于基站侧的联合信道估计与下行波束成型两个阶段对导频设计的影响，此处考虑完美的反馈信道条件，即零延迟和零误差反馈信道，从而忽略反馈阶段造成的影响，由此，基站可获得精确的信道估计向量值[11,16]。

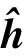
(4)

其中，ρd表示有效数据符号的发射功率，s表示具有单位功率的有效数据符号，即表示波束成型向量，且满足功率归一化表示数据发送阶段用户端受到的复加性高斯白噪声。

由于用户无法获知信道估计误差，根据最差情况不相干加性噪声理论[18]，根据式(4)可以得到用户的接收信噪比为

(5)

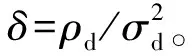
(6)

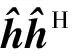
(7)

显然，式(7)右边为标准的瑞利瑞兹比形式。利用文献[21]中类似的方法，可以直接得到最优波束成型向量与对应的最大接收信噪比分别为

(8)

(9)

由此，可以得到下行链路的遍历可达速率为

R=

(10)

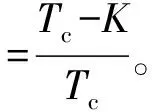
结合式(2)和式(10)可以看到，导频信号不单影响信道估计精度性能，更直接影响着波束向量与信道的匹配程度以及由此对系统可达速率造成的影响。基于此，以系统可达速率为目标，并考虑发射功率约束，建立关于导频信号的数学优化模型，如下所示，

s.t. Tr(XXH)≤P

(11)

3 速率最大化导频信号设计方法

3.1 遍历速率解析表达式

对于式(10)中的遍历速率表达式，其期望运算通常是非常困难的。然而，借助于大维随机矩阵理论中的确定性等价方法[18]，可以获得遍历速率的一种精确近似闭合表达式，如引理1所述。

引理1 当基站采用式(8)中MRT波束成型向量进行下行数据发送时，用户端的下行遍历速率具有如下近似解析表达式，

(12)

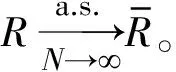
证明过程参见附录。

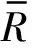
将式(12)代入式(11)中优化问题目标函数，可以得到近似等价的优化问题，如下所示

s.t. Tr(XXH)≤P

(13)

3.2 导频优化算法设计

由于优化问题(13)中变量为矩阵，且函数形式较为复杂，不便于判断凹凸性，因而，无法直接利用标准的凸优化方法进行求解。然而，根据主导理论[22]，可首先推导得出最优导频信号所有的矩阵结构，如定理1所述。

定理1 若优化问题(13)存在最优解Xopt，则该最优解具有如下形式，

Xopt=UQ

(14)

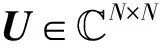
证明：将Ω=UΛUH代入式(13)中的目标函数并化简，可以得到

(15)

(16)

(17)

由于矩阵Z是对角阵，且其对角元素降序排列。当且仅当矩阵V为对角阵，且其对角线元素的顺序与矩阵Z对角阵元素顺序相反时，即V对角线元素为升序排列，才能达到式(17)的上界[22]。因为S为对角阵，且对角线元素升序排列。因此，D=UHXXHU必是对角阵，且其对角线元素为降序排列。又因为rank(D)≤m，由此可得D具有如下形式，

(18)

对D进行平方根运算，并构造矩阵Q如下所示，

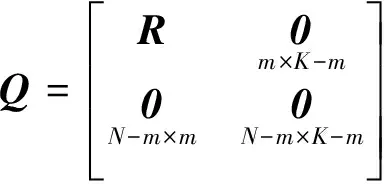
(19)

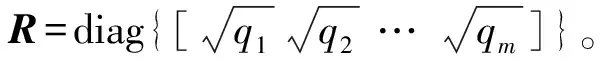
由此可以得到，

X=UQ

(20)

证毕。

进一步，利用定理1中导频结构特性，并进行变量替换，可将优化问题(13)中的导频信号设计问题等价转化为导频序列的功率分配问题，如下所示，

(21)

根据文献[23]中关于函数凹凸性的定义，容易验证(21)中目标函数关于变量q是凹的，且当约束条件取等号时使得目标函数达到最大值。因此，可利用拉格朗日对偶法求解该问题。由式(21)中目标函数可得拉格朗日对偶函数为

(22)

其中，μ为非负的拉格朗日乘子，对应于发射功率约束项。

(23)

(24)

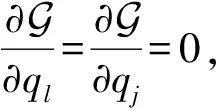
(25)

进一步化简式(25)可以得到，

(26)

将式(26)代入式(23)的右侧等式，合并化简后可以得到

(27)

再根据二次方程的求根公式可以直接得到方程(27)的解为

(28)

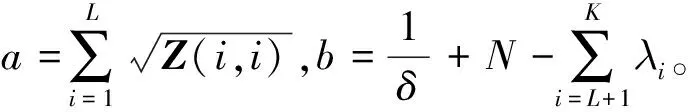
(29)

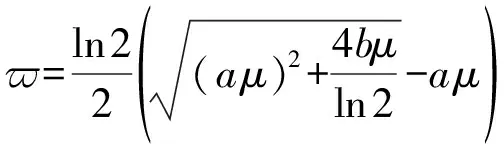
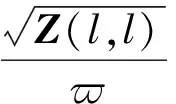
同时，在进行导频序列功率分配后，其最终使用的导频序列长度应为‖q‖0，比预设的导频序列长度可能会缩短，即‖q‖0≤K。这主要是因为导频信号所使用的功率受制于系统的总功率约束。而从式(29)中也可以看到，在某些情况下，某些信道子特征方向上分配的导频序列上功率值可能为0。然而，通常情况下，只有通过导频功率分配后才能得到‖q‖0。另一方面，尽管无法预先获知‖q‖0的值，但是，结合定理1推导过程及式(19)和式(20)可以发现，满足优化问题(13)中的导频序列的最大长度(即Xopt的列维度)应是小于等于N的。换句话说，在进行导频长度预设时，只需设定K≤N即可。从物理意义上来讲，由于下行信道向量存在于N个信道特征子方向构成的特征子空间，因此，其所需要的导频序列长度只需要对准这N个子特征方向进行即可，而无需使用更长的导频序列。

最终，根据经典功率注水算法[23]，可以得到基于速率最大化的导频信号设计算法的具体流程如下：

步骤1 初始化：计数变量n=1;

步骤2 Repeat;

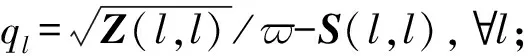
步骤5 IFqm-n+1<0;

步骤6qm-n+1=0；

步骤7n=n+1；

步骤8 ENDIF;

步骤9 Untilql≥0,∀l。

4 仿真结果与分析

本节将给出不同系统参数设置下，基于遍历速率最大化的导频方案的传输性能情况。为便于仿真并不失一般性，对系统参数做如下假设：基站到用户的大尺度衰落因子归一化为1，信道估计阶段与数据传输阶段的加性高斯白噪声功率归一化为1 W，信道相干间隔Tc=40，预设导频序列长度K=10。对于信道相关矩阵Ω，此处采用满足均匀线性天线阵列特性的指数衰减型模型，即Ω(i,j)=r|i-j|，(i,j=1,…,N)，其中，r∈(0,1)称为信道空间相关性系数，用来表示信道的空间相关性强弱[16,24]，即信道相关性越强，r的取值越大，反正，r的取值越小。为了便于对比，给出两种常用准则下的资源分配算法：为了便于比较，以文献[17]中基于最小化MSE的导频方案和文献[16]中的等功率分配正交导频方案为基准，进行性能比较。

图2通过蒙特卡洛数值仿真验证了本文引理1中给出的遍历速率解析表达式的近似程度与精确性。由于引理2中涉及的导频信号是任意形式的信号矩阵，为了便于仿真，此处采用大规模MIMO系统中常用的列正交等功率导频矩阵，且蒙特卡洛数值结果是由5000次独立信道生成后取平均得到。从图中可以看到，随着天线数的增加，遍历速率解析表达式所得到的近似值将越来越逼近于真实值，这表明采用该闭合表达式设计导频信号具有有效性和精确性。

图3给出了三种导频方案下信道估计的归一化均方误差性能。首先，在不同的信道相关性条件下，基于MSE最小化的导频方案所获得信道估计性能始终是最好的，基于等功率分配正交导频的方案性能居中，且其与MSE最小化导频方案的性能差异相对较小，特别是在总功率较大时，二者几乎重合，与文献[17]中的结论一致。这是由于高发射功率区间，最小化MSE导频方案就趋近于等功率分配。而本文所提出的导频方案则在信道估计精度方面略差，特别是在强相关信道条件下，性能损失较为严重。其次，进一步观察可以发现，在弱相关信道条件下，三种导频方案的信道估计MSE性能差异很小，并且整体的信道估计精度相对于强相关信道条件下都大为降低。这主要是由于弱相关信道条件下，信道各个特征子方向上的强度趋于相同，想获得好的精度则需要更长的导频序列对准到各个特征子方向上。相对于强相关信道而言，在有限的导频长度和总功率约束下，其所能获得信道估计精度就会受到较大影响。最后，随着总功率的增加，三种导频方案的信道估计精度都变得越来越好，并且在高信噪比时，三种方案的MSE性能达到一致。

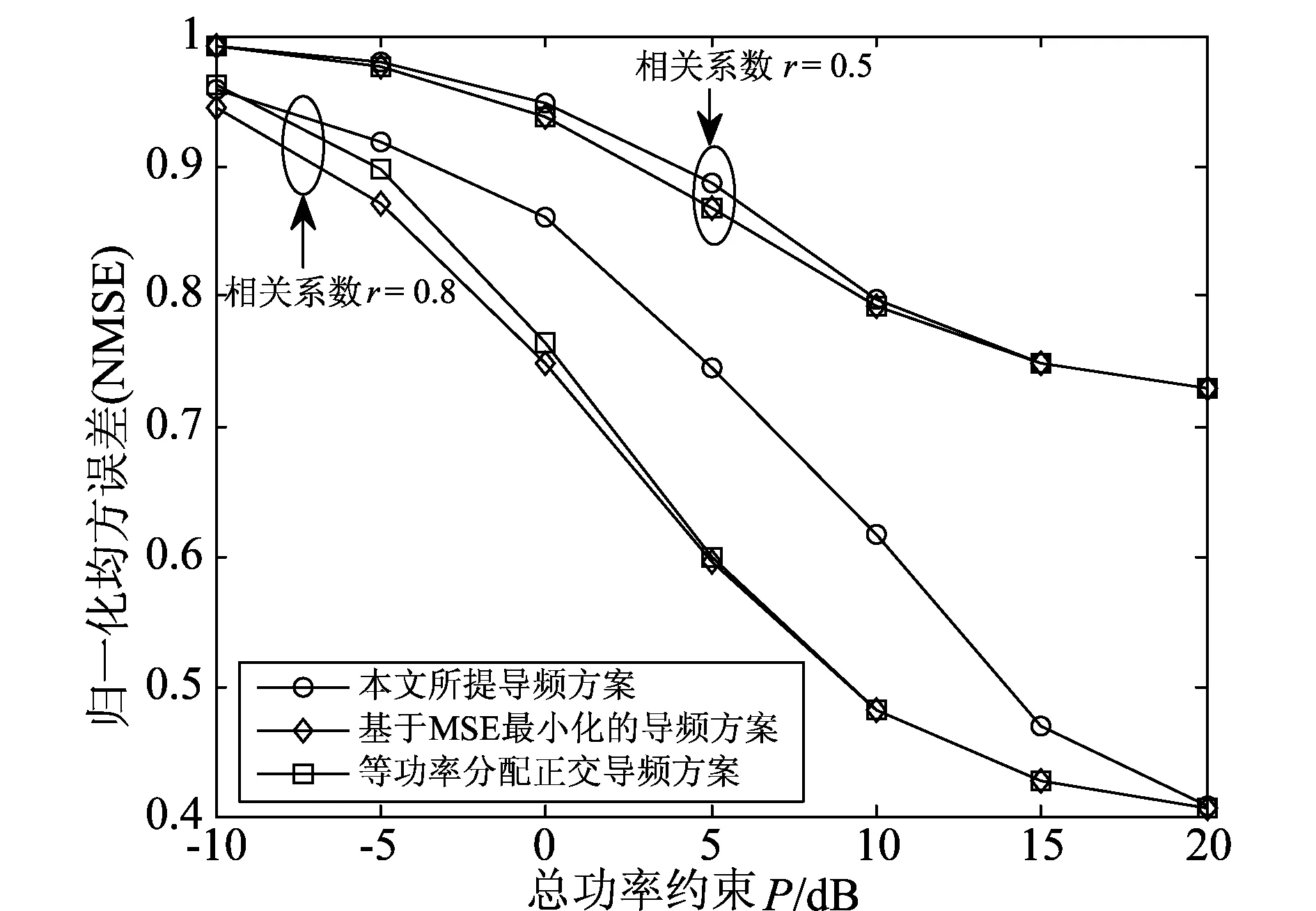
图3 不同导频方案下的归一化均方误差性能对比(N=100,ρd=10 dB)Fig.3 Comparison of normalize mean square error (NMSE) performance with different pilot schemes (N=100,ρd=10 dB)

图4描述了三种导频方案的下行遍历可达速率随总功率约束的变化趋势对比。从图中可以看出，本文所提出的导频方案具有最优的性能，特别是在强相关信道下以及总功率处于中低值区间时，本文所提方案的遍历速率的优势更加明显。然而，对比图3会发现，在强相关信道条件下，本文所提导频方案的信道估计精度却远差于其他两种导频方案。本文所提方案在由较差的信道估计值条件下，却带来了较好的可达速率性能，而这主要归功于本文所提方案在导频序列功率分配上的特性以及实际的导频序列占用长度。具体在于：强相关信道下，信道增益主要分布在少数几个强特征方向上，即若干少量的特征值占据了整个信道增益的较大比例。因此，在本文所提的导频方案中，给出的导频序列功率主要集中在少量的特征方向上，并且使用了较少的导频序列长度，也正是如此，使得一个相干间隔内有更多的符号用于发送有效数据。结合图5与图6可以清晰看到，在总功率P=-10 dB和0 dB时，本文所提方案中的导频序列长度分别为1和2，而此时MSE最小化的导频方案却使用了长度为4和9的导频序列。值得注意的是，随着信道相关性的减弱，三种导频方案下的遍历可达速率绝对值均有所下降，这主要是由于有限的导频序列长度和总功率约束，使得三种导频方案获得的信道精度均大为下降，也削弱了本文所提导频方案在可达速率方面的性能增益。综上所述，本文所提方案以较少的信道估计精度损失，带来了较好的遍历可达速率增益，具有更好的使用价值，特别是在强相关信道下具有更强的应用场景。

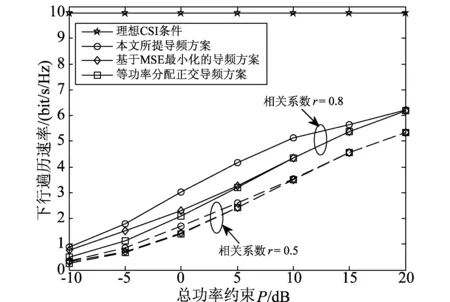
图4 不同导频方案下的下行遍历可达速率性能对比(N=100,ρd=10 dB)Fig.4 Comparison of downlink ergodic achievable rate performance with different pilot schemes (N=100,ρd=10 dB)

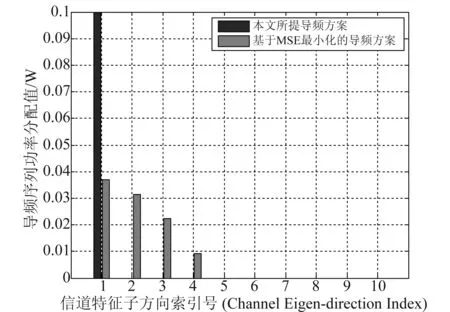
图5 总功率约束P=-10 dB时，导频序列对应于信道特征子方向上的功率分配(N=100,ρd=10 dB)Fig.5 Power allocation for different channel eigen-directions with total power constraint P=-10 dB (N=100,ρd=10 dB)

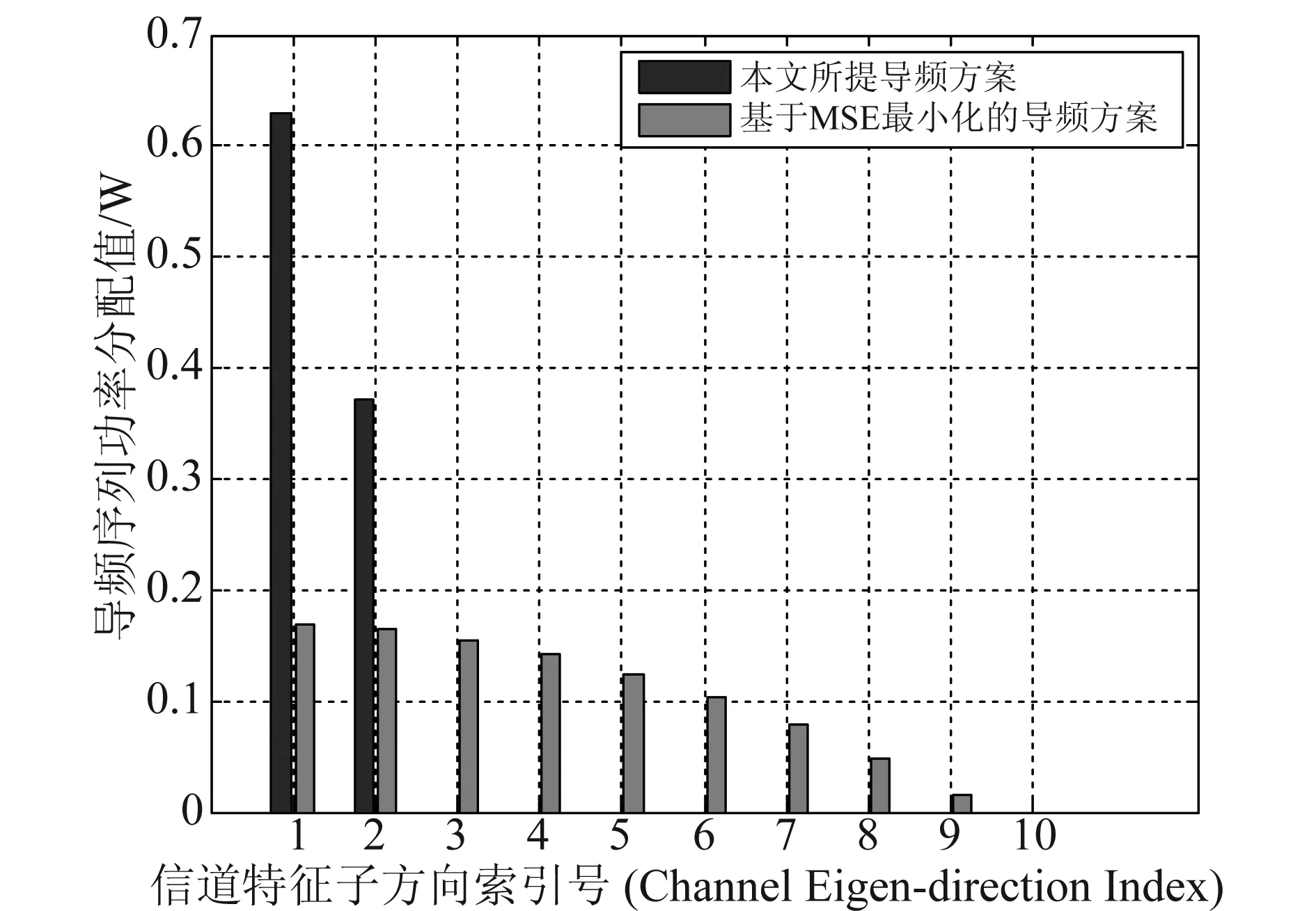
图6 总功率约束P=0 dB时，导频序列对应于信道特征子方向上的功率分配(N=100,ρd=10 dB)Fig.6 Power allocation for different channel eigen-directions with total power constraint P=0 dB (N=100,ρd=10 dB)

图5至图8展示了不同总功率约束条件下，导频序列对应在不同的信道特征子方向分配的功率值。从图中可以看到，两种导频方案均是在信道的强特征子方向上分配更多的功率，而弱信道特征方向上分配较少甚至为零功率。然而，所不同的是，本文所提出的导频方案，在总功率较小时，会使用更少的导频序列长度，而将功率尽可能多的分在强特征方向上。特别是在图5中，本文所提导频方案仅使用了一个导频序列符号，并且将功率全部分配于该方向上，主要是为了在波束成型阶段将功率匹配到最强的信道特征方向上，从而可以获得更好地波束成型增益。尽管这样做会对信道估计精度带来一定影响，但是，从另一个角度来看，在一个信道相干间隔Tc内，导频长度的减小则意味着留出了更多的时长资源用于发送有效数据，从而对整个系统的有效数据传输速率是有益的。随着总功率约束的增加，可以看到，基于MSE最小化的导频方案则趋于等功率分配，而本文所提导频方案则始终呈现出明显的阶差功率分配特性。同时，两种导频方案随着总功率约束的增加，可使用的导频序列长度也在逐渐增加。但是，本文所提方案中，导频序列的实际使用长度随着总功率约束呈现缓慢增加的趋势，而MSE最小化准则下的导频方案，则是将有限的功率分配在尽可能多的导频长度上。由此说明，不同的导频设计方案下，导频序列长度与实际系统的总功率有着迥异的关系。

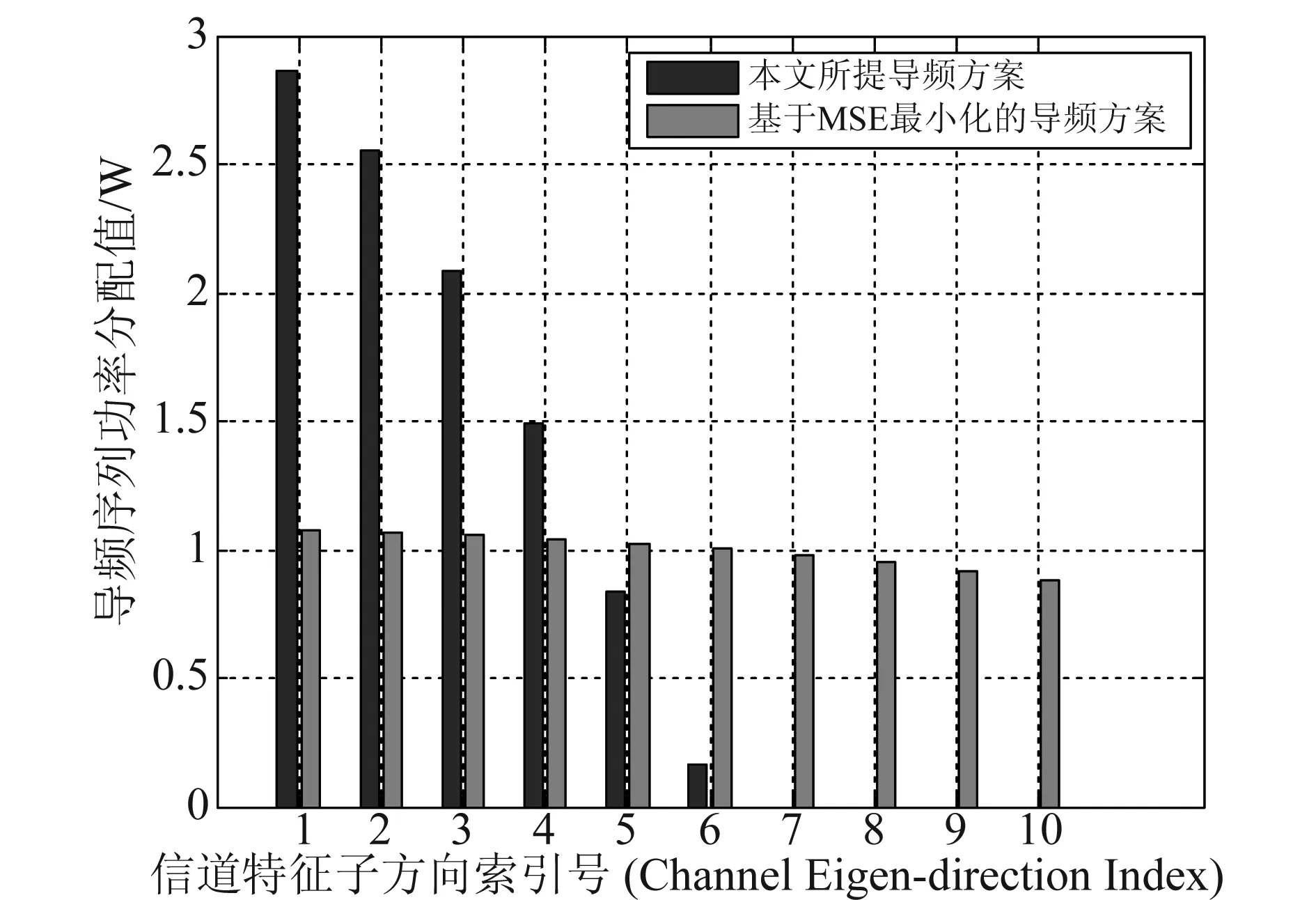
图7 总功率约束P=10 dB时，导频序列对应于信道特征子方向上的功率分配(N=100,ρd=10 dB)Fig.7 Power allocation for different channel eigen-directions with total power constraint P=10 dB (N=100,ρd=10 dB)

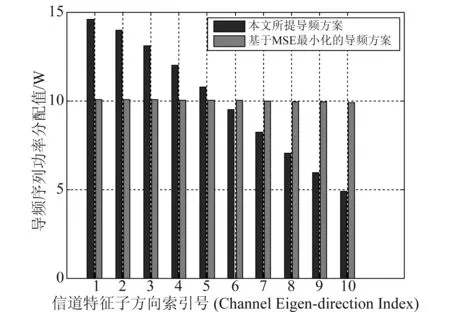
图8 总功率约束P=20 dB时，导频序列对应于信道特征子方向上的功率分配(N=100,ρd=10 dB)Fig.8 Power allocation for different channel eigen-directions with total power constraint P=20 dB (N=100,ρd=10 dB)

5 结论

本文针对FDD大规模MIMO系统，联合考虑信道空间相关性、信道估计进行以及下行波束成型方案对导频信号设计过程中的影响，提出了一种以下行遍历可达速率最大化为目标、以系统总功耗为约束的导频信号优化方法。由于原始优化问题的代价函数无精确解析形式，无法显示的表达遍历速率与导频矩阵变量的关系，根据确定性等价原理推导得出了遍历速率的闭合形式表达式，从而定量的描述遍历速率与导频矩阵的数学关系。基于此，通过主导理论，推导出了最优导频信号的矩阵结构特征，即列正交特性。该结构特性与基于最小均方误差最小化的导频方案具有类似的结构特性，也就是将导频序列对准信道子特征方向。进而，利用该导频的结构特性，将原优化问题转换为关于导频序列的功率分配凹问题，再利用拉格朗日对偶法，得到了最优导频信号的解析解。从该最优解表达式可以看到，所提出的导频功率分配具有多级水平线注水特点，即针对不同强度的信道特征子方向，划定不同的注水线。数值仿真结果首先验证了遍历速率闭合表达式与理论值的近似逼近程度，进而与基于最小均方误差准则导频方案和等功率正交导频方案进行了性能比较，分析了其性能增益的主要原因。

附录

引理1证明

由于用到大维矩阵理论中的渐进性分析，根据文献[18]和文献[24]所述，假设信道相关阵Ω具有一致有界谱范数。进而，根据文献[25]引理1(或文献[18]引理4)，可以得到接收信噪比的确定性等价近似量为

(30)

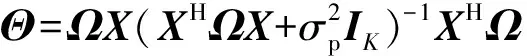
(31)

进而，利用主导收敛和连续映射理论[18]，可以得到式(10)中下行遍历可达速率的确定性等价近似值为

(32)

证毕。