频分MIMO雷达分解迭代稳健自适应波束形成算法

李星星 向 龙 熊智敏 王党卫 马晓岩

(空军预警学院, 湖北武汉 430019)

1 引言

2006年,P.Antonik等学者首次提出了频率分集阵列(Frequency Diversity Array,FDA)雷达的概念[1],国内也称之为频控阵雷达[2],其可通过阵元间附加小的频偏控制实现距离-角度依赖波束。受益于这种独特波束,FDA雷达较传统相控阵和多输入多输出(Multiple Input Multiple Output,MIMO)雷达在波束综合[3- 8],高分辨成像[9-10],目标定位[11-14],距离模糊杂波和干扰抑制[15-16]等方面提供了更优的性能。

自适应波束形成作为该雷达研究中的难点问题,一直受到国内外学者的关注[17-19]。为降低波束域距离-角度耦合,文献[16]将FDA和MIMO技术结合起来并称之为FDA-MIMO雷达,该体制能同时利用FDA的距离波束特性和MIMO雷达的收发分集特性。文献[17]研究了基于MVDR的频率分集MIMO相控阵雷达距离依赖波束形成,理论上证明了该体制雷达较传统MIMO和相控阵雷达具有更优的波束性能;文献[18]分析了FDA-MIMO雷达频率增量误差对波束性能的影响,文献[15]对FDA-MIMO雷达距离欺骗干扰抑制问题进行了研究,且将最差性能最优波束形成算法扩展到该体制;而文献[19]则进一步将线阵FDA波束形成理论扩展到面阵并分析了其常规波束形成性能。虽然上述成果对FDA-MIMO雷达波束形成进行了较为深入的研究,但只考虑了回波数据包含信号的情况,并没有研究如何抑制目标到达角、阵列位置、幅相等误差对输出SINR带来的不利影响,而且对于如何解决距离波束栅瓣引起的周期性输出信干噪比(SINR)损失问题亦未深入。

为了提高频率分集雷达体制自适应波束形成的稳健性,本文在文献[15]和文献[19]的基础上,提出了一种频分子孔径MIMO雷达(Frequency Diverse Subaperturing MIMO,FDS-MIMO)阵列结构,并对该体制的自适应波束形成进行了深入研究。不同于已有成果,本文所采用的面阵频率分集阵列全维处理面临高维度和高计算复杂度问题,为此,本文基于所建立的信号模型,理论导出了基于等效载频的权向量分解解析解,提出了一种分解迭代的稳健波束形成新算法,通过将全维加权向量估计转化为一个循环迭代的降维权向量估计问题,有效提高了波束形成算法的运算效率和鲁棒性。同时,通过子孔径阵列间采用互质频偏实现了距离栅瓣的抑制,有效降低了传统方法存在的周期性输出SINR损失问题。

2 FDS-MIMO雷达信号模型

(1)

dmn(θ,φ)=Crr′mnar=(m-1)dxcosθcosφ+

(2)

其中,目标坐标系中雷达视线归一化方向矢量ar=r/r=(cosθcosφ, cosθsinφ, sinθ)T,而转换矩阵为

(3)

从而子阵(p,q)的阵内发射流形矢量可以写成

apq(θ,φ)=[ap(θ,φ)∘aq(θ,φ)]

(4)

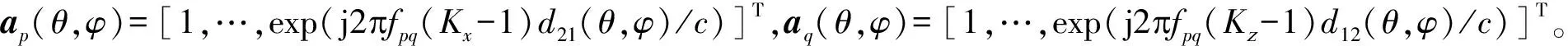
Apq(θ,φ)=

(5)

其中,fpq表示子阵(p,q)的发射载频,可以表示为

p=1,2,…,P;q=1,2,…,Q

(6)

假设子阵(p,q)发射的信号为

(7)

(8)

图1 FDS-MIMO雷达阵列结构示意图Fig.1 Basic geometry of the FDS-MIMO radar

其中,τ表示任意时延。在点目标的假设下,所有子阵发射信号和可建模如下

(9)

其中,wpq是子阵(p,q)的加权向量。假设所有的子阵波束都指向(θ,φ),则非自适应波束形成权向量可以表示为

wpq=apq(θ,φ)/‖apq(θ,φ)‖F

(10)

因此(9)可以简化为

(11)

则第(m′,n′)个天线接收到的信号可以表示为

exp(j2πfpq(t-(τ0-τm′n′)))

(12)

其中,τ0=2r/c表示参考点与目标之间的双程时延,c表示光速,α是目标的散射系数,τm′n′=dmn(θ,φ)/c表示参考点和阵元(m′,n′)之间的传播时延。利用波形φm′n′(t)exp(j2πfm′n′t)对xm′n′(t)进行正交匹配滤波[7,15],可得第(m′,n′)个阵元的第(p,q)个通道的输出为

α·exp(j2πfpq(τm′n′-τ0))Apq(θ,φ,fpq)=

α′·Bm′n′(θ,φ)Apq(θ,φ,fpq)Rpq(r)

(13)

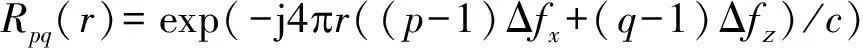
X0=α′·U(θ,φ,r)

(14)

y=α′·νec[U(θ,φ,r)]

(15)

为简洁起见,记u(θ,φ,r)=νec[U(θ,φ,r)],假设远场存在一个期望信号和J个非相干干扰,接收的回波信号为

(16)

其中,α′0和α′j分别为目标和干扰的散射系数,n是与信号和干扰不相关的噪声。

3 提出的FDS-MIMO雷达分解迭代稳健波束形成算法

3.1 基于不确定集的稳健波束形成算法

最坏情况下性能最优算法(Worst-Case)是一种常用的波束形成算法,其通过定义导向矢量的不确定集和优化最坏情况下的性能来确定最优对角加载因子[20]。文献[15]将该方法扩展到FDA-MIMO雷达,其核心思想也是假定真实的导向矢量位于一个不确定的椭圆集内,并基于最差情况下的波束输出SINR最高为准则求解导向矢量,即

(17)

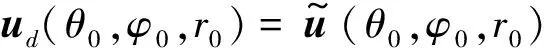
s.t.wHud(θ0,φ0,r0)≥ε‖w‖+1

Im{wHud(θ0,φ0,r0)}=0

(18)

其中,权向量w可利用内点法求解。然而,由式(16)可知,本文FDS-MIMO雷达的权向量w维数很高,利用式(18)求解必然导致全维处理的计算复杂度高和快拍数需求大等问题[21]。

3.2 FDS-MIMO雷达权向量分解

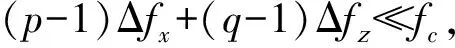
Δpq=2π(fb-fpq)τm′n′

(19)

其最大值为

(20)

更进一步,根据文献[22]的边界条件,max(Δpq)≤π/4=0.785时对系统性能的影响可忽略。

图2 三种频偏下不同阵列维数最大相位误差曲线Fig.2 The maximal phase error versus array dimension under three kinds of frequency offsets

Bm′n′(θ,φ)≈exp(j2πfb((m′-1)d21(θ,φ)+

(n′-1)d12(θ,φ))/c)

(21)

同理,可得发射阵间导向矢量的第(p,q)个元素Apq(θ,φ)可表示为

Apq(θ,φ)≈

(22)

为方便后续分析,定义辅助向量F(γ,P)=[1,exp(jγ),…,exp(j(P-1)γ)]T,从而可得

FT(2πfbKxd21(θ,φ)/c,P)

(23)

B(θ,φ)=F(2πfbd12(θ,φ)/c,N)·

FT(2πfbd21(θ,φ)/c,M)

(24)

(25)

相应地,发射流形矢量可以表示为

AR(r,θ,φ)=R(r)⊙A(θ,φ)

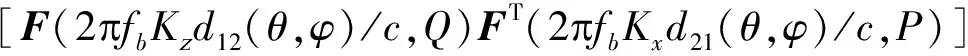
F(-4πrΔfx/c+2πfbKxd21(θ,φ)/c,P)T

(26)

其中,⊙表示Hadamard乘积。从上式可知发射流形矢量不仅是角度依赖的,同时也是距离依赖的。对其按列进行拉直操作有

ar(r,θ,φ)=

F(-4πrΔfx/c+2πfbKxd21(θ,φ)/c,P)⊗

(27)

其中,⊗表示kronecker乘积,而将B(θ,φ)按列拉直操作则有

b(θ,φ)=νec[B(θ,φ)]=F(2πfbd21(θ,φ)/c,M)⊗

F(2πfbd12(θ,φ)/c,N)

(28)

于是阵列的发射-接收联合流行矢量可以写成如下的kronecker积形式

u(θ,φ,r)=F(-4πrΔfx/c+2πfbKxd21(θ,φ)/c,P)⊗

F(2πfbd21(θ,φ)/c,M)⊗F(2πfbd12(θ,φ)/c,N)

(29)

为表示方便,记u(θ,φ,r)=ap⊗aq⊗am⊗an。根据导向矢量u(θ,φ,r)的可分解性,权向量w也可以进行分解[23-24],于是全维权向量w可以表示为4个低维权向量的kronecker积形式

w=wp⊗wq⊗wm⊗wn=

(Ip⊗wq⊗wm⊗wn)wp=

(wp⊗Ip⊗wm⊗wn)wq=

(wp⊗wq⊗Ip⊗wn)wm=

(wp⊗wq⊗wm⊗Ip)wn

(30)

将上式代入式(18)可得对应的代价函数为

s.t. (wp⊗wq⊗wm⊗wn)Hu≥

ε‖wp‖‖wq‖‖wm‖‖wn‖+1

Im{(wp⊗wq⊗wm⊗wn)Hu}=0

(31)

3.3 FDS-MIMO雷达分解迭代稳健波束形成算法

虽然优化问题(31)是一个多元二次代价函数,难以直接求解,但如果固定其中三个变量,就可以转化为二次凸优化问题,此外易知4个低维权向量之间存在尺度模糊,为了不损失输出SINR的情况下消除这一模糊,可进行归一化处理,即‖wq‖=‖wm‖=‖wn‖=1。下面基于循环迭代的思想[25]求解式(31),若假定wq,wm和wn已知且范数为1,则根据式(30)和(31)可得如下关于wp的代价函数

(32)

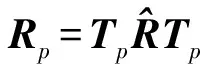
ε‖wp‖‖wq‖+1

(33)

ε‖wp‖‖wm‖+1

(34)

ε‖wp‖‖wn‖+1

(35)

1)给定初始值wq(0),wm(0)和wn(0)并进行归一化使其范数为1;

2)将wq(i-1),wm(i-1)和wn(i-1)代入式(32)求解wp(i)(i=1,2,…);

3)将wp(i),wm(i-1)和wn(i-1)代入式(33)得到wq(i);

4)将wp(i),wq(i)和wn(i-1)代入式(34)计算wm(i);

5)将wp(i),wq(i)和wm(i)代入式(35)计算wn(i);

6)其中,步骤3)～5)求得的权向量要进行范数归一化处理,重复步骤2)～5),直到max{‖wq(i)-wq(i-1)‖,‖wm(i)-wm(i-1)‖,‖wn(i)-wn(i-1)‖}≤δ(0<δ≪1)迭代结束,此时的权向量估计为w=wp(i-1)⊗wq(i-1)⊗wm(i-1)⊗wn(i-1)。

3.4 提出方法性能分析与讨论

本节从两个方面讨论所提算法的性能。

(1)样本需要量和计算复杂度:由上述分析可知本文方法分别需要估计Mi×Mi,i=P,Q,M,N的4个协方差矩阵,由此可知所提算法的训练样本只需不小于max{P,Q,M,N}。全维Worse-Case算法需要估计的协方差矩阵为C×C(C=PQMN)维,由于采用了系统的全部自由度,样本数大于等于C时才能保证内点法正常工作。用内点法求解时,Worst-Case算法的计算复杂度为O(BP3Q3M3N3),其中B为迭代次数,一般需要10次左右[20],而本文算法求解4个低维的凸优化问题的运算量为O(B(P3+Q3+M3+N3)),其分解迭代次数一般为4～5次,可以看出到本文方法的运算量O(5B(P3+Q3+M3+N3))≪O(BP3Q3M3N3),因此与Worst-Case算法相比,本文方法的计算复杂度和训练样本需求都明显降低。

(2)SINR损失分析:当干扰源离目标很近时将会导致干扰抑制性能的损失,文献[15]定义了SINR损失来衡量,其定义为

(36)

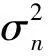
(37)

(38)

rj-r0=Px·c/(2NxΔf)

(39)

(40)

(41)

4 仿真实验与结果分析

为了验证本文所提算法的有效性,设FDS-MIMO雷达包含M×N=6×6个天线单元并划分为P×Q=3×3个子阵,倾斜角β=10°,载频fc=300 MHz,天线间距为半波长,基础频偏Δf=3 kHz,迭代停止门限δ=0.01。噪声建模为复高斯白噪声,目标位于{10°, 50°, 30 km},其散射系数服从Swerling-II模型[26]。同时,为了对比分析本文方法的性能,仿真实验添加了3种算法进行对比,分别是采样求逆算法(SMI);对角加载算法(LSMI),其加载量为噪声功率的10倍;以及文献[15]中采用的Worst-Cases算法。

仿真 1 导向矢量精确已知

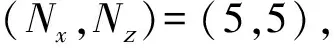
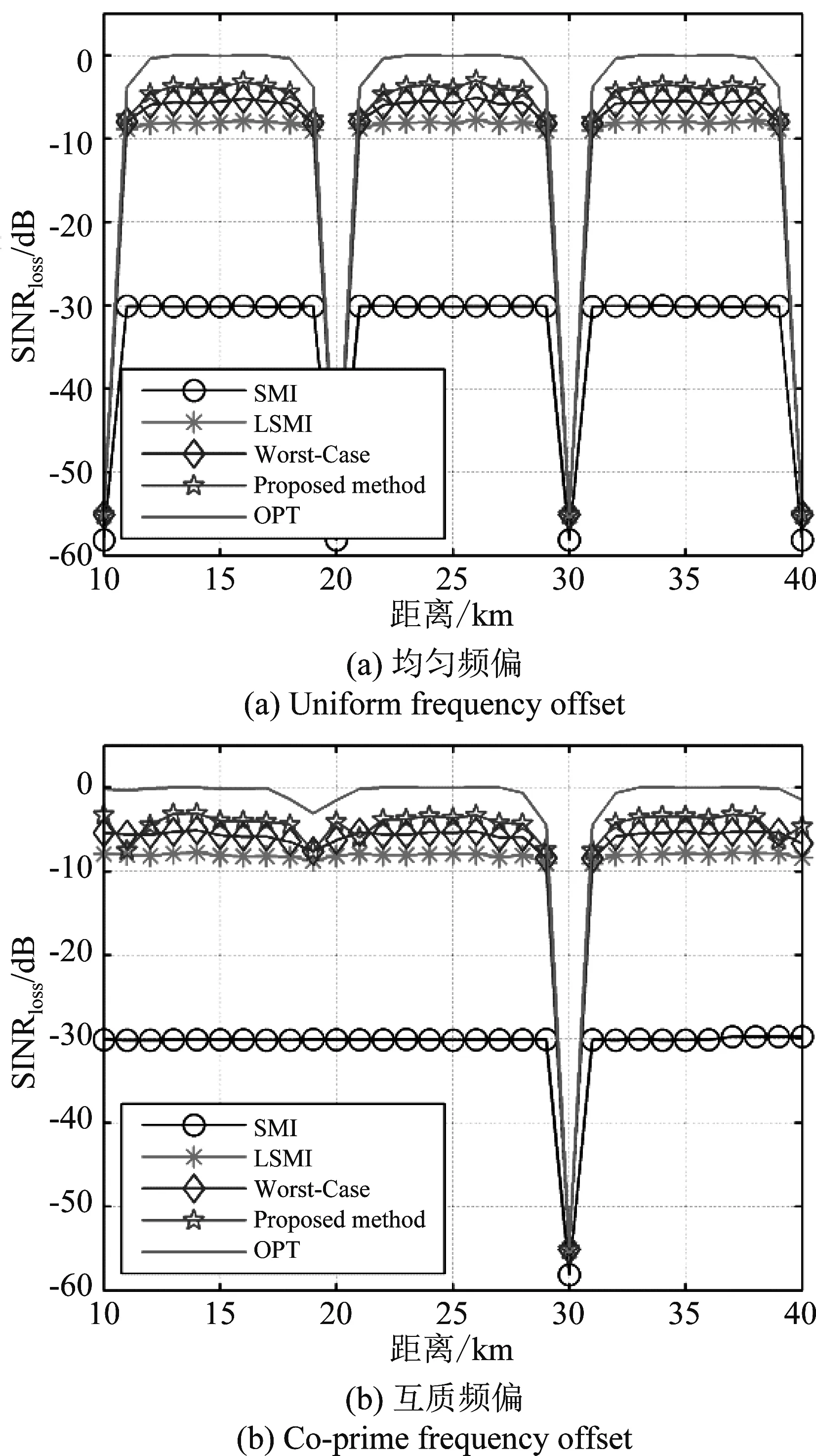
图3 SINR损失随干扰距离变化曲线Fig.3 SINR loss versus the range of interference

仿真 2 导向矢量距离角度失配

仿真 3 导向矢量随机失配

本试验在仿真2的基础上,考察导向矢量随机误差对算法性能的影响。设随机导向矢量误差服从零均值,方差为0.01的高斯分布,其他参数与仿真2一致。图5给出了导向矢量随机失配情况下各算法性能对比曲线,其中图5(a)中采用的快拍数为648,图5(b) SNR为5 dB。对比图4(a)和图5(a)可以看出在随机导向误差情况下Worst-Case算法受随机误差影响较大,性能有较大下降,而本文方法性能基本保持不变,其原因在于当导向矢量存在随机误差时,ε不再是最佳的球形不确定集值,特别是当ε小于实际的最佳值时,Worst-Case算法性能会明显下降,而本文的迭代算法能够通过迭代逐步收敛到真实的导向矢量,这也是本文算法抗随机误差更加稳健一个原因。此外,对比图4(b)和图5(b)可以看出在随机误差情况下,本文算法性能几乎不受影响,且明显优于其他3种方法,进一步证实了本文提出算法的稳健性。

图4 导向矢量距离角度失配情况下各算法性能对比Fig.4 Algorithms performance comparison under the steerig vector mismatch in range and angle

图5 导向矢量随机失配情况下各算法性能对比Fig.5 Algorithms performance comparison under the random steerig vector mismatch

5 结论

针对频分MIMO雷达稳健波束形成问题,本文建立了米波频分子孔径MIMO雷达信号模型,理论导出了其导向矢量分解的解析表达式,并进一步提出了一种分解迭代稳健自适应波束形成算法。研究表明,通过将原始的全维问题转化为低维权向量的估计问题,较大的提高了计算效率。同时,本文算法能够有效抑制距离栅瓣带来的周期性SINR损失问题,且在导向矢量失配时较之传统全维算法具有更高更稳健的输出SINR。