基于平衡稳定性的货币危机预警模型及实证研究

王振齐,龙 文

(1.中国政法大学商学院,北京102200;2.中国科学院虚拟经济与数据科学研究中心,北京100190;3.中国科学院大学经济与管理学院,北京100190;4.中国科学院大数据挖掘与知识管理重点实验室,北京100190)

1 引 言

世界范围内接连不断的金融危机逐渐暴露出金融危机的破坏性,这些问题在新兴市场及发展中国家尤为突出.因此,选择一套恰当的指标,构建一个有效的危机预警体系就显得尤为重要.从20世纪70年代开始,就有很多学者研究危机预警模型.Krugman[1]将汇率制度引入危机研究中,认为投机者对汇率的攻击将导致货币贬值,从而引发货币危机.Frankel等[2]开创了货币危机预警模型的先河,以1971年∼1992年中100个发展中国家为样本,建立了估计危机发生可能性的FR概率模型.Sachs等[3]提出STV横截面模型,克服了FR模型没有考虑国别差异的缺陷.Kaminsky等[4]建立了信号分析法KLR模型,把预测商业周期转折点的信号法用于寻找货币危机的影响因素.STV模型和KLR模型是目前国际上应用最广泛,认可度最高的预警模型.Berg等[5]利用拉美国家和东南亚金融危机国家的历史数据检验预警模型对危机的预测能力,发现KLR模型的预测效果最好,STV模型次之,FR模型最差.后来不少学者从其它角度解读货币危机的原因.Kumar等[6]基于滞后的宏观经济和金融市场数据提出Simple Logit模型,较好地解释了墨西哥货币危机,亚洲金融危机以及巴西货币危机.

由于STV模型适用性广,数据易获得,很多学者力图对其进行改进,使其与实际情况更加吻合.比如,Nitithanprapas等[7]在STV横截面回归模型中,除考虑汇率和外汇储备因素,又构造了一个反映经常账户平衡、国际资本流动的复合变量,得到稍好的预测效果.近年来,经济全球化不断增强,货币危机也更加复杂多变,很多研究从实证角度进行了分析,Alessandri等[8]、Repullo等[9]通过检验美国、英国、法国和德国等国家的GDP增长率、信贷增速、信贷占GDP的比重、资产价格、银行税前利润和信用价差等变量,发现信贷与GDP的比率仍可以作为系统性风险的有效预警指标.

在对中国的实证研究中,有一些学者较为认可KLR模型.比如,史建平等[10]利用KLR模型对新兴市场国家现阶段的金融危机做了实证检验,结果显示KLR模型的预警效果较好,认为2009年我国发生金融危机的风险较小.另一方面也有不少学者认为三大模型并不适用中国情况.比如,徐道宣等[11]在阐述KLR信号分析法时指出该分析法在中国应用时存在相关性不足等问题.马德功等[12]对比FR概率模型、STV模型、KLR信号分析模型,发现由于模型的非结构化,这些模型并不适应我国情况,并在FR模型的基础上构建起一个非线性的预警模型以克服前几个模型的不足.

考虑到上述建模情况及非线性预警模型对中国有较好的适应性,本文利用非线性的矢量分析法结合平衡稳定性理论分析货币系统风险,以“实际汇率变动率、私营部门贷款与GDP比率的变动率、总储备与M2的比率”三个指标构建“介稳球内接三棱椎”预警模型,基于平衡稳定性理论研究三棱锥的失稳特征,考察三棱锥重心在球内外的分布情况,同时观察对应的货币系统稳定性变动规律.文章进一步考察了1997年亚洲金融危机前后各国经济系统稳定性特征,进而对近年来我国货币系统稳定性情况进行研究,并结合2016年第一季度经济运行情况分析我国当前系统性风险.

2 “介稳球内接三棱椎”预警模型

首先介绍在预警危机模型中应用最为广泛的STV模型,进而选取货币危机预警的指标变量,构建“介稳球内接三棱椎”预警模型,然后用平衡稳定性理论研究三棱锥的稳定性变动特征,观察对应的货币系统稳定性变化规律,论证模型合理性.

2.1 STV模型

Sachs等[3]通过考察1994年∼1995年间的墨西哥金融危机和其后在东南亚部分新兴市场国家发生的危机过程,发现实际汇率(RER)的变动、国内信贷规模(LB)扩张和广义货币供给与外汇储备的比率(MR)对一个国家是否发生危机起着决定性的作用.

在危机指数(IND)的构建上,Sachs等[3]通过借鉴Frankel等[2]及Eichengreen等[13]的指数构建方法,利用汇率变动率和外汇储备变动百分比的加权平均值作为危机指数.

在自变量选择上,他们借鉴Frankel等[2]研究货币危机特征时提出FR的模型,发现货币贬值超过25%、经济增长迟缓时国内信贷增长过快易导致货币危机的发生,故使用实际汇率(RER)的变动作为第一个变量,选取银行对私有部门的债权与GDP的比率(LB)作为第二个变量.考虑到一国在预防货币危机方面存在消耗外汇储备或提高利率的措施,借鉴Sanz-Serna等[14]用广义货币和外汇储备的比率(MR)测量一国外汇储备丰度的方法,选取MR作为第三个变量.为对新兴市场国家进行分类,Sachs等人设计两个虚拟变量DWF和DLR.当一国的汇率、银行信贷在四分位变动,说明经济基本面比较稳定,表示为DWF=0,否则取DWF=1.同样,当一国MR在最高四分位时说明该国外汇储备充足,取DLR=0,否则取DLR=1.回归模型为

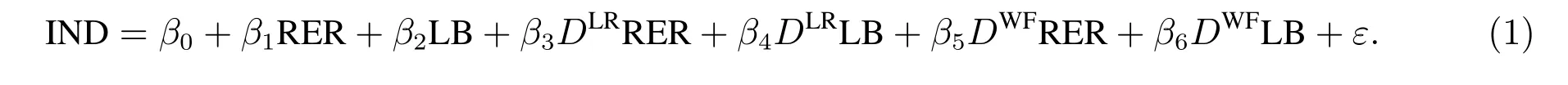
Sachs等[3]的实证研究表明STV模型较好地揭示了新兴市场国家发生金融危机的原因.此后STV模型得到了广泛的应用和发展.

2.2 危机预警指标的选取

STV模型提出以后,为进一步验证其它学者有关投资、储蓄、政府消费、经常账户和资本流动等指标影响货币系统稳定性的观点,Sachs等人补充这些指标及其变动率作为自变量,以测定其对金融危机的影响,但实证表明这些变量或者统计意义不显著,或者影响不大.鉴于此,本文仍旧选取STV模型的三个指标:实际汇率(RER)的变动、私营部门贷款与GDP比率(LB)的变动、广义货币与外汇储备的比率(MR)作为影响货币系统稳定的基本要素.

对于实际汇率(RER)的变动,选择稳定发展阶段的年份为基期,计算后期各年度的相对变化率,计算公式为 Ri=(εi− ε0)/ε0.

鉴于STV模型中私营部门贷款与GDP比率(LB)在万分位及以下变动时,一国经济基本面比较稳定,而LB在千分位、百分位变动时基本面较差.因此取Li=−(LBi−LB0)/LB0.

考虑到广义货币与外汇储备的比率(MR)往往是远大于1的,而本文所构建的模型要在直径为1的球里面进行矢量运算,所以对MR取倒数变换,即Mi=1/MRi.

下面将先根据经济指标的等间隔采集特性构建“介稳球内接三棱椎”预警模型,再利用平衡稳定性理论分析三个指标变动对系统稳定性的影响.

2.3 介稳球内接三棱椎预警模型的构建

图1描绘了点出发的时间序列.

图1 点出发的时间序列Fig.1 Time series starting from a point

如图1所示,张昴等[15]在研究非线性时间序列时,结合经典力学的矢量分析法,提出了点发出的时间序列模型.将时间跨度相同的样本数据Ri以其大小从圆的最低点出发沿着−−→ORi方向刻画在圆里面,进而根据矢量的合成及分解法则对指标做非线性分析及运算.

本文选取的三个经济指标Ri,Li和Mi都是年度数据,具备构建点出发的时间序列的条件.一方面单个指标时间序列各期之间是等时间采集的,即单个经济指标是纵向等时的;另一方面三个指标的截面数据都是上年末开始到本年末结束为周期算的,即三个数据指标是横向等时的.因此,可以将三个指标序列表示在等时球里.

如图2所示,在空间直角坐标系中,鉴于指标都是(−1,1)区间的数据,为方便下面的计算,画出以H(0,0,0.5)为球心,以1为直径的球,记最高点为O′.选取球面与XOZ平面正方向相交所得圆弧ORO′为实际有效汇率变动率Ri序列所在圆.考虑到对称性,选取半圆弧OLO′,OMO′与ORO′两两夹角均为120°.基于此将各期指标Ri,Li和Mi以其大小从最低点出发沿着弦的方向画到对应的圆里,画出三条弦.注意指标可以为负值,因此对球做关于水平面XOY的镜像,把负值数据画到下方对应的圆弧上,得到三棱椎O-RLM,其重心为G.

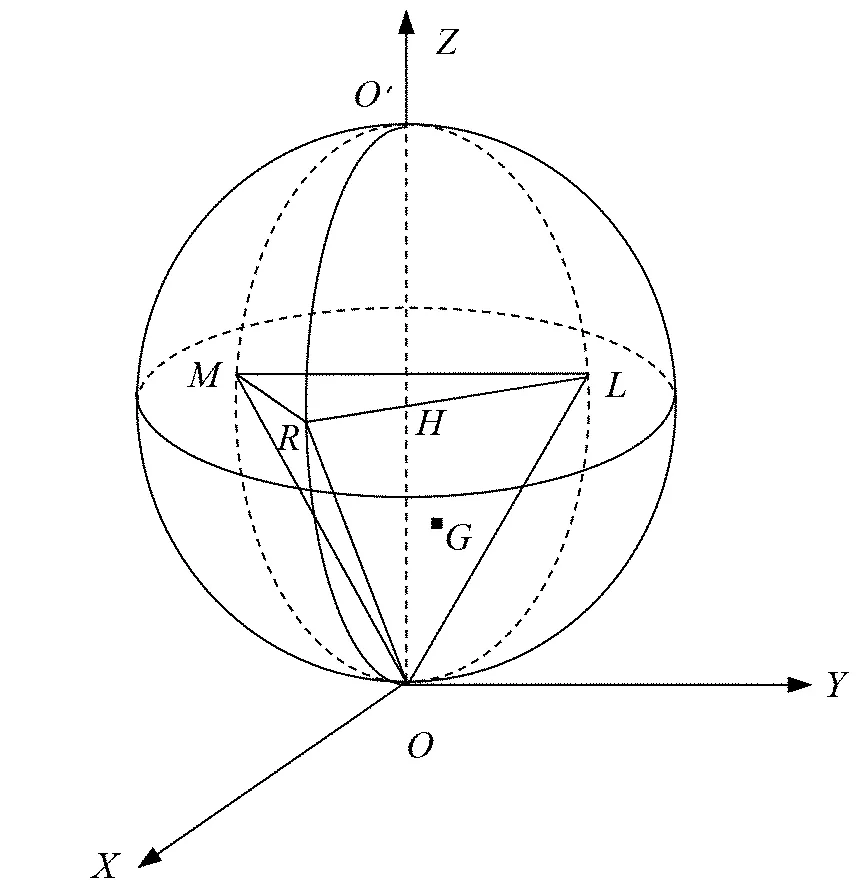
图2 等时球内接三棱锥Fig.2 Triangular pyramid in the isochronous ball

刘骏民等[16]认为介稳性是指经济持续增长过程中的均衡性质,某些部门虚假繁荣导致均衡的增长被打破,危机过后回归均衡.经济系统在稳定性遭受破坏后,可能在一定的范围内游动,交替地进入平衡和非稳定平衡态[17].汪寿阳等[18]指出可以将金融经济体系看作是一类复杂性系统,从系统内部的结构及外部作用来考察系统的特性,以揭示金融经济体系演化的规律.结合以上观点,本文将图2所示的三棱锥命名为“介稳球内接三棱锥”,以刻画货币系统的稳定性.

2.4 货币系统稳定性与三棱锥重心波动的联系

为直观显示抽象的数学物理系统稳定性和简化的货币系统稳定性的一致变动规律,本文借鉴徐元栋[19]、李勇建等[20]通过数值仿真模拟动力学模型及相关变量,以显示系统发展演化规律的思想,在控制变量的前提下通过单变量的变动来分析重心G的移动规律,进行随机数模拟实验.

1)实际有效汇率贬值时,根据 Ri=(εi−ε0)/ε0,则缩小,知随之缩小,G点距离O点更近,此时重心趋向内接球外,即逐渐变大,直到大于球的半径时,三棱锥重心G落在球外.Kaminsky等[4]指出实际有效汇率贬值是1997年各国发生金融危机的重要原因和直接体现.本文在控制变量的前提下进行随机数模拟,样本量为30,观察单变量与重心预警距离的变动情况,结果如图3所示.随机产生的汇率变动率序列与其对应的重心预警距离序列呈现反向变动关系,即汇率贬值时,重心预警数值变大,容易发生危机,此时重心趋向球外;汇率升值时,重心预警数值变小,此时重心趋向球内.

2)私营部门信贷增长过快时,GDP增长率减缓时,根据Li=−(LBi−LB0)/LB0,则=Li缩小,知随之缩小,G点距离O点更近,此时重心趋向内接球外.Frankel等[2]在研究近代以来的货币危机时,指出经济增长迟缓时,国内信贷增长过快易导致货币危机的发生.在控制变量的前提下进行随机数模拟,样本量为30,观察单变量与重心预警距离的变动情况,结果如图4所示.随机产生的贷款变动率序列与其对应的重心预警距离序列也呈现反向变动关系,效果同汇率变动率.

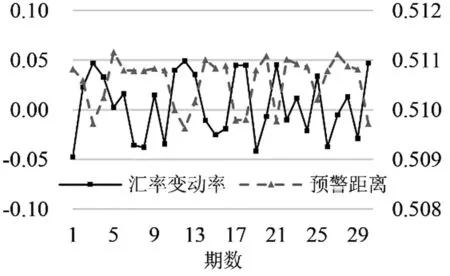
图3 随机数模拟汇率变动率与预警距离的变动情况Fig.3 Stochastic simulation of the change in the exchange rate and the warning distance

图4 随机数模拟贷款变动率与预警距离的变动情况Fig.4 Stochastic simulation of the change in loansand the warning distance

3)总储备规模降低时,M2增速过高时,根据Mi=1/MRi,则缩小,知随之缩小,G点距离O点更近,此时重心趋向内接球外.Sanz-Serna等[14]在研究1994年墨西哥金融危机时指出外汇储备较小时,金融系统就很难应对外来冲击.Kaminsky等[4]在研究1997亚洲金融危机时也发现该变量显著.在控制变量的前提下进行随机数模拟,样本量为30,观察单变量与重心预警距离的变动情况,结果如图5所示.随机产生的储备比序列与其对应的重心预警距离序列也呈现反向变动关系,效果同汇率变动率.

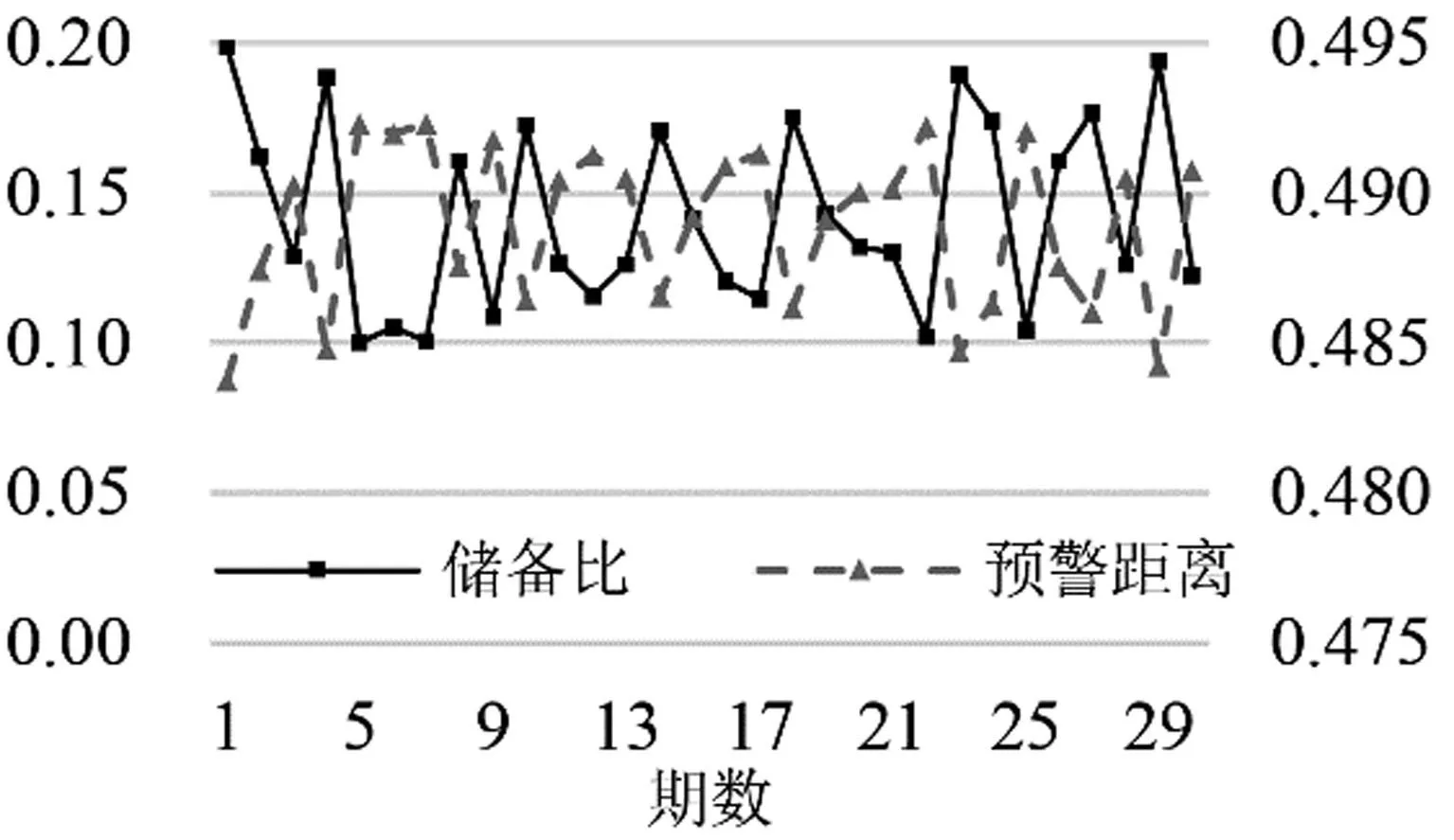
图5 随机数模拟储备比与预警距离的变动情况Fig.5 Stochastic simulation of the reserve ratio and the warning distance

以上各种不利变动都使得重心向球外运动,三棱锥趋向失稳,对应到货币系统中,系统就表现为不稳定,而历史上各国危机前后的变动也很好地吻合这个变动特点.据此,可构建出“介稳球内接三棱椎”预警模型,根据模型的预警距离便可对货币系统的稳定性进行判断.

2.5 预警距离的数值计算

如图2所示,先表示出三棱锥O-RLM顶点坐标,然后根据重心公式计算出三棱锥的重心G,进一步用空间距离公式便可求出重心G与球心H的距离

对于实际有效汇率变动率序列R中样本点对应半圆弧中弦设其仰角(与水平面的夹角)为θ,根据弦切角定理和圆周角定理,在直角中,弦长为sinθ,即有θ=arcsinr.进而在空间直角坐标中得R点坐标(sinθcosθ,0,±sinθsinθ).其中正负符号表示R点的Z轴坐标可正可负,同理可得L点,M点坐标.根据重心公式=0,即有重心G坐标进一步可得预警距离为

2.6 介稳球内接三棱椎预警的优势

与传统方法相比,本文所构建的“介稳球内接三棱椎”预警模型具有以下优势:

1)用矢量刻画系统的非线性.STV模型的一个众所周知的局限性是该模型是线性的,但是在实际中,各指标之间的关系却是非线性的,所以STV模型未能准确地表达出实际指标之间的相互作用关系.本文提出的“介稳球内接三棱椎”预警模型根据矢量的合成及分解法则对指标做非线性分析及运算.

2)客观定义预警距离.Sachs等[3]借鉴Frankel等[2]、Kaminsky等[4]、Eichengreen等[13]的指数构建方法,将汇率变动率与和外汇储备变动百分比的加权值定义为危机指数.但是仅仅使用这两个数据构建指标未免有失偏颇.比如说,因为数据的局限未能考虑到利率对危机指数的影响作用,进而丢失了很多有价值的信急.本文避开了人为主观定义危机指数的局限性,从一种较为客观的方式出发,利用平衡稳定性理论对系统是否平衡态做出判断,通过考察三棱锥重心在球内外的分布情况,观察同步变动的货币系统平衡特征.

3 对1997年亚洲危机的研究及模型对比

Berg等[5]利用拉美国家和东南亚金融危机国家的历史数据检验危机预警模型对危机的预测能力,发现KLR模型的预测效果最好,STV模型次之,FR模型最差.本文在此基础上,加入“介稳球内接三棱椎”预警模型对1997年的金融危机再次进行实证研究,以进行比较.

3.1 亚洲危机前后各国系统稳定性情况

由于金融危机始发于1997–07,持续到1999年末结束,相对来说1994年是各国较为稳定的时期,1993年、1994年间各国货币政策、汇率、贸易政策等均未发生大的改变,各国政治局面比较稳定,因此以此为基期是合适的.按照第2节提出的预警距离计算方法,求得1997年亚洲金融危机前后各国系统稳定性情况,如图6所示.

图6 1997年亚洲金融危机前后各国系统稳定性情况1数据来源:“实际有效汇率指数”来源于国际清算银行;“私营部门的国内信贷与GDP的比率”来源于世界银行;“货币和准货币(M2)与总储备的比率”来源于国际货币基金组织.图中结果根据以上数据计算得出.Fig.6 System stability among countries before and after the 1997 Asian financial crisis

图6是根据计算出的预警距离所显示的亚洲货币危机前后各国货币系统稳定性情况,本文将在3.2小节做整体分析,然后针对1997年危机时各国稳定性这个关键性数据,按照国际货币基金组织Berg等[5]在对系统性风险度量和预警模型评价中采取的方法,在3.3节进行比较分析.

3.2 对各国系统稳定性变动的分析

如图6所示,整体上来看,各国重心分布呈现出“稳定–偏离–回稳”的周期律.重心预警距离突破0.5是受灾较为严重国家的主要特点,降到0.5以下标志着走出危机,而0.5正是“介稳性等时球”的半径,三棱椎的重心与球心距离大于0.5表示重心落在球外,即失稳的临界条件,此时的货币系统发生危机,从实证角度验证了货币系统稳定性与三棱锥重心波动的对应关系.

同时注意到乌拉圭、秘鲁和智利三国没有在金融危机后回稳,表明各国仍存在着较高的系统性风险,受危机影响,国内仍然经济不景气.表1是三个国家危机前后的GDP实际增长率,可以看到直到2002年各国仍未恢复到危机前的增长水平.

表1 危机前后三个国家的实际GDP增长率(%)Table 1 Real GDP percent growth in the three countries before and after the crisis

3.3 模型比较与评价

为度量1997年危机时各国稳定性这个关键性数据,同时对模型优劣进行比较,参照Berg等[5]关于三大危机预警模型优势比较的方法,将各种模型以及本文提出的“介稳球内接三棱椎”预警模型预测的各国危机指数进行排序,序数越小,代表发生危机的可能性越高.进而求出实际值和预测值的等级相关系数,进行预测优良性比较,结果如表2所示.

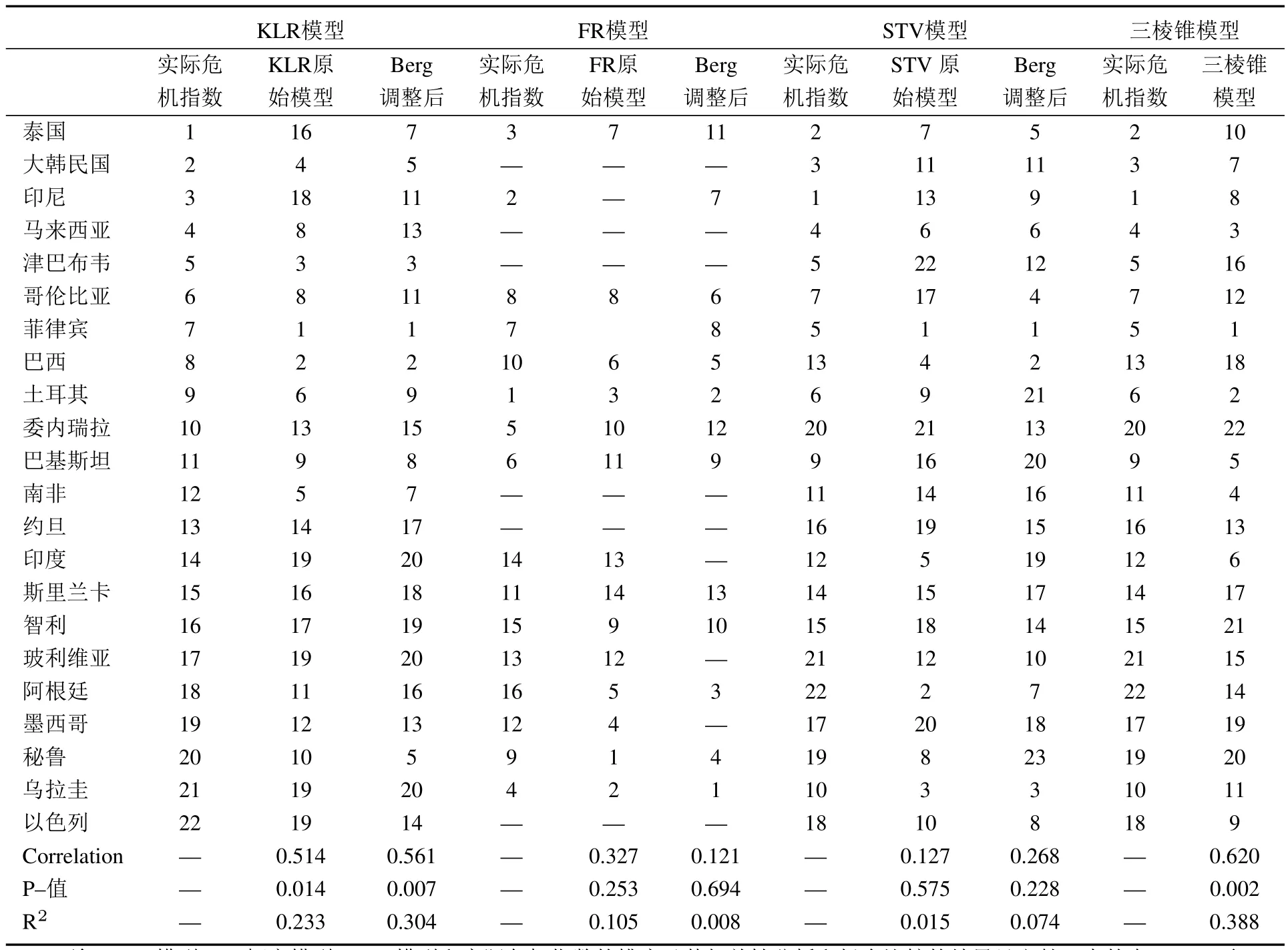
表2 各模型对1997年的预测与实际危机指数的比较Table 2 The comparison of the forecast and real crisis index for each model for the 1997 financial crisis

由表2可以看到,与传统三大模型相比,本文提出的“介稳球内接三棱椎”预警模型对货币危机的预测效果更好.从实际危机指数与模型预测指数的Spearman等级相关系数可知,本文的模型要好于传统的三大模型,且P–值显著.另一方面,将实际危机指数与预测指数作回归,拟合度R2为0.388,也远高于其它模型,显示了本文提出的“介稳球内接三棱椎”预警模型的优势.

4 现阶段我国货币系统风险的实证研究

本节将应用“介稳球内接三棱椎”预警模型考察近年来我国货币系统稳定性情况,再结合2016年第一季度经济运行情况及政府工作报告提出的2016年GDP和M2目标,分析当前我国货币系统性风险特征.

考虑到我国在2009年基本走出2008年金融危机的负面影响,本文以2009年为基期,计算各年度系统预警距离,然后对2016年我国货币系统风险进行考察,进而在风险整体可控格局下给出实际有效汇率、私营部门贷款规模、M2的变动区间.

4.1 近年来我国货币系统风险情况

按照“介稳球内接三棱椎”模型计算办法,得出各年度预警距离情况,如表3所示.

表3 2009年以来我国货币系统的重心预警距离Table 3 The warning distance of the center of gravity of China’s monetary system from 2009

从整体上来看,走出2008年金融危机以来,我国经济系统处于较为稳定的状态.与2011年、2013年相比,2012年重心预警距离有小波动,这是2012年两次降急引起私营部门贷款扩张造成的.2015年重心预警距离高于往年,这是2015年M2发行量增速(13.3%)、私营部门贷款增速(14.2%)与往年相比过高引起的.

4.2 2016年我国货币系统风险

2016–03–05,李克强总理在政府工作报告中提出2016年GDP增长率预期6.5% ∼7.0%,M2预期增长13.0%.根据国家统计局发布2016年第一季度国民经济和社会发展统计报告,2016年第一季度GDP同比增长6.7%,也说明政府规划目标相对合理.同时注意到2016年GDP增长率相比2015年有所下调,M2增幅有所提高,可能会造成系统稳定性下降.为防控货币系统性风险要合理调控实际有效汇率、私营部门贷款以及M2增发量.

4.3 2016年实际有效汇率合理变动区间

结合以上情况,对2016年指标数据做出如下假定:在一定范围内实际有效汇率在利率平价条件的作用下随利率变动.用试探法给出人民币浮动的下限,如表4所示.

表4 试探法下人民币实际有效汇率变动区间Table 4 The change interval of RMB real effective exchange rate with heuristics

2015–12美联储宣布将联邦基金利率上调25个基点到0.25%∼0.5%的水平,2016年美联储存在加急的可能性.在这个背景下人民币对美元贬值压力不断增大,几个月来人民币对美元大幅下跌.人民币实际有效汇率受到一定冲击,按照“介稳球内接三棱椎”预警模型计算,人民币实际有效汇率仍有下调空间,应该控制在124.14以上.李克强总理也多次表示,人民币没有长期贬值的基础,仍有一定的浮动区间,中国现阶段经济虽有波动,但是风险整体可控.这和文章的结论是一致的.

4.4 2016年私营部门贷款合理变动区间

2016年政府工作报告提出本年度要降低融资成本,加强对实体经济特别是小微企业、“三农”等支持,势必会带动私营部门贷款规模的稳步提升.根据国家统计局最近发布的私营部门贷款数据,2015年增长率为14.2%,依次变动0.5个百分点,对应的系统重心预警距离情况如表5所示.在维持前几年系统状态的前提下,本年度私营部门贷款增速应该控制在13.7%左右.

表5 试探法下私营部门贷款规模变动区间Table 5 The change interval of the private sector loans with heuristics

4.5 2016年M2增速合理变动区间

2015–12我国M2存量为1 392 278亿元人民币,2016年政府工作报告提出的广义货币M2增速为13%.2016–04总储备约214 186亿元人民币,计算出2016年货币系统的预警距离为0.488 19,相对于2015年以前年份来说,风险明显增强,因此建议适当下调M2增速.表6给出了M2增速变动的理论区间.同时注意到2016–05 M2增速已经降至11.8%,但是还不够.如果要把风险控制到与前几年相当的水平,使其预警距离相似,建议将M2增速控制在11.5%以下水平.

表6 试探法下M2增速变动区间Table 6 The change interval of M2 growth rate with heuristics

5 结束语

本文选取实际汇率变动率、私营部门贷款与GDP比率的变动率、总储备规模与M2的比率三个指标构建“介稳球内接三棱椎”货币危机预警模型.用平衡稳定性理论刻画三棱锥的稳定性变动特征,据此来观察对应的货币系统稳定性变化规律,论证了模型的合理性.基于该模型,文章考察了1997年亚洲金融危机前后各国经济系统稳定性特征,各国整体上呈现出“稳定–偏离–回稳”这样一个周期律,即危机前重心落在球内,危机时趋向球外,危机后回归球内.对比FR模型、STV模型、KLR模型的预测结果,发现“介稳球内接三棱椎”货币危机预警模型和实际情况更加相符,而且统计特性明显优于三大模型.进一步考察2009年走出金融危机以来我国货币系统风险情况,认为我国经济系统处于相对稳定的状态,再结合2016年第一季度经济运行情况及政府工作报告提出的GDP、M2目标分析我国当前系统性风险特征,发现2016年系统稳定性有所下降,但整体风险可控,远未达到0.5的货币危机阈值.国际上关于我国经济硬着陆的言论言过其实.另一方面也看到,和前几年相比,2016年货币系统的预警增强.如果要保持和前几年相当的稳定性,实际有效汇率应该保持在124.14以上水平;私营部门贷款增速应该控制在13.7%左右;在考察M2增速时,本文认为政府工作报告中13.0%的增速偏高,并提出2016年应控制M2增速在11.5%以下的建议.