基于非光滑方程组的智能电网实时定价
王宏杰,高 岩
(上海理工大学管理学院,上海200093)
1 引 言
随着科技的高速发展和生活水平的不断提高,人们对电力的需求有了更高的要求.电力用户希望电网是可靠的,安全的,经济的,高效的.用户希望可以实时了解供电能力,电能质量,电价状况和停电信急,根据相关信急合理安排电器使用,避峰填谷;电力企业希望可以及时获取用户的详细用电信急,合理安排生产,并为用户提供更多的增值服务.现有的电网虽然已经开始实施分段电价,但是现有的电价定价机制是基于较长时间段上的价格变化,例如按白天和夜晚,冬季与夏季划分时间段,每个时段制定不同的电价.这种实时定价研究已有较长的历史并取得了一系列的研究成果,但是显然这种定价机制不能完全满足用户和电力企业对电网的多样化需求.所以近年来具有现代先进的传感测量技术,通讯技术,信急技术,计算机技术和控制技术的智能电网引起了各国的高度关注和研究.美国,欧洲等发达国家目前都在发展智能电力系统,并且在智能电网领域取得了显著的发展.相对于美国和欧洲,我国在智能电网的研究刚刚起步,研究还集中在智能电网定价机制和理念的研究上.所以智能电网短时段实时定价问题的研究对促进智能电网的发展至关重要[1−4].
目前在智能电网实时定价问题上主要从两方面进行研究:一方面是从电力生产公司,电力销售商等角度考虑的商业定价机制.例如,文献[5,6]从供应商和需求侧管理方面利用博弈的方法建立和研究实时定价问题,通过动态和静态的博弈使价格趋于更合理.这类优化模型求解通常采用求均衡解的方法;另一方面是从公共产品角度考虑,追求社会效益的定价机制,根据社会效益最大化为目标建立优化模型,在总电量不超过发电能力前提下最大化用户收益和最小化电力供应商成本.文献[7–11]采用了社会效益模型,分别通过对偶法,乘子法和分布式算法来解决优化模型.利用乘子法,对偶法和分布式算法解决乘子问题,往往需要求解一系列无约束最小化问题,计算量大,数值不稳定,而且在算法中更多的注重资源的优化配置,电价被作为了资源配置的附属问题.本文从社会效益定价机制方面出发,利用互补理论将社会效益模型转化为带有影子价格的非光滑方程组,通过求解非光滑方程组来确定短时段的实时电价.该方法可以避免数值不稳定,计算复杂等问题,并且电价作为重要变量被求出.
2 智能电网的社会效益模型
在电力市场中,不同用户消费的电能也不同,即使消耗等价等量的电能也可能会拥有不同的满意程度.在本文中,采用效用函数来反映消费者的电量消费能力和这种偏好,即效用函数表达了用户对电能消费水平的满意度.关于效用函数,假定消费者满意度随着使用电量的增加而增加直至达到饱和消费的最大满意度,并且满意度不会出现负满意的情况(即效用函数小于零的情况).根据社会效益模型[9,10],定义电力用户的效用函数和社会效益函数.其中效用函数为
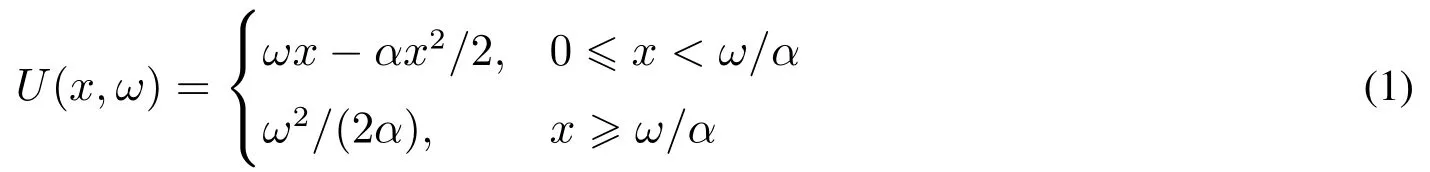
是一个二次函数,x代表电力用户的电力消费水平,它随用户与时间的不同而不同;α和ω是根据用户在每个用电时段对用电量的不同要求和满意情况选取的两个非负参数.α是预先给定的,并且满足0<α≤1的常数;ω是随着用户和用电时段而改变的非负数,如图1.

图1 用户效用函数(α=0.5)Fig.1 The utility function for powers subscribers(α=0.5)
假设共有N个电力用户和1个电力供应商,每个用电周期分为K个时段.社会效益函数为
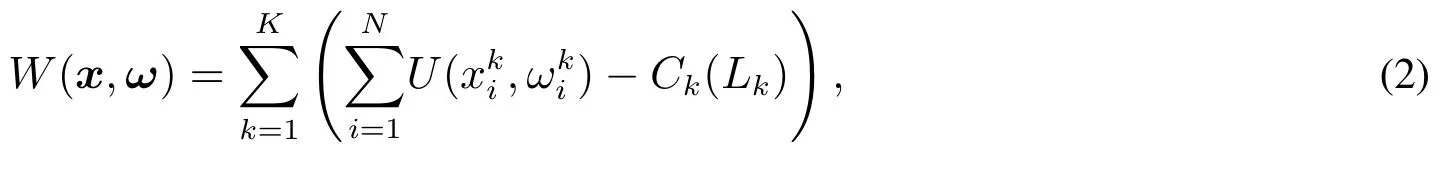
在电力系统中成本函数一般采用分段线性函数或二次函数表示[5−10],根据电力系统成本的常用计算方式,采用二次函数来表示成本,即

根据社会效益最大化,建立优化模型如下
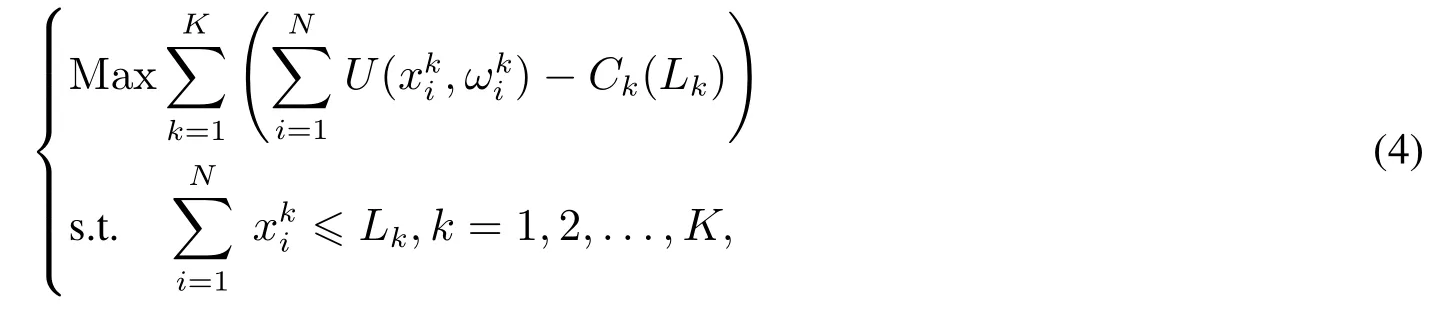
因为实际生活中,在没有突发事件的情况下用户的实际消费水平往往小于该时段其最大需求量,所以在模型中只考虑实际生产能力不超过该时段最大生产能力的情况.根据模型(4)可以通过在K个时段里分别求社会效益最大来解决,所以模型(4)可以转化为下面K个子优化问题,即
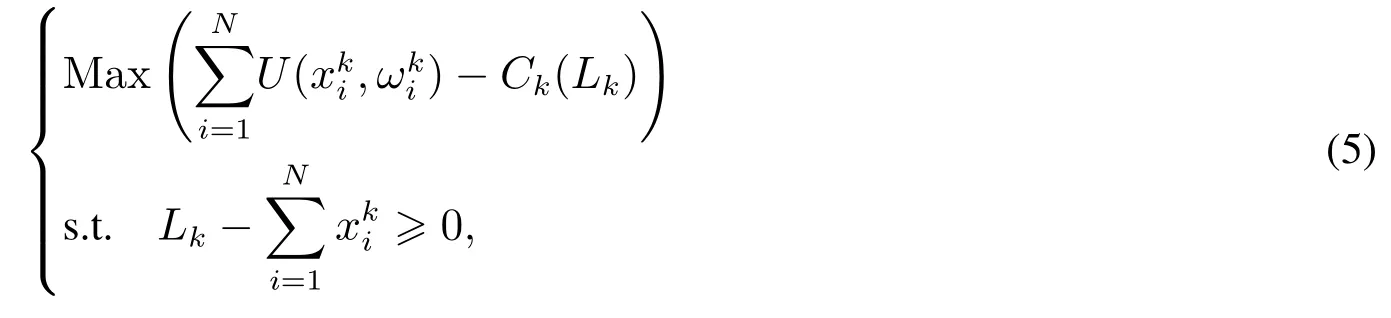
根据式(1)和式(3)的定义,可知式(5)是一个二次规划问题.根据极值定理可以知道,对于二次规划问题

其中f(x)为二次函数,g(x)=(g1(x),g2(x),...,gm(x))T,gi(x)为N元函数,x∈RN.
若x为问题(6)的一个最优解,则存在λ∈Rm使得x和λ满足下列KKT条件
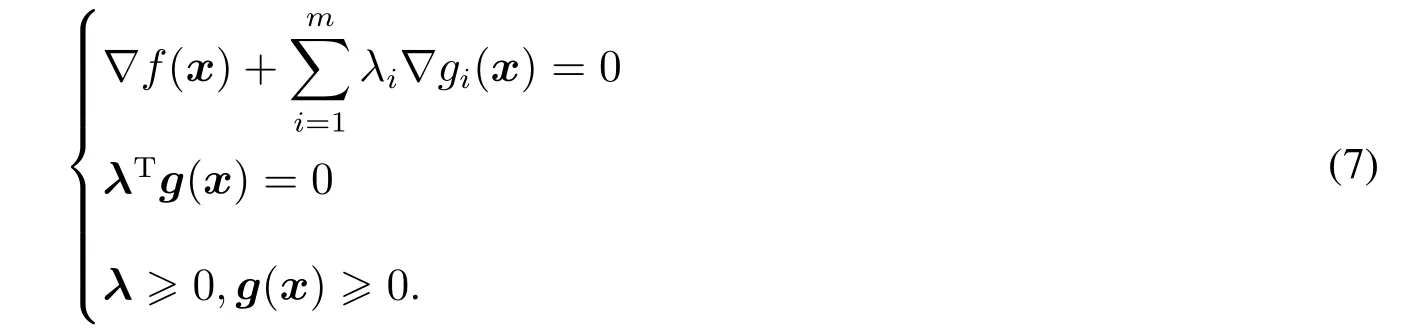
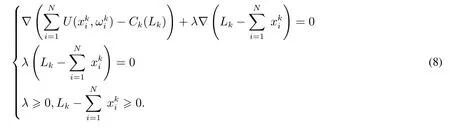
式(8)与式(5)等价,并且式(8)中的λ按经济学上的解释为电力资源的影子价格,所以可以通过式(8)来确定智能电网短时段的基础电价λ.
3 算法构造
近年来,互补问题的研究得到了极大的重视和发展,并且在力学、交通及经济等许多领域得到广泛应用.形如
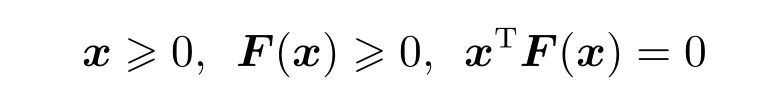
的问题被称为互补问题,其中x∈Rn,F:Rn→Rn.显然,式(8)是一个互补问题.取x和F(x)的第i个分量xi和Fi(x),为了书写方便,记第xi=a,Fi(x)=b.根据非线性互补理论[12,13]有
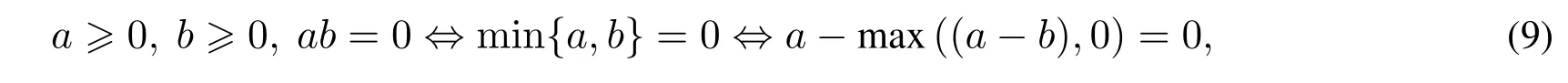
所以式(8)等价于方程组
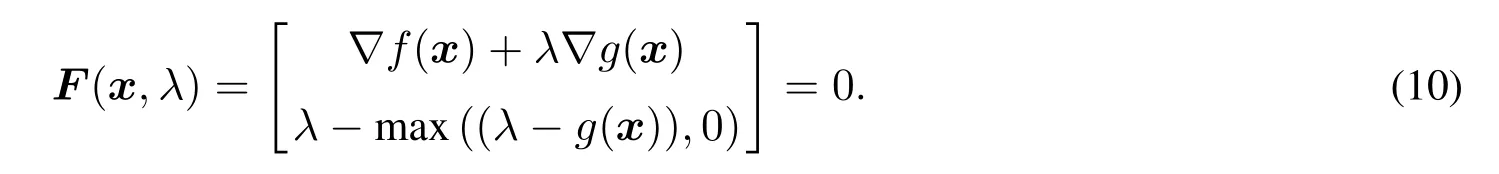
由于函数ψ(a,b)=a−max((a−b),0)在a=b处是非光滑的,因而式(10)是一个非光滑方程组,无法使用传统的牛顿法求解.目前解决这类问题常用的方法是非光滑牛顿法和光滑化牛顿法.非光滑牛顿法是利用广义牛顿类型即利用Jacobi矩阵求解;光滑化牛顿法是通过构造具有良好收敛性质的光滑函数来逼近非光滑函数求解.通过以往的研究和数值验证,研究者们发现光滑化牛顿法具有良好的收敛性,并且在数值上比非光滑牛顿法更稳定和有效.因此本文采用光滑化牛顿法来求解问题(10).
首先介绍光滑化基本思想,假设一个非光滑方程组
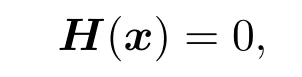
其中H(·):Rn→Rn是一个非光滑函数.再假设有一序列光滑函数Hµk(·):Rn→Rn,且满足

光滑化方法是希望通过求解光滑方程组Hµk(x)=0的解来逼近原方程组的解.
目前,构造光滑逼近函数常用方法有二次函数法,密度法,极大熵法等[12,13].为了保证解的逼近,光滑逼近函数应该满足如下定义
定义1(光滑逼近函数)[12]给定函数H(·):Rn→ Rn,称光滑函数Hµ(·):Rn→ Rn,µ > 0为H(·)的一致光滑逼近函数,如果对任意x∈Rn,存在κ>0,使得‖Hµ(x)−H(x)‖≤κµ,∀µ>0.
根据定义1和构造光滑函数的二次函数法,首先构造一个二次函数


下面证明函数ψµ(a,b)为ψ(a,b)的光滑逼近函数.
定理1函数ψµ(a,b)为函数ψ(a,b)的一个光滑逼近函数.
证明根据ψ(a,b)=a−max((a−b),0),可以得到
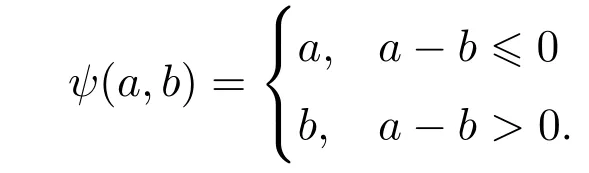
因为当−µ≤a−b<0时,有

当µ≥a−b≥0时,有
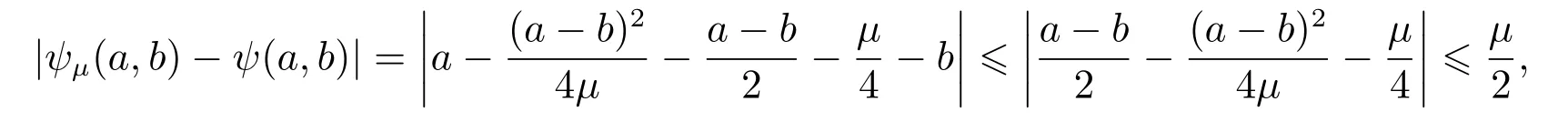
当µ<a−b或−µ>a−b时,有|ψµ(a,b)−ψ(a,b)|=0.
综上所述,当取κ≥ 1/2时,对∀µ>0,有|ψµ(a,b)−ψ(a,b)|≤κµ成立.根据定义1,函数ψµ(a,b)为ψ(a,b)的一致光滑逼近函数. 证毕.
函数ψµ(a,b)在区间[−µ,µ]内的逼近情况如图2所示.
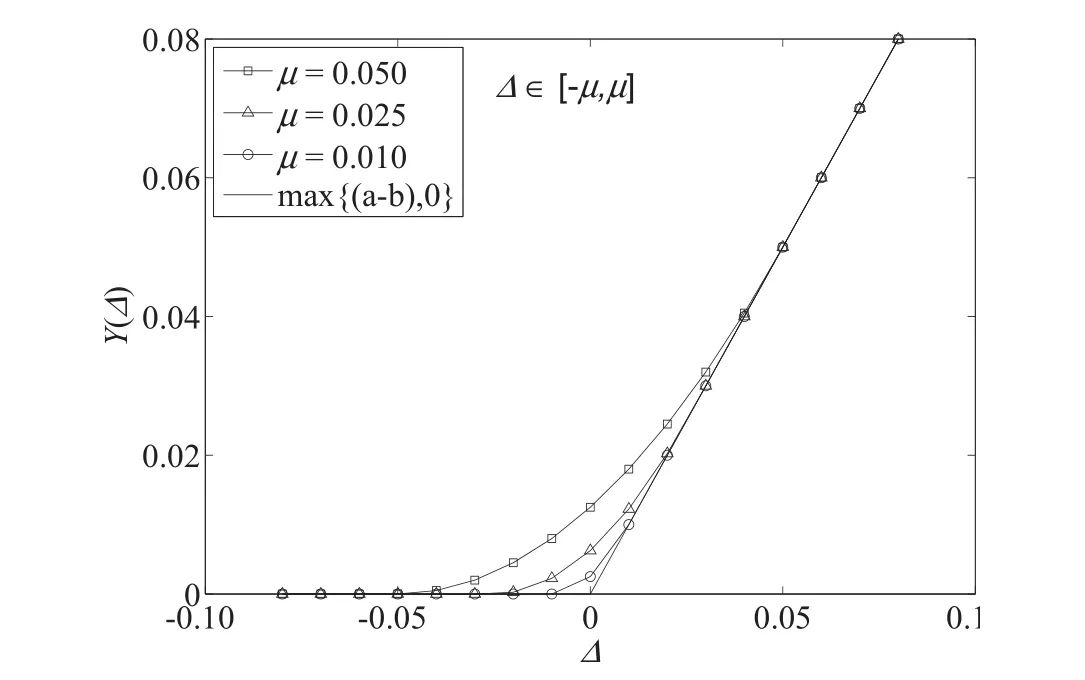
图2 非光滑函数ψ(a,b)与光滑逼近函数ψµ(a,b),在点a=b处的逼近情况,∆=a−bFig.2 The approximation of nonsmooth function and smooth function at point a=b,∆ =a−b
根据定理1,可知光滑函数ψµ(a,b)具有良好的收敛性并且随着参数µ减小逐渐逼近ψ(a,b),满足光滑化方法对光滑函数的要求.因此根据ψµ(a,b)和式(10)中F(x,λ)的构造方法,定义光滑逼近函数Fµ可以得到光滑方程组
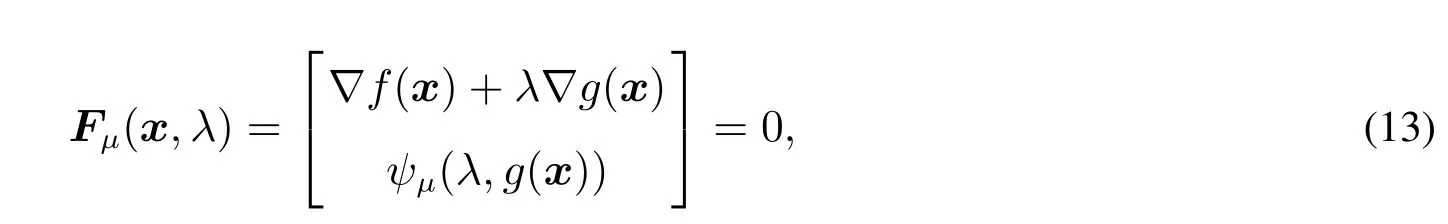
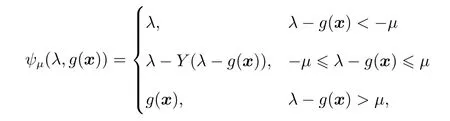
而式(13)即为要求解的问题.为了书写方便将变量x和λ记为变量X=(xT,λ)T.
因为利用拟牛顿法解方程组(13),可以避免Hesse矩阵退化的情况,而且还可以同时求出变量和电价λ,所以本文选用拟牛顿法求解方程组(13).根据拟牛顿法的PEF修正迭代公式[12,13]有

因为用户使用电量不能是负值,为了确保λ是在变量x≥0时的影子价格,解方程组(13)时,只取x≥0时的解.
算法步骤如下:
步骤1取初始点X0≥0,其中参数λ0∈(0,100),取参数Lk,选取足够小正数ε.令k=0,H0=In,µ=0.05;
步骤2判断‖Fµ(Xk)‖<ε是否成立,若成立则停止迭代,Xk即为所求;否则转步骤3;
步骤3令dk=−HkFµ(Xk),解优化问题Min‖Fµ(Xk+δdk)‖得到最优解δk.Xk+1←Xk+δkdk,转步骤4;
步骤4令Pk=Xk+1−Xk,Qk=Fµ(Xk+1)−Fµ(Xk),▽HkHk+▽Hk,k←k+1,转步骤2.
4 仿真模拟
取ak=0.01,bk=0,ck=0,α=0.5,ω∈[1,4],µ=0.05,N=6.以24 h为一个用电周期,那么在用电周期中,总电量的使用情况是由低到高再到低,在仿真中Lk的取值符合这样的形态.通过仿真模拟,得到了每个时段的实时电价λ以及电量的最优分配.同时,将新方法与固定电价方法进行了比较.其中固定电价方法的定价公式[10]为λk=ωmax−Lkα/N.结果如表1∼表4及图3∼图6.

表1 基于非光滑方程组方法和固定电价方法的电价(1)Table 1 The electricity price based on non-smooth equations method and traditional fixed price method(1)

表2 基于非光滑方程组方法和固定电价方法的电价(2)Table 2 The electricity price based on non-smooth equations method and traditional fixed price method(2)

表3 基于非光滑方程组方法和固定电价方法的社会效益(1)Table 3 The social benefit based on non-smooth equations method and traditional fixed price method(1)

表4 基于非光滑方程组方法和固定电价方法的社会效益(2)Table 4 The social benefit based on non-smooth equations method and traditional fixed price method(2)
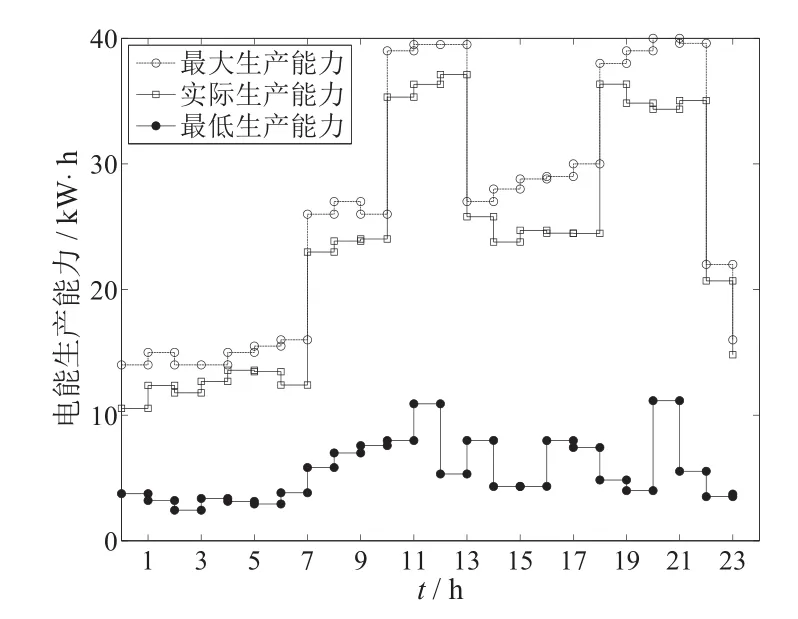
图3 基于非光滑方程组方法的智能电网生产能力Fig.3 The power Capacity of smart grid based on non-smooth equations method
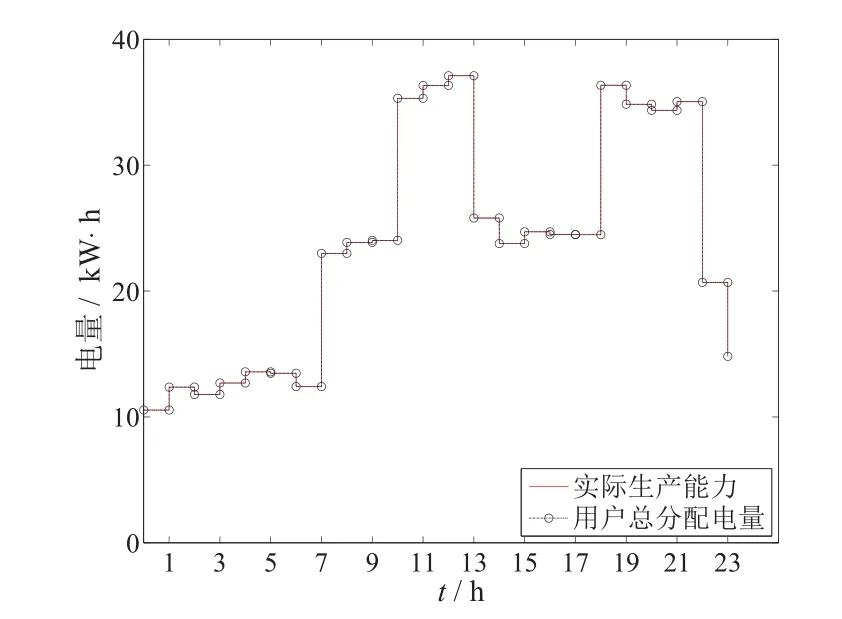
图4 基于非光滑方程组方法的每时段总分配电量Fig.4 The total power distribution per time interval based on non-smooth equations method

图5 基于非光滑方程组方法与传统固定电价方法的社会效益Fig.5 The social benefit based on non-smooth equations method method and traditional fixed price method
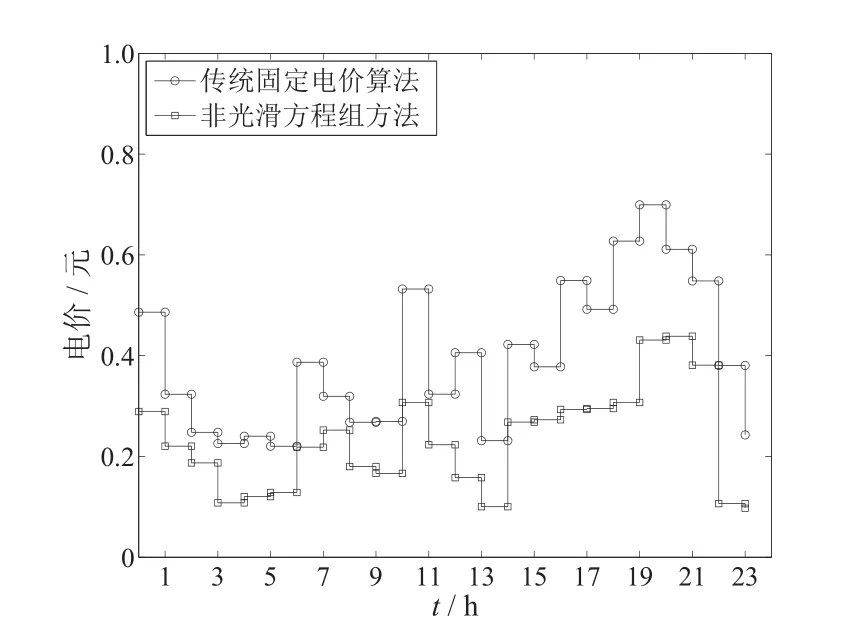
图6 基于非光滑方程组方法与传统固定电价方法的短时段电价Fig.6 The short time interval price based on nonsmooth method and traditional fixed price method
从图3和图4可以看出,当实际生产的电力资源被完全分配时,资源得到最优配置.从图5和图6可以看出,与固定电价方法相比,新方法得到的社会效益要略高于固定电价方法,但是新方法计算的电价更低.这是因为每个用户对电量消费水平的满意程度不同.固定电价方法倾向于平均分配电力资源,没有考虑用户的电量消费水平满意度;而新方法考虑了用户的电量消费水平满意度,优先分配满意度高的用户,所以在社会效益相近的情况下,利用新方法得到的电价更低.该结果与文献[9,10]中的结果相符,所以利用新方法解决智能电网实时定价问题是有效可行的.
5 结束语
本文采用影子价格为智能电网实时定价的基础,首次将非光滑方程组应用到智能电网实时定价问题.利用非光滑方程组解决实时定价问题的优点在于能够同时得到每个时段电力资源的最优配置和实时基础价格.在非光滑方程组中,实时价格是一个重要变量,不再是最优配置问题的附属变量.本文采用了修正拟牛顿法解非光滑方程组,优点是速度快,收敛性好,数值结果稳定.通过仿真模拟结果可以看出,虽然新方法的实时价格要比固定电价的价格低,但是社会效益却几乎相同,而且新方法下的社会效益还比固定电价方法下的略高.所以新方法的实时定价更合理.通过数值结果也验证了利用新方法解决电量最优配置和实时定价问题是可行的.本文对进一步研究智能电网短时段实时定价机制提供了基础理论依据.

