资本积累的空间溢出效应研究
吴继贵,叶阿忠,张月玲
(福州大学经济与管理学院,福建福州350108)
1 引 言
物资、人力和R&D资本是经济增长的重要源泉.资本在地区的禀赋程度、结构组成和流动特性直接决定了地区经济的发展水平.安虎森[1]指出,经济活动存在异质性,且是在特定的空间范围内联系起来的.因此,在空间经济学视域下,不同地区的资源禀赋、资本积累、地理区位、市场条件和政府政策存在一定的差异,导致区域间的资本溢出效应亦表现出不同的特征.也就是说,区域间资本的空间分布和空间影响往往是具体的、块状的和局部的,并非全局的和同质的.然而,既有研究却普遍偏重于全局性分析,假定区域间的资本分布及其溢出具有同质性,致使局部性的经济作用规律被忽视,无法有效甄别特定区域内资本要素的空间溢出机制差异,难以为区域经济一体化发展提供针对性建议.因此,在区域经济发展存在不均衡的条件下以及区域经济一体化进程加快的大背景下,探讨经济区域间资本积累的空间集聚和外溢特性,弄清资本在具体经济区域内部的作用机制,将能够为促进区域间经济的协调发展和整体经济效益的提高,提供科学的理论依据和数据支持,为区域间经济发展政策的制定提供一定的参考和借鉴.
资本空间溢出的相关问题,一直是国内外学术界研究的热点.目前关于人力、R&D和物资资本的空间溢出规律的研究大致可以分为三类.1)关于人力资本空间溢出的研究.Pede[2]指出一个地区的生产效率不仅受地区本身人力资本水平的影响,还受到周边地区人力资本的溢出影响.陈得文[3]和逯进[4]对中国经济问题的经验研究也表明,人力资本在空间上存在正向的溢出效应;2)关于R&D资本空间溢出的研究.Eberhardt[5]和盛垒[6]指出R&D的溢出作用同样不可忽视.Moreno[7]对175个欧洲地区的研究显示,一个地区的知识生产同样会受到其它地区知识的空间溢出影响.Deltas[8]的研究显示,R&D的空间溢出存在一个有效距离.当从溢出中心到接收地的距离为500 km时,R&D的空间溢出效果将被削弱55%∼70%.其他学者亦有类似的发现,例如Krugman[9]、L´opez-Bazo[10]和刘舜佳[11]等;3)关于物资资本空间溢出的研究.Lall[12]指出交通运输基础设施的建设可以冲破地域的限制,并由此产生空间溢出.Tong等[13]对美国交通基础设施的空间溢出性进行了研究,指出基础设施建设不仅能够促进当地的农业产出,还能够对周边地区的农业产出产生影响.Yu等[14]的研究结果显示,中国交通运输具有正向的空间溢出效应.但是,在不同时段,东、中和西部地区的溢出效应又表现出不同的规律.张光南[15]的研究则表明,基础设施的空间溢出对制造业的成本效应远大于地区内部建设所产生的成本效应.这些研究局限于资本外生的理论框架,主要考量单一资本要素的溢出效果,而忽视了资本要素之间的内生影响.因此,对资本溢出效应规律的解读过于宽泛,难以针对特定区域给出具体而富于指导性的政策建议.
关于资本内生关系的研究,当前国内外文献主要沿时间维度展开,从理论和实证两个角度考察人力、物质和研发资本之间的交互影响.1)就理论研究而言,该方面的研究最早始于物资和人力资本关系的探讨.Lucas[16]和Greiner[17]指出人力和物资资本存在一定的互补关系,二者的增长必须相互匹配才能促进产出的增加.Caballé等[18]认为物资资本的增加能够影响人们对教育的时间投入,并由此导致人力资本积累水平的变化.而人力资本水平的变化又会致使边际生产率产生变化,继而对物资资本的积累产生影响.随后,又有学者将R&D引入内生模型,如Funke[19]、Strulik[20]和Arnold[21]建立了以人力、物资和R&D资本的内生增长模型.此后,国内也出现了少量类似的研究.例如,吴春力等[22]构建了出了人力、物资和R&D资本的内生经济理论模型,从理论上论证了三者的动态关系,并指出R&D资本的累积能够较为明显地促进人力资本、物资资本和社会产出的同步增长.2)也有学者试图从实证角度探讨资本之间的内在数量关系.胡永远等[23]采用了GMM估计法,探讨人力资本与物资资本二者间的内生关系.其研究成果表明,人力资本和物资资本的相互影响具有非对称性.Grier[24]对撒哈拉地区的研究同样也表明人力资本和物资资本存在内生性.李志宏等[25]的研究则表明R&D与资本积累之间存在长期且稳定的双向Granger因果关系.魏下海[26]的研究表明受外部区域的竞争优势和经济增长集聚效应的影响,容易导致经济资源和生产要素外流,并指出技术要素和物资资本更容易向人力资本高的地区流动和汇集.遗憾的是,这些研究普遍基于古典统计和计量经济学分析中样本相互独立的基本假设,忽略了个体的空间差异性.从新经济地理学的角度看,任何经济现象都很难摆脱相互之间的空间影响而孤立存在.因此,不考虑空间滞后所产生的影响,显然难以完全反映客观实际.
纵观上述研究,既有文献主要侧重于从全局的角度探讨人力、物资和R&D资本积累的空间溢出规律,而很少从局部的视角研究资本积累在特定区域内的相互作用.同时,以往的研究主要从时间维度探讨人力、物资和R&D资本积累的内生关系,而缺乏从空间维度更深入地解读资本之间的交互影响,导致资本在空间层面的作用规律长期被忽视.为此,本文设计了能够从空间维度反映内生关系的空间计量模型——横截面数据半参数空间结构向量自回归模型,并以上海的一阶和二阶Queen邻近区域为研究对象,探索人力、R&D和物资资本积累的空间集聚和溢出规律.该模型将传统的向量自回归模型的思想应用于空间建模领域,融合了参数估计和非参数估计的优点,对空间经济现象的解读更具系统性和客观性,因而也更切近区域经济现实.本文的研究发现东部和部分中部地区是三种资本积累的热点区域,而西部则为冷点区域;同时,对上海与周边地区资本积累交互影响的分析发现,上海地区R&D资本积累的集聚效应大于扩散效应,对周边地区R&D资本具有虹吸效应;人力资本积累的涓滴效应显著,能够对周边地区的人力资本产生扩散作用;而物质资本积累的空间溢出则呈现出“断裂性”和“跳跃性”,即其在一阶空间邻近“中心效应”显著,而在二阶邻近则“涓滴效应”突出.
2 模型估计、设定和变量说明
2.1 模型估计
本文所设计的CSSSVAR模型,结合了参数估计和非参数估计.它既能够反映出变量之间的线性关系,又能够反映出外生变量出现非线性的情况.设CSSSVAR模型的第k个内生变量方程为
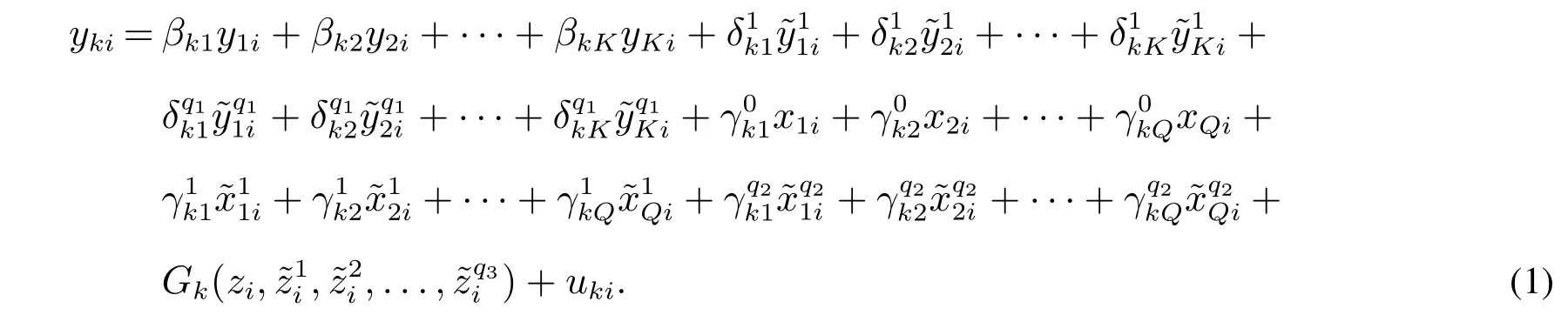
将式(1)中的非参数项移到方程左侧,可得
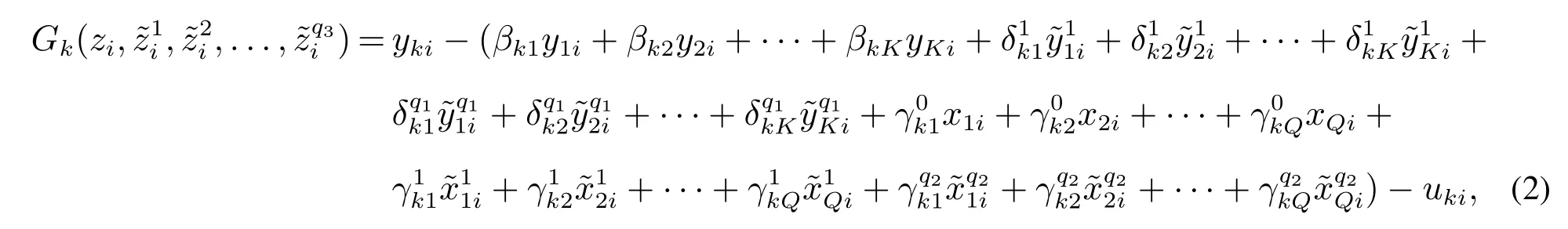
其中yki表示第i∈{1,2,...,N}个个体的第k∈{1,2,...,K}个内生变量,表示i个个体第K个内生变量的一阶空间滞后;xQi表示第i个个体的第Q个外生变量,表示i个个体第Q个外生变量的一阶空间滞后;zi是第i个个体非参数部分的外生变量,表示i个个体非参数部分外生变量的一阶空间滞后;是非参数项;uki为噪音,假定其为独立同分布,且
若β,δ和γ给定,则式(2)可以写成

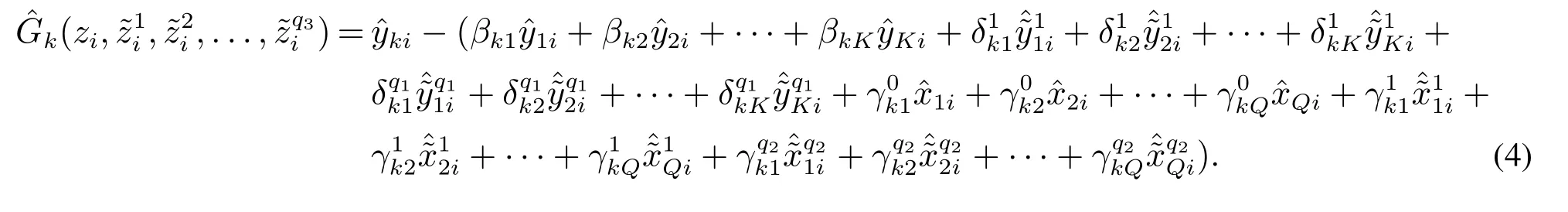
将式(4)代入模型(1),得到如下参数模型

通过GMM估计方法[28],可以得到β,δ和γ参数的估计结果.接着,可以获得Gk(·)的最终估计

2.2 模型设定
式(7)∼式(8)中的变量包括R&D(RD)、物资资本(KC)、人力资本(LC)和对外开放度(Open).有研究表明,Open与这些变量有可能存在不同程度的非线性关系.例如,赖永剑[31]应用PSTR模型验证了R&D、人力资本、基础设施和贸易开放度之间存在较为明显的非线性的关系.同时,通过绘制RD、LC、KC与Open的散点图(图1),亦存在类似的发现.
此外,各资本关于Open的非参数估计与Open的拟合曲线同样再次印证了此种非线性关系(图6).由此,可以给出以RD、KC和LC为内生变量,以Open为非参数外生变量的半参数空间结构向量自回归模型的完整形式.该模型不仅考虑到了地区自身资本积累的影响,还考虑到了一阶空间邻近和二阶空间邻近地区资本积累对当地所产生的影响.

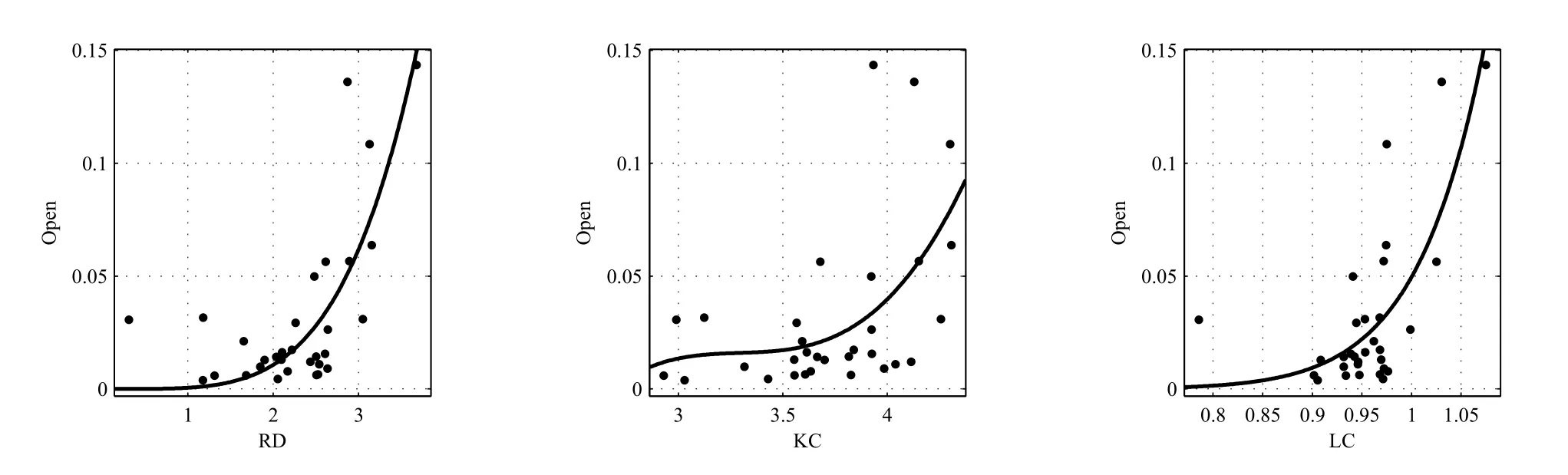
图1 RD,KC,LC和Open的拟合曲线Fig.1 The fitted curve among RD,KC,LC and Open
需要说明的是,模型(7)中内生变量的空间滞后阶数,主要根据赤池信急准则(akaike information criterion,AIC)进行判定和选择.此处主要采用了由Akaike[32]和McQuarrie等[33]所提出AIC、AICc和AICu三个评判标准.表1列出了信急准则计算结果.
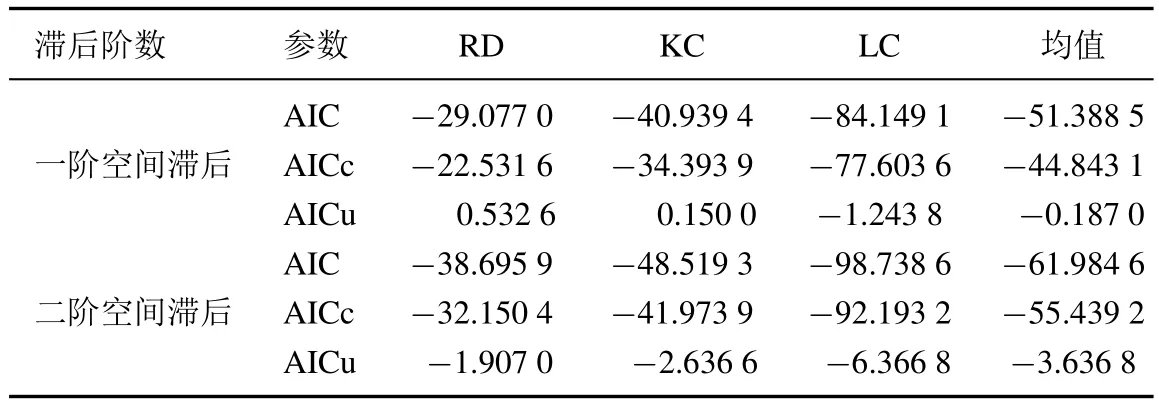
表1 信息准则计算结果Table 1 The results of AIC
计算结果表明,较一阶空间滞后,在二阶空间滞后的条件下,所构建的半参数空间结构向量自回归模型模型具有更好的估计性质.
在模型(7)中,若将RDki,KCki和LCki,k=1,2,3,移到向量方程的左侧,便可获得由三者所构成的向量系数矩阵β.若将其求逆矩阵,并通过矩阵运算将其移到向量方程右侧,将各变量的系数矩阵与β矩阵的逆进行矩阵运算,则可以获得简化后的向量方程,具体如式(8)所示.

其中γ=β−1σ,η=β−1θ,M(Openi)=β−1G(Openi),且v=β−1u.
2.3 变量说明
本文各变量的构造说明如下:1)R&D资本主要采用永续盘存法测算.考虑到R&D水平的地区差异,此处借鉴王孟欣[29]的做法将东、中和西部地区的R&D折旧率分别设为18%,15%和12%;2)物资资本的计算参考了单豪杰[30]的做法,并将折旧率设为10.196%;3)由于教育在人力资本的形成过程中起着至关重要的作用,且与人力资本表现出很强的正相关关系.因此,人力资本的计算主要采用教育年限法;4)对外开放度则采用进出口总额占GDP的比值进行衡量;5)空间关系矩阵则根据Queen准则进行构建.其中,一阶Queen邻近表示某区域具有共同边界或者共同顶点的邻近,而二阶Queen邻近表示某区域周边具有共同边界和顶点的邻近.由此,构造出中国31个省市的一阶和二阶Queen邻近,具体如图2所示.需要说明的是,除Open变量外,其它变量在估计前均进行了对数化处理.构造上述变量的数据主要来源于《中国统计年鉴》、《中国科技统计年鉴》和《中国人口与就业统计年鉴》.

图2 基于Queen准则的空间一阶邻近和二阶邻近的空间关系矩阵Fig.2 The first and second orders of spatial neighbors based on Queen criteria
3 实证分析
3.1 全局的空间相关性
考虑到所构建的CSSSVAR模型同时包了括一阶和二阶的空间邻近关系.因此,有必要分别对基于一阶Queen和二阶Queen空间权重RD、KC和LC变量对应的Moran指数进行计算,以确定各类资本是否存在空间相关性.其中,基于一阶Queen空间权重的RD、KC和LC变量的Moran指数的计算结果分别为0.357 7,0.372 5和0.313 6,且其所对应的P值分别为0.001 0,0.001 2和0.002 0(图3).检验结果表明,在一阶Queen条件下,R&D资本、物资资本和人力资本均表现出很强的正空间相关性.在二阶Queen条件下,RD、KC 和LC变量的Moran指数分别为0.176 2,0.203 4和0.129 1,对应的P值分别为0.001 5,0.003 1和0.026 3(图4).虽然,在二阶Queen条件下,各资本的空间相关性较一阶Queen情况下有所减弱,但是依然表现出较强的显著性.

图3 基于一阶Queen的RD、KC和LC的Moran散点图Fig.3 The Moran scatter of RD,KC and LC based on the first order of Queen
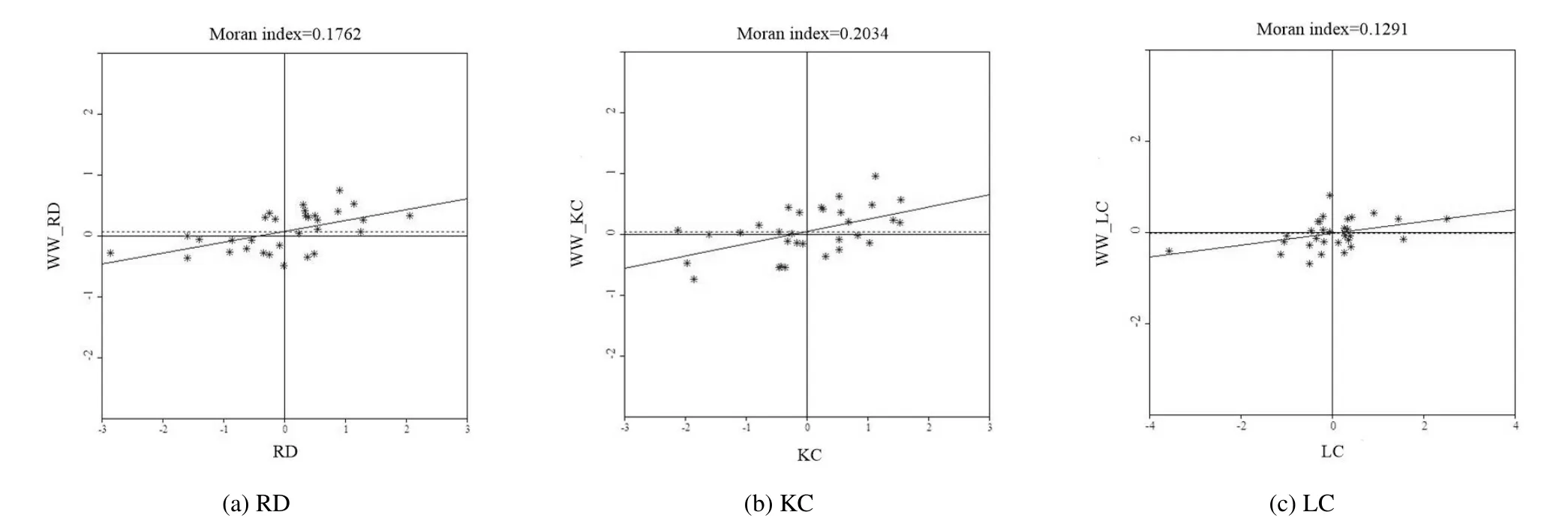
图4 基于二阶Queen的RD、KC和LC的Moran散点图Fig.4 The Moran scatter of RD,KC and LC based on the second order of Queen
3.2 局部的空间相关性
虽然,Moran指数能够从全局上判断R&D资本、物资资本和人力资本的空间相关性,但是却无法识别它们在局部空间上的集聚(局部空间相关)模式.而G统计量恰巧弥补了这方面的不足,它能够识别出空间个体属性是存在高值还是低值集聚,即所谓的热点(hot spot)和冷点(cold spot)区域.由图5可知,1)R&D 资本积累主要在上海、江苏、安徽和天津地区表现出高值集聚.这些地区是我国R&D投资热点区域.然而,新疆、青海、甘肃和四川地区的R&D资本积累则表现低值集聚,是我国R&D投资的冷点区域,R&D投资的活跃度相对较低;2)物资资本的热点区域主要分布在东部及其毗连地带.这些地区包括上海、浙江、江苏、福建、山东、河南、安徽和江西.然而,物资资本的冷点区域则主要分布西部地带,其中包括新疆、甘肃和四川;3)人力资本热点地区主要位于天津和河北两地,空间分布范围相对较小.然而,冷点区域主要集中于西部地区,空间分布范围相对较大,面积近乎覆盖了三分之一的国土面积,主要包括新疆、青海、西藏、四川和广西地区.上述现象表明,我国R&D资本、物资资本和人力资本的积累存在较为明显的空间分异和块状分布的现象,即总体上表现出东部地区的资本积累水平相对较高,而西部地区的资本积累水平则相对较低.根据经济生产函数,资本积累水平的高低将直接影响到地区的经济产出[35].由此可见,西部地区R&D资本、物资资本和人力资本的欠缺,是导致其经济发展长期落后于东部和部分中部地区的重要原因.
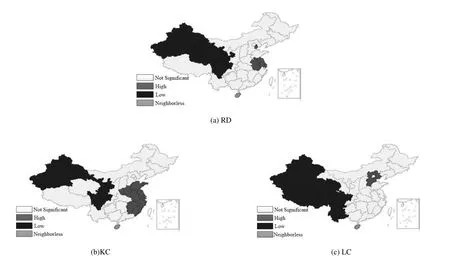
图5 RD、KC和LC的空间集聚图Fig.5 Spatial agglomeration of RD,KC and LC
3.3 估计结果
根据式(1)∼式(6)的估计过程,此处估计出了由人力资本、物资资本、R&D资本和Open四者所构建的实证模型.通过使用MATLAB和R等软件,得出了模型中的参数部分和非参数部分的估计结果.其中参数部分的估计结果如表2所示,而非参数部分的估计结果如图6所示.

表2 CSSSVAR模型的估计结果Table 2 The estimation results of CSSSVAR model

续表2Table 2(continue)

图6 R&D,KC和LC关于对外开放度(Open)的偏导数p1,p2和p3Fig.6 The curve fit of the partial derivative of openness p1,p2and p3.
3.4 空间脉冲响应
该部分内容主要以上海及其周边地区作为研究对象,模拟在上海地区的资本冲击条件下,其一阶Queen和二阶Queen空间邻近地区的资本响应情况(图7).

图7 上海的一阶与二阶Queen空间邻近区域Fig.7 The first and second orders Queen neighbors of Shanghai
图7中上海的一阶Queen邻近区域为江苏和浙江,而二阶Queen邻近区域由北往南依次为山东、安徽、江西和福建.
在图8∼图10中,各图的横坐标表示省份,从左往右依次为浙江−1、江苏−2、安徽−3、福建−4、江西−5和山东−6,而纵坐标表示脉冲响应值.

图9 上海地区KC冲击下其周边地区KC的脉冲响应值Fig.9 The neighbor’s impulse response value of KC under the shocks of KC from Shanghai

图10 上海地区LC冲击下其周边地区LC的脉冲响应值Fig.10 The neighbor’s impulse response value of LC under the shocks of LC from Shanghai
根据图8,对来自上海地区R&D资本的正向冲击,上海的一阶与二阶Queen空间邻近区域的R&D资本表现出“U”形的负向响应.其中,浙江、江苏和江西的负向响应幅度相对较小,脉冲响应值分别为−0.100 6,−0.082 1和−0.089 5,而安徽、福建和山东的负向响应幅度相对较大,脉冲响应值分别为−0.179 0,−0.173 4和−0.120 7.该结果表明,上海地区R&D资本的积累存在负向的空间溢出效应,即上海的R&D资本的积累能够在不同程度上抑制周边地区R&D资本积累水平的提高,表现出较为明显的中心化效应和极化效应.这主要是由于,凭借独特的地理区位、劳动者素质、产业结构和对外贸易政策方面的优势,上海对高科技产业的吸引能力不断增强,并在区域中逐步形成了独特的竞争优势,对周边地区的R&D资源产生了较强的吸引力,尤其对其二阶Queen邻近的安徽、福建和江西地区的R&D资本所产生的吸引力更为明显.这些吸引又具体表现为上海周边地区R&D人才的流失、R&D资金的流失和R&D成果的流失.该发现也在一定程度上验证了齐红倩等[34]的研究结果,即上海地区的自主创新活动存在“技术洼地效应”.随着上海自贸区建设的推进,资本要素的流动将更为通畅.因此,在可预见的时期内,上海地区R&D资本的中心化效应和区位锁定效应显著,且尚处于强化阶段,短期内难以逆转.
根据图9,对来自上海地区物资资本的正向冲击,上海的一阶与二阶Queen空间邻近区域的物资资本表现出不同幅度的响应.其中,一阶Queen空间邻近区域表现出负向响应,而二阶Queen空间邻近区域则表现正向响应.这表明上海地区物资资本的积累能够对其毗连地区的浙江和江苏省的物资资本产生一定的抑制作用.但是,其对二阶Queen邻近的安徽、福建、江西和山东的物资资本则表现出正向的空间溢出效应.由此可见,上海地区物资资本的积累的空间溢出效应表现出一定的“断裂性”和“跳跃性”.这主要是由于,在上海的一阶Queen邻近区域,即浙江和江苏地区的物资资本的积累存在一定的同质性,区域内对物资资本投资更多地表现为竞争关系.由于上海地区具有良好的经济基础、更为开放的投资环境以及成熟的资本市场等优越条件,因而能够对周边的物资资本投资形成巨大的吸引力,易产生回波效应,诱导周边的物资资本向上海地区聚集.而这在一定程度上抑制了浙江和江苏两地物资资本积累水平的提高.然而,与浙江和江苏地区不同的是,处于上海二阶Queen邻近的安徽、福建、江西和山东地区,上海地区的物资资本则对这些地区表现为正向的空间外溢性,即对这些地区物资资本的扩散效应更为显著.出现此种现象的原因可能包括这几个方面:首先,二阶Queen邻近地区的地理位置相对于一阶Queen邻近地区相对较远,这些地区的物资资本投资受上海的影响相对较小.同时,这些地区在各自所属的区域中的经济实力相对较强,因此其对周边的物资资本投资也存在较强的吸引力.其次,不像江苏、浙江与上海地区的经济发展实力相当,二阶Queen邻近地区的经济实力与上海地区的经济发展水平存在一定的差距,在区域的固定资产投资中更多表现为区域互补和带动的关系.例如,上海地区在固定资产投资、研发和管理占据较高的优势,而安徽、福建和江西等地区则在固定资产建设的人力和成本方面占据优势.
根据图10,对来自上海地区人力资本的正向冲击,上海的一阶Queen邻近和二阶Queen邻近地区的人力资本均表现出明显的正向响应,且响应强度随着距离上海邻近阶数增加而衰减.具体而言,在一阶Queen邻近范围内,上海对江苏和浙江地区的人力资本的溢出效应最为明显,其响应幅度分别位居第一和第二.在二阶Queen邻近范围内,上海地区对安徽和福建的人力资本溢出较为明显,山东次之,江西则最弱.该结果提示,上海地区的人力资本积累能够对周边地区产生不同程度的涓滴效应,处于资本积累的扩散阶段.这与上海的人口结构、经济圈建设、产业结构调整以及教育资源存在密切的关系.其中1)从上海的人口结构来看,上海地区的流动性人口数量巨大,这意味着上海地区的人力资本具备较高的溢出潜力.根据《上海统计年鉴2013》发布的数据,2012年上海流动人口数量达到960万人,全市的常住人口和流动人口的比重达到40.3%.而流动性人口的最大特征具有非稳定性,这部分人在上海地区学到技术和本领后,很可能会选择人才竞争相对较为缓和的周边地区进行发展;2)从经济圈的建设来看,随着长三角快速交通网络的建设,形成了以上海为中心的“1小时经济圈”,并逐渐向“2小时经济圈”和“3小时经济圈”的方向发展.上海与浙江、江苏经济发展的同日化和同城化,在很大程度上推动了区域间的人口流动,促进了上海地区人力资本的外溢.由此,也就不难解释为何上海的一阶Queen邻近地区人力资本响应幅度远大于二阶Queen邻近地区的现象;3)从产业结构调和地区发展战略上看,上海已经处于工业化后期,并向后工业化阶段转变,其经济结构以服务业为主.同时,政府为了将上海建设成国际经济、金融、贸易和航运中心,上海市正逐渐将低端产业和部分高新技术产业向周边地区进行转移.而产业转移既能够拉动周边地区经济的增长,又能够通过“干中学”效应为周边地区的人力资本的积累做出贡献;4)从教育资源上看,上海地区高校云集,是我国高等教育最为发达的地区之一.优质的教育资源能够培养出地区社会经济发展所需的各类人才.在为周边地输送了大量高素质的人力资源的同时,上海地区的教育改革和人才培养模式的探索也为周边地区人才培养和教育改革起一定的示范作用.
4 结束语
资本在空间层面的分布特征和作用机制蕴含着区域间资本的重新配置和重组的政策含义.本文的实证研究结果表明:1)就全局性的角度而言,在平衡东西部地区的发展时,一方面需要注重对西部地区的物资资本和研发资本的投入,另一方面也要注重对该地区人力资本的培养.同时,邻近区域若要充分发挥资本的空间溢出性,就必须充分考量资本在区域间的配置水平和配置结构,即空间相互邻近区域的资本水平和资本结构组成的差距不宜过大.2)就特定区域的角度而言,资本的作用又有具体的形式和规律.本文对上海及周边地区的研究表明,在不同的空间领域内资本的集聚和溢出过程并非单线程,而是多线程并存的形式.因此,在制定特定地区的资本配置政策时,需要弄清资本,尤其是区域增长极对周边地区的资本,是处于集聚作用阶段、溢出作用阶段还是二者作用交织并存的阶段.唯有如此,在推进区域一体化发展的进程中,不至由于过度的“马太效应”和“极化效应”而导致区域内部发展出现明显的断裂地带、边缘区域和凹陷地区,进而实现特定区域内部社会经济的协调发展和整体实力的提高.

