超精密车床主轴回转误差影响因素研究*

张根明

(广东工业大学 机电工程学院，广州 511400 )

0 引言

超精密主轴是超精密机床的关键技术之一。主轴回转误差是影响机床加工精度的主要因素[1-3]。超精密主轴回转误差测量能将主轴的各项误差如回转误差、圆度误差很好地反应出来，对主轴向更高精度的迈进具有重大的意义。

由于主轴本身的圆度误差很大，如果以主轴为基准，直接对其进行测量，回转误差往往被基准本身的误差掩盖，很难检测到。因此需要一个圆度很高的标准球安装到主轴对其进行测量。虽然标准球的圆度误差很小，但相对于要测量的回转误差达到微米级甚至更小，仍然不可忽略，这时需要引入一种方法将圆度误差和回转误差分离开来。

目前超精密主轴回转误差主要的测量方法有反转法、两点法、三点法、多点法、多步法等。反转法[4]在测量过程中标准球和传感器要旋转180°，这样会带来一定的安装误差，从而导致测量的精度。三点法[5-6]是将三个传感器按照一定的角度分布在标准球的同一截面，但是传感器之间的角度设定存在误差，而且需要3个高精度的传感器，增加了测量成本。本文主要对测量过程中标准球和传感器产生的安装误差原理进行分析，用双向测量法[7]对超精密车床主轴进行试验，多步法[8]对实验数据进行分离，得到气浮主轴不同转速下偏心对回转精度的影响情况，并进行归纳。

1 标准球偏心的产生及影响

1.1 标准球安装偏心的影响

主轴在测量过程中包含3种误差：安装偏心误差、标准球圆度误差、主轴回转误差。现有的测量方法都是将标准球的安装偏心误差用虑一次谐波[9-10]的方式将其去除掉，再对剩余的圆度误差和回转误差进行分离。实验表明当安装偏心过大时会引入二阶谐波分量叠加的误差，这时时去除不掉的，因此实验之前必须保证标准球的安装偏心足够小。

如图1所示，我们假设回转轴的轴心为O,标准球的轴心为O′，它们之间的偏差值为L。当主轴做圆周运动时，标准球做偏心运动,偏心为L。实际测量值(传感器到标准球的距离)为R,S1测的是传感器到主轴圆心纵坐标的距离，S2测的是传感器到主轴圆心横坐标的距离：

S1 =R+Lcosθ

(1)

S2 =R+Lsinθ

(2)

对测量数据进行频域分析，在频域图中谐波出现的阶次越多，最终显示的圆越不规则且棱角越多。从式(1)和式(2)可以看出传感器到主轴圆心的距离随转位角θ的变化而变化，变化的程度由偏心量的大小决定。变化关系如图2、图3所示。图2显示的是安装偏心为15μm时的测量图形，图3显示的是安装偏心为0.9μm时的测量图形。从图2可以看出测量图形是一个棱角分布很明显的不规则的圆，棱角的峰值大小由偏心量L值决定，L越大棱角越突，L越小棱角越平。那是因为偏心量过大时会带来二阶甚至二阶以上的谐波分量叠加在传感器读取的数据里，对分离的精度影响较大。从图3可以看出，当偏心减少时，测量出的图形棱角明显减少，安装偏心所带来的谐波分量也明显减少，对分离的精度影响减少。

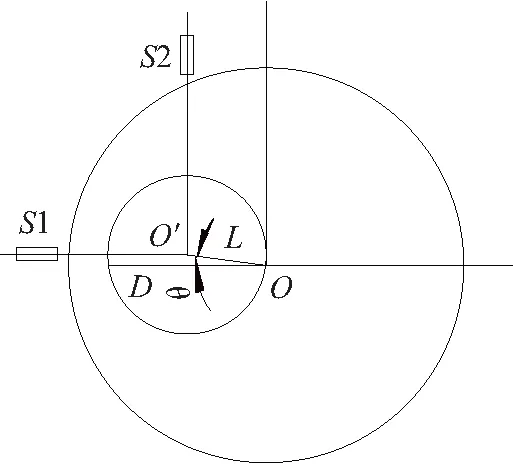
图1 标准球安装误差示意图

图2 15μm偏心作用下测量图形

图3 0.9μm偏心作用下测量图形

1.2 标准球调偏

为了提高回转误差的分离精度，我们采用了高精度的标准球，调整主轴和标准球的偏心装置如图4所示。在主轴的最前端装一个真空吸附的装置，将标准球吸在上面，此装置便于标准球的安装与位置的调节，再用德国Mahr测量仪(高精度电容位移传感器，分度值为0.0001mm)的探头打在标准球的表面。转动主轴，看标准球在转动一圈中测量仪显示屏上面的示数变化。找到示数最大的点和最小点，用胶锤轻微的敲示数最大点的标准球底部的截面，每次敲击后的值等于敲击前的最大值减去最大值和最小值差值的一半，如此反复敲击直到标准球在转动一圈中最大值的最小值的差值在0.9μm以内。此时主轴和标准球的偏心为0.9μm。

图4 标准球偏心调整装置

2 传感器偏差的产生及影响

2.1 传感器偏心的影响

传感器的安装误差指的是传感器正对标准球一截面的轴线方向的偏差量。理想的情况是传感器的轴线正对标准球的XY轴，可实际安装过程中总会出现各种因素使传感器的轴线偏离标准球的XY轴，偏离的程度越大对测量的精度影响越大。如图5所示。S1传感器为理想安装前位置，S2传感器为实际安装位置，S1和S2的距离为L，S1距标准球表面的距离为a，标准球的半径为R，可推出传感器的安装偏差及S1、S2传感器到球心的距离差值D：

(3)

由上式可知，标准球半径不变，传感器安装偏差的影响由a和L决定。a和L值越小，传感器的安装偏差越小。

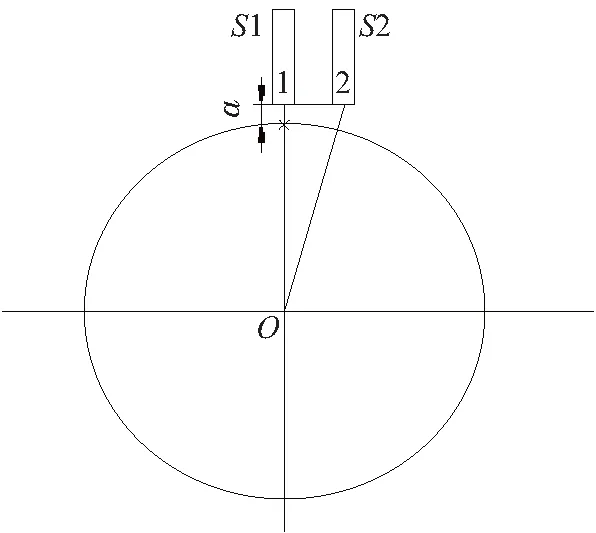
图5 传感器安装误差示意图

2.2 传感器调偏

将其硬件接线如图6接好，接线时应注意：电容位移传感器应一一对应其所在通道，其中3号传感器应放在对应标准球的轴向位置，即Z轴，1号对应X轴，2号对应Y轴。

图6 传感器偏心调整装置

其中1号和2号传感器测量的是主轴径向回转误差，3号传感器测主轴轴向回转误差。

传感器对中。先对中Z轴，在3个传感器通道处各有一个可调螺钉，将3号传感器的可调螺钉松开，传感器靠近标准球，使图7中指针在0附近。刷新，移动支架左右移动直至示数为最大值，则3号传感器左右对好了。再移动上下，方法同上，至此3号传感器已对中。

在调节完Z轴的对中后，将1号传感器退回并将螺钉锁紧固定。将通道改为Y，如图8所示。将2号传感器的可调螺钉松开，传感器靠近标准球，指针在0附近，刷新，调节X轴轴向运动使得指针示数达到最大值。刷新示数，旋转主轴调节示数在10μm以内，锁紧螺钉。将通道改为Z，松开螺钉，将3号传感器靠近标准球指针出现指针示数，刷新，旋转主轴检测偏心在10μm以内，锁紧螺钉。此时测量径向回转误差的传感器全部装好，最后通过可调螺钉调节1号传感器使其指针示数在10μm以内，至此3个传感器的偏心都已调好。

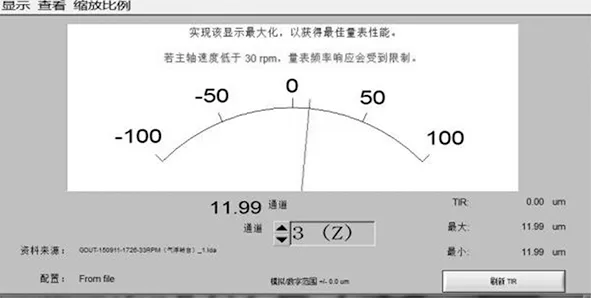
图7 Z轴调中

图8 Y轴调中

3 回转误差分离

对于超精密机床主轴，被测件的形状误差相对于主轴回转误差是不可以忽略的。因此用双向测量法将主轴的误差测量出来，再用多步法对圆度误差和回转误差进行分离。

双向测量法的原理如图9所示：使用两个电容传感器分别测量主轴X,Y方向的径向误差。利用前面的装置，保证两个电容传感器X,Y安装方向相互垂直;传感器距离主轴被测表面约10μm，两个测头分别测量主轴的X和Y方向的回转误差。

将测量得到的数据用多步法进行误差分离。多步法又称闭合等角转位法，它通过主轴不断地旋转，在标准球一周均匀采N个点，各测量角度差为θ。每个测量数据中都带有主轴的回转误差和形状误差。

θ= 360/N

(4)

由于工件圆度误差具有严密的周期性，其在全周各等分测位上采集到的数据之和因对称状而对消，因此主轴回转误差eθ为：

(5)

图9 双向测量法原理示意图

为了验证本文测量方法和误差分离方法的可靠性，我们使用美国Lion回转误差分析仪对超精密车床主轴进行测量。测量结果如图10、图11所示。

图10 回转误差时域图

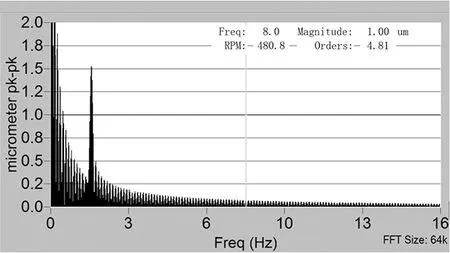
图11 回转误差频域图

图10为回转误差时域图，可以看出采用本方法测得的偏心和回转误差很小，其中回转误差只有0.69μm。证明了该方法的可靠性。图11为回转误差频域图，可以看出采用本方法产生的谐波阶次几乎都是一次的，这利于分离圆度误差和回转误差。

经过反向法分离后不同转速下气浮主轴偏心量对回转精度的影响如表1所示。

表1 不同转速下回转精度变化表

从表中可以看出在同一转速下偏心越大回转精度越差，那是因为偏心增大时会引入一阶以上的谐波分量，影响数据处理。在偏心相同时，主轴转速越高回转误差精度越高，因为主轴刚启动时转速为达到稳定，导致主轴里面的气体不均匀从而精度不高，随着转速越来越高，气体轴承趋于均匀，精度越好，最终达到稳定。

4 结论

本文对超精密车床主轴回转误差测量过程中标准球和传感器偏心的产生和对测量结果带来的影响进行了深入分析。运用多步法得到主轴在不同转速下偏心对回转精度的影响，得出了转速和偏心对气浮主轴回转精度的影响趋势，为检测主轴回转误差提供理论依据。由于本方法测得的误差非常小，适用于对精度要求非常高的场合。