“种子”的力量

杨世华

中考复习是对初中所学知识点的整体梳理过程和对知识应用的熟练和深化阶段.如何把初中所学宠大、繁杂的知识系统科学合理地梳理成简洁而又简单的，易于学生记忆、理解、掌握的知识体系，是教师在复习教学中难以攻克的难题.怎样解决这个难题呢？下面以方程、不等式、函数的复习为例，谈谈我的看法.

谈到对方程、不等式和函数的认识，大家会想到通过函数，运用数形结合思想建立起方程、不等式与函数之间的联系.

认真想一想，这样做是把方程、不等式及函数看成了独立的个体，再通过函数建立起几个个体之间的联系.如何才能真正建立起它们之间本质上的联系呢？

如果把方程、不等式及函数这一知识体系比作一棵繁茂的大树，那么这棵繁茂的大树只源于一颗种子.现在，我们通过寻找一元一次方程、一元一次不等式及一次函数这棵大树的种子的过程再次认识方程、不等式、函数之间的联系，从而把繁杂的知识点梳理得简洁而又简单.

一元一次方程：只含有一个未知数、未知数的最高次数为1且两边都为整式的等式叫做一元一次方程；使方程左右两边的值相等的未知数的值，叫做方程的解.其一般形式为：ax+b=0（其中a、b为常数，a≠0）；

一元一次不等式：含有一个未知数，并且未知数的次数是1的不等式叫做一元一次不等式；使不等式成立的未知数的值叫做不等式的解.不等式的所有解组成这个不等式的解集.其一般形式为：ax+b>0或ax+b<0（其a、b为常数，a≠0）；

一次函数：一般地，形如y=kx+b（k、b是常数，k≠0）的函数叫做一次函数.其中x是自变量，y是因变量，k为一次项系数，y是x的函数.我们也可以把它写成y=ax+b的形式，其中a=k.

观察上面三个数学式：

ax+b=0

ax+b>0

y=ax+b

一元一次方程ax+b=0是研究当x取何值时，代数式ax+b的值为零；一元一次不等式ax+b>0或ax+b<0是研究当x取何值时，代数式ax+b的值为正或为负；一次函数y=ax+b是研究随着自变量x值的变化，代数式ax+b的值的变化情况.我们会发现，原来初中阶段我们学习的一元一次方程、一元一次不等式、一次函数这一繁杂的知识体系，只是研究ax+b这个代数式的值与x的值之间的关系.也就是说，我们只是系统地学习了ax+b这一个代数式.从这个角度看，原来学习的一元一次方程、一元一次不等式、一次函数就显得尤为简单、简洁了.而ax+b这个代数式就是一元一次方程、一元一次不等式、一次函数这棵繁茂大树的种子.

在复习中，教师要积极引导学生透过繁杂的知识认清知识间的内在联系，这样复习能使学生将知识融会贯通；这样复习能让学生掌握认识事物的一般规律（从特殊到一般）；这样复习既简化了知识，方便了记忆，又深化了理解，更利于应用.

下面，我们再通过数形结合的方法，形象地观察ax+b的值与x的值之间的关系.

我们知道，x与ax+b相对应的值作为点的坐标，在平面上的点集是一条直线.其图像如图所示：

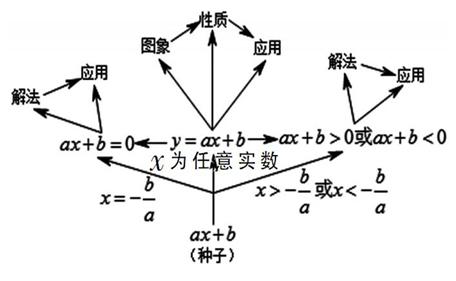
从图中我们可以看出，x0是代数式的值为0时对应的x的值.也就是说，x0是一元一次方程ax+b=0的解；x< x0是代数式ax+b的值小于0时，对应的x的所有值组成的集合，也就是一元一次不等式ax+b<0的解集；x>x0是代数式ax+b的值大于0时，对应的x的所有值组成的集合，也就是一元一次不等式ax+b>0的解集；而一次函数y=ax+b则是全面讨论x为全体实数时与代数式ax+b的值的对应情况.从中我们能看到一元一次方程、一元一次不等式、一次函数三者的内在联系：研究代数式ax+b的值与x的值之间的对应关系.可以用下图来展示代数式ax+b与一元一次方程、一元一次不等式、一次函数之间的生长关系.

在这个图中我们能清晰地看出一元一次方程、一元一次不等式、一次函数之间的内在联系，从而更好地形成知识网络，使三者浑然一体.

类似地，我们再看一元二次方程、一元二次不等式、二次函数之间的联系，去寻找这棵大树的种子.

只含有一个未知数，并且未知数的最高次数为2的整式方程叫做一元二次方程.一元二次方程的标准形式（即所有一元二次方程经整理都能得到的形式）是ax2+bx+c=0（a、b、c为常数，且a≠0）.

只含有一个未知数且未知数的最高次数为2的不等式叫做一元二次不等式.它的一般形式是ax2+bx+c>0 或ax2+bx+c<0 （a、b、c为常数，且a≠0）.

一般地，把形如y=ax2+bx+c （a、b、c为常数，且a≠0）的函数叫做二次函数，其中a称为二次项系数，b为一次項系数，c为常数项.x为自变量，y为因变量.

不难看出，这一棵繁茂大树的种子是代数式ax2+bx+c.也就是说我们初中学习的一元二次方程、一元二次不等式、二次函数这一繁茂的知识大树，也只是为了研究代数式ax2+bx+c的值与x的值的对应关系（如下图）.

用图来展示代数式ax2+bx+c与一元二次方程、一元二次不等式、二次函数之间的生长关系如下.

从图中我们能清晰地看出一元二次方程、一元二次不等式、二次函数之间的内在联系，从而更好地形成知识网络，使三者浑然一体.

窥一斑而知全豹，很多知识都有着内在的联系，只要善于观察、总结，都能找到那颗种子.

例如，我们在复习“相交线与平行线”时，关于角的概念和性质很多：对顶角、邻补角、平行线的性质与判定等，这些概念和性质看似相对独立，其实他们都是“如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补”这一定理的特殊形式.如图：

通过对这几个图形的观察与理解，它们之间的内在联系及生长点就一目了然了.

学生只要将“如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补”理解透彻，就能很好地把对顶角的性质，邻补角的性质，平行线的判定定理及性质定理等内容构建成一个知识网络.

又如：在复习时，不要就某一道题来介绍它运用了哪一种数学方法，而应该从对各种数学问题的解决中，系统地总结某种数学方法能够解决哪一类数学问题.让学生认识数学思想与方法的重要性：它是一颗种子，放在哪里都会生根、开花、结果.

中考复习时间紧、内容繁杂，如果教师在进行复习教学时懂得发挥“种子”的力量，以此引导学生抓住知识间的内在联系，形成科学合理的知识网络，就能帮助学生将学习过程变得简单而又深刻.

编辑/王一鸣 E-mail：51213148@qq.com