基于RS与SVM的高校教师绩效评估模型的构建与仿真

刘 叶，王 帅，周庆忠

（1.重庆能源职业学院，重庆 402260；2.陆军勤务学院，重庆 401311）

1 引言

目前，随着高等教育事业的不断发展，教育质量受到广泛的关注，具有一支高水平的师资队伍是提高教育质量的有力保障。绩效考评作为评定高校教师工作行为与质量的主要方式，相关研究也在逐渐增多[1-6]。绩效考评是现代企业提升竞争力的有效工具，将其科学运用到高校教师管理当中，能够检查教师履行职责情况，形成良好的激励机制，绩效考评已逐渐成为高校人力资源管理的重要组成部分。因此，构建起符合自身特点的教师绩效考评体系，对于进一步增强高校办学能力、提升教学水平具有重要的现实意义。

支持向量机（SVM，Support Vector Machine）具有良好的理论基础，在处理小样本学习问题上具有独到的优越性[7-8]。粗糙集（RS，Rough Set）对于属性简约具有很好的效果[9-10]，因此，本文综合使用粗糙集与支持向量机，建立了基于RS-SVM的高校教师绩效考评模型，以提高高校教师绩效评价的简便性、科学性和准确性。

2 高校教师绩效考评指标体系的建立

高校教师绩效考评指标体系是绩效考评工作得以开展的基础，科学构建指标体系是高校教师绩效考评的重要准备工作内容。本文建立的指标体系见表1，需要指出的是由于个体差异的普遍性，每个个体都有其独特的个性特征，而不同院校不同学科不同专业的高校教师所处的位置不同，承担的课程性质和对学生的培养目标都有很大不同，这就导致不同的评价指标对不同的教师具有不同的重要意义。因此，在具体对特定专业及岗位的高校教师进行绩效考评时，需要针对实际情况对指标体系进行适当调整。

表1 高校教师绩效考评指标体系

3 基于RS-SVM的高校教师绩效考评模型的建立

3.1 基于RS的评价指标约简

RS理论只能处理离散型数据，对连续型数据无法进行处理，因此，在对评价指标约简之前首先要对指标中的连续属性进行离散化处理。在此基础上，基于RS理论对指标体系进行约简，从而降低模型复杂度。

可以用四元组S=（U,A,V,F）来表达粗糙集中的信息，其中：

U={u1,u2,…,u||U}，是有限非空集合，即论域；

A=，为属性的非空有限集合；

AV=为属性a的值域；

f:U×A→V是一个信息函数，它为每个对象的每个属性赋予了一个信息值，即：

知识表达系统也称为信息系统，通常也用S=(U,A)来代替S=(U,A,V,F)。

如果A=C⋃D,C⋂D≠φ,则可以将(U,A)看作为信息表，C中的属性作为条件，D中的属性起决策作用。

在所有的属性当中，有些属性很重要，有些属性不太重要，甚至有些属性基本没有任何作用。属性约简就是要找到没有任何作用以及作用非常小的属性并将它们剔除，从而降低信息系统的复杂程度。

令R为一族等价关系，P∈R，如果ind(R)=ind(R-{P})，则称P在R中不起任何作用；反之称P在R中具有作用。假如每一个P∈R都在R中具有作用，就证明R是独立的；相反说明R是不独立的。设P⊆R，假如P为独立的，并且ind(P)=ind(R)，就可以将P看做R的约简。

当R的简约不止一个时，可以将所有必要的约简组成一个集合，定义为R的核，可以用core(R)表示。

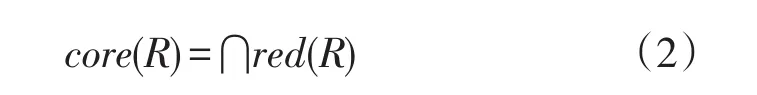
式中red(R)代表R所有的约简。

实际运用过程中，每一个分类对其他分类的作用不同，有的只是有关系，有的却十分重要，程度有很大不同，因此，还必须考虑约简与核的相对性问题。

令P和Q为U中的等价关系，Q的P正域记为Posp(Q)，即：

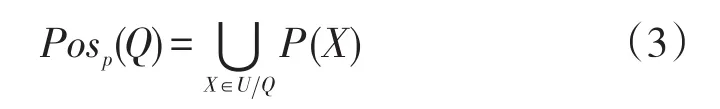
假定 P和 Q具有等价关系，R∈P，当POSind(P)(ind(Q))=POSind(p-{R})(ind(Q))时，则称R为P中Q不必要的；否则R为P中Q必要的。如果P中的每个R都为Q必要的，则称P为Q独立的。

设S∈P，S为P的Q约简当且仅当S是P的Q独立子族且POSind(S)(ind(Q))=POSind(p)(ind(Q)),P的Q约简称为相对约简。P中所有的Q必要的原始关系构成的集合称为P的Q核，记为coreQ(P)。

相对核与相对约简的关系如下：

coreQ(P)=⋂redQ(P)，其中redQ(P)是所有P的Q约简构成的集合。

为此，构建S=(U,A,V,F)为高校教师绩效考评指标信息集合，对于等价关系P⊆R有分类U ind(P)={X1,X2,…,Xn}，则P的信息量记为：

通过考察等价关系中蕴含的信息量，就能够确定在高校教师绩效考评指标体系中，哪个指标重要性高，哪个指标重要性低，哪个指标基本没有作用。在信息集合S=(U,A,V,F)中，指标属性a∈A在指标属性集A中的重要度和属性的信息量的关系可以确定为：

可以通过衡量去掉某个指标后信息系统信息量的变化情况来确定某项指标的重要程度。假如去掉某个指标后，信息系统的信息量具有显著的变化，说明该指标在整个信息系统中具有重要的作用，必须保留。反之就可以剔除。

因此通过式（6）

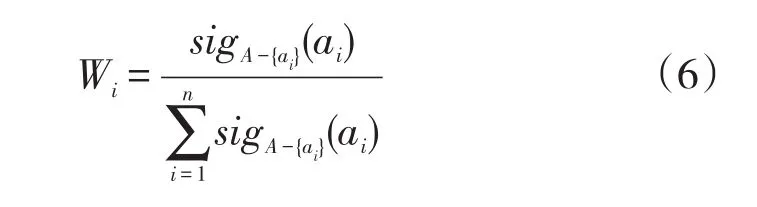
就可以计算出高校教师绩效考评指标体系中所有指标的权重。

然后通过式（7），设置合理阀值，依据偏离程度的量化，对指标进行约简。

Wi表示高校教师绩效考评指标体系中第i个指标的权重；Wmax表示所有高校教师绩效考评指标中权重最高的指标，Wmax-Wi表示高校教师绩效考评指标体系中第i个指标相对于Wmax指标的偏离程度，Wi数值越低，说明指标Wi与指标Wmax的偏离度越高。

依据实际情况和希望高校教师绩效考评指标体系的规模，确定科学合理的阀值，当Di的值超过确定的阀值时，说明指标i应当从高校教师绩效考评指标体系中删除。

3.2 基于SVM的绩效评价仿真

通过属性约简，得到最终的高校教师绩效考评指标体系，在此基础上，采用SVM算法对高校教师的绩效评价进行仿真。

把能够使式（8）中等号成立的样本称为支持向量（Support Vectors）。两类样本间间隙的大小可以定义如下：

寻找两类样本间最佳分类面的问题就可以转化为求函数式（10）

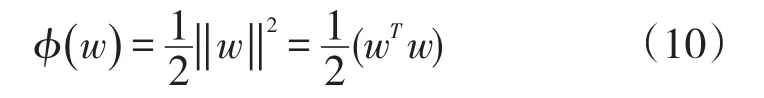
的最小值。

定义如下函数：

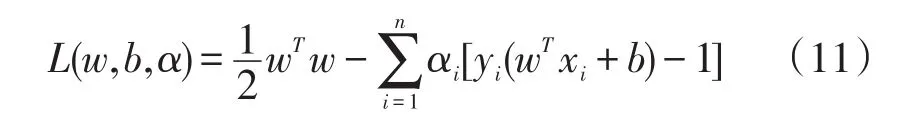
把式（11）分别对w、b、αi求偏微分并令它们等于0，然后加上原约束条件可以把原问题转化为如下凸二次规划的对偶问题。

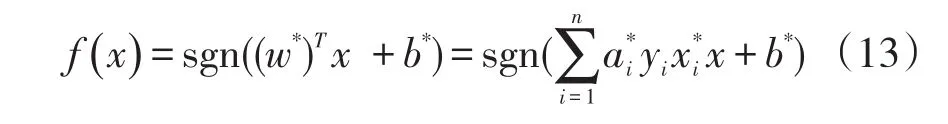
sgn()为符号函数。

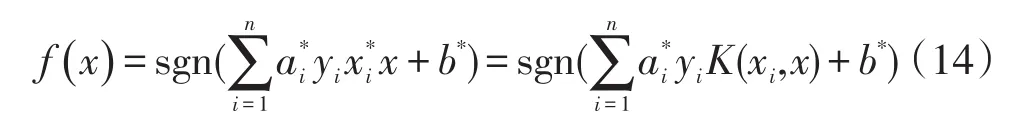
收集以往高校教师绩效考评的样本数据，将样本数据分为两组，每组都包含绩效考评成绩较好与绩效考评成绩较差的，将其中一组数据作为训练样本，采用Libsvm2.9工具箱，借助gnuplot工具进行参数优选，确定最终的SVM。将训练样本输入SVM进行训练，然后将测试样本输入模型进行测试，如未能达到预期的精度，再次对SVM进行训练，通过反复训练，得到满意的输出结果。

4 仿真证明

本文选取某高校物流专业近三年对所属教员绩效考评的243组数据作为样本数据。

首先，通过借助ROSETTA软件，将高校教师绩效评价22个指标中的连续型指标进行离散化处理，然后，利用这243个试验样本，通过RS模型对高校教师绩效评价指标体系进行约简，最终确定U13，U21，U24，U33，U43，U51，U61，U73八个指标为主要指标。

其次，选择合适的支持向量机核函数。核函数一般从以下几种函数中选取：（1）多项式核函数，即对应SVM是一个q阶多项式分类器。（2）径向基核函数，即对应SVM是一种径向基函数分类器。（3）S形核函数，则SVM实现的就是一个两层的感知器神经网络。

选用径向基核函数，将243组样本数据中前200组作为训练样本，后43组样本作为测试样本，条件属性为约简出的八个指标，使用Libsvm2.9工具箱中的gnuplot工具进行参数优选，结果如图1所示。

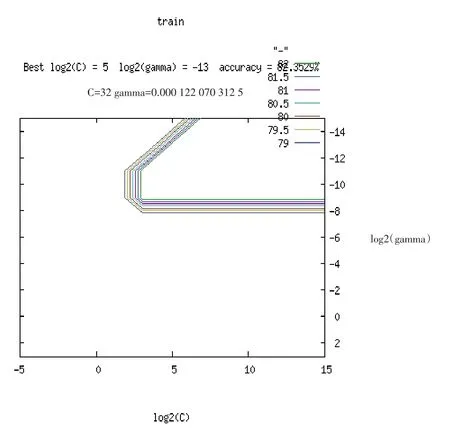
图1 支持向量机参数选取结果

将200个训练样本输入svm-train工具进行训练，将其余的43个样本输入svm-predict工具进行测试，通过实际输出的准确性发现，对43个测试样本的判别正确率达到98%。因此说明，本文建立的仿真模型具有较高的准确性。

5 结束语

本文构建了基于RS-SVM的高校教师绩效考评模型，该模型具有精度较高，操作简单，不受主观因素影响等特点，而且通过SVM的优势，在积累样本数据的基础上可以不断对模型进行训练，从而进一步提高模型的精度，可以为评估高校教师绩效水平提供科学的依据。