一种综合FAHP与目标规划法的装备备件调配方法

朱 臣，朱 倩，罗广旭

（空军勤务学院 航材四站系，江苏 徐州 221000）

1 引言

装备备件调配主要是指装备备件的补充和调整，它是以现有库存备件为基础，根据预定的决策目标，在考虑部队装备备件需求的基础上进行的决策活动[1]。科学合理的装备备件调配决策能够加快备件周转，而加快备件周转是降低库存规模的有效手段，目前，由于上级机关“统、调”职能作用发挥不够好，部分关键备件没有完全“转”起来，导致一些装备备件在一个单位出现积压呆滞，而在另一个单位却出现短缺的现象，为满足部队需求，这些单位只能增加储备量以维持保障能力，这样就导致了装备备件库存规模不断扩大，装备保障经济效益低下。

模糊层次分析法是一种将模糊数学与层次分析法相结合的方法，由于传统层次分析法受主体的主观想法、个人爱好影响比较大，所以会加大计算结果的误差，并且传统层次分析法在进行一致性检验时较为繁琐复杂，严格满足一致性要求较为困难，而模糊层次分析法求取各影响因素权重时，可以有效地避免传统层次分析法的弊端，更加科学、合理、有效和简洁。目标规划法节是在明确决策目标之后，依据该目标建立模型，通过求得决策目标与预计效果的最小差距，确定需要的最佳方案[2]。本文将通过将模糊层次分析法与目标规划法相结合，建立科学有效的定量决策方法，提高装备备件调配的科学性，为上级机关制定调配方案提供理论指导。

2 基于FAHP-GP的装备备件调配模型

2.1 模糊层次分析法

模糊理论是由美国控制论专家L.A.Zadeh在1965年创立的，用来处理传统精确数学无法解决的复杂问题。

2.1.1 基本原理。定义1：定义论域X，X到[0 ,1]闭区间的任一映射

都确定了一个模糊集A，μA͂是A的隶属度[3]。其中μA͂的取值代表了X对A的从属程度，μA͂值愈大，X从属于A的程度越高，μA͂的值愈小，X从属于A的程度越低。

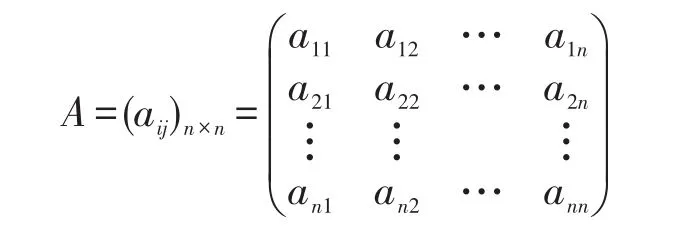
定义2：设矩阵A=(aij)n×n，若满足：

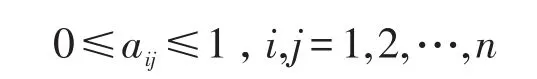
则A为模糊矩阵。

定义3：设矩阵A=(aij)n×n，若满足：

则模糊矩阵A又称为模糊互补矩阵。

定义4：若模糊矩阵A=(aij)n×n，满足：

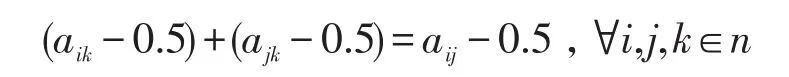
则A满足加性传递。

定义5：若模糊矩阵A=(aij)n×n，满足：

则A满足乘性传递[4]。

定义6：若模糊矩阵A=(aij)n×n，满足：

则模糊矩阵A是模糊一致矩阵，也是加性模糊一致矩阵。

模糊矩阵A中的元素aij表示第i个因素与第j个因素的相对重要程度[5]，其取值见表1。

表1 指标模糊评价标度表

2.1.2 计算步骤。（1）步骤一：建立层次结构模型。首先确定具有方案层、准则层和目标层的装备备件调配三层结构模型，该模型用来评价调配方案[6-7]。其中目标层是所需要的最佳装备备件调配方案；准则层是评判各个方案优劣的标准，本文选取部队装备实力、部队装备备件质量、结构优化作用、完成年度任务四个准则，这四个准则具体是指：

①部队装备实力：通过装备备件调配，对于部队装备实力提升的贡献作用。

②部队装备备件质量：在部队接收到调配备件后，对于装备备件质量的完善作用。

④完成年度任务：装备备件调配对于帮助年度任务完成的作用。

方案层是指具体的装备备件调配方案，即各个场站所调配的备件数量。

根据以上条件建立的层次结构模型如图1所示。

图1 装备备件调配层次结构模型

（2）步骤二：确定模糊一致评价矩阵。在层次结构建立之后，根据各领域专家对各备选方案打分，构建模糊一致评价矩阵。用S表示部队装备实力、Q表示部队装备备件质量、E表示结构优化作用、T表示完成年度任务，通过对准则层各元素进行比较，得相应的模糊一致评价矩A：

根据表1可得模糊评价矩阵C：

其中 cij为三角模糊数，cij=(lij,mij,uij)，lij、uij分别为模糊评价值的下限和上限，mij为模糊评价值，其值按照表1标度表进行选择。若C满足[8]：

1)从月际分布来看,6月暴雨雨日为全年最多,7月和8月次之,最少为1月和2月,无暴雨发生。梅雨和台风对临安的年降水量有巨大贡献,梅雨期间出现的暴雨雨日占暴雨总数的34.3%,而台风暴雨占到暴雨总数的21%。

①cii=0.5，i=1,2,…,n；

② cij=1-cji，i,j=1,2,…,n ；

③ cij=cik-cjk，i,j,k=1,2,…,n 。

则模糊判断矩阵C即为模糊一致评价矩阵A，若不满足，则需要继续对C进行调整，调整方法为对模糊评价矩阵C进行行求和及行变换：

调整到模糊评价矩阵C满足条件为止。对于有h个专家的情况，模糊评价值aij为：

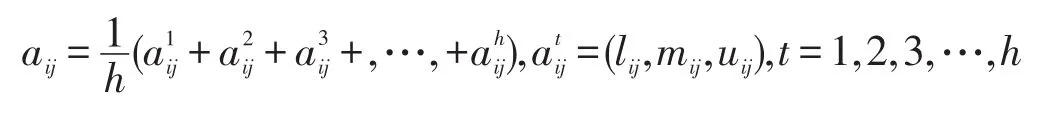
（3）步骤三：一致性检验与权重求解。依据模糊一致矩阵性质，模糊一致评价矩阵A必然符合一致性条件，不必再次一致性检验。

对矩阵C归一化处理，可得各准则在目标层的权重 w=（w1,w2,…,wn），其中：

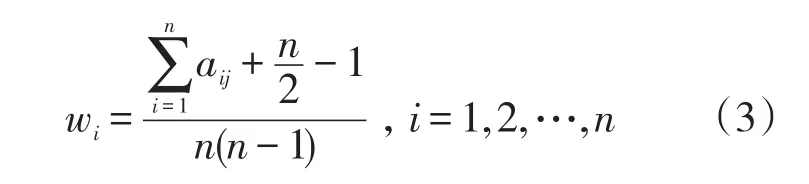
2.2 目标规划法

目标规划法是对层次结构模型中的方案层进行决策的一种方法，主要包括系统约束、准则约束和目标函数。

（1）系统约束。系统约束方程为：

上式中，需要调配的装备备件总数是C，部队i得到调配的装备备件数量是xi，单位向上申请装备备件数量时Ri，向上申请装备备件部队的总数是n。

上式中，部队i的装备备件消耗数量是ai；部队i补充前的装备备件数量是bi；为部队i补充前的一级品和二级品的装备备件总数是ci；部队i申请的装备备件数量是Ri。

（2）准则约束。准则约束方程为：

根据准则S、Q、E、T的最大化要求，考虑到准则层指标加权，得到偏差量加权的Z：

最优解就是使minZ成立的xi。

3 算例分析

加快备件周转是降低库存规模的有效手段，当前，由于上级机关“统、调”职能作用发挥不够好，部分关键备件没有“转”起来，因此为满足部队保障需求，只能增加储备量以维持保障能力。而装备备件调配模型能够为上级机关制定装备备件调配方案提供有力的决策支撑，下面以某型备件为例，说明FAHP-GP的装备备件调配模型的具体应用。

3.1 模糊层次分析法求解

已知全军该型装备备件当前库存数量C为13个，共有四个单位申请该型装备备件，各单位该型装备备件的库存情况见表2。根据各单位实际情况，按照准则层部队装备实力、部队装备备件质量、结构优化作用、完成年度任务四个准则，由三名相关领域专家对四个单位进行评分，得到相应的模糊评价矩阵C。

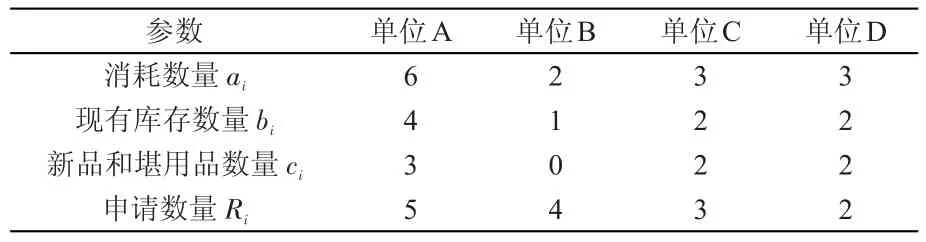
表2 各单位库存情况

模糊评价矩阵C为：

根据公式（1）和公式（2），将模糊评价矩阵C转化为模糊一致评价矩阵A：

根据公式（3）得到各准则在目标层的权重w：w=（w1,w2,w3,w4）=(0.258 3,0.241 7,0.275 0,0.225 0)

3.2 目标规划法求解

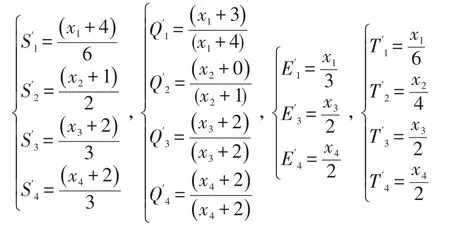
然后对其进行归一化处理得到Si、Qi、Ei、Ti的表达式：

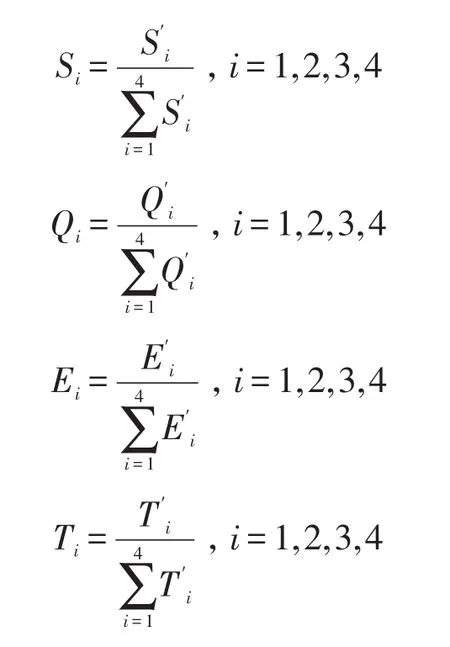
将Si、Qi、Ei、Ti的表达式带入公式（5），借助MATLAB软件，求出满足公式（6）的xi为：

所以，最终的调配方案为单位A分配6个，单位B分配3个，单位C分配2个，单位D分配2个，该调配方案是在充分考虑到各单位的实际，对于提高部队装备实力，完善部队装备备件质量，优化装备备件库存结构，推动年度飞行任务的完成具有理论指导意义，并且能够最大限度的发挥库存备件的作用，盘活现有库存，加快备件周转，提高装备保障的经济效益。

4 结语

军队系统内部对器材的占用数量直接影响器材保障费用和维护保管费用，要想使库存装备备件发挥其应有的作用，必须从提高备件周转率入手，盘活现有库存，防止库存积压，有效降低仓储费用和仓库管理开支，提高装备保障的经济效益。本文主要从装备备件调配入手，旨在加强上级机关装备备件调配力度，通过将模糊层次分析法与目标规划法结合起来，构建装备备件调配模型，改变以往的定性分析决策方式，运用定量分析手段解决备件供需矛盾，提高备件周转率，盘活现有库存，使库存装备备件充分发挥其应有的作用。