Fisher准则下的粒子群支持向量机在轴承故障诊断中的应用

,,,

(1.沈阳工业大学机械工程学院，辽宁 沈阳 110870；2.辽宁装备制造职业技术学院自控学院，辽宁 沈阳 110161；3.中认(沈阳)北方实验室有限公司，辽宁 沈阳 110164)

0 引言

滚动轴承是旋转机械最易发生故障的部件之一[1]。当滚动轴承出现故障时，不仅要识别故障的类型，还要量化损伤的程度，以便对故障轴承进行及时地修复和更换。

采集振动信号对滚动轴承运行状态进行分析是目前常用的故障诊断方法。由于振动信号具有非线性、非平稳性的特点[2]，传统的诊断方法往往需要凭借专业技术人员进行时域、频域或时- 频域分析，再给出诊断结果，这给专业知识相对薄弱的现场工作人员带来了难题。因此，近年来国内外学者致力于开发更简单、更方便的机器学习故障诊断方法。

支持向量机(SVM)是一种基于统计学理论的机器学习方法，它基于结构风险最小化原理，同时考虑了训练误差和分类器模型的容量，具有较好的预测精度，特别适合于小样本、非线性、高维度的情况[3]。

然而支持向量机(SVM)中惩罚参数和核函数的选取不同，会很大程度上影响分类精度，所以，一些学者应用智能搜索算法寻找支持向量机的最优参数。Samanta提出了粒子群算法结合人工神经网络的支持向量机在轴承故障诊断中的应用[4]，但该方法只优化了隐藏层节点；Yuan采用改进的离散粒子群算法进行特征选择[5]，但没有使选择的特征达到最优；Li利用改进的粒子群算法来优化SVM的参数[6]，但由于样本参数固定，存在收敛速度过慢的问题。

在粒子群算法中，适应度函数常用来评估每个粒子的性能，好坏的评价标准需要一个量化指标，为使特征子集的分类达到最大化，在此，提出了基于Fisher准则的粒子群支持向量机(FIPSO- SVM)故障诊断方法，尽可能减小类间重叠，加大分类间隔，提高分类精度，使其不仅用于确定故障的位置，还能量化故障的程度。

1 基本理论

1.1 SVM原理

SVM是一种基于统计学的机器学习方法，其基本模型定义为两类样本之间的最大间隔线性分类器，其学习策略为间隔最大化，而靠近边界的那些数据点则称之为支持向量[7]，一旦选定了支持向量就可以得到分类器的所有必要信息。

SVM通常设计成二分类器，设计的思路是寻找最优分类超平面wTx+b=0。从计算几何上理解超平面，最大化几何间隔等同于最小化‖w‖。因此，实际应用中分为2种情况，当样本集线性可分时，寻优问题表示为[8]：

(1)

当样本集线性不可分时，允许存在少量的离群点，但必须加以惩罚。因此，常引入松弛变量ξi>0和惩罚系数C，寻优问题成为凸二次规划问题，可表示为：

(2)

解决线性不可分问题的方法是向高维空间映射，设想有一种函数，它能接受低维空间的输入值，却能算出高维空间的内积值，这就是核函数。常用的核函数有线性核函数(Linear)、径向基核函数(Rbf)、神经元激活核函数(Sigmore)等。

引入核函数k(xi,xj)和拉格朗日乘子αi，则把式(2)写成对偶形式：

(3)

为使SVM的适用范围更广，当SVM处理多分类问题时，常将多类问题分解为一系列可直接求解的两类问题，在基于这一系列的SVM求解结果得出最终判断结果，有一对多(OAA)和一对一(OAO)等方法。

一对多方法是构造k个两类分类机，训练时第i个分类机取训练集中的第i类为正类，其余类别点为负类。判别时，取实际k个输出值的最大者对应类别为输入的类别。

一对一方法在每两类间训练一个分类器，因此，将有k(k-1)/2个分类函数。当对一个未知样本进行分类时，每个分类器都对其类别进行判断。决策时，采用投票法，最后得票最多的类别作为该位置样本的类别。

1.2 Fisher准则下改进粒子群优化方法(FIPSO)

粒子群寻优算法把每个问题解都看成一个粒子，所有粒子都由适应度函数(fitness function)去确定适应值以判断目前位置的好坏[9]。每个粒子必须赋予记忆功能，并能记住搜索到的最佳位置，每个粒子还有一个速度以决定搜索的步长和方向，这个位置和速度都可以动态调整和更新。

粒子i的速度更新公式：

(4)

粒子i的位置更新公式：

(5)

类内离散度矩阵公式为：

(6)

mi为第i类样本的均值。

总类内离散度矩阵公式为：

sw=s1+s2

(7)

类间离散度矩阵公式为：

sb=(m1-m2)(m1-m2)T

(8)

Fisher准则函数定义为：

(9)

使式(9)达到最大，则得到投影矢量的解为：

当sw是非奇异矩阵时，将对角矩阵λI(λ>0)加入到sw，因为sw是堆成半正定矩阵，则sw+λI是非奇异的，此时式(9)变为：

(10)

1.3 算法思路及流程

FIPSO- SVM故障诊断流程如图1所示。

图1 FIPSO- SVM故障诊断流程

由图1可知，针对采集的振动信号进行标准化处理，得到[-1,1]内的M×L维数据集，其中M表示信号数量，L表示特征数量。所谓的数据标准化就是消除变量之间的量纲关系，从而使数据具有可比性。

然后采用粒子群方法选择最优特征集，每个粒子中都包含位置和速度的信息，每个速度和位置的信息用二进制编码来表达，如某粒子向量x=[0 1 1 0 1 … 1]，向量元素为1时表示保留该特征，而向量元素为0时表示舍弃该特征，这样就会产生一个新的特征子集。

适应度的计算过程如下：

a.假设x中元素取1的总数为。

b.产生新子集的大小是M×K,1≤K≤L。

c.由式(7)和式(8)计算散点矩阵sb和sw。

d.用sb/(sw+λI)的特征向量估算投影矩阵w。

e.当sb，sw和w去定后，就可以得到式(10)的Fisher准则。

在接下来的粒子群算法中，每个粒子的适应值要与前一次迭代的适应值进行比较，得到当前粒子的局部最优解和种群的全局最优解，同时每个粒子的位置和速度信息也将得到更新，直至迭代终止。(迭代次数事先给定，并保证足够收敛到最优解)最后，根据FIPSO得到的最优解产生的最优子集将被分成2部分，一部分作为SVM的训练集，另一部分作为SVM的测试集。

2 FIPSO- SVM在轴承故障诊断中的应用

2.1 数据采集和特征提取

本文所采集的振动数据集来源于美国凯斯西储大学的轴承测试数据，数据种类分为正常、内圈磨损、外圈磨损、滚动体磨损等4种情况，磨损程度分为0.007英寸，0.014英寸，0.021英寸和0.028英寸，电机转速为1 797 r/min，信号的采样频率12 kHz，轴承型号为6205- 2RS深沟球轴承，其故障特征频率如表1所示。

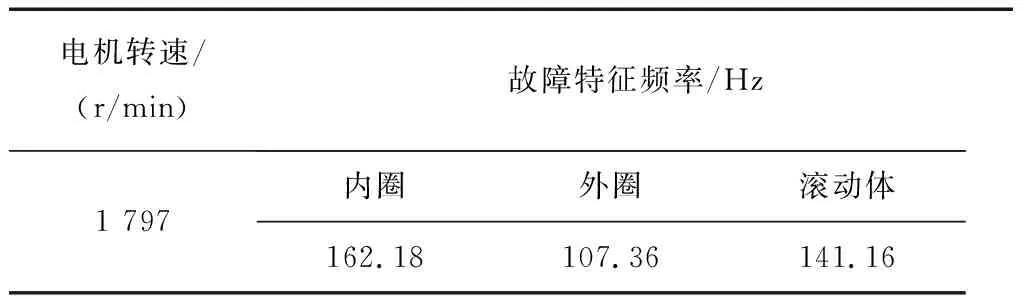
表1 滚动轴承各部件故障特征频率

为了增强故障识别能力必须提高故障信号的提取能力，振动信号提取的角度不同获得的信息也不同。

在时域分析上，主要通过信号的统计特征和概率分布来判别轴承故障。采用的时域指标有均值、峰值系数、峭度因子、偏度系数等[11]。

通过傅里叶变换，可以将时域信号转换为频域信号。频谱图描述了信号的频率与该频率信号幅值的关系，可以求得信号的频率成分和结构，进而分析系统的传递特征[12]。以常用的包络谱分析为例，该方法先得到结构的共振频率，然后使用带通滤波滤除干扰，显示弱脉冲分量，再使用Hilbert变换求出滤波信号的包络信号，最后对包络信号使用FFT变换求出包络谱，如图2所示。

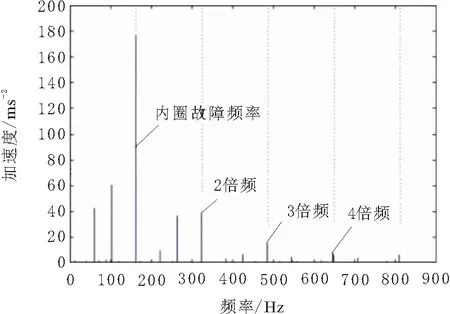
图2 内圈故障时的包络谱

2.2 全样本分类性能评估

通过时域和频域分析得到特征向量的样本数每种状态各32组，为了对比不同核函数对SVM分类器的影响，分别选择了线性核函数(Linear)、径向基核函数(Rbf)、神经元激活核函数(Sigmore)对全部32组特征向量进行了SVM训练，同时选用一对一(OAO)、一对多(OAA)2种不同算法进行计算。这里，准确率结果采用五折交叉验证的方法，表2和表3分别为全样本下的故障识别和故障等级的分类准确度。

表2 全样本下的故障识别 %

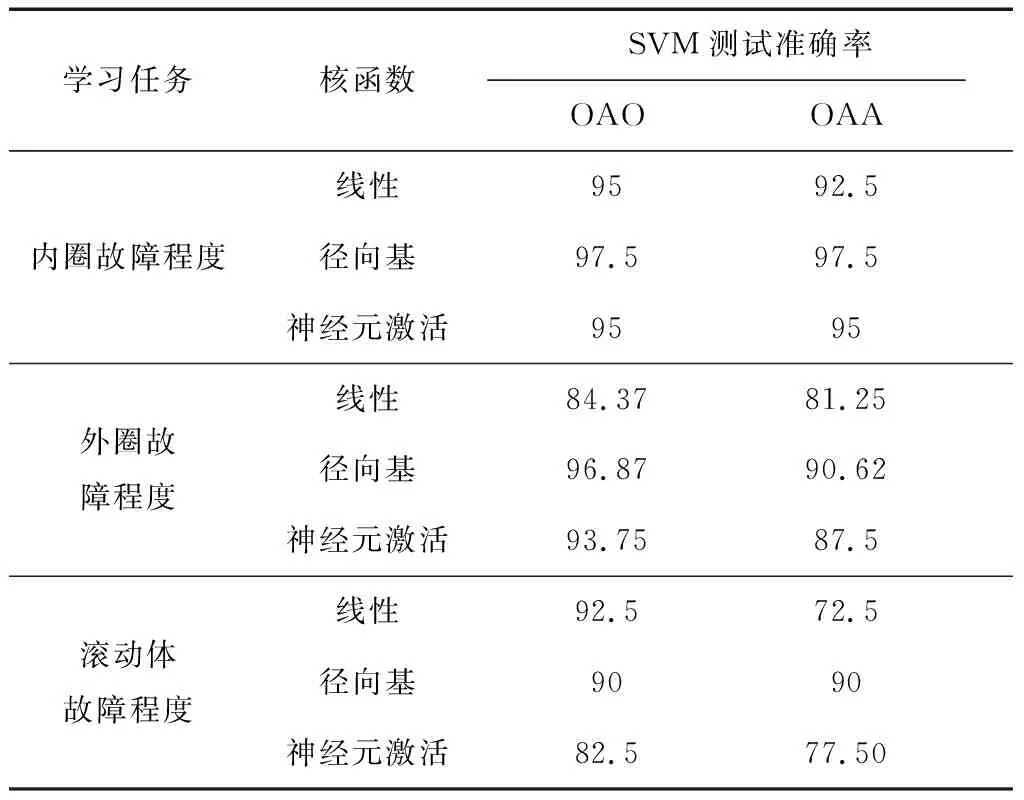
表3 全样本下的故障程度识别 %

2.3 FIPSO的收敛性

根据式(4)和式(5)，取ω∈[0.1,0.6]，v∈[-2,2]，c1=c2=2，可得到迭代结果如图3所示。

由图3可知，FIPSO算法在大约30次迭代后达到全局最优解，而标准粒子群算法的迭代次数大约在200次以上，这说明FIPSO算法可以显著调高收敛速度。

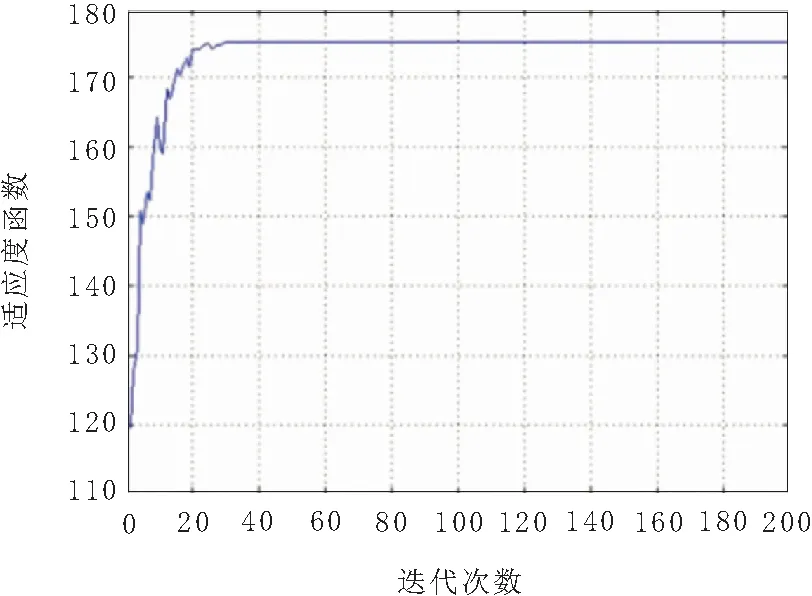
图3 FIPSO的迭代次数

2.4 测试结果比较

为进一步说明FIPSO算法的优越性，图4、图5、图6和图7表示不同工况下提取的故障频谱特征作主成分并绘制三维坐标散点图，从图中对比可以看出，采用最优特征子集的重叠率明显减少，说明分类效果比采用全样本更好。

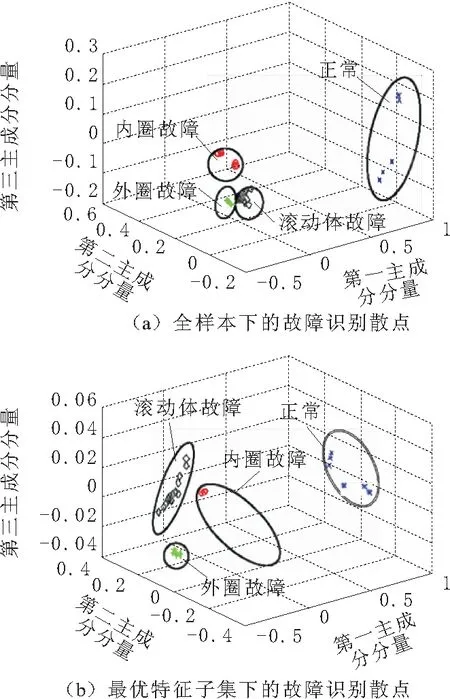
图4 故障识别散点图

表4和表5为最优特征子集下的故障识别和故障等的分类准确度。通过与表2和表3对比后，明显看出FIPSO- SVM具有更高的分类精度，并没有随输入训练样本数的减少而降低准确率。从算法上看，一对一(OAO)要优于一对多(OAA)。在3种核函数的分类对比中，径向基核函数的分类准确率稳定且明显高于其他2种，这说明径向基核函数具有良好的普适性。

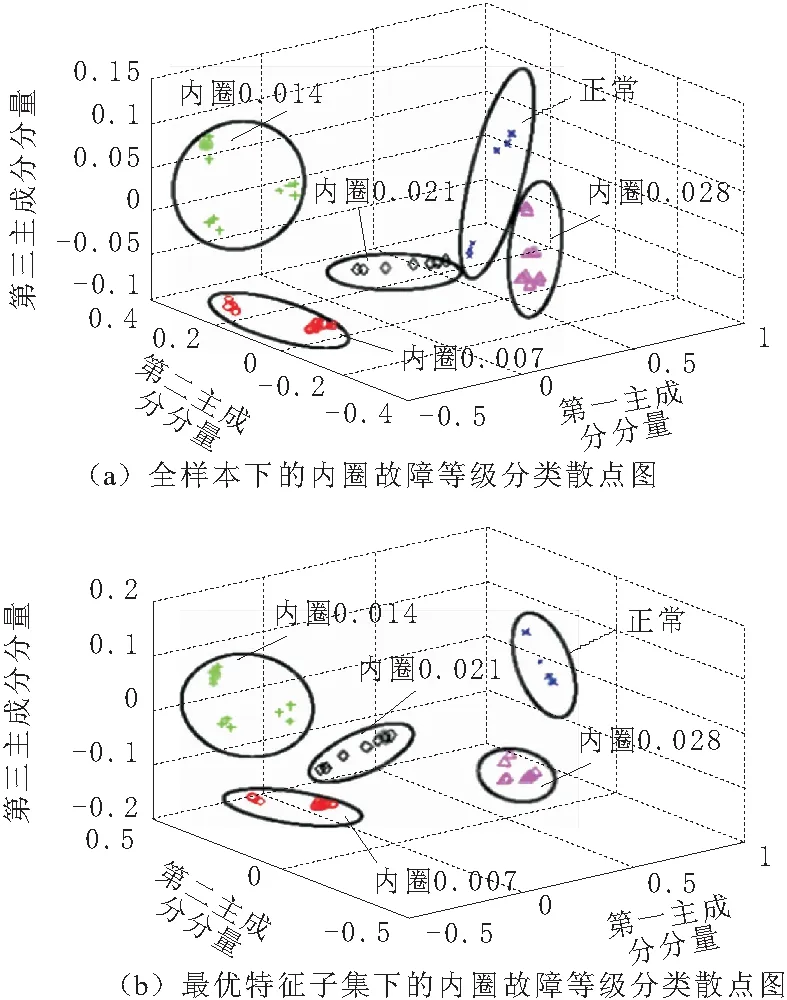
图5 内圈故障等级识别散点图

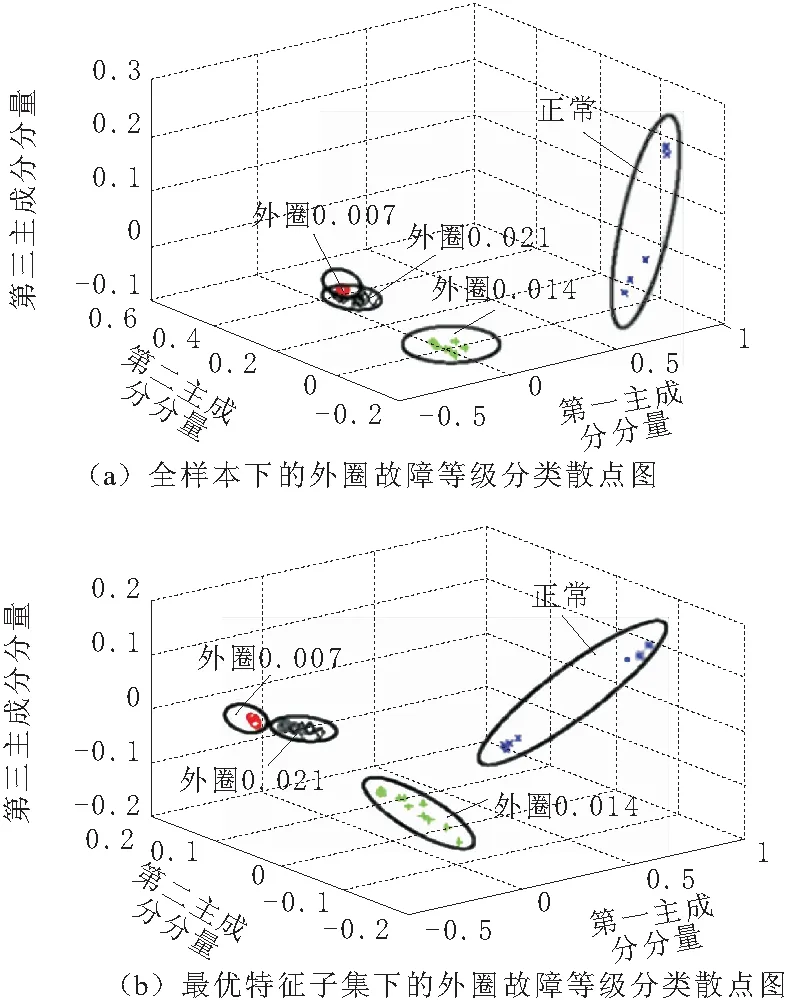
图6 外圈故障等级识别散点图

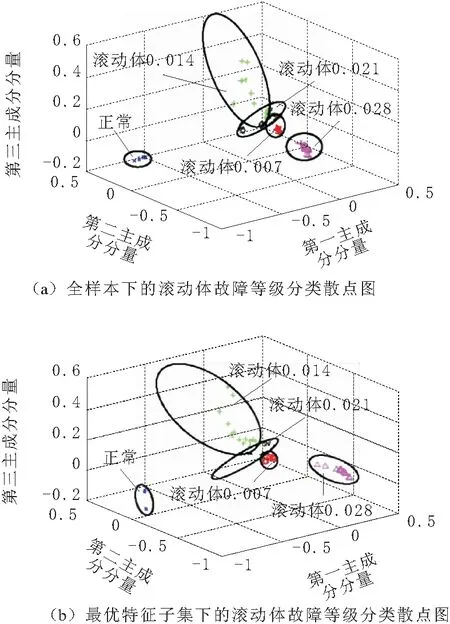
图7 内圈故障等级识别散点图

表5 最优特征子集下的故障程度识别

3 结束语

提出了Fisher准则下粒子群支持向量机(FIPSO- SVM)的故障诊断方法，即用Fisher准则得到的最优特征子集作为SVM分类器的输入，将滚动轴承4种状态下的振动数据进行时域和频率分析，提取32组特征向量，使用不同核函数和分类算法分别对全样本特征向量和最优特征向量子集进行故障识别和故障等级分类，以验证不同因素对SVM分类器的性能影响，并与基本粒子群的迭代次数进行比较。结果表明，FIPSO- SVM故障诊断方法可明显减小迭代次数。采用最优特征向量子集的方法进行SVM分类，并没有因为输入样本的减少而影响精度，而从整体比较来看，采用一对一分类算法要比一对多分类算法的准确率略高，径向基核函数在分类准确率上明显优于其他类型核函数。实验结果说明FIPSO- SVM具有收敛速度快、分类精度高的优点，值得在实际应用中进一步推广。