测地声模的扰动磁场与扰动磁矢分析

任海骏

(中国科学技术大学物理学院 合肥 230026)

1 引 言

测地声模是环形约束等离子体装置中特有的一种波动模式，具有环向对称(环向波数为零)和极向上近似对称的结构[1]。具体来说，极向扰动速度、径向电场和对应的扰动静电势具有极向波数为零的空间特征，而压强扰动和密度扰动在极向上则具有波数为 1 的正弦结构。测地声模的频率在离子声速的量级。

测地声模通常被认为是带状流的高频分支，对托卡马克等离子体中的边界湍流和等离子体输运有重要影响[2-4]，无论是理论分析[5-7]和数值模拟[8-10]，还是实验观测[11-13]均引起了等离子体物理学界广泛的关注与研究。实际上，测地声模通常不直接与湍流发生相互作用，而是通过影响径向电场，使径向电场作用于低频带状流，从而与湍流发生作用。

一般来说，对于低β量级等离子体(这里β定义为等离子体热压与磁压之比)，在磁流体力学框架下研究测地声模，通常利用如下两个假设：(1)动量方程中扰动磁场为零，同时扰动电流不为零；(2)扰动热压与磁压的合为零，以消除快磁声波的贡献。然后利用磁面积分极向动量方程，即可推导出测地声模的色散关系。2007年，中国科学院等离子体物理研究所的周登研究员利用漂移动理学方程研究了测地声模的磁场问题[14]，发现平行磁场方向极向波数为 2 的扰动回流产生了垂直方向波数为 2 的扰动磁场。2008年，Wahlberg[15]利用理想磁流体力学方程组研究测地声模本征模式的全局结构时，也在理论上预测了这种结构的磁分量存在。2009年，Wahlberg[16]进行了更为细致、深入的解析，获得了测地声模的径向和极向扰动磁场的表达式。西南物理研究所的 Wang 等[17]利用回旋动理学方程，解析推导了测地声模的扰动磁矢，并数值计算了有限β效应对测地声模频率和朗道阻尼的作用。Berk 等[18]的数值模拟结果表明，极向波数为 2 的扰动磁场分量占据主导地位，波数为 1 和3 的谐波分量在同一个量级，但远远小于波数为2 的分量。在理论研究和数值模拟之外，实验上也直接观测到了这样的磁场信号，如 JT-60U 托卡马克装置(日本)上的实验[19]和 TCV 托卡马克装置(瑞士)上的实验[20]，分别观测到了上述信号。

2014年，我们利用不同于文献[14,17]的方法，从理想磁流体力学方程组出发，分析测地声模的磁场扰动发现，平行方向的扰动磁场具有极向波数为 1 的结构，极向扰动磁场具有环向波数为 2的结构，并且两者具有相同的量级。径向扰动磁场则比极向扰动磁场还要小一个量级，并且具有波数为 2 的余弦结构[21]。但是，上述研究只考察了扰动磁场，并没有分析扰动磁矢，考虑到回旋动理学方程中处理的对象是扰动磁矢而不是扰动磁场，因此有必要分析清楚测地声模激发期间的扰动磁矢。本文研究正是基于此目的。

2 基本方程和线性化

效仿 Ren[21]的做法，我们定义扰动位移，并且按照如下方式展开：其中，是径向方向；是磁场方向单位矢量；下标分别表示径向、极向和平行方向的分量；同时定义同样，我们考虑大纵横比圆截面近似下的托卡马克位形，其中，R是托卡马克大半径；r是小半径。为了方便读者理解，我们稍微重复一下 Ren[21]的部分推导过程。由线性化理想磁流体力学方程组得到：

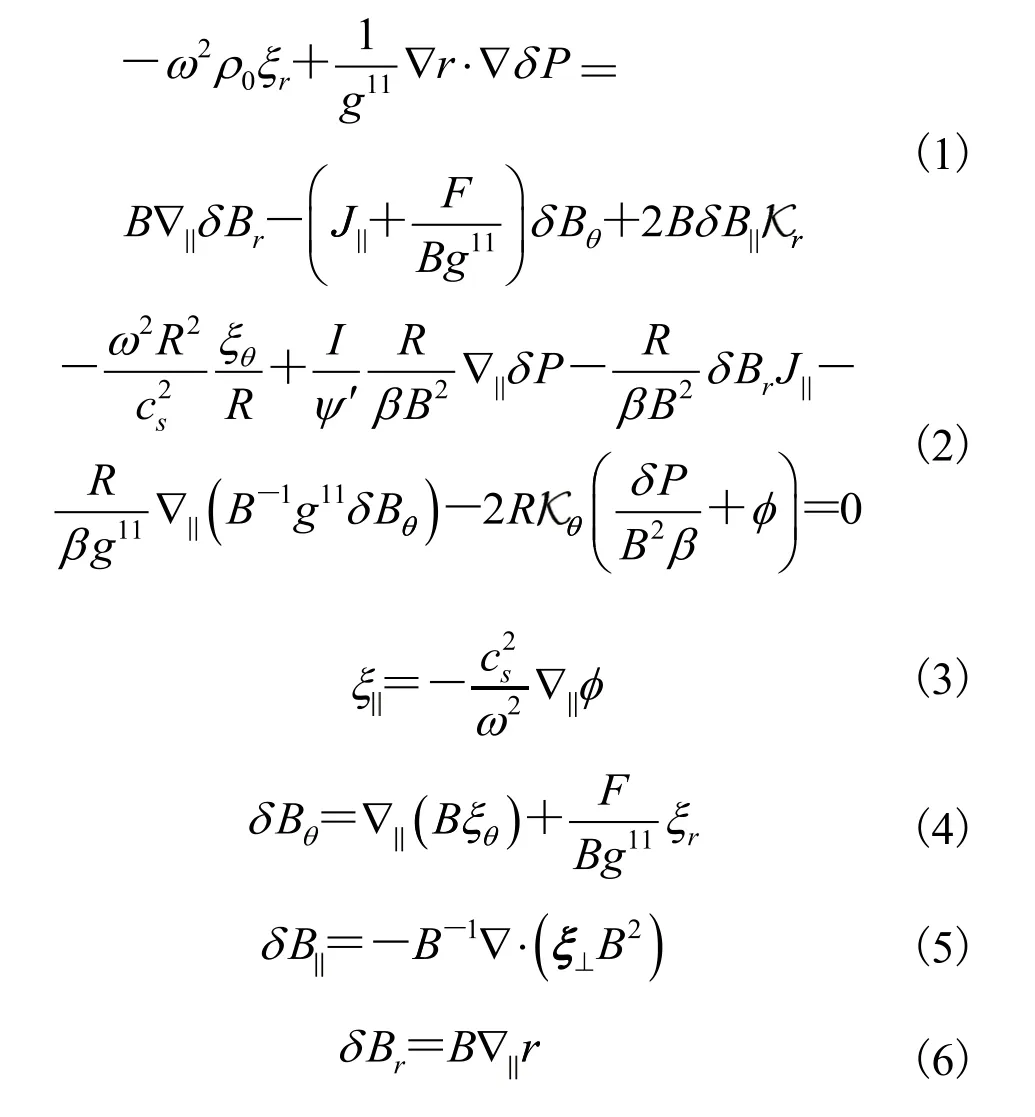
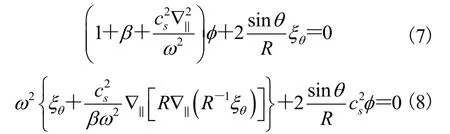
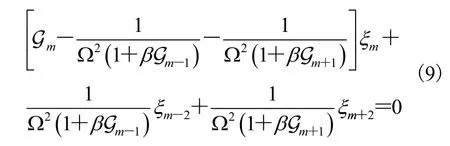
3 色散关系与扰动磁矢

基于公式(9)，在低β条件下，不考虑高次谐波的耦合效应，得到的测地声模主导量级的频率满足：

将上式代回到公式(4)和(5)中，可以得到如下的扰动磁场表达式：

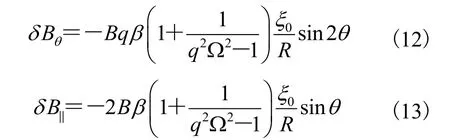
本文没有写出径向扰动磁场的表达式。这是因为，根据文献[21]可知，之前的分析中暂时丢掉了的影响，但如果要分析则必须要把找回来。下面，我们引入扰动磁矢在求解扰动磁矢的过程中会发现，径向扰动磁场可以很方便地求解出来，而不用寻找另外的假设。

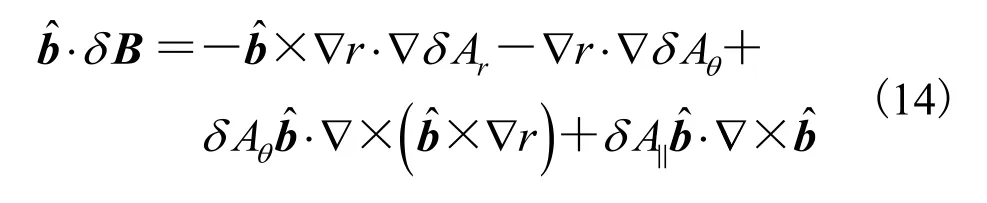
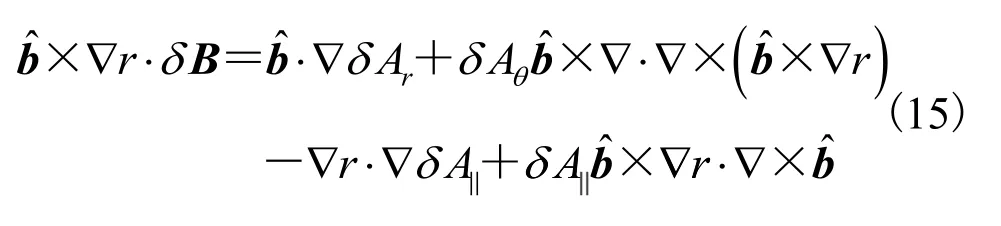
联立公式(12)～(15)，可以得到扰动磁矢极向和平行分量的表达式：

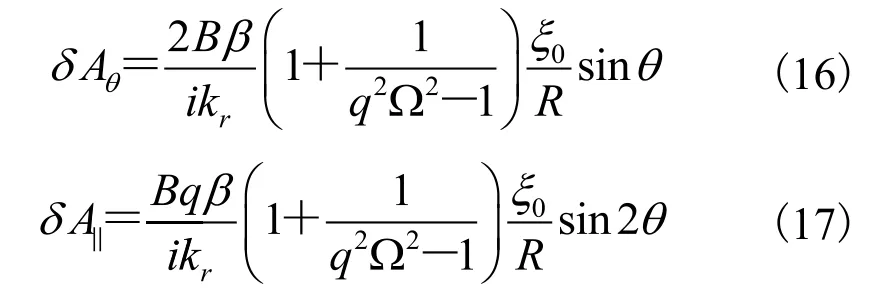
最后来看径向扰动磁矢。利用径向扰动磁场与扰动磁矢关系，有：

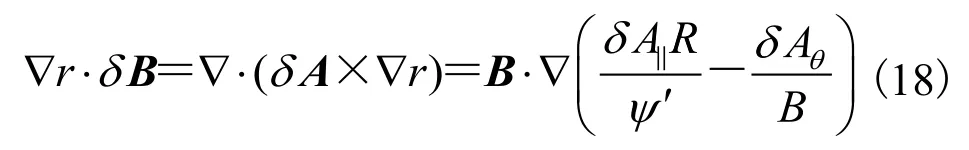
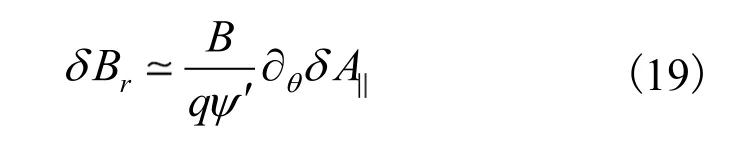
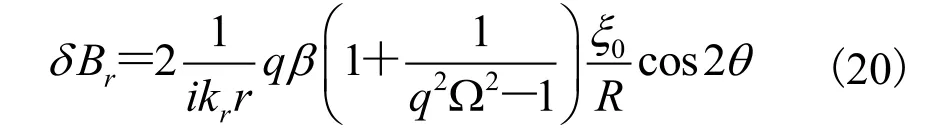
可以看到，公式(20)与文献[21]中的公式(19)完全一致，表明上述分析的准确性。

4 与国内外相似研究的对比分析

目前，测地声模的扰动磁场问题受到了较多关注，除了实验上对测地声模扰动磁场的观测外，很多理论研究者也从不同模型出发考虑过该问题。Zhou[14]从漂移动理学方程出发推导了扰动磁场信息，但没有明确分析扰动磁矢。Bashir等[22]从回旋动理学方程出发，研究了扰动磁矢对测地声模色散关系的作用，但计算中只考虑了扰动磁矢m＝1 的谐波分量。Sgalla[23]从双流体方程组出发，严格分析了扰动磁矢的影响，由于表达式过于复杂，不便与实验结果比对。2016年，Wahlberg 和 Graves[24]在理想磁流体力学框架下，深入、全面地分析了测地声模的全局模式、径向结构及扰动磁场问题，但没有考虑扰动磁矢。基于此，本文在磁流体力学框架下，对测地声模扰动磁场和扰动磁矢展开了理论研究。与上述国内外研究相比，可以发现：

(1)本文给出了扰动磁场和扰动磁矢简单明了的表达式，量级清晰，便于实验人员或数值模拟工作者直接利用本文的结果与相应的实验结果和数值模拟结果进行比对。

(2)相关推导过程立足理想磁流体力学方程组，图像清晰，数学复杂度不高，对等离子体物理相关的初级研究人员，特别是研究生来说，易于学习和理解，可以快速、准确地把握测地声模的物理图像和数学特征。

(3)同时注意到，理想磁流体力学方程组下的色散关系与动理学下的结果并不一致。已有研究表明，利用双流体方程或各向异性模型可以解决这一问题[25]，而本文暂时未考虑各向异性的问题。此外，Wahlberg 和 Graves[24]已经考虑到了非圆截面效应，本文只是局限于圆截面近似。这些是本文的不足之处，将在未来的工作中考虑进来。

5 总 结

本文利用理想的磁流体力学方程组，分析了大纵横比圆截面近似下托卡马克等离子体中的测地声模。推导过程中考虑了详细的磁场扰动信息，基于已有研究成果[21]，引入扰动磁矢，从而获得了平行方向与极向的扰动磁矢表达式。研究发现，平行方向的扰动磁矢与极向的扰动磁矢在一个量级上，径向扰动磁矢则远小于平行方向扰动磁矢。因为库仑规范的存在，扰动磁矢并不精确等于零，但可以直接忽略掉。

平行方向扰动磁矢(也即近似环向)具有极向波数等于 2 的正弦结构。换言之，在磁流体力学框架下，并不具有m＝±1 的谐波分量，或者说，m＝±1 的谐波分量并没有体现出来，对扰动磁场直接起作用的是m＝±2的谐波分量。这与回旋动理学框架下的结果不一致[17,22,23]，这种不一致也体现在扰动静电势上，反映了流体模型和动理学模型的差异。具体来说，在动理学中，无论是扰动电势还是扰动磁矢，各级谐波的量级都是按照是离子回旋半径)即有限拉莫半径逐渐递减的，如而在流体框架下，根据公式(11)，则有同时不难理解的是，理想磁流体力学框架下不存在有限拉莫半径效应，考虑到的量级近似，在流体图像和动理学图像下的结果是一致的。

与平行扰动磁矢不同的是，极向(垂直)扰动磁矢具有m＝1 的正弦结构。这一点也是回旋动理学方程无法给出来的，因为在动理学框架下，只保留了信息，这也是本文工作的意义所在。