某型飞机高原机场起飞滑跑距离的分析和计算

侯 照,邵 斌,王观虎,王建军,张宇晖

1.空军工程大学 机场建筑工程系,陕西 西安 710038

2.空军第四空防处工程处,陕西 宝鸡 721006

3.94162部队88分队,陕西 西安 710077

我国民航总局规定，一般高原机场是指海拔高度在1500 m～2438 m的机场，高高原机场是指海拔高度在2438 m及以上的机场[1]。与平原地区相比，高原地区环境复杂、气候恶劣，

在高原机场起降，飞机性能受到极大考验。飞机的起飞着陆性能因机场环境不同而呈现出较大差异，飞机起飞滑跑距离在高原地区和平原地区的差异更是十分明显[2,3]。相比起飞，飞机着陆时着陆滑跑距离主要受道面摩擦系数影响，发动机处于慢车状态，对着陆滑跑距离影响较小[4,5]，因此本文对着陆滑跑距离不做讨论，主要对起飞滑跑距离进行研究。

高原环境引起飞机起飞滑跑距离增长的因素众多，其中最主要的是高海拔空气密度减小导致的发动机推力减损和起飞离地速度增大。本文分析海拔升高对起飞滑跑距离的影响，拟合发动机推力曲面和气动系数曲线，以某型飞机在高原机场的起飞为研究对象，解析积分法计算起飞滑跑距离。

1 高原环境下起飞滑跑距离分析

1.1 起飞滑跑距离计算基本公式

常用的起飞滑跑距离计算方法包括公式法[6,7]，数值方法[8,9]，可靠性方法[10]，神经网络方法[11]，系统识别方法[12]等。数值方法计算起飞滑跑距离的求解方法包括数值积分法，解析积分法，微分方程组法和近似计算法。

本文采用数值方法计算起飞滑跑距离，将发动机推力、滑跑迎角、升力系数和阻力系数表示为速度的函数，确定起飞离地速度，积分计算起飞滑跑距离。

计算飞机起飞滑跑距离的一般积分表达式为[8]：

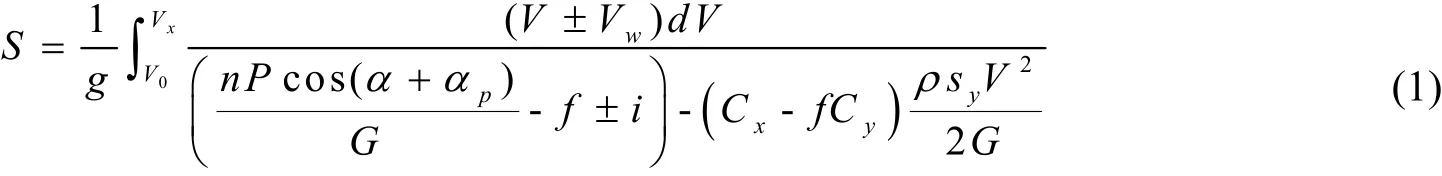
式中：S为起飞滑跑距离；g为重力加速度；V0为始端空速；Vx为末端空速；V为空速；Vw为滑跑方向的风速，逆风取负，顺风取正；n为发动机台数；P为单台发动机瞬时推力；α为滑跑迎角；αp为推力作用线与飞机机身轴线之间的夹角；f为机轮与地面的摩擦系数；i为跑道坡度，逆坡取负，顺坡取正；G=mg，为飞机的重量；Cx为空气阻力系数；Cy为升力系数sy为机翼面积；ρ为空气密度。

高原机场天气多变，多数情况下大气温度、压强和密度与机场海拔高度并不对应，因此需要调整计算公式使其符合高原实际大气条件。

1.2 高原环境起飞滑跑距离计算公式

在计算飞机高原起飞滑跑距离过程中，发动机厂商提供的发动机推力数据由海拔高度和马赫数确定，需要根据场道实际大气压强换算得到的压力高度作为计算发动机推力的压力高度，然后根据实际大气绝对温度计算音速，将滑跑速度转换为马赫数。最后根据压力高度和实际大气绝对温度计算得到实际空气密度。

由实际大气压强换算压力高度的公式为[9]：

高原机场非标准大气条件下的飞机起飞滑跑距离的积分表达式为：

式中：P(Hp,M)为由Hp和M确定的发动机瞬时推力；Hp为实际大气压强换算的机场压力高度；M为马赫数；psj为实际气压；ρsj为实际空气密度。

2 主要影响因素的计算

2.1 发动机推力曲面拟合

传统的发动机推力数值计算方法根据发动机性能曲线，查找不同海拔高度、马赫数处的推力值，采用拉格朗日二元三点插值得到未知点的发动机推力[5]。二元三点插值在某些特殊情况下可能会造成前后发动机推力不连续，导致计算失败或者造成较大误差，因此本文尝试采用其他插值和拟合方法确定发动机推力。

使用发动机厂商提供的发动机推力数据库的起飞状态推力数据，海拔高度每500 m为间隔，从1000 m到4500 m，马赫数每0.05为间隔，从0到0.45，形成的二元点处的发动机推力，作为发动机推力原始数据。目前建成并使用的高原机场海拔高度在1000 m到4500 m范围内，该型飞机起飞离地速度在马赫数0到0.45范围内，推力数据满足计算该型飞机高原机场起飞滑跑距离的要求。分别采用三阶插值和五阶拟合确定发动机推力关于压力高度和马赫数二元点处(Hp,M)的曲面，计算未知点发动机推力。

二元三点插值公式为：

式中：H1,H2,H3为距离Hp最近的三个高度值，M1,M2,M3为距离M最近的三个马赫数值。

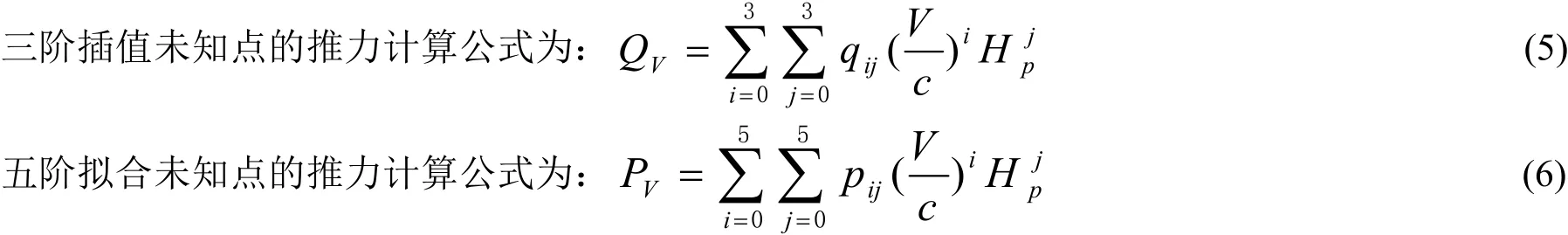
式中:QV为三阶插值的发动机推力，PV为五阶拟合的发动机推力；qij，pij为拟合系数；c为实际气压、气温计算的音速；

为检验计算的准确性和对比计算误差，选取海拔2000 m、4000 m处，马赫数值分别为0，0.1，0.2，0.3，0.4的发动机推力为未知点进行检验和对比，计算结果和误差如表1所示。

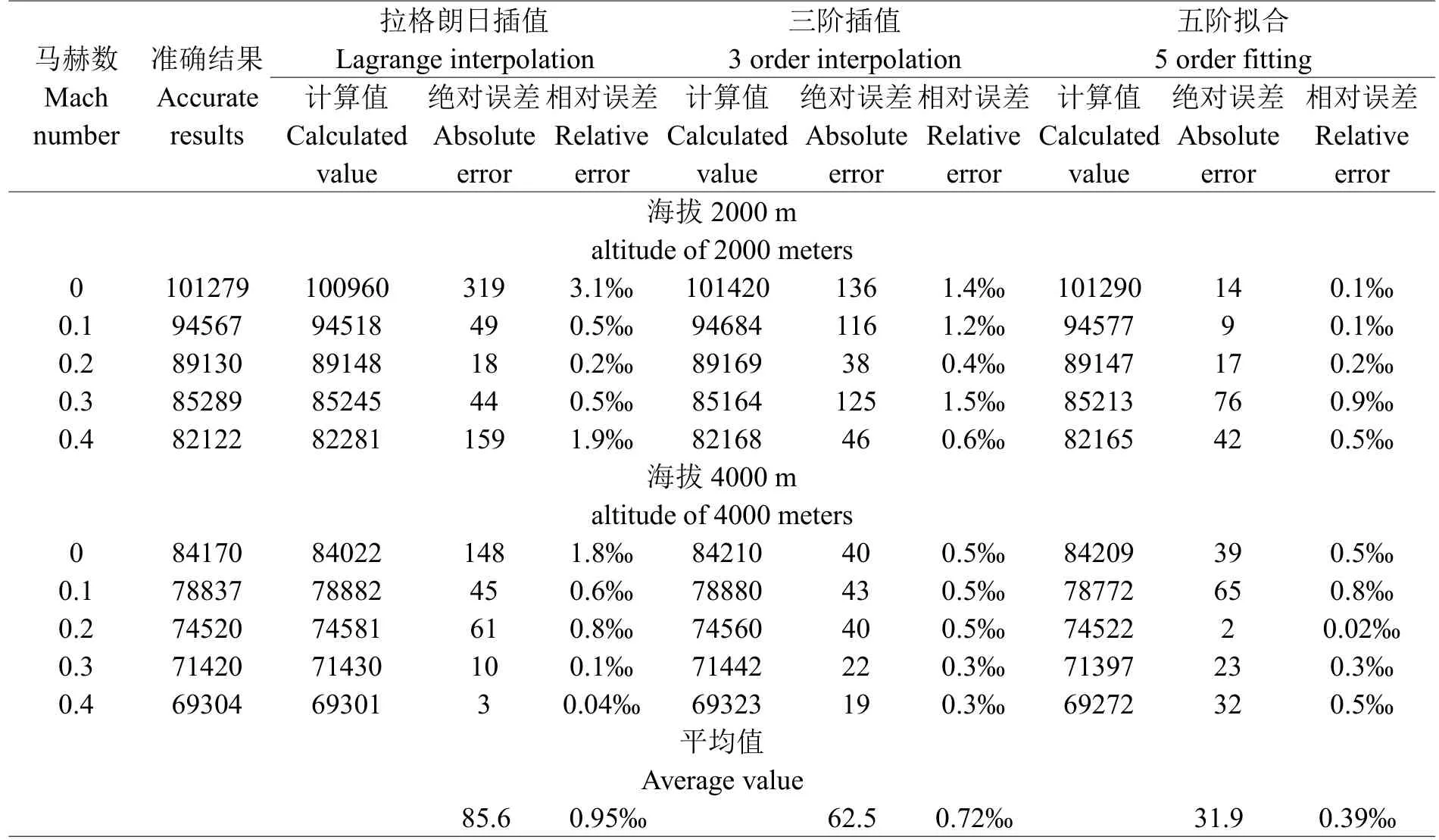
表1 海拔高度2000 m、4000 m处瞬时发动机推力的计算结果Table 1 Calculation result of instantaneous engine power at altitude of 2000 and 4000 meters

从表1中看出二元三点插值、三阶插值、五阶拟合确定的未知点推力的绝对误差分别为85.6、62.5、31.9，相对误差分别为0.95‰、0.72‰、0.39‰。五阶拟合确定未知点推力的精度更高，有利于高原机场起飞滑跑距离计算，在计算起飞滑跑距离过程中，发动机推力按照五阶拟合计算确定。

2.2 升阻力系数曲线拟合

传统的起飞滑跑距离计算过程中，将两轮滑跑阶段飞机滑跑迎角等同于离地迎角进行处理。高原环境下发动机推力减损，升阻力在飞机所受合力中的占比相对增大；同时起飞滑跑距离大幅度增加，飞机两轮滑跑距离也相应增加，升阻力对滑跑距离的影响增大。为计算准确，本文将升阻力系数表示为速度的函数。

首先建立滑跑迎角和速度的对应关系，飞机在起飞过程中，飞机迎角从抬前轮开始到空中爬升期间连续增大，同时，飞行手册中要求飞行员缓慢线性拉杆，因此可以认为在滑跑过程中，飞机迎角在三轮滑跑和抬前轮瞬间为停机角，在抬前轮后和离地前线性增加，直到增大为离地迎角。建立迎角和速度之间的分段函数为：

式中：α为滑跑迎角；V为滑跑速度；αij为停机迎角；αld为离地迎角；Vq为起飞离地速度；Vr为抬前轮速度，一般认为等于0.8Vq[13]。

根据飞机的升力系数与阻力系数随迎角变化关系，如表2所示，采用二阶多项式拟合方法，确定升力系数、阻力系数和迎角之间的函数关系。

表2 升力系数与阻力系数随迎角变化关系Table 2 The relationship between the lift and resistance coefficient with the angle of attack

得到升力系数、阻力系数和迎角之间的拟合多项式为：

式中：Cy为升力系数；Cx为阻力系数。

将迎角和速度之间的分段函数代入升阻力系数和迎角之间的拟合公式，即将公式（7）代入（8）、（9）得到升阻力系数随速度变化的二次函数关系式。

2.3 起飞离地速度

起飞离地速度是飞机离开地面的速度，与空气升力和飞机重量有关，在飞机离地瞬间，忽略发动机竖向的分力，飞机受到的升力和重力相等，高原机场实际大气条件与标准大气条件不同，起飞离地速度的计算公式如下所示。

式中：Δ为空气相对密度；Vq0为标准大气条件下的离地空速；mq0为Vq0对应的起飞质量；mq为实际起飞质量；tsj为实际气温。

为了分析起飞重量和海拔高度对起飞离地速度的影响，分别统计海拔高度接近0 m、1000 m、2000 m、3000 m、4000 m的机场气象数据，根据机场的最热月平均温度和平均气压，计算飞机在不同海拔高度下以不同起飞质量起飞的相对空气的离地速度，如图1所示。

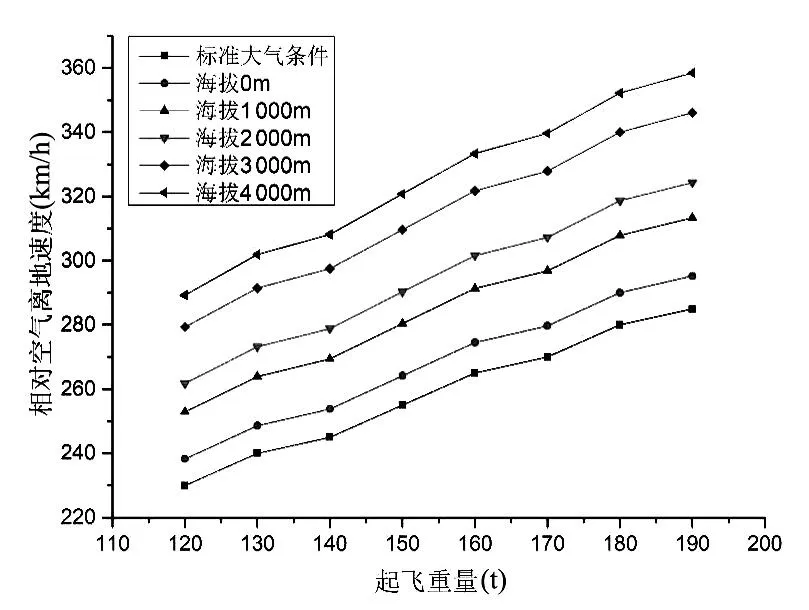
图1 离地速度和起飞重量、海拔高度之间的关系Fig.1 The relationship between the take-off speed with the take-off weight and altitude

从图1中可以看出，由公式（10）、（11）确定的起飞离地速度随起飞重量和海拔高度的增加而增大，同时可以看出，在不同海拔高度下，起飞离地速度随起飞重量的变化趋势是一致的，在同一起飞重量下，随着海拔升高，相同海拔高度增量对应的起飞离地速度增量逐渐增大。

3 解析积分法计算起飞滑跑距离

高原机场飞机起飞离地的过程和平原机场相同，都要经历静止全加力、三轮滑跑、抬前轮滑跑三个阶段，直到离地起飞，因此高原起飞滑跑距离计算模型与平原相同。根据飞机起飞时的大气条件，计算得到压力高度，进而将推力和升阻系数表示为速度的函数，由于其它参数在滑跑过程中基本保持不变，因此在滑跑过程中均作常数处理。

根据飞机性能手册上标准大气条件下的起飞离地速度和标准起飞离地质量，通过公式（10）、（11）换算得到实际起飞离地速度。将推力和升阻力系数关于速度的多项式代入起飞滑跑距离计算公式，分别得到三轮、抬前轮滑跑距离计算公式，如下所示。

三轮滑跑阶段的滑跑距离计算公式为：

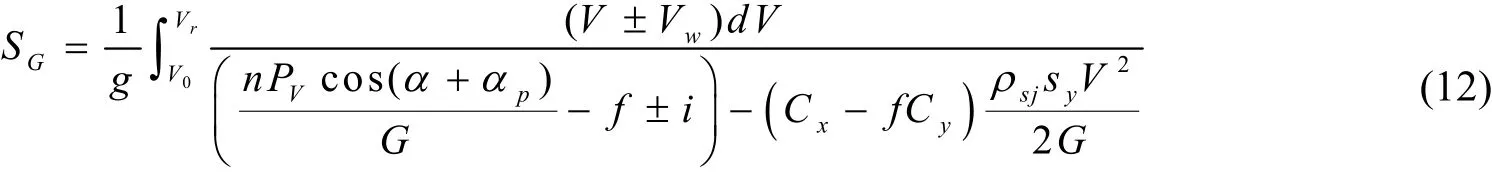
三轮滑跑阶段α为定值，取αtj；V0=0。

抬前轮滑跑阶段的滑跑距离计算公式为：

抬前轮滑跑阶段α为变化值，在αtj～αld间变化，k为荷载分散系数，一般取飞机总重量的90%～95%分配在主起落架上。

式中：Sq为总起飞滑跑距离；SG为三轮滑跑距离；SR为抬前轮滑跑距离。

4 计算验证

分析某型飞机在海拔高度2000 m、3000 m和4000 m的机场起飞滑跑距离，以某型飞机的实际起飞滑跑距离数据插值结果作为实际值，根据滑跑距离计算图表和本文计算方法计算起飞滑跑距离，考虑飞行员驾驶操纵误差系数为1.15修正计算的起飞滑跑距离[14]，绝对误差为计算修正值和实际值之差，对比实际值、查图表法和本文解析积分求解方法的计算结果，验证拟合系数和计算方法的正确性。部分计算参数、实际起飞滑跑距离插值、查图和计算的起飞滑跑距离计算结果如表3所示。

表3 实际起飞滑跑距离和计算起飞滑跑距离Table 3 The actual takeoff distance and takeoff distance calculation

由表3可知，计算值与查图值相近，差值绝对值的平均值为15 m。计算修正值与实际值相近，绝对误差绝对值的平均值为14 m，相对误差绝对值的平均值为0.5%，验证了本文拟合系数和计算方法的正确性。由计算值和实际值计算得到的驾驶误差系数为1.156，接近1.15，说明本文拟合系数和计算方法正确。

5 讨 论

本文计算的起飞滑跑距离误差与前人研究计算的起飞滑跑距离误差结果相近，验证了本文计算思路和计算方法的正确性，能够为某型飞机高原机场的跑道长度设计计算提供理论参考。本文只分析了飞机在正常起飞时的滑跑距离，未考虑一发失效情况下飞机中断起飞或继续起飞的滑跑距离，对此方面的内容有待进一步深入研究。

6 结 论

本文建立发动机推力和升阻力系数关于速度的拟合公式，发动推力采用五阶拟合，建立升阻力系数和速度的函数关系，较准确地反映了发动机推力和升阻力系数随速度的变化。采用解析积分法计算起飞滑跑距离，对比插值法、查图表法和本文方法的计算结果，本文方法的绝对误差绝对值的平均值为14 m，相对误差绝对值的平均值为0.5%，验证了本文拟合系数和计算方法的正确性。