轿车底盘橡胶衬套半经验设计方法研究

邓雄志 刘涛 苏泽博

（广州汽车集团股份有限公司汽车工程研究院，广州 511434）

主题词：轿车底盘 橡胶衬套 各向刚度 半经验设计

1 前言

汽车底盘橡胶衬套的各向刚度直接决定底盘的操纵稳定性、平顺性、NVH性能及承载变形性能[1-2]等，因此，整车制造厂及其研发机构对底盘各衬套刚度目标的设定关注度较高，而对衬套结构设计关注较少[3-4]。

目前国内橡胶衬套生产商对衬套的结构设计依然处于借鉴和沿用的状态[5-6]，生产商具有自己的产品刚度数据库和对标刚度数据库，根据衬套的设计空间和主机厂的刚度目标要求从数据库中进行衬套选型，经过微调结构和胶料硬度、配方达到刚度目标。这种借鉴和沿用的方法非常依赖工程经验，且一般很难保证各向刚度全部与目标吻合，操作性及知识延续性差[7]。为此，本文通过仿真方法重点研究衬套结构参数与衬套橡胶的各向刚度关系，提出了橡胶衬套半经验优化设计方法。

2 衬套结构参数与刚度关系研究模型

为研究衬套结构参数与衬套各向刚度的关系，从最简单的两骨架衬套[8]（图1）入手，在保持材料参数及其它结构参数不变的情况下，分别研究内径变化、外径变化、轴向长度变化及内外径同时变化（保持橡胶厚度不变）时对衬套各向刚度的影响，明确刚度与衬套结构尺寸变化的关系，以设计出满足刚度目标的衬套。

图1 两骨架衬套结构示意

图2为某轿车悬架衬套的原始尺寸，橡胶层初始内径为24 mm，外径为40 mm，轴向长度为37 mm，以该衬套为原型研究衬套结构尺寸变化与各向刚度的关系。

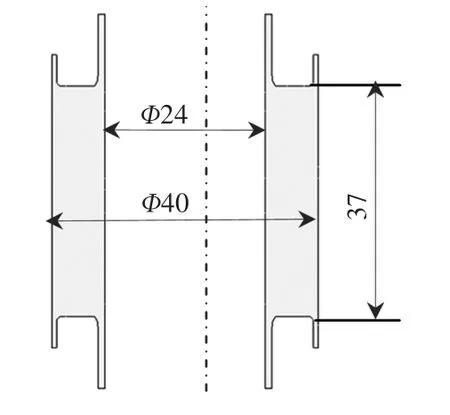
图2 衬套的原始尺寸示意

采用C3D8H单元建立有限元模型，原始衬套的节点数为42 300，单元数为34 000，如图3所示。橡胶材料本构采用Mooney-Rivlin模型[9-10]，系数C10为0.297、C01为0.058，用该有限元模型计算衬套各向刚度，然后调整衬套尺寸，重新划分网格，计算尺寸变化后的各向刚度。

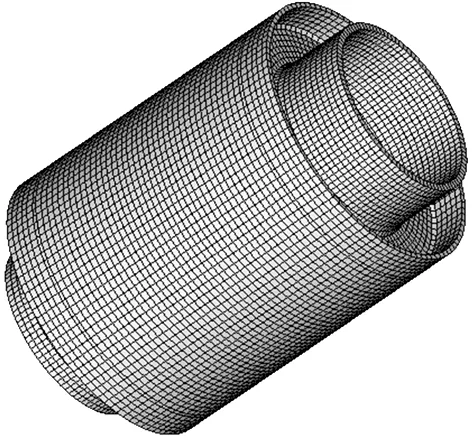
图3 衬套刚度分析有限元模型

为研究各向刚度相对内径变化的敏感程度，将刚度变化率相对尺寸变化率的比值定义为刚度相对变化率，表达式为：

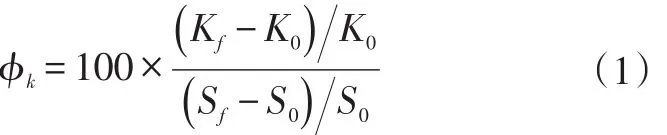
式中，φk为刚度相对变化率；Kf为衬套结构尺寸变化后的衬套刚度；K0为初始衬套刚度；Sf为变化后的衬套结构尺寸；S0为初始尺寸。

式（1）中分子为刚度变化率，分母为尺寸变化率。φk=1表示刚度变化率与尺寸变化率相等，即尺寸变化1%，则刚度同时变化1%，φk值为负则表示刚度与尺寸的变化呈反向变化趋势。

记刚度变化率α为，尺寸变化率β为，则式（1）变化为：

3 衬套结构参数对各向刚度的影响

3.1 内径变化对衬套刚度的影响

3.1.1 不同内径的衬套刚度分析

保持衬套外径及轴向长度不变，将内径分别设置为24±2 mm和24±4 mm，计算内径变化后衬套各向刚度，结果如表1所列。

各向刚度与内径关系曲线如图4所示，由图4可知，各向刚度随内径的增大逐渐增大，随内径减小而减小，且呈现出非线性趋势；内径增大时，各向刚度变化幅度较大，其中，径向刚度及摆动刚度的变化幅度最大，呈指数增长趋势；内径减小时变化幅度相对较小。

图4 各向刚度与内径关系曲线

3.2.2 内径变化量与各向刚度关系

根据式（1）计算各向刚度相对变化率，结果如表2所列，刚度相对变化率与内径变化量关系曲线如图5所示。

表2 内径变化量对应的刚度相对变化率

由图5可知，刚度变化率均为正，各向刚度与内径的变化成非线性正比关系；径向刚度相对变化率最大，均在300%以上，摆动刚度相对变化率其次，轴向刚度相对变化率最小，即径向刚度对内径的变化最敏感，轴向刚度对内径变化敏感度最低；内径增大与内径减小相比，内径增大时刚度相对变化率更大。

图5 刚度相对变化率与内径变化量关系曲线

3.2 外径变化对衬套刚度的影响

保持内径24 mm及轴向长度37 mm不变，外径从40 mm分别增加和减少2 mm和4 mm，计算外径变化后衬套各向刚度，再根据式（1）计算各向刚度相对变化率，结果如表3所列，刚度相对变化率与外径变化量的关系如图6所示。

表3 外径变化量对应的刚度相对变化率

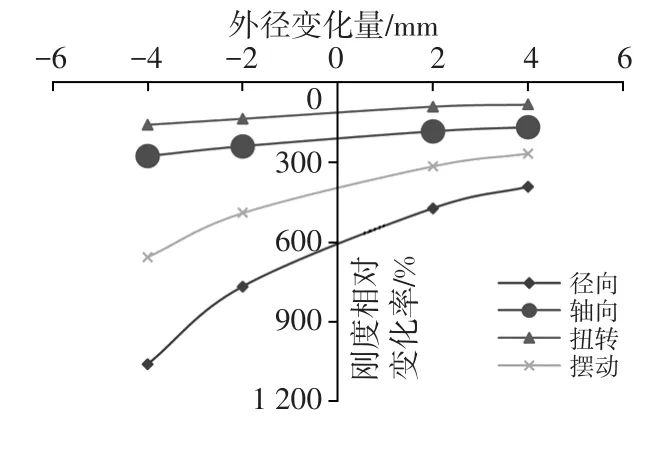
图6 刚度相对变化率与外径变化量曲线

由图6可知，各向刚度相对变化率为负值，各向刚度与外径的变化量呈非线性反比关系；径向刚度的相对变化率较大，均在400%以上；扭转刚度相对变化率最小，只有约100%；外径朝半径方向减小时各向刚度的变化更明显。

3.3 轴向长度变化对衬套刚度的影响

保持内径24 mm及外径40 mm不变，轴向长度分别增大和减小3 mm、6 mm，使轴向长度分别变为31 mm、34 mm、37 mm、40 mm和43 mm，计算轴向长度变化后衬套各向刚度及刚度相对变化率，结果如表4所列，刚度相对变化率与轴向长度变化量的关系曲线如图7所示。

由图7可知，刚度相对变化率为正，各向刚度与轴向长度呈正向非线性比例关系；摆动刚度的相对变化率最大，相对轴向长度的变化最敏感，径向刚度其次；轴向及扭转刚度变化率接近100%，说明轴向及扭转刚度的变化率与轴向长度的变化率几乎是1∶1的关系；轴向长度正向或负向变化对径向刚度、轴向刚度、扭转刚度的影响几乎趋势一致，相对于轴向长度减小，轴向长度增大对摆动刚度的影响更大。

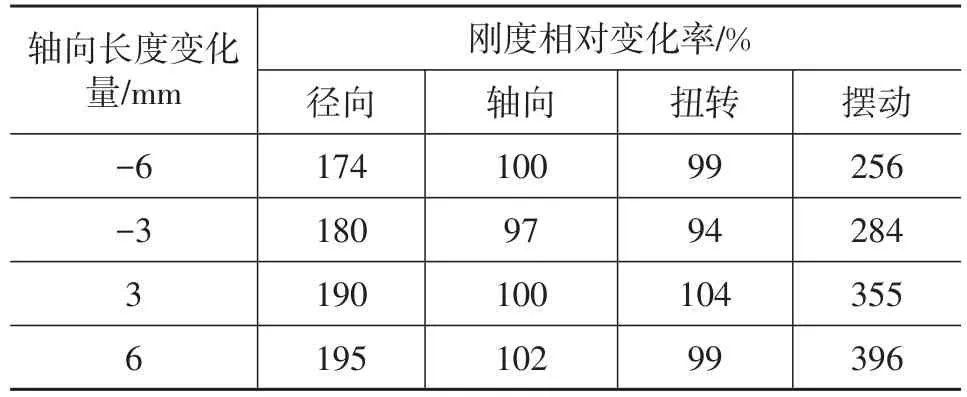
表4 轴向长度变化量对应的刚度相对变化率

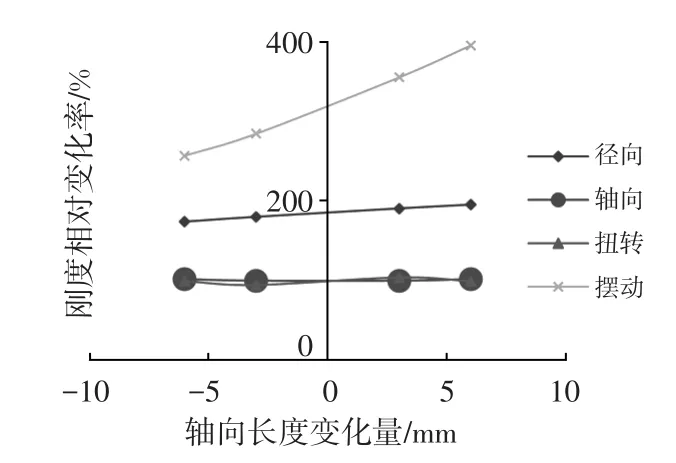
图7 刚度相对变化率与轴向长度变化量曲线

3.4 内外径同步变化对衬套刚度的影响

保持橡胶径向厚度和橡胶长度不变，内、外径同步增大和减小2 mm、4 mm，使衬套沿半径方向整体同步增大或减小，调整后共有5个衬套，其内、外径分别为20 mm和36 mm、22 mm和38 mm、24 mm和40 mm、26 mm和42 mm、28 mm和44 mm，计算5种不同内、外径的衬套各向刚度，再根据式（1）计算各向刚度相对变化率，结果如表5所列，刚度相对变化率与内、外径变化量的关系曲线如图8所示。

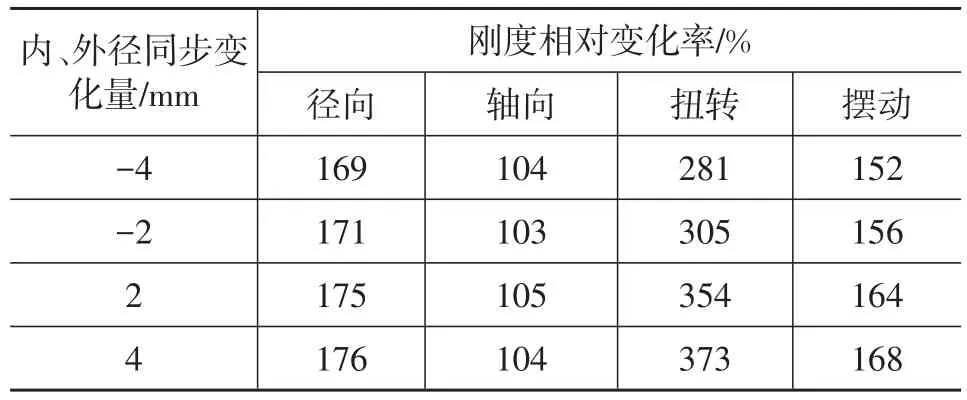
表5 内、外径同步变化量对应的刚度相对变化率

由图8可知，刚度相对变化率为正，说明各向刚度与内、外径的同步变化量呈正向比例关系；扭转刚度相对变化率最大，其对内、外径同步变化最敏感；轴向刚度的相对变化率最小，接近100%，径向刚度、摆动刚度的相对变化率居中，都在200%以下；径向、轴向、摆动刚度相对变化率曲线基本保持水平，内、外径同步增大或减小时，对径向、轴向、摆动刚度的影响一致，内、外径同步增大时则对扭转刚度的影响更大。

图8 刚度相对变化率与内、外径同步变化量曲线

前述分析表明，内、外径的变化对径向刚度的影响最大，对摆动刚度的影响其次，对轴向刚度及扭转刚度的影响较弱；轴向长度变化对摆动刚度的影响最大；内、外径同步变化对扭转刚度的影响最大，对轴向刚度的影响较弱，如表6所列。

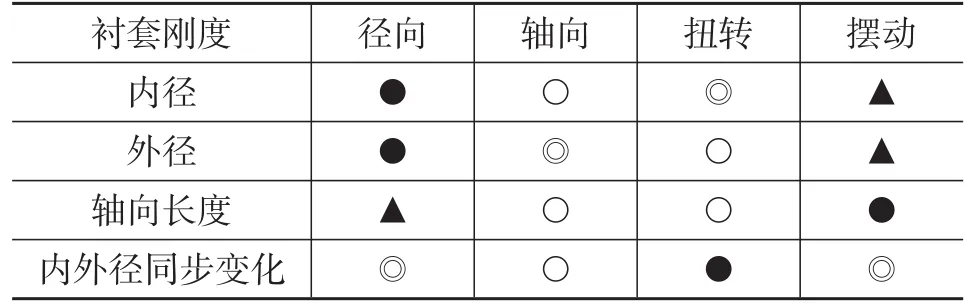
表6 各尺寸参数对衬套刚度的影响度

根据表6的结论可使衬套设计人员对工程知识积累及设计经验的依赖度大大降低，提高各向刚度均与目标刚度吻合的成功概率。

4 衬套结构的半经验优化设计

4.1 半经验优化设计流程

表2～表6为半经验设计提供了定性和定量的参考，使得衬套的半经验设计相对传统的设计方法具有更好的可操作性和成功率。衬套的半经验设计流程如图9所示。

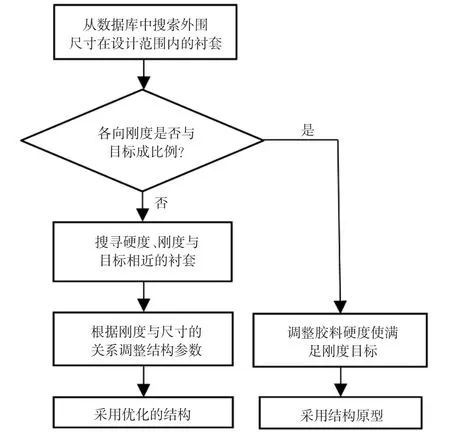
图9 半经验设计流程

具体实施方法为：首先从数据库中寻找外围尺寸在设计范围内的衬套，然后查看各向刚度与目标刚度是否成比例，如数据库中存在符合比例要求的衬套则采用该衬套，通过刚度比例关系调整胶料硬度，使其满足设计目标；如数据库中不存在符合比例要求的衬套，则转而寻找橡胶硬度及刚度相近的衬套，根据各尺寸参数对各向刚度的影响程度进行结构优化设计，使其各向刚度与目标刚度吻合，

4.2 衬套半经验优化设计方法的应用

以某B级轿车下摆臂衬套的设计为例，该摆臂衬套径向、轴向、扭转、摆动的刚度目标分别为5 000 N/mm、420 N/mm、1.5（N·mm）/（°）和12.0（N·mm）/（°）。外部尺寸要求为：橡胶内径不小于20 mm，橡胶外径不大于48 mm，橡胶轴向长度为26～58 mm。

根据设计目标要求采用半经验设计方法进行设计，首先从数据库中寻找外部尺寸在目标尺寸范围内的衬套，并对比各向刚度是否比例一致。通过对比，图2所示尺寸的衬套可作为设计原型衬套。

先对比目标刚度与初始刚度的差异，由目标刚度相对初始刚度的偏差（表7）可知，径向刚度和轴向刚度分别需要上调50.29%和29.23%，扭转刚度和摆动刚度分别需要上调14.5%和200%。

表7 初始刚度与目标刚度对比结果

根据前述分析，每一个尺寸的变化都会带来各向刚度的变化，但每个尺寸对各向刚度的影响量不一致，可通过调整影响最大的量去平衡各向刚度的变化。调整方法为：先增大轴向长度以提升摆动刚度，同时其它各向刚度也得到相应提升；然后通过调整内径或外径尺寸来调节径向刚度，同时补偿其它刚度。

将式（2）变化为以下形式：

将摆动刚度的需求变化率200%及摆动刚度的φk代入式（3），计算得轴向长度调整量β为50%，进一步计算轴向尺寸为37×（1+50%）=55.5 mm，再根据式（2）求得第1步调整后的各向刚度相对变化率φk0（表8），根据φk0可继续预测调整后的衬套各向刚度值。同时调整CAE模型，计算长度变化后的实际刚度值如表8所列。

将目标值与第1次调整后的刚度值对比，求出目标刚度与计算刚度的偏差，如表9所列。由表9可知，第1次调整后，径向刚度的需求调整量较大，轴向刚度的需求调整量最小。根据表6，内径变化对径向刚度影响最大，对轴向刚度影响最弱，符合此次的调整需求。

表8 第1次调整后各向刚度

表9 第1次调整后各向刚度偏差

由表9可知，内径应该向负方向调整，以保证各向刚度均减小。再参考表2中内径朝负方向调整的刚度变化率和式（3），可计算得内径需调整至约22.3 mm，此处取整将内径从24 mm调整为22 mm，取整后的内径变化率为0.83%。然后根据式（2）计算预测φk0，进一步计算得预测刚度值，结果如表10所示，由表10可知，预测刚度值与实际计算刚度值几乎一致。

同理，将第2次调整后的各向刚度与目标对比，结果如表11所示，由表11可知，各向刚度的偏差都在10%以内，已经满足工程设计15%的要求。

表11 第2次调整后各向刚度偏差

为达到更好的效果，进行了第3次调整。根据表11，径向刚度的偏差最大，轴向、扭转及摆动的偏差较小，且扭转刚度偏差与其它方向相反，因此，其它方向刚度调大时，需要对扭转刚度的影响尽可能小。依据表6，通过调整外径既可以使径向刚度调整量最大，也可使得扭转刚度变化最少。根据外径调整的刚度相对变化率φk，当将外径从40 mm减小为39.6 mm时各向刚度可满足要求，偏差在5%以内，预测刚度值见表12。

对比第3次调整后刚度与目标刚度值，径向、轴向、扭转、摆动的偏差分别为-3.8%、0.5%、2.0%和1.7%均在5%以内，远低于工程设计的±15%要求，至此完成该衬套的半经验设计，最终的内径、外径及轴向长度尺寸分别为22 mm、39.6 mm和55.5 mm。需要说明的是，橡胶衬套在工程设计时允许刚度存在15%偏差，因此这并不是唯一解，不同的调整思路可能会得到不同的结果，但各尺寸会大体一致。

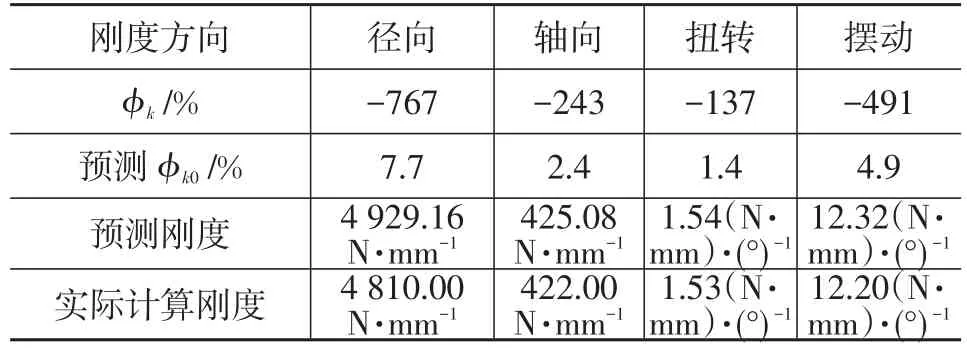
表12 第3次调整后各向刚度

5 结束语

针对尺寸参数与橡胶衬套各向刚度的关系进行了分析，基于此提出了橡胶衬套半经验优化设计方法，并采用该方法对某衬套进行了结构设计和优化，通过尺寸调整使其各向刚度与目标刚度的偏差都在5%以内，远低于工程设计的±15%要求。橡胶衬套半经验优化设计方法至少可保证3个方向刚度与目标吻合，具有较高的精度，可有效应对橡胶衬套结构设计时刚度匹配的难题，操作简便，所需调整次数少，工程应用价值较高。