车联网环境下公交发车间隔优化方法研究

殷巍,左忠义,张蕴琦,牛帅

(大连交通大学 交通运输工程学院，辽宁 大连 116028)

0 引言

随着经济的发展，小汽车的数量逐年增加.机动车在出行的过程中，除了给人们带来便利的同时，也带来一系列的交通拥堵问题.面对这种环境，公共交通逐渐被人们重视起来.在公交运营过程中，提高公交运营效率的关键就是实时解决公交的调度问题.随着智能交通的快速发展，交通智能化在公交系统中逐渐被重视起来.以车联网为基础的公交之间的相互通信，可以使驾驶员与乘客之间共享实时的交通信息，通过对公交实时定位，可以对车辆的速度、位置进行采集.虽然智能交通在公交领域已经逐渐引起了重视，但在实际中，对公交调度时刻表的编制仍然采用经验与实验相结合的办法.这种方法具有很大的盲目性，不能保证公交的运营效率.车联网的出现可以很好地对道路上的交通信息以及车内状况进行采集，对公交发车时刻表的编制具有积极的意义.目前关于公交发车时刻表的优化国内外有很多研究，但基于车联网的公交时刻表的编制还很少.2012年，Petersen在真实乘客到达数据的基础上，采用大邻域搜索对公交发车调度时刻表优化问题进行求解[1].2013年，Wagale按乘客需求和运行时间对公交问题进行建模，其乘客候车时间为公交发车间隔的一半[2].2014年，Saharidis针对公交发车调度时刻表问题建立了以乘客候车时间为目标函数的混合整数线性模型，其求解方法为启发式算法[3].2015年，Herbon在乘客满意度和公交运营成本的基础上，对公交发车时刻表的问题进行了具体的研究[4].在国内，2013年，穆礼彬结合公交卡数据对公交运行时间进行了确定[5].2011年，姚宝珍建立了以乘客利润和公交利润为目标函数的公交发车调度时刻表模型并采用启发式算法进行求解，该模型可以有效平衡乘客与公交公司之间的利益，可以提高公司运营效率[6].2008年，于滨等人采用支持向量机和卡尔曼滤波法算法对公交车辆到站时间模型进行了研究，该模型考虑了时间段、天气以及路段状况[7].2009年，马万经、杨晓光等针对公交优先采用动态规划方法对公交运行过程进行了研究[8].2015年，魏明等针对公交车及地铁、长途客运之间的换乘衔接建立发车间隔模型[9].叶清[10]等分别建立了基于乘客满意度和车辆台数约束的公交发车间隔优化模型.代存杰[11]等主要从时间需求下进行多车型快速公交发车频率的研究.王雪然[12]等主要基于服务水平，对纯电动车快速公交的发车间隔进行研究.赵淑芝[13]等主要从多种车型进行考虑，进行常规公交线路发车频率优化模型的研究.

上述研究从多种角度和条件在公交发车间隔设计方面取得了进展，但是在车联网的基础上研究时刻表的优化较少，以及忽略了车内拥堵系数对公交运营优化的影响.在实际运行过程中，往往会因为在某一站上的乘客过多，导致车内拥堵系数过高，进而降低公交的吸引力及服务水平.因此,本文在车联网的基础上，提出一种考虑车内拥挤成本的时刻表优化模型，并通过仿真实验分析来评估该模型对时刻表优化的效果.

1 公交发车时刻表模型的建立

1.1 模型的假设

由于公交调度受多种环境因素的影响，因此在进行模型的建立时，需要对外部的环境进行理想化概括.因此，做出如下假设：

(1)线路上的公交车型一致，站点上的候车环境基本相同；

(2)道路环境畅通，无交通事故的发生，公交车按时刻表依次发车，依次到达；

(3)车联网环境下，信息的传递与接收不存在延迟现象；

(4)车联网环境下，可以实时的对公交车在每一站的上下车人数以及到站时间进行预测；

(5)公交车的发车间隔是相同的；

(6)只针对单一的公交线路，不存在公交换乘现象；

(7)公交车的满载率一定，超过满载率，只能等待下一辆公交车.

1.2 模型建立

在建立公交发车时刻表模型时，主要考虑乘客和公交运营者的双重利益.其中，以等车时间成本最小、乘客的舒适度最大为目标函数，以公交的满载率为公交公司的目标函数，建立如下模型：

(1)乘客候车时间成本

乘客在k时段i站的等车时间为WTik

(1)

对整条公交线路，乘客总的等车时间函数为

(2)

乘客总的等车成本为

(3)

其中，i为公交车站的编号，k为时间段，Δtk为k时间段内的发车间隔，Pik为公交站点i第k时间段内的上车乘客数量；γ1为乘客等待时间损失费用，λik表示公交站点i第k时间段内的乘客到达率.

(2)乘客拥挤成本

乘客在乘车过程中，拥挤成本可以通过乘客的不舒适性或不方便性表示出来.乘客拥挤只有在某一站点上车的乘客数与公交车总体载客量的比例超过车内拥挤系数(ICF)才能体现出来，即：

(4)

乘客的拥挤路程函数为:

(5)

因此，乘客的拥挤度成本为：

(6)

其中，Q座位为公交车座位数，Q容为公交车额定量，Fk为k时间段内的发车频率；Qikp为表示公交站点i第k个时间段内第q辆乘客处于拥挤状态的车辆断面的客流量，c为公交拥挤站点，l为相邻公交车站的距离，γ2为乘客拥挤成本费用.

公交公司的运营成本主要是指公交在公交站点进行停靠时，公交通过加减速过程额外增加的磨损和电耗以及对车辆进行维修、车辆折旧和工作人员的工资等一些可变成本.这里不考虑公交运营的固定成本，因为固定成本对模型的构建没有影响.公交的运营成本如式(7)表示

(7)

其中，Tk为第k时间段内的总时间长度，L为线路总长度，e为乘客平均下车时间，常量；b为乘客平均上车时间，常量；δ为车辆加减速时间，常量；B为在车站上车的乘客数量，E为在车站下车的乘客数量，λ为公交公司成本折算时间价值系数，γ3为公交每单位公里的平均消耗的费用.

1.3 约束条件分析

在公交发车时刻表模型中，主要的约束条件为公交发车间隔约束、公交车站发车总次数的约束以及公交车的平均满载率的约束.

发车间隔约束：公交在早晚高峰以及平峰阶段，发车间隔是不同的，在早晚高峰期间，根据流量的不同，发车间隔应该小于5 min，在平峰期间，发车间隔小于15 min[14].

Δtkmin≤Δtk≤Δtkmax

(8)

发车总次数的约束：公交公司发车的总次数不大于最大的发车总数，即

(9)

平均满载率约束：为了保证公交公司的运营成本，公交车的平均满载率应大于公交线路所规定的最低满载率.当满载率为50%时，公交车的座位正好全部坐满[15].因此，取50%为公交满载率的下限，即

ICF≥0.5

(10)

所以时刻表优化的总体模型为

籍此次活动，天王表也再次践行公益之心，与百大名品中心温暖携手，一同向蚌埠特殊教育中心进行爱心捐赠，再次彰显了品牌的责任担当。

minX=ω1X1+ω2X2+ω3X3

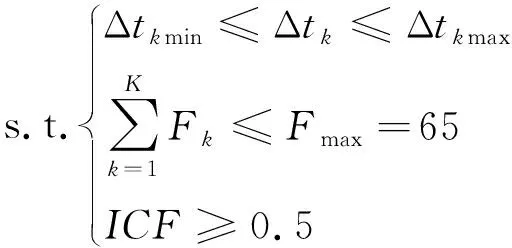
(11)

式中,ω为各指标利益的权重.

2 案例分析

本文基于大连市101线路为研究对象，对模型的正确性进行检验.101线路为大连市无轨电车，起始终点为马栏广场——大连火车站，全程7.5km.运营时间为4∶05～23∶25，对101线路的上下车人数进行人工调查，调查时间为晚高峰，发车间隔为4～5 min.上下车人数数据如表1所示.

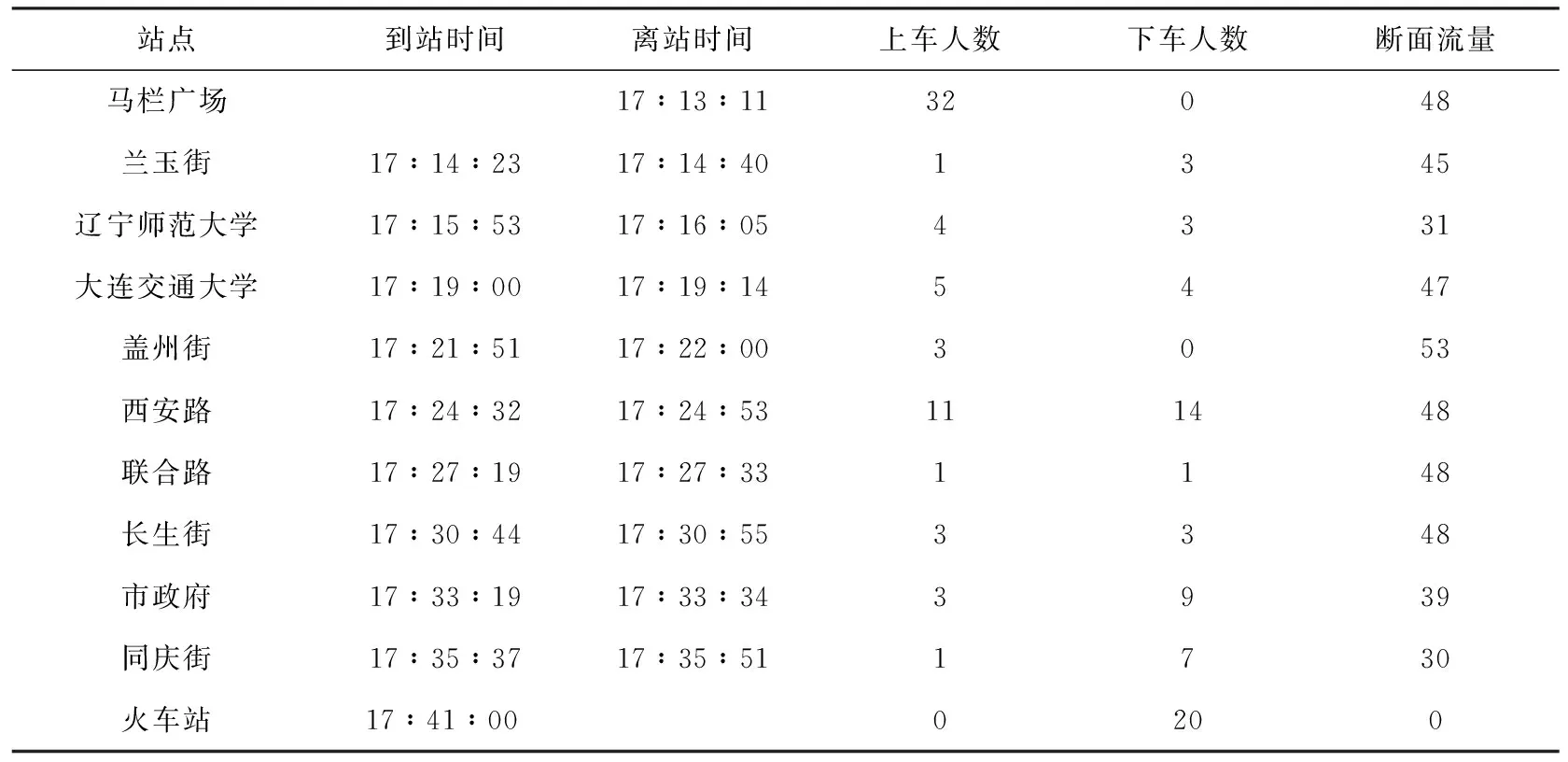
表1 马栏广场——大连火车站调查数据

大连市101公交线路具体走向及相邻站间距如图1及表2所示.

图1 101线路走向

表2 101线路相邻站间距

2.1 基本参数设置

(1)电车最大发车间隔Δtkmax=20 min，Δtkmin=2 min.101公交的载客容量Q载客量=90，座位数Q座=32.乘客可接受的拥挤程度的上限ICF=50%；模型的其他参数：乘客等待时间损失费用系数γ1=2.33；乘客拥挤成本费用系数γ2=0.024 173 57[16]，公交每单位公里消耗的费用γ3=3.33，λ=857 s/元，δ=30 s，e=b=2 s.

(2)遗传算法参数的设计

对遗传算法相关参数进行确定，种群规模M=100；循环次数T=250；交叉概率Pc=0.45；变异概率Pm=0.002.

2.2 优化结果

根据目标函数中权重取值的不同，所得出的优化结果是不同的.如表3所示.

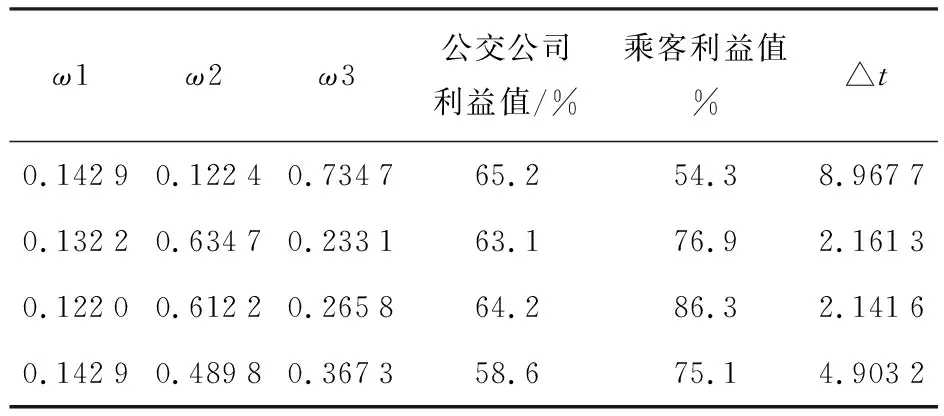
表3 不同权重的取值

对应的仿真图形如图2所示.

由2(a)可以分析出，当权重偏向于公交公司时，发车间隔越大；由图像2(b)可以分析出，当权重偏向于乘客时，发车间隔就越小.由图2(c)、2(d)进行对比分析可以看出，当目标函数中的权重偏重于乘客时，乘客的等车时间成本及拥挤度成本较小.当目标函数中的权重偏重于公交公司时，乘客的等待时间成本及拥挤成本就越高.本文构建的模型与传统的模型相比，更能体现出公交拥挤成本对发车时刻表的影响.构建的模型具有良好的收敛性，可靠性较强.

(a)

(c)

(d)

3 结论

根据目标函数中权重取值的不同可以看出，当权重偏重于乘客时，发车间隔就越小；当权重偏向于公交公司时，公交的发车间隔就越大.通过优化发车间隔，101电车的发车间隔高峰期间应取3min.通过合理的发车间隔的优化，不仅可以提高公交的社会效益，还可以增加公交的经济效益.本文在充分考虑发车间隔、发车次数、车辆满载率约束条件下，对城市公交发车调度时刻表进行研究.在综合考虑约束条件的基础上，以乘客候车时间、乘客舒适度以及公交公司运营成本最小为目标函数，建立公交发车调度时刻表优化模型.本文的不足之处在于，所调查的数据仅为101的晚高峰数据，目标函数还有待进一步的完善，在今后的研究中，应该对影响乘客及公交公司的多方面因素更加全面地进行分析.