基于可靠性的地铁车齿轮箱维修周期优化

李雨晗,李永华,宫琦

(大连交通大学 交通运输工程学院，辽宁 大连 116028)

0 引言

地铁车齿轮箱预防性维修的关键在于合理确定其维修周期，过短的维修周期会产生过剩维修，造成人力和资源的浪费；而维修周期过长则会导致欠维修，不能有效防止故障的发生，影响车辆运行的可靠性[1].传统的预防性维修采用等周期的检修方法，认为系统的故障率不受维修工作的影响[2].实际上维修不能使系统修复如新，随着役龄增加，系统的故障率不断升高，可靠性逐步降低，导致维修间隔越来越短，运行成本及附加成本增加，甚至影响到车辆的正常运行[3- 4].目前有一些学者对维修周期进行了研究，韩帮军等[5]构建了基于等效役龄的概念、在有限时间区间内和可靠度约束下的维修周期优化模型并求解，结果表明系统的预防性维修周期不再是等周期，而是随着故障率的提高不断缩短；夏唐斌等[6]结合混合式故障率演化模型，按照有效度最大的原则确定了港口起重机械的最佳维修周期，但是缺少对维修经济性的考虑；王灵芝等[7]综合考虑了两种调整因子的优点，建立使系统有效度最大化的预防修经济优化模型，求解得到系统的最佳维修周期，但忽略了对车辆运行和维修的总时间进行约束.本文综合考虑了车辆可靠、经济的运行要求，基于混合式故障率演化模型描述地铁车齿轮箱各部件的故障率，建立以维修成本最小为目标，以可靠度和维修时间为约束的维修周期优化模型，运用Matlab2015b编程，采用基本遗传算法求解，确定符合可靠度要求、且维修成本得到优化的地铁车齿轮箱维修周期.该优化模型得出的结果更加贴近实际，为齿轮箱最佳维修周期的确定提供了参考.

1 地铁车齿轮箱的故障分析

作为转向架系统中发生故障频次较高的部件，齿轮箱对车辆的正常运行产生了重要的影响.基于对车辆维修数据的统计，根据故障模式分析齿轮箱主要部件发生故障的原因[8-9]，以评估故障对车辆运行的影响，分析结果见表1.

可靠性框图从可靠性的角度出发，研究了系统和部件之间的故障逻辑关系，表达的是系统各部件发生故障时对系统状态的影响.齿轮箱为串联结构，其可靠性框图如图1所示.

表1 齿轮箱主要部件故障模式及故障原因

图1 齿轮箱可靠性框图

由图1可知，齿轮箱主要由传动轴、轴承、齿轮箱箱体和齿轮副组成，每个部件出现故障都会造成齿轮箱的故障[10].采用二参数的威布尔分布描述齿轮箱的故障规律.假设传动轴、轴承、齿轮箱箱体、齿轮副的失效率分别服从不同参数的威布尔分布[11]，并假定它们的分布参数分别为m1,η1、m2,η2、m3,η3、m4,η4，则齿轮箱各部件的故障率为：

(1)

式中，mi和ηi分别代表形状参数和尺度参数.

假定各部件故障相互独立，将齿轮箱的总故障率看作四个部件故障率叠加值，即：

(2)

式中，λ1(t),λ2(t),λ3(t),λ4(t) 分别代表传动轴、轴承、齿轮箱箱体、齿轮副的故障率，λ∑(t) 表示齿轮箱的故障率，服从指数分布.

建立维修模型的关键在于求解维修周期内系统的故障率函数.役龄递减模型描述的是开展预防性维修后系统的初始故障率，反映修复非新的情况，而故障率递增模型描述了系统的功能衰退速率.基于此，混合式故障率演化模型可以较好地描述预防性维修前后系统故障率的变化情况[12].

当齿轮箱采取预防性修理时，按照役龄递减因子理论[13]，经过第j次预防性维修后的故障率为：

λj+1(t)=λj(t)·(t+aTj)

(3)

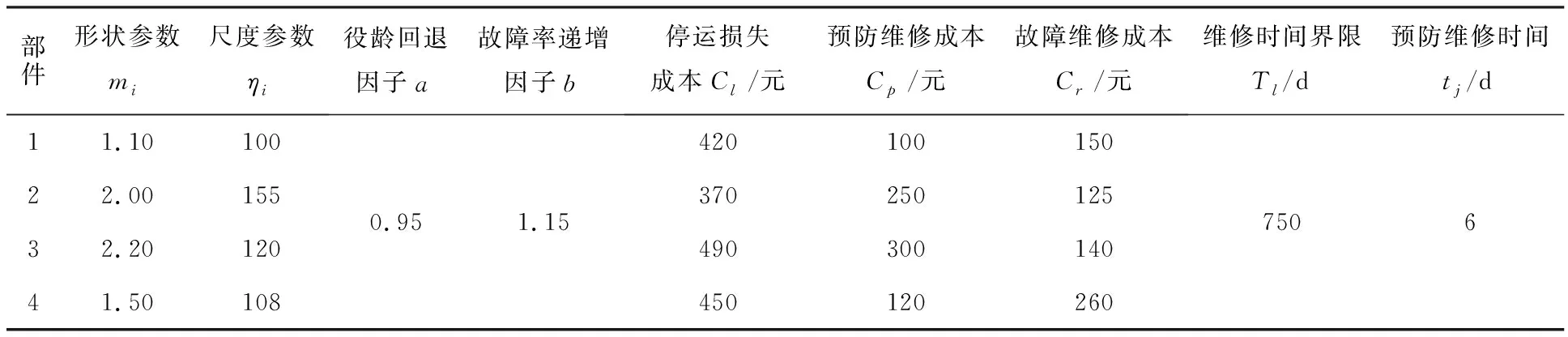
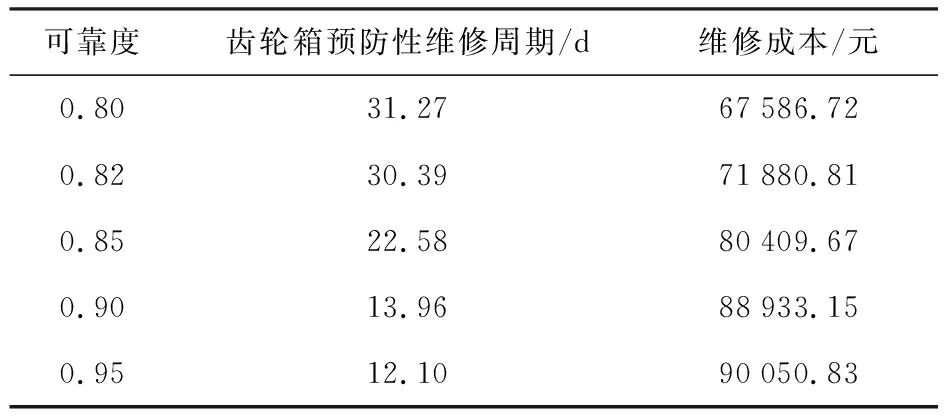
式中，0

进行预防性更换时，基于改善因子理论，维修后故障率为：

λj+1(t)=b·λj(t)

(4)

式中，b>1为故障率递增因子，t∈(0,Tj+1) .该理论表明预防性更换后其初始故障率会减小为零.

假设齿轮箱在预防性维修周期内出现故障，基于混合式故障率演化模型的理论，假定相邻两个预防性维修的周期满足Tj+1≈aTj， 则在一个完整的预防性维修周期内，齿轮箱故障率函数表示为：

(5)

第j个预防性维修周期内发生的总故障为：

(j=1,2,3,…,n)

(6)

2 齿轮箱维修成本分析

合理规划维修间隔可以有效减少故障的发生次数以及降低事后维修的成本，地铁车齿轮箱总维修成本主要由故障维修成本、车辆停滞运营损失成本和预防性维修成本组成[14].

(1)故障维修成本

齿轮箱故障维修成本表示为单次故障维修成本与一个维修周期内总维修次数的乘积，即：

(7)

式中，Cr表示齿轮箱发生单次故障维修成本.

(2)停滞运营损失的成本

停滞运营损失的成本是指每次维修时，铁路停运导致的损失，表示为：

(8)

式中，Cl表示单位时间内损失的成本，tj为第j次预防性维修的时间.

(3)预防性维修成本

预防性维修成本是对齿轮箱进行预防性维修时花费的成本，表示为回退量a、递增量b和维修间隔T的函数，表示为：

(9)

式中，Cp(a,b,T)是关于a,b,T的函数，表示第j次预防性维修的成本.

在建立齿轮箱的预防性维修周期优化模型时，还应该满足的约束条件为[15]：

(1)每次开展预防性维修后，齿轮箱的可靠度应大于给定的可靠度下限；

(2)列车的运行时间及维修时间之和在限定的时间内.

可靠性是指系统稳定工作不发生故障的概率，地铁车齿轮箱的预防性维修要保证在各维修周期内都具有一定的可靠度，其在各预防性维修周期内的可靠度为：

(10)

以维修成本最小为目标，可靠度和维修时间为约束条件，建立齿轮箱的维修周期优化模型为：

min(CR+CL+CP)

s.t.Rj≥limR

(11)

式中，limR表示可靠度下限；Tl表示限制的维修时间界限.

3 算例分析

以某地铁车齿轮箱为例，该齿轮箱主要由四个部件组成，构成一个串联结构，各部件的故障率服从式(2)的威布尔分布，且齿轮箱各部件均以全新的状态运行.基于文献[16-18]的故障数据，给定齿轮箱的最低可靠度为0.80，各部件的具体维修参数见表2.

表2 齿轮箱各部件维修参数

根据表2中的参数对整个齿轮箱进行以可靠性为中心的预防性维修，即各部件的维修周期是相同的.一旦到达维修周期，就要对各部件同时开展预防性维修.根据式(11)，运用Matlab2015b编程，采用基本遗传算法求解模型，计算得到维修周期和成本见表3.

表3 齿轮箱维修周期及维修成本

由表3可知，维修成本随可靠度要求的提高而增加，维修周期逐渐缩短.运用基本遗传算法求解优化模型，得到不同可靠度约束下齿轮箱各部件的预防性维修周期以及维修成本，结果见表4.

表4 不同可靠度约束的齿轮箱各部件维修周期及维修成本

由表4可以看出，齿轮箱各部件的维修周期是有区别的，即地铁车齿轮箱进行维修时，是针对某一部件而不是对整体进行的维修.由于各部件的性能不同，当地铁车齿轮箱进行预防性维修时，只要维修性能最低的部件，避免了维修整个齿轮箱而造成不必要的维修费用，且更加符合工程实际.与维修整体相比，该方法能够有效地节约维修成本，成本节约率最大可达19.04%.

提高齿轮箱的性能要以维修成本为代价，在实际运行时需要综合考虑可靠度和维修成本以确定最合适的维修周期.可靠度与维修成本的关系如图2所示.

图2 可靠度与维修成本的关系

由图2可知，维修成本随着可靠度的提高而不断增加，当可靠度为某一定值时，齿轮箱整体的维修成本高于针对各部件的成本.因此，按照齿轮箱各部件服从不同参数分布规律建立的维修周期优化模型不仅更加贴近工程实际，而且能够有效降低维修成本.实际制定维修计划时，需要综合考虑可靠度和维修成本等因素，确定最合适的地铁车齿轮箱的维修周期.

4 结论

本文采用不同参数的威布尔分布描述地铁车齿轮箱各部件的故障率，建立了基于可靠度约束的预防性维修周期优化模型，运用基本遗传算法编程求解模型，得到的结论如下：

(1)克服了以往假定整个结构服从同一参数分布的方法的弊端，文中将齿轮箱各部件的故障率等效为不同参数的威布尔分布，地铁车齿轮箱进行预防性维修时，每次只需要维修性能最低的部件，有效地延长了维修周期且节约了维修成本；

(2)过高的可靠度要求会增加齿轮箱的维修成本，维修周期也随着可靠度的增加而不断缩短，则维修愈加频繁.在工程实际中要根据车辆运行的要求，综合考虑可靠性、维修时间和维修成本等因素，合理确定齿轮箱各部件的维修周期；

(3)该优化模型可以有效降低齿轮箱的维修成本，更加贴近实际，对以经济性和可靠性为要求的地铁车齿轮箱维修周期的确定提供了一定的指导意义.