对教师资格考试的分析与思考——以数学学科知识与教学能力（高级中学）为例

胡典顺 邵贵明,2 朱梦琪 朱晓语

（1.华中师范大学，武汉 430079；2.黄冈师范学院，湖北黄冈 438000）

20世纪80年代以来，教师专业化发展成为世界各国广泛关注的热点之一，教师资格考试制度的建立是教师专业化发展的必然要求。2011年教育部公布《关于开展中小学和幼儿园教师资格考试改革试点的指导意见》，在湖北和浙江两省启动全国教师资格统一考试试点工作，并提出“试点工作启动后，2012年及以后的师范类专业学生，申请上述教师资格者，须参加教师资格考试”[1]。目前该考试分为幼儿园、小学、初级中学、高级中学和中职5个类别，考试形式分笔试和面试2部分。其中，初级中学、高级中学笔试科目均为综合素质、教育知识与能力、学科知识与教学能力3科。

目前针对教师资格考试已有一些研究成果，对制度和教师发展方面的研究较多，对教师资格考试试题本身的研究较少，本文拟通过对2012年下半年至2017年上半年共10套数学学科知识与教学能力（高级中学）考试笔试试题进行统计分析，以期为教师资格考试科学发展、师范教育教学改革提供参考。

1 数学学科试题框架内容及分析

通过分析教师资格考试“数学学科知识与教学能力（高级中学）”的内容框架，能够了解我国教师资格考试对教师专业化的基本期望，可以揭示数学教育理论与实践层面对普通高中教师的基本要求。

本文根据考查内容将考试试题分为数学学科知识、数学教育理论、数学教育实践3大模块来进行统计分析。试卷有6种题型：选择题（第1～8题，共8题）、简答题（第9～13题，共5题）、解答题（第14题，1题）、论述题（第15题，1题）、案例分析（第16题，1题）以及教学设计（第17题，1题），全卷共有17道题，总分150分。3大模块分布状况为：数学学科知识（共10小题，61分）分布在选择题第1～6题、简答题第9～11题和解答题第14题，数学教育理论（共5小题，39分）分布在选择题第7～8题、简答题第12～13题和论述题第15题，数学教育实践（共2小题，50分）分布在案例分析和教学设计。

1.1 数学学科知识分析

根据试题的考查内容，把数学学科知识分为数学分析、高等代数、空间解析几何、概率与统计以及中学数学5个部分。由于这几部分知识之间较容易辨别，文中就不举例加以说明。它们的题型和题量统计见表1。

由表1可知，从题目数量来看，数学分析和高等代数在数学学科知识中所占比重较大，二者相加超过数学学科知识的一半，空间解析几何、概率与统计、中学数学三者题量之间差别不很明显，数学分析在数学学科知识选择题中题量最多，其次是高等代数，概率与统计较少，10套试题中解答题共有10道，数学分析、高等代数各出现4次，占明显优势。

从数学学科知识各部分分数所占的百分比来看，数学分析和高等代数较高，二者均超过了25%，相加超过了55%。数学分析、高等代数、空间解析几何3部分占总分的72.79%，而这3部分在大学一、二年级已经修完，这说明国家规定在大学二年级可以参加教师资格考试是合理的，同时说明提高师范生高等数学水平，是将来从事基础教育的必要条件。

从命题趋势来看（见图1），有8次考试中数学分析和高等代数分值超过数学学科知识部分的一半以上；从2012年下半年到2014年上半年和2015年上半年出现了中学数学知识，且在2013年上半年试题中中学数学知识超过一半以上，这在全部10套试题中较为罕见；从2015年下半年开始以后的试题中，数学分析、高等代数、空间解析几何以及概率与统计的分值逐步趋于平稳，中学数学知识没有出现，试题结构逐步趋于稳定。

表1 10套试题中数学学科知识分类及题量、分值统计

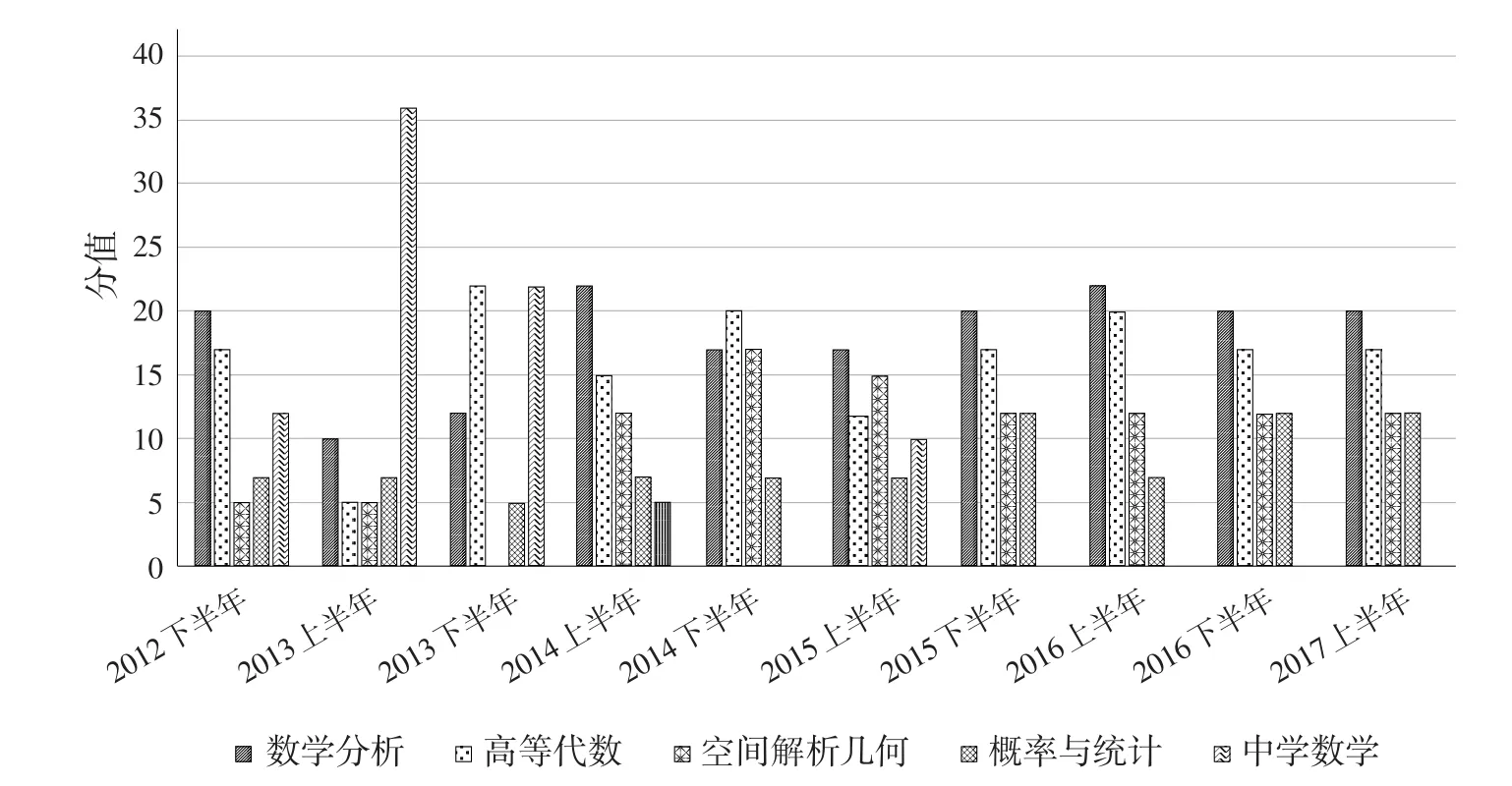
图1 10套试题数学学科知识分值变化趋势

1.2 数学教育理论分析

根据考查内容，我们把试题中数学教育理论分为课程知识与教学知识2个部分。课程知识包括课程标准、课程内容、课程理解以及课程文化；教学知识包括教学组织、教学原则、教学评价以及教学内容。将10套试题中数学教育理论模块涵盖的题型和题量作了统计（见表2），一方面可以检验命题是否具有稳定性，另一方面可以对课程知识和教学知识的考查方式和考查重点进行分析。

由表2可知，数学教育理论模块中，课程知识的题目明显多于教学知识的题目，约为2倍关系，特别是关于高中数学课程标准的试题在所有分类小项中是最多的。同时，教学知识部分中，教学原则、教学评价以及具体的高中数学教学内容的题量大致相当。

总体来说，10套试题中教育理论方面分值位列前5位的依次为课程标准、课程内容、课程理解、课程文化以及教学评价。根据逐年变化趋势来看，关于高中数学课程标准试题前些年所占比重较大，而2016年下半年和2017年上半年考试试题中没有出现。综观各年试题分布情况，有6次考试比较集中在3～4种知识类型，覆盖知识类型最多的也只有2次考试覆盖了5种类型，并不是每次考试都能覆盖所有类型教育理论的知识。一方面从客观上来说教育理论涵盖面广，涉及的学科知识很宽泛；另一方面仅仅通过几道题目来测试考生在这方面的水平，命题难度较大。历年考试试题在该部分变化较大，呈多样化趋势，但也说明考试试题的稳定性有待加强。

1.3 数学教育实践分析

数学教育实践只有案例分析和教学设计2个题目，将试题中数学教育实践分为案例分析与教学设计2个部分。

对于案例分析试题，试题呈现方式均是对教学片段的分析。根据案例涉及的教学内容，将它分为概念教学、命题教学、解题教学3个方面，10套试题中各方面出现的频率为概念教学2次，命题教学（含公理定理、公式法则等）3次，解题教学5次。10套试题中解题教学出现频率最高，说明考试重点突出考查考生对解题的熟练程度、数学认知能力、数学思维过程和对正确解法或错误解法的辨析以及要求考生提供另外的解法等。在教学内容总类别下，从试题考查方式涉及教育理论知识的侧重点来看，可以将它分为教学技能、数学思维、数学思想方法3个方面，有的试题涉及其中2个侧重点；10套试题中各方面出现的频率为教学技能6次，数学思维4次，数学思想方法2次。关于教学技能，考查了导入技能、提问技能以及组织调控技能，没有突出考查语言技能、讲解技能等。

表2 10套试题中数学教育理论分类及题量统计

对于教学设计，试题呈现的主要方式为：针对教学内容的某一课题，进行教学设计分析。首先我们同样按照对应的教学内容的类型分为概念课、命题课和数学解题课3个方面，10套试题中出现的频率分别为概念课6次，命题课3次，数学解题课1次，以概念课考查为主。在教学内容总类别下，从试题考查方式涉及教育理论知识的侧重点来看，考查了教学目标、重难点、学情分析、内容分析、数学应用、教学过程设计、设计意图7个方面。统计发现，该部分有8次考查了对具体教学过程某一环节的设计。此外，教学目标、重难点以及内容分析占主要地位，特别是2014年上半年仅仅考查了教学目标这一个方面，包括对教学目标的理论理解、表述方式、教学定位、具体教学课题下教学目标的制定。根据统计可以发现前期的3次考试突出强调了设计意图的考查。

除了对教学设计部分进行分析以外，我们还对这些方面在试题中的分值进行了统计，其中将设计意图的分值包含到教学过程的环节中不单独列出。除了2014年和2015年下半年外，其余8套试题中，教学过程设计所占分值最大。这说明对于教师来说，制定教学目标，准确把握教学重难点，科学理解教学内容，进行科学化、多样化、情境化的教学设计，是将来站上讲台、站稳讲台、站好讲台的必要前提。

2 启示及思考

分析试题体现的内容框架和考查重点，可以明晰考试对教育的价值导向，认清基础教育对师资质量的基本需求。通过试题分析，可以发现教师资格考试本身尚需进一步改进，师范教学也需要进一步完善。

2.1 教师资格考试数学科应加强科学发展

教师资格考试从试点到正式考试已举行了10多次，虽然形成了比较规范的格局，但仍应寻求进一步的科学发展。第一，教师资格考试数学科突出考查了数学分析、高等代数、空间解析几何等高等数学基础知识，立足于要求考生以高起点面对中学数学，反映了国家对教师专业化的学科知识方面的要求；但是，这部分考试内容除了2013年上半年以外，其他少有甚至没有涉及高中数学知识，不利于师范生系统掌握高中数学知识体系，导致拿到了资格证书的师范生仍然不知高中数学内容前后逻辑关系，不利于将来快速适应教学，故应该逐步增加对高中数学核心内容知识的考查。第二，在数学教育理论方面，近些年的考题略显庞杂，这个模块的试题缺乏相对稳定性。一方面与教育理论本身涉及面广，考查难以兼顾各个层面导致命题难度大有关；另一方面也反映了在考核导向和命题思路上，考试对职前教师掌握教育理论期望过高。实际上，教育理论不同于单纯的数学知识的学习，学习教育理论不仅要经历厚积薄发的过程，而且需要在实践中逐步领悟提升。因此，教育理论考查应稳定在对部分核心的数学教育理论的考查，不必面面俱到。第三，在教育实践部分，案例分析和教学设计应以具体的重点中学教学内容为主，不必过分纠缠教育理论；考查内容同样也不必面面俱到，应重点围绕中学核心概念、数学思维、数学思想方法等展开，考查师范生是否善于引导高中生提升数学技能和思维品质，特别是通过教学实践试题来考查师范生是否善于提升高中生数学抽象、逻辑推理、数学建模等数学核心素养。

2.2 师范教育应关注国家政策导向

教师资格考试是一项教师职业准入式考试，通过考试试题可以洞悉国家政策导向：试题反映了国家的人才观，体现了现实教育的课程观，表明了基础教育的育人观；试题突出体现了国家对教师专业化的基本内涵要求，在学科专业性和教育专业性两方面，明确了精通学科知识是胜任工作的基本要求，宽厚的文化素养是出色完成教学工作的必要条件，教育学、心理学知识是教师出色完成教学任务的保证，实践知识则彰显教师作为专业人员的独特性[2]。此外，《普通高中数学课程标准（2017年版）》是对高中数学教学的指导性文件，因此所有教师要注重对课程标准的理解。教师资格考试中，无论是数学教育理论知识还是数学教育实践知识，都与数学课程标准内容密切相关，在师范教学中应注重对课程标准的解读和研究，提升师范生宏观掌握教育理论的能力。

2.3 师范教学应突出学科专业特色

通过试题分析可以发现：一方面师范教学要突出学科专业特色，增加“数学学科教学设计”等2～3学分的教育理论选修课程、数学信息技术课程，同时增加1～2学分的教学技能训练课程，反对简单减少师范生基础课程的课时来增加实践时间的方案，建议在数学分析等基础课程的授课形式上，对志愿从事学术研究和从事师范教育的学生分开要求，对于志愿从事学术研究的学生采用增加更多专题讨论的形式进行学科知识研究性学习，对于志愿从事师范教育的学生通过先学后教、师生共建、翻转课堂等多种模式共存的方式进行。另一方面要将数学学科理论与实践深度融合，改变通过教育实习和教学技能竞赛来提升实践能力的单一模式。师范教学技能竞赛也只能为少数学生提供平台，不利于整体素质的提高。此外，应该分期实践、多元实践与传统实践相结合，可以将实践时间分期，提前在大学二年级开设1～2次的1～2周见习，让师范生尽早熟悉中学课程体系，了解中等数学和高等数学的逻辑关联；同时丰富教学竞赛形式，建议增加教案写作、教学过程片段设计、数学解题、数学讲题、说课、基础教育数学考试分析等竞赛。这样有利于加强师范生整体综合专业化特色。