基于损失交换比的武器装备回合战斗力指数评估
薛 辉, 刘铁林, 张 鹏
(1. 陆军工程大学石家庄校区装备指挥与管理系, 河北 石家庄 050003; 2. 空军石家庄飞行学院, 河北 石家庄 050071;3. 61267部队, 北京 101114)
现代战争呈现出科技含量高、杀伤威力大,多兵种、多类型武器装备和多种战斗因素等特点,采用传统的经验估算法已难以有效地评估对抗双方的战斗力。目前,主要采用指数法进行武器装备战斗力评估,如杜佩方法、邓尼根方法、泰勒方法、战斗价值等效方法、概率统计法和指数-兰彻斯特方法等[1-2]。虽然,战斗力指数评估选取的参考对象更加多样,建立的评估模型更为合理,但大多数的战斗力指数评估模型要求在最有利于发挥武器装备战斗力的条件(射击条件最有利,使用人员技术水平最高,攻击对象充足等)下开展评估,且仍然是静态战斗力或战斗实力评估。因此,在实际作战中,若仍然根据静态战斗力值对战斗进程、战斗胜负、战斗损失以及装备保障需求进行预计,必然会造成巨大误差。
李璟[3]将武器装备战斗力分为战斗静力、战斗实力和战斗活力3种形式。在兵棋推演中,武器装备回合战斗力指数是指武器装备在一定时间的战斗过程中所表现出来的对对方装备的毁伤能力或对抗能力,其取决于己方的战斗实力及对方的作战力量编成。因此,武器装备回合战斗力指数评估不仅与武器装备自身的战技性能有关,还涉及使用人员的训练水平、对抗双方的交战态势、战场环境,以及由兵棋推演粒度、规模和推演目的决定的回合时间等,甚至还与对方武器装备作战计划密切相关。合理准确地评估武器装备回合战斗力指数,可为军事指挥员掌握双方的作战实力、制定作战计划、裁决兵棋推演双方的胜负概率、预测装备战损率以及装备保障需求提供参考依据;而且,若利用兰彻斯特方程,还可计算出双方的交战时间及交战进程等。
战斗活力是指在交战过程中,交战双方将自身具有的机械能、化学能以及人的体能和智能等能量,转化为实施进攻和防御军事行动的能力[3]。笔者以战斗活力为重点研究内容,在目前静态战斗力或战斗实力评估模型的基础上,结合双方的交战态势、武器装备型号、弹药类型以及回合时间等,基于武器装备的对抗损失交换比建立武器装备回合战斗力指数动态评估模型,实现武器装备回合战斗力指数的动态评估。
1 武器装备战斗力指数评估思路
武器装备作战能力是制定作战方案的重要依据。目前,在火力规划模型中主要将威胁度与毁伤概率结合,如文献[4-8]作者在火力分配优化建模中,建立了攻击m个目标的总体作战效果模型:
(1)
式中:ωj为第j个目标的威胁度;xij为第i个火力单元攻击第j个目标的弹药数量;pij为第i个火力单元对第j个目标的毁伤概率。
若运用智能算法求解模型,则根据最大毁伤概率和威胁度来寻优,假设ωj对于k个火力单元都是一致的(事实上同一目标对不同火力单元的威胁度存在很大差异),因此,运用智能算法开始计算时,倾向于规划较多的弹药对威胁度较大的目标进行攻击,然后,再根据毁伤概率进行适当修正。尽管智能算法可将威胁度与毁伤概率结合起来进行综合评估,但其历时较长,且仍然未能有效地解决目标威胁度的准确量化问题。笔者通过在武器装备与目标对抗能力之间建立一一对应关系,来体现同一目标对不同武器装备的威胁度不同、同一武器装备对不同目标的对抗能力也不相同的思路,并将二者相结合转化为武器装备战斗力指数。
同一武器装备使用不同的弹药对同一目标的毁伤效果也不同,如:某型坦克若使用反坦克导弹或穿甲弹,其对装甲类装备的攻击战斗效能很高,但对空中目标或单兵目标的攻击战斗效能却很低;若使用杀爆弹,其对单兵目标的攻击战斗效能很高,但对装甲目标或空中目标的攻击战斗效能却很低;如果使用的弹药种类与目标不匹配,则坦克难以正常发挥其战斗力,如使用杀爆弹打击坦克或使用穿甲弹打击步兵,其战斗力就很低,甚至为0。
综上所述,建立武器装备战斗力指数评估模型不仅要考虑武器装备自身固有的作战性能,还应在其使用的弹药种类与攻击的目标种类之间建立一一对应关系。因此,笔者在静态战斗力指数或固有战斗力指数评估的基础上,首先,采取对比法合理选取对抗中的武器装备作为参考对象,根据“预己从严、料敌从宽”的基本原则(对方战斗力最优原则),结合双方交战态势、武器装备的动态变化情况,采用基于武器装备对抗损失交换比的指数法实现武器装备作战效能的动态评估。其次,根据“聚焦作战、面向保障”的评估原则选取参考对象,并结合作战实际,使战斗力指数评估既符合武器装备的战技性能,又符合作战指挥员的军事意图。具体包括以下3个方面:1) 明确作战指挥员的作战意图,优先选取作战计划中指定的打击目标作为评估参考对象; 2) 确定评估参考对象之前,应先判断攻击目标是否在可攻击范围内,且满足1个回合的打击需求; 3) 结合武器装备保障实际,优先选取弹药携行量大且供应充足的目标作为评估参考对象。最后,结合弹药发射速率、命中概率以及兵棋推演回合时间,确定某种武器装备使用某种弹药在1个回合时间内对对方某种武器装备的战斗力指数,将时间量纲引入武器装备战斗力指数评估中,对比不同武器装备战斗效能的高低,并结合兰彻斯特方程预测对抗双方的胜负概率、作战持续时间以及双方作战实力随时间的变化情况等。
2 武器装备战斗力指数评估模型
假设红方(己方)、蓝方(对方)各有M、N种武器装备,红方第m(m=1,2,…,M)种武器装备对抗蓝方第n(n=1,2,…,N)种武器装备的最大损失交换比为Km∶Kn,该交换比也称为作战效能平衡点,即当红方利用Km个第m种武器装备与蓝方的Kn个第n种武器装备进行作战时,交战结果为平手,其极限情况为1∶0或0∶1,为此,可设Km+Kn=1。也可认为这就是2种武器装备交战时的相对战斗力指数。
定义Km∶Kn为2种武器装备的相对战斗力指数,Pmn和Pnm为2种武器装备直接交战的标准战斗力指数。若Pmn∶Pnm=Km∶Kn,则Pmn能否得以发挥,与对方是否投入了该种交战武器装备有关(即与作战目标有关),因此,2种武器装备的直接交战标准战斗力是否存在,与对方在同一作战时空内是否投入了该种武器装备有关。由此可假设2种武器装备的标准战斗力指数是否存在,与其武器装备投入和作战运用有关。
假设任何一方都会最大程度地发挥每种武器装备的战斗力指数,称为最大战斗力发挥原则。由于作战双方无法准确地获取对方的作战力量分配结果,因此,在进行火力分配优化时,通常只能根据打击目标可能的战斗力指数进行决策。若红方第m种武器装备对蓝方第n种武器装备的相对战斗力指数为Km∶Kn,可假设若蓝方第n种武器装备的综合战斗力指数为Pn,则根据战斗力最大发挥原则,蓝方第n种武器装备对所有存在交换比不为0的红方武器装备的战斗力指数均为Pn,同时,认为红方第m种武器装备对蓝方第n种武器装备的战斗力指数为Pn(Km/Kn);反之,若以红方第m种武器装备为参照对象,则双方的战斗力指数分别为Pm和Pm(Kn/Km)。由于在解决任何军事问题时,战斗力指数均采用对比值形式,如果对抗中仅有2种武器装备,则无论选取哪种战斗力指数都是合理的,其对比值-损失交换比始终不变。然而,在实际作战中有很多种武器装备参与,因此,笔者根据战斗力最大发挥原则选取二者中的较大值作为参照对象,来计算2种武器装备的标准战斗力指数,即max{Pm,Pm(Kn/Km),Pn,Pn(Km/Kn)}=max{Pm,Pn}。
由此可见:武器装备的动态战斗力指数不仅取决于武器装备的标准战斗力指数,还与2种武器装备之间的相对战斗力指数或损失交换比有关;此外,根据双方军事指挥员的作战意图,武器装备打击目标时带有很强的目的性,动态战斗力指数也与作战双方武器装备的火力分配(运用)情况有关。
2.1 武器装备动态战斗力指数计算模型
设红方参与对抗的武器装备集合为WH={WHm,m=1,2,…,M}={WH1,WH2,…,WHM},其标准综合战斗力指数矩阵PH=(PHm)1×M=[PH1PH2…PHM],蓝方参与对抗的武器装备集合为WL={WLn,n=1,2,…,N}={WL1,WL2,…,WLN},其标准综合战斗力指数矩阵PL=(PLn)1×N=[PL1PL2…PLN]。在分析2种武器装备的对抗损失交换比时,还应考虑所用弹药的不同。设红方武器装备可用的弹药有D种,蓝方有F种,红方武器装备WHm使用第d(d=1,2,…,D)种弹药与蓝方武器装备WLn使用第f(f=1,2,…,F)种弹药的对抗损失交换比为kmd∶knf,由于作战双方可通过火力分配来规划己方使用的弹药种类,但无法预知对方使用的弹药种类,因此,根据对方战斗力最优的原则,假设蓝方武器装备会使用威胁程度最大的弹药,红方武器装备应取kmd∶knf最小的交换比(同理,蓝方武器装备相应地取knf∶kmd最小的交换比)作为计算双方相对战斗力的依据,但若任何一方的武器装备无法使用该种弹药时,将无法进行对抗,则定义交换比为-1,即kmd∶kn=min{kmd∶knf|f},其比值与另一方武器装备所用的弹药无关。因此,红方武器装备WHm在使用第d种弹药对抗蓝方武器装备WLn时,基于对抗损失交换比的战斗力指数Pmnd的可能取值有PLn(kmd/kn)、PLn、PHm,其最终取值的计算步骤为:首先,在PLn(kmd/kn)、PLn二者中取较小值;然后,与PHm对比,在二者中取较大值。取较大值是为了避免与对方武器装备直接对抗时,二者分别计算的战斗力指数相对值发生不对等的情况。这样,就可分别获得武器装备采用不同弹药与对方武器装备对抗时的对抗战斗力指数。
为了便于使用MATLAB进行编程计算,采用多维向量来表示回合战斗力指数计算过程。具体计算步骤如下:
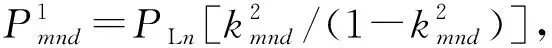
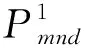
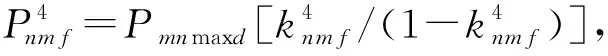
2.2 基于兵棋推演回合制的武器装备战斗力指数评估模型
回合制包含2层含义:1)交战双方必须按照顺序依次交替进行,己方的行动必须基于对方的行动结果,即按照对方战斗力最优原则,基于对方武器装备运用方案评估己方武器装备战斗力指数;2)根据对抗双方的作战规模确立推演粒度,即回合时间的长短,在战术级兵棋推演中通常为X(min)。
(2)
式中:T为回合时间;S为射速(发/s);w为毁伤概率;p为命中概率。
由此求得的1个回合时间内的动态战斗力指数在概念上与文献[9-11]中兰彻斯特方程的α、β是一致的。设x0为红方初始战斗力值,x(t)为对抗中红方t时刻的战斗力值;y0为蓝方初始战斗力值,y(t)为对抗中蓝方t时刻的战斗力值;α为蓝方单个作战单元对红方作战单元在单位时间内的损耗系数,β为红方单个作战单元对蓝方作战单元在单位时间内的损耗系数。则
(3)
如:假设T72与T62的对抗动态战斗力指数分别为600、200,即1辆T72相当于3辆T62;1个回合时间内发射的弹药发数与有效发数的比值为3,则T72与T62的回合对抗动态战斗力指数分别为1 800/回合、600/回合;1 800/回合意味着1辆T72具有在1个回合时间内消灭9辆T62的能力。
3 算例分析
笔者采用文献[1]中的计算数据,设红方、蓝方各有3种武器装备参与对抗,红方的综合战斗力指数分别为PH1=200,PH2=300,PH3=20;蓝方的综合战斗力指数分别为PL1=100,PL2=400,PL3=10;红方、蓝方的武器装备分别可使用3种弹药。各种武器装备使用不同弹药对抗时的损失交换比如表1所示。
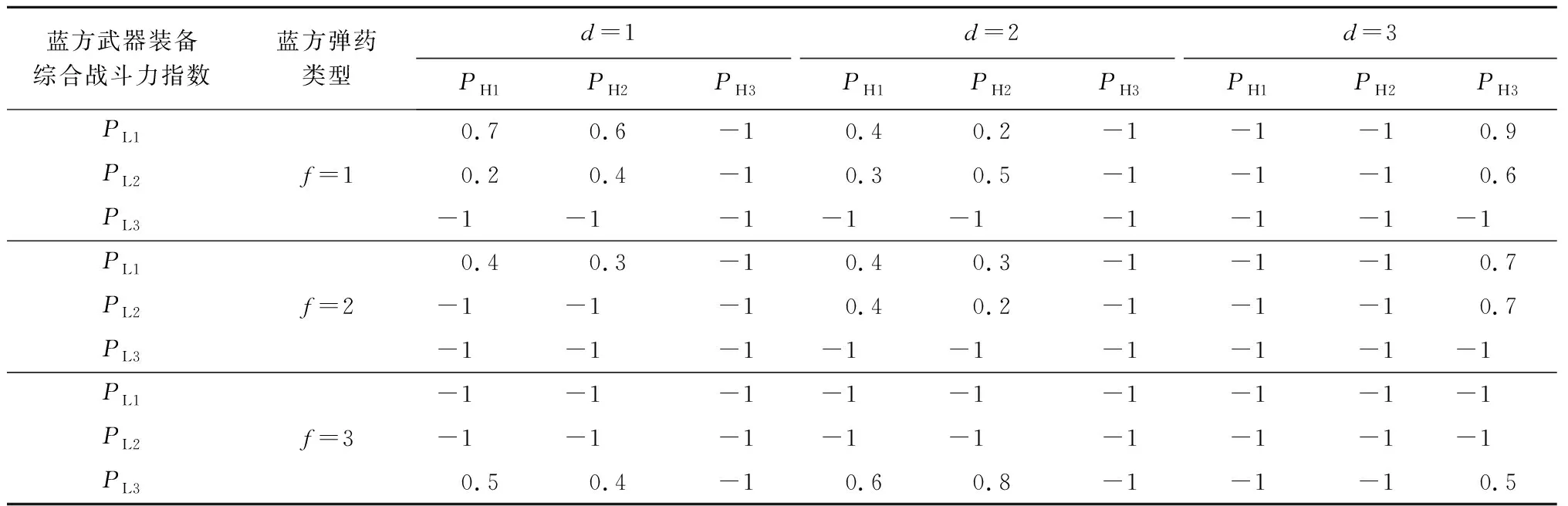
表1 红、蓝双方武器装备分别使用3种弹药时的对抗损失交换比
3.1 武器装备战斗力指数计算
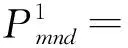
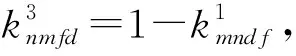
同理,可得其他武器装备的战斗力指数。蓝方武器装备使用3种弹药时的动态战斗力指数如表3所示,其中,dmin为给定蓝方武器装备、弹药类型,红、蓝双方武器装备对抗损失交换比最小时所对应的红方弹药类型,此处dmin对应d=1。

表2 红方武器装备使用3种弹药时的动态战斗力指数

表3 蓝方武器装备使用3种弹药时的动态战斗力指数
3.2 武器装备回合战斗力指数计算
红方武器装备使用3种弹药在1个回合时间内的射弹发数及摧毁蓝方目标装备所需的有效射弹发数如表4所示。
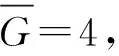
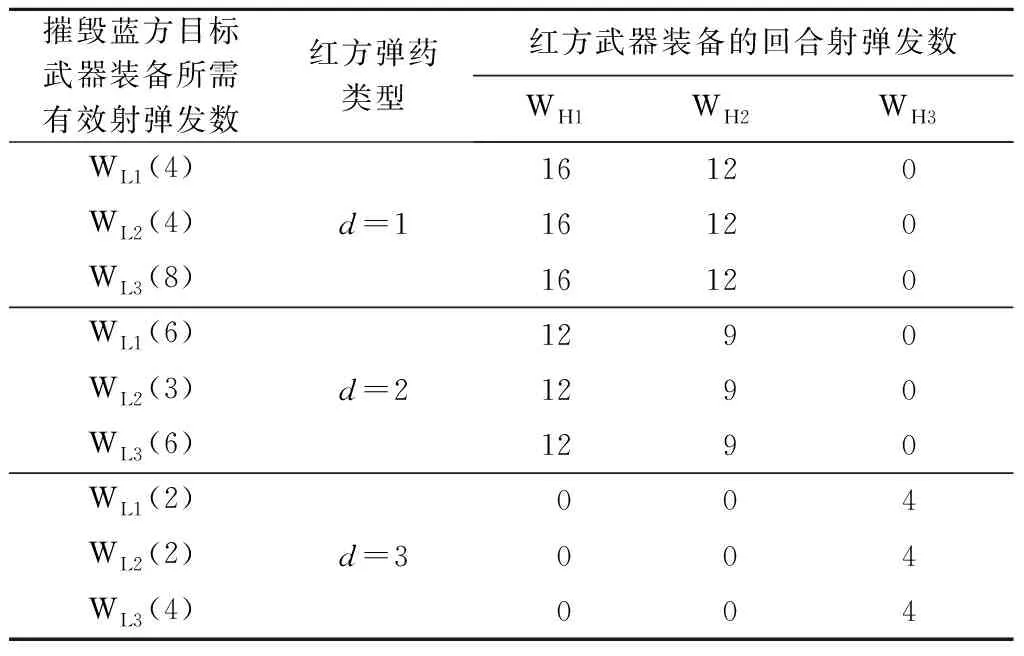
表4 红方在1个回合时间内使用3种弹药时的射弹发数及摧毁蓝方目标装备所需的有效射弹发数
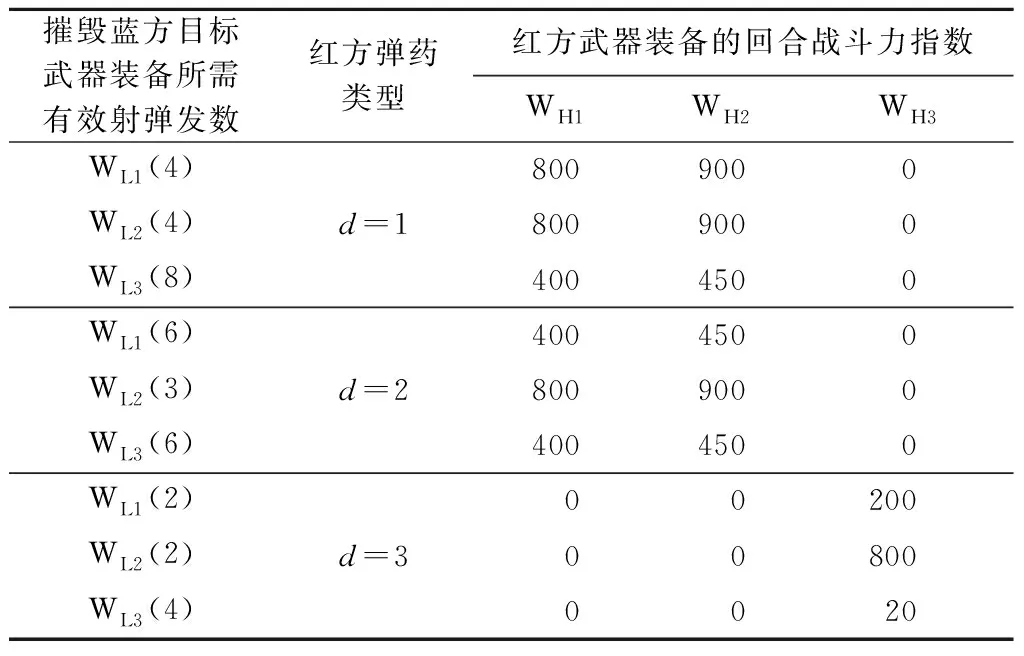
表5 红方武器装备使用3种弹药时的回合战斗力指数
由此可见:红方武器装备WH1采用弹药d1攻击蓝方目标武器装备WL1时的战斗力指数PH1=200,蓝方武器装备WL1采用弹药f1攻击红方目标武器装备WH1时的战斗力指数PL1=85.71,不再是以往一成不变的战斗静力值,并随着对方作战力量编成的变化而进行动态调整。
算例结果表明:相较于传统的战斗静力评估方法,基于武器装备对抗的损失交换比武器装备回合战斗力指数评估方法按照敌方战斗力最优原则,考虑双方实际交战态势,其评估结果较为保守,更接近真实值,更为合理有效,利用该值计算作战持续时间、双方的胜负概率以及预测双方作战实力随时间的变化情况将更接近实际战争规律,且使制订的作战方案更为科学、合理。
4 结论
笔者基于武器装备对抗的损失交换比,采用装备-弹药-目标方法,结合兵棋推演的回合制思路,按照“预已从严,料敌从宽”的基本原则,实现了武器装备回合战斗力指数的动态评估,该方法更加准确、合理,也更能体现武器装备的对抗性和博弈性,使武器装备战斗活力得以充分地体现,研究结果可为开展对抗双方的胜负概率、作战进程与时间的关系、武器装备保障需求研究等奠定基础。由于战争过程存在很大的不确定性,在实际对抗中武器装备未必会按照笔者提出的战斗力最优原则攻击最合适的目标,若仍然采用最优的战斗力指数来评估对抗双方的胜负概率、计算作战进程等,则会造成一定程度的失真,下一步将重点研究武器装备对抗中战斗活力的随机性。

