具有不确定项的随机非完整系统的自适应控制问题研究

鞠桂玲， 杜 健， 顾 娟, 单彩虹

(陆军装甲兵学院基础部， 北京 100072)

非完整系统产生于带有非完整或不可积约束机械系统的控制问题，如轮式机器人、车载倒立摆、欠驱动水下船舶等力学系统都可以归结为非完整系统。近年来，非完整系统的镇定问题得到了国内外研究者的广泛关注[1-4]。然而，目前考虑系统中随机性因素干扰的文献相对较少，但关于随机非完整系统的控制问题已得到了一些结果,如：WU等[5]考虑了一个三阶非完整系统的控制问题;文献[6-7]的作者考虑了x0-子系统带有随机性干扰的非完整系统的控制问题，但没有考虑x0-子系统包含未知参数的情形，且文献[7]中的不确定项需要满足线性增长条件。因此，笔者以文献[7]的模型为基础，综合考虑x0-子系统受非线性随机因素影响及包含未知参数的情形，通过综合运用文献[8-9]的参数分离技术、不等式放缩法与反推法，对一类具有非线性不确定项的随机非完整系统的自适应控制问题进行研究。

1 问题提出

考虑如下具有非线性不确定项的随机非完整系统：

(1)

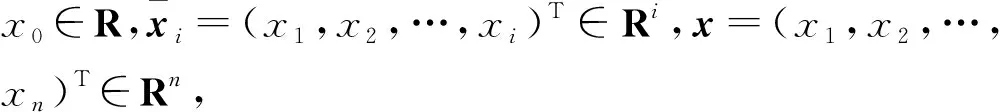
成立。

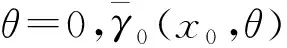
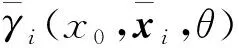
成立。

假设1、2表明原点是系统(1)的平衡点。实际系统中很多的不确定因素满足该假设[2-3]。

假设3：对于任意的0≤i≤n，存在已知的正常数λi和μi，使得未知的方向参数di(t)满足不等式

0<λi≤di(t)≤μi。

2 控制器的设计

控制器设计过程中用到如下3个引理。

引理1(参数分离技术)[8]:对于任意的连续函数f(x,y)，其中x∈Rm,y∈Rn,存在光滑函数a(x)≥1和b(y)≥1,使得不等式

|f(x,y)|≤a(x)b(y)

成立。

引理2(不等式放缩法)[9]:假设x和y是2个实变量，对于任意的正整数m、n和任意的正实数ε，使得不等式

成立。

定义1[5]：考虑随机非线性系统

dx=f(x,u)dt+gT(x)dω，

(2)

定义C2函数V(x)沿系统(2)的微分算子为

LV(x)

引理3[5]：考虑随机非线性系统(2)，若存在一个C2函数V(x):D→R+，满足

(3)

则系统(2)的解x=0依概率全局渐近稳定。式中：α1(·)和α2(·)为K类函数；α3(·)为非负光滑函数。

为了处理系统(1)固有的三角结构，分2个阶段分别设计控制器u0和u，以使得x0和x-子系统的状态依概率渐近稳定。

2.1 控制器u0的设计

由引理1可知：存在光滑函数γ0(x0)≥1和未知参数Θ0≥1，使得不等式

(4)

成立。

取李亚普诺夫函数

(5)

(6)

(7)

(8)

根据式(2)、(4)、(5)，可得

(9)

由式(9)可知：在式(7)的控制器作用下，x0-子系统依概率渐近稳定，且只要初始状态x0(t0)≠0，则有x0(t)≠0(t≥t0，其中t0为系统的初始时刻)。

2.2 控制器u的设计

2.2.1 系统坐标转换

当初值x0(t0)≠0时，引入状态-输入坐标转换

(10)

根据式(10)，式(1)中的xi-子系统转化为

(11)

式中：

f0(x0,θ))；

由假设2及引理1可知：对于任意的1≤i≤n, 存在光滑非负函数γi(·)、ξi(·)、ci(θ)和ei(θ)满足

(12)

2.2.2 控制器u的设计步骤

采用反推法对控制器u进行设计，其步骤如下：

步骤1： 取光滑虚拟控制器α1，定义误差变量ε1=y1,ε2=y2-α1,及李亚普诺夫函数

(13)

dε1=d1(t)y2dt+φ1(·)dt+φ1(·)dω，

(14)

由式(12)-(14)可得

LV1(·)= LV0(·)+ε1(d1(t)y2+φ1(·))+

(15)

取虚拟控制函数

(16)

将式(16)代入式(15)，可得

(17)

步骤i：假设在第i-1步中，存在虚拟控制律αi-1和误差变量εi，使得

(18)

成立。

取李亚普诺夫函数

(19)

式中：

对εi求导，由It微分公式可得

(20)

式中：

根据式(18)、(20)，可得

di(t)εiαi(·)+εiFi(·)+

(21)

由引理1、2，可得

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

式中：

均为待定的光滑函数。

由式(21)- (29)，可得

(30)

式中：

取虚拟控制函数

(31)

将式(31)代入式(30)，可得

(32)

步骤n：选取李亚普诺夫函数

(33)

式中:εn=yn-u，为误差变量。

通过与步骤i类似的推导，可得

(34)

选取控制器及参数估计量

(35)

(36)

将式(35)、(36)代入式(34)，可得

(37)

由引理3及式(37)可知：y-子系统依概率全局渐近稳定。结合坐标变换式(10)可知：系统(1)是依概率全局渐近稳定的。

3 切换控制策略及其主要结果

当初值x0(t0)≠0时，已针对系统(1)分别给出了控制器(7)、(35)。由式(7)、(8)可知，此时u0=0，坐标变换的分母为0。因此，不能采用控制器(5)、(35)。此时，设计控制器

(38)

定理：在假设1-3下，当t≤t*时采用控制器(38)，当t>t*时切换到控制器(5)，并通过反推法分别给出这2个时间段的控制器u，将其运用于系统(1)，这样对于任意初始值，闭环系统的状态依概率全局渐近收敛于0。

4 仿真实例

考虑下列非完整系统：

(39)

闭环系统的状态曲线和控制输入曲线分别如图1、2所示。可以看出：系统的状态和控制输入曲线均趋向于0,验证了本文所设计的控制器的有效性。

5 结论

针对x0-子系统具有不确定项干扰的一类新的随机非完整系统，笔者在考虑了系统中所具有的不确定因素的基础上，综合运用参数分离技术和反推法，设计了系统的自适应反馈控制器。同时，为了避免x0初值为0时，发生有限时间逃逸现象，设计了一种基于x0值的切换控制策略，该控制器使得闭环系统的状态依概率全局渐近收敛于0，通过仿真实例验证了该方法的有效性。

与文献[7]的模型相比，本文所建立的模型中，x0-子系统的不确定干扰项不需要满足线性条件，因此本文模型更具一般性，能更好地反映实际问题中存在的不确定干扰因素多属于非线性函数的情况，是随机非完整系统新的研究方向，而文献[7]的模型可看作本文的一个特例。然而，笔者未考虑实际中存在的时滞情况。下一步，将对具有随机不确定性的时滞非完整系统的控制问题进行研究。