螺旋驱动式管内机器人越障性能优化设计

李 特， 张 嘉 礼， 李 斌， 王 永 青

(1.大连理工大学 精密与特种加工教育部重点实验室， 辽宁 大连 116024；2.中国科学院沈阳自动化研究所 机器人学国家重点实验室， 辽宁 沈阳 110016 )

0 引 言

管道应用已经有上百年的历史，时至今日，各种类别的管道网络依然是石油、天然气、工业原料、废料、自来水等流体物质的主要运输手段.管道网络带来便利的同时，也给人类、环境带来了灾难.由于年久失修等自然或人为原因，管道爆炸、泄漏事故频发.管道故障的安全、高效检测方法一直是困扰工程师的难题.近年来，随着机器人技术的快速发展，学者们也开发了多种类型的管内检测机器人.最早出现的PIG式管内机器人[1]无主动驱动装置，仅依靠管内介质压差实现运动.主动轮式机器人一般辅助磁轮[2]或弹性支撑机构[3-4]，具有较好的管内运动能力.履带式机器人[5]具有较好的牵引能力，但是传动效率较差.螺旋驱动式机器人[6]也是一种轮式机器人，以传动机构简单(仅需要一个电机驱动)、运动效率高为特点.此外，还出现了多种基于仿生原理设计的管内机器人.例如，蠕动式机器人[7]是依靠前后两个腔囊的交替收缩与膨胀实现运动的，其移动速度较慢.仿蛇式机器人[8]模仿蛇类身体的蜿蜒扭摆，与管道内壁发生力的交互作用，从而实现运动.腿式机器人[9]仿生多足类动物，其机构与控制十分复杂.从传动机构和控制复杂性评价，螺旋驱动式管内机器人具有运动效率高、传动机制简单等特点，在中小管径管道检测中具有广泛应用前景[10].

管内机器人一般需要具备一定的越障能力，以克服潜在的环境障碍.在实际工程应用中，由于当前管道连接技术的限制，在两段管道接汇处会出现凸起或凹槽，从而成为机器人行进中的障碍，在后文的分析中，分别称为环形凸台障碍和环形凹槽障碍.虽然一般情况下障碍仅有几毫米高度，但是极有可能成为机器人不可逾越的障碍.管内机器人越障时主要受到弹性支撑机构的反作用力，其越障过程受力动态变化、作用机制复杂.因此，深入分析、优化越障性能对于提升机器人的管内作业能力具有重要研究意义.刘星等[11]提出了一种由两组螺旋轮驱动的管道机器人，并对机器人在凸台管道环境下的越障能力进行了动力学分析.李庆凯等[12]设计并研制了三轴差动式管道机器人驱动单元，并对其越障能力等驱动特性进行了分析.殷奇会等[13]为提高管道机器人在恶劣管道工作环境中的生存能力，提出了一种管道机器人越障能力的计算方法.在此基础上，面对凸台和凹槽管内障碍环境，综合考虑机器人主动轮和从动轮的综合越障能力十分重要，且对机器人的结构设计具有指导作用.

本文以螺旋驱动式管内机器人为对象，深入分析其环形凸台和环形凹槽越障性能，构建螺旋轮和从动轮的准静态越障模型.以机器人牵引能力、驱动电机转矩等为约束条件，构建机器人综合越障性能数学模型.基于指数惯性权重改进粒子群算法，优化求解综合越障性能最优时的决策参数向量.最后，将优化结果应用于螺旋轮角差动式管内机器人样机的设计中，通过管内试验验证越障性能优化方法的有效性.

1 准静态越障模型

首先，介绍螺旋驱动式管内机器人的基本运动原理.然后，分别建立螺旋轮、从动轮在环形凸台障碍和环形凹槽障碍中的准静态越障模型.

1.1 螺旋驱动式管内机器人运动原理

通过传动转换机构和螺旋轮将主驱动电机的轴向旋转运动转换为轴向直线运动是螺旋驱动的基本原理.机器人的螺旋轮在管道内壁形成螺旋线状运动轨迹，如螺栓在螺母中旋转推进一般.如图1所示，螺旋驱动式管内机器人[14]一般由旋转体、保持体、弹性支撑臂组成.保持体内部安装主驱动电机，经过减速器、联轴器传递动力，驱动旋转体整体旋转.保持体和旋转体上一般安装3组或4组周向均匀分布的弹性支撑臂，以保证机器人在水平、竖直放置的管道内部始终保持姿态、受力和运动的稳定性.

图1 螺旋驱动式管内机器人结构图

受弹性支撑臂弹力作用，螺旋轮与管道内壁之间产生压力，并借助法向静摩擦力，将主驱动电机转矩转换为轴向驱动力.静力平衡关系满足以下关系式[15]：

(1)

F=nfnicosα

(2)

式中：F为机器人轴向牵引力，τ为主驱动电机输出转矩，it为总传动比，R为管道内径，n为弹性支撑臂数量，fni为法向摩擦力，α为螺旋轮倾斜角.

1.2 环形凸台越障模型

环形凸台障碍一般是由电、气焊连接技术在两管道连接处产生的，尤其管道内侧常常会留下难以打磨的毛刺，从而形成凸台状障碍.

如图2所示，面对环形凸台障碍时，机器人螺旋轮或从动轮同时接触障碍边缘并挤压弹性支撑臂，直至滚轮爬过凸台障碍.在越障过程中，机器人的重心位置可认为保持不变.因此，在分析中仅考虑弹性支撑臂的弹力影响，而忽略机器人自身重力.

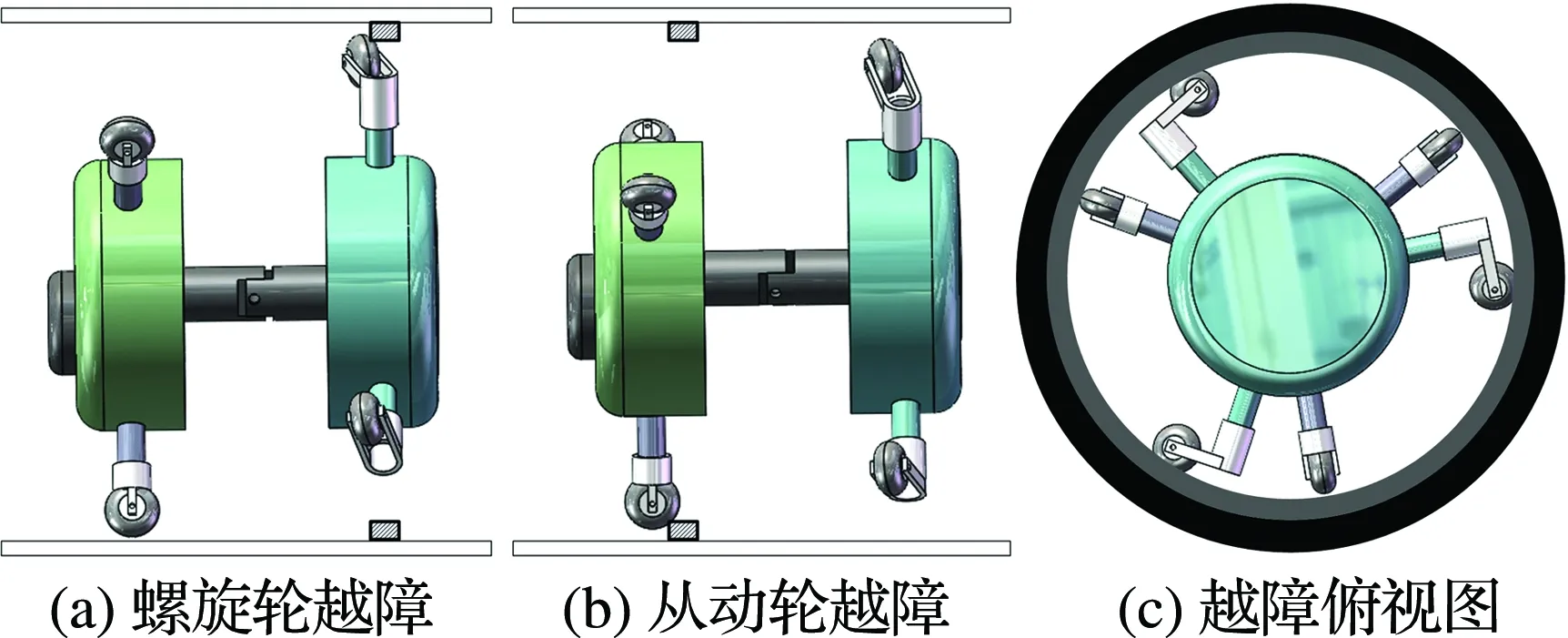
图2 机器人跨越环形凸台障碍

1.2.1 螺旋轮越障模型 首先分析机器人螺旋轮的环形凸台越障运动.假设旋转体上共配置n个弹性支撑臂，并以其中弹性支撑臂i的受力模型为例，建立管内机器人环形凸台越障模型，如图3所示.h表示环形凸台的凸起高度，h1表示机器人螺旋轮与管道内壁之间的垂直抬起高度.在螺旋轮与障碍物接触时，接触边缘点对螺旋轮有支持力Ni.Fti表示机器人越过障碍所需的牵引力，该力实际上是一个虚拟力，由螺旋驱动机构转换产生.Fli是弹性支撑臂中弹簧被压缩所产生的弹力，该力阻碍机器人跨越障碍.螺旋轮半径为rw，螺旋轮的倾斜角为αi.

图3 螺旋轮环形凸台越障受力分析

机器人越障速度缓慢，可以认为是一个准静态过程.因此，以边缘接触点为准静态平衡点，弹力Fli以Lr为力臂形成阻力矩Mr，牵引力Fti以Lp为力臂形成动力矩Mp.机器人成功越障必须满足以下约束条件：

Mp=FtiLp≥Mr=FliLr

(3)

即Fti产生的绕接触点动力矩必须大于Fli产生的阻力矩.Fti、Fli、Lp及Lr分别为

(4)

Fli=F0+kh1

(5)

Lp=rw+h1-h

(6)

(7)

其中k是弹性支撑臂内部的弹簧刚度系数，F0是弹簧预载力.

机器人越障所需的牵引力与螺旋轮和管道内壁之间的法向静摩擦力有关，而法向静摩擦力与螺旋轮和管道内壁之间的压力有关.如图4所示，根据几何和受力关系，凸台障碍对螺旋轮的支持力Ni为对应弹性支撑臂i的弹力在OA方向的分力.在△OAB中，根据勾股定理可得线段OA长度为

(8)

根据三角形相似原理可以得到Ni：

(9)

法向最大静摩擦力fn,max为

fn,max=μNi

(10)

图4 正压力分析

机器人越障成功应该保证法向静摩擦力fni不超过最大法向静摩擦力fn,max，必须满足如下约束关系：

(11)

机器人螺旋轮越障时，在保证螺旋轮不打滑和电机不过载的前提下，所能提供的最大电机输出转矩为

(12)

1.2.2 从动轮越障模型 从动轮越障受力关系如图5所示，与螺旋轮越障模型相似，机器人从动轮跨越障碍的动力矩Mdp和阻力矩Mdr也必须满足以下约束关系：

Mdp=FdtiLdp≥Mdr=FdliLdr

(13)

其中

(14)

Fdli=F0+khd1

(15)

Ldp=rw+hd1-hd

(16)

(17)

当从动轮越障时，螺旋轮一般处于正常管道环境内.螺旋轮与管道内壁之间的稳定作用力支撑了机器人从动轮的顺利越障.最大静摩擦力为

fdn,max=μF0

(18)

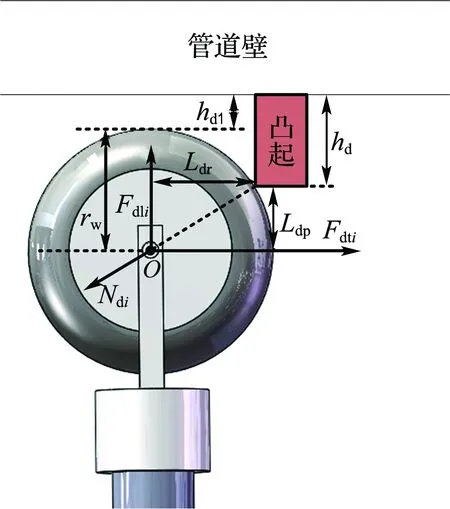
图5 从动轮环形凸台越障受力分析

螺旋轮摩擦力满足力约束关系：

(19)

机器人从动轮越障时，在保证螺旋轮不打滑和电机不过载的前提下，所能提供的最大电机输出转矩为

(20)

在判断机器人环形凸台越障高度时，需要分别判断螺旋轮和从动轮的越障能力.让电机以转矩τ依据式(12)和(20)输出，那么如果始终满足式(3)和(13)，则机器人能够实现越障.

1.3 环形凹槽越障模型

承接口连接是用于两管道结合的另一种常用技术.承插连接无法保证管道间严丝合缝，一般会形成环状凹槽缝隙，从而成为管内机器人的障碍.如图6所示，机器人跨越凹槽障碍时，经过陷入凹槽再爬越的过程.

机器人环形凹槽越障模型的建模方法与环形凸台越障类似，在此仅简单给出模型公式.如图7所示，机器人牵引力产生的绕接触点的动力矩不小于弹簧弹力产生的阻力矩时，才能成功越障，因此必须满足以下条件：

Fti(rw+h1-h)≥

(21)

虽然式(21)和式(3)具有相同的表达形式，但机器人牵引力和弹性支撑臂弹力的表达式并不相同，其分别表示为

(22)

Fli=F0+k(h1-h)

(23)

图6 机器人跨越环形凹槽障碍

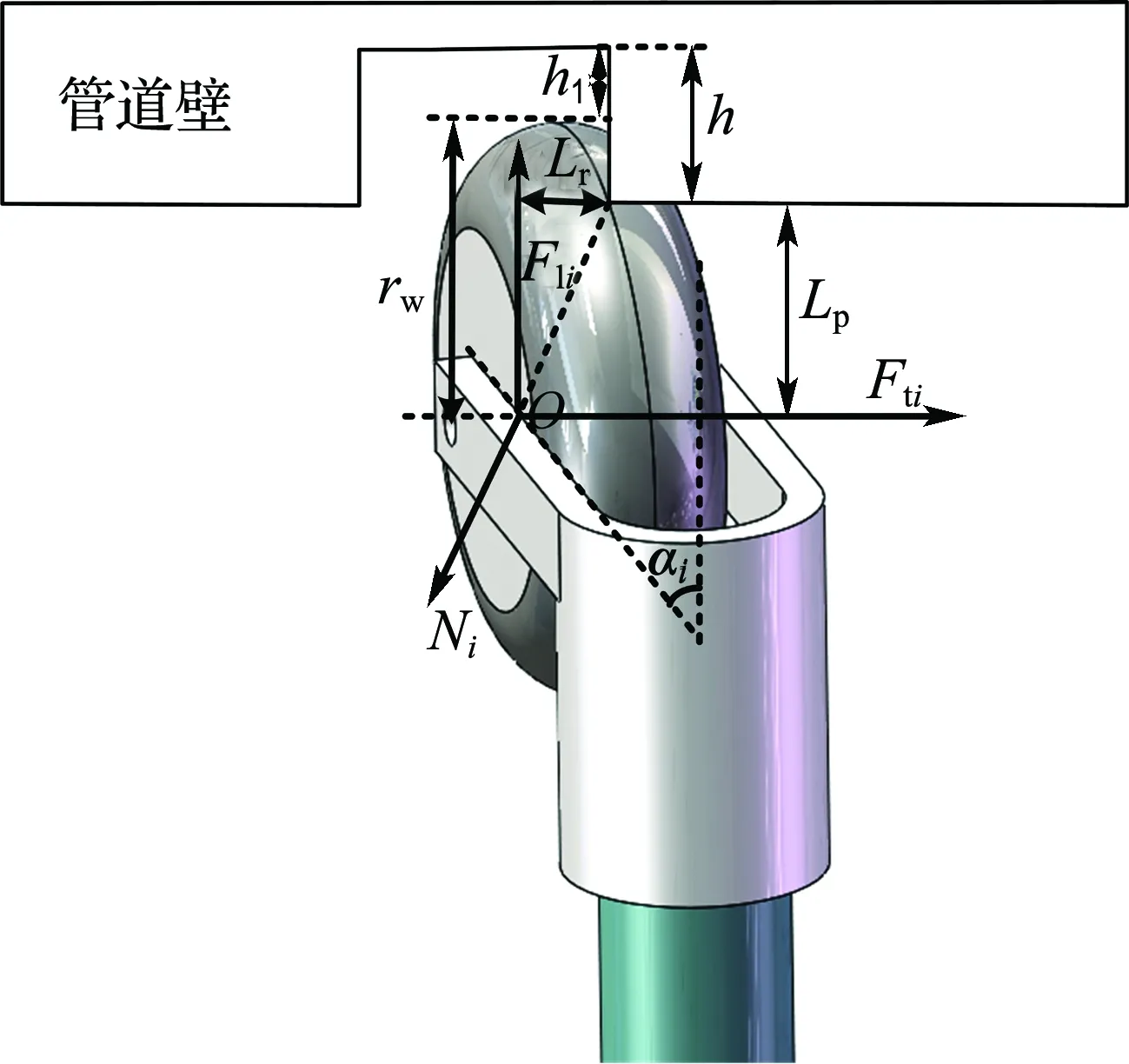
图7 螺旋轮环形凹槽越障受力分析

根据几何和受力关系，同样可以得到凹槽障碍对滚轮的支持力：

(24)

法向静摩擦力满足约束：

(25)

在保证滚轮不打滑和电机不过载的前提下，机器人跨越凹槽障碍时所能提供的最大电机输出转矩为

τ=min (τe,nfn,maxRcosαi/it)

(26)

从动轮的环形凹槽越障模型的建模过程与1.2.2节类似，其具体分析不再复赘，仅给出表达式发生变化的关键模型公式.式(15)表达式变为

Fdli=F0+k(hd1-hd)

(27)

2 越障性能优化方法

受到本体质量、设计几何尺寸及牵引力指标等约束条件影响，机器人的相关参数设计存在一定约束.将机器人综合越障性能最优的参数设计问题转化为多目标优化问题，并采用加权求和法将多目标问题转换为单目标优化问题.基于改进粒子群算法对优化数学模型求解，得到最优参数向量.

2.1 优化数学模型构建

一般地，将n维决策变量、m维子目标函数的多目标优化问题表示为[16]

miny=F(x)=(f1(x),f2(x),…,fm(x))

(28)

约束条件为

(29)

式中：x为n维的决策空间；y为m维的目标空间；F(x)为目标函数；g和h分别定义了多目标优化问题的q个不等式约束条件和p个等式约束条件；xmax和xmin为向量搜索的上下限.

依据越障模型，螺旋驱动式管内机器人面对环形凸台和环形凹槽障碍的越障性能与主驱动电机的额定输出转矩τe、弹性支撑臂内部弹簧的刚度系数k、预载力F0及螺旋轮半径rw有关.因此，参数决策空间向量为

X=(τekF0rw)T

(30)

约束条件是根据管内机器人设计要求、工程实现可能性所提出的设计变量可行域约束.恰当的可行域约束有利于减小最优解的搜索范围并提高搜索效率.通常，电机额定转矩越大，其质量也越大，因此，受质量限制设定额定转矩上限约束条件.机器人需要具备一定牵引能力，以克服摩擦等阻力，因此，设定牵引力下限.受机器人设计尺寸、轴承型号等限制，螺旋轮的半径不能过大，也不能过小，因此设定双向边界约束.约束条件表示如下：

τe≤τe,max

(31)

Ft≥Ft,min

(32)

rw,min≤rw≤rw,max

(33)

子目标函数包含环形凸台越障高度函数和环形凹槽越障高度函数，并将其表示为

(34)

(35)

其中H1、H2分别表示环形凸台和环形凹槽越障高度.

采用加权求和法将多目标优化问题转换为单目标优化问题求解.因此，优化数学模型转换为

minF(X)=w1f1(X)+w2f2(X)

(36)

其中w1和w2是权重值，且w1+w2=1.

2.2 基于改进粒子群算法的模型优化求解

粒子群优化算法是Kennedy和Eberhart[17]提出的一种群体智能算法，其核心思想来源于鸟群的觅食行为及其信息共享机制.设群体规模为N，则第i(i=1,2,…,N)个粒子的位置向量可以用xi表示，其个体最优位置向量记为pbest，速度向量为vi，群体全局最优位置向量为gbest.标准粒子群算法的基本模型表示如下：

速度更新公式：

vi(t+1)=wvi(t)+c1r1(t)(pbest(t)-xi(t))+

c2r2(t)(gbest(t)-xi(t))

(37)

位置更新公式：

xi(t+1)=xi(t)+vi(t+1)

(38)

式中：t表示进化迭代的次数，w表示惯性权重，c1和c2是学习因子，r1和r2表示均匀分布在(0,1)的随机数.

为了提高算法收敛速度，采用基于指数惯性权重调整策略的改进粒子群算法[18].式(37)中的惯性权重w改为

(39)

式中：w0为惯性权重初值，g为当前进化代数，G为最大迭代代数，a为局部搜索吸引子，b为全局搜索吸引子.

约束条件的处理是优化方法的关键.采用罚函数法处理约束.该方法对满足约束条件的粒子不作处理，对不满足约束条件粒子的函数值给予“惩罚”，使其在进化中落后而不被选中，其基本表达式为

(40)

其中F(X)代表种群粒子函数值，P(X)代表惩罚函数值，Fnew(X)表示修正后的新函数值.

如图8所示，是基于粒子群优化算法求解最优决策参数向量X的方法流程图.首选，选定优化模型的约束条件等基本参数，进行粒子种群的初始化，包括规模、粒子位置、速度等.然后，设定迭代次数，并以其为终止条件.在迭代周期内，计算每个粒子的函数值，其计算方法在后文给出.选出粒子最优位置pbest及全局最优位置gbest，并利用粒子群算法的基本公式更新其速度vi(t+1)和位置xi(t+1).最后，在达到迭代次数上限后，选择全局最优粒子所对应的参数作为越障综合性能最优的参数向量.

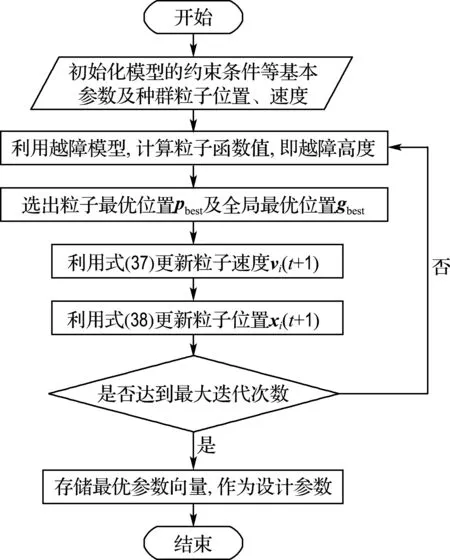
图8 优化方法流程图

粒子函数值即当前参数向量下机器人的越障高度.利用前面所提越障模型，基于迭代思路，提出越障高度的解算方法.环形凸台越障高度H1和环形凹槽越障高度H2，分别指其螺旋轮和从动轮共同所能跨越的最大凸台/凹槽高度.其计算方法的伪代码如下.

%以螺旋轮凸台越障为例的伪代码：

初始化越障高度h

flag=1;

flag1=0;

flag2=0;

while(flag==1)

forh1=0:0.01:h%爬升高度步进0.01 mm

利用式(12)，计算τ;

利用式(4)～(7)计算Fti，Fli，Lp，Lr;

flag2=0;

ifMp

flag1=1; %该高度下越障失败

break;

else

flag2=1; %当前位置可翻越

end;

ifflag1==1

flag1=0;

flag=0;

ifflag2==1

flag2=0;

h=h+0.1; %增加越障高度，步进0.1 mm

end;

h=h-0.1; %将上一迭代周期高度作为最终越障高度

3 试验验证

3.1 系统参数设计

为了验证所提越障性能优化方法，将其应用于螺旋轮角差动式管内机器人的设计中，并进行试验验证.其本体及运行环境基本参数如表1所示.针对内径为209 mm的目标管道进行设计，主驱动电机最大额定转矩限定为200 mN·m，牵引力指标设定为30 N.滚轮的最大、最小半径分别为11和8 mm.规定所有弹性支撑臂的内部弹簧具有相同参数.

表1 基本参数

利用改进粒子群算法求解最优参数，其基本参数见表2.

表2 改进粒子群算法参数

表3中显示的是经过优化求解得到的最优设计参数.相应的环形凸台越障高度、环形凹槽越障高度分别为2.1、2.7 mm.

表3 最优设计参数

如图9所示，螺旋轮角差动式管内机器人[19]是一种基于螺旋驱动原理并融合独特的螺旋轮角自适应联动机构的适用于直管、弯管运动机器人.该机器人由螺旋驱动机构、自适应联动机构、旋转弹性臂和支撑弹性臂组成.将优化结果应用于该机器人的设计中并进行试验验证.

图9 螺旋轮角差动式管内机器人

3.2 环形凸台越障试验

验证试验分别在具有焊接点的不锈钢管道和具有连接头的PVC管道内进行.管道内径皆为209 mm.首先，验证螺旋轮角差动式管内机器人的环形凸台越障能力，令其在具有环形凸台障碍的管道内运动.如图10所示，该管道是由两段直管和一个弯头焊接而成的.在两处管道接缝处，形成了很明显的凸台障碍，其平均高度约为2 mm.

图10 环形凸台越障试验管道

如图11所示，经过10次试验验证，结果表明：依据优化结果设计的螺旋轮角差动式管内机器人的螺旋轮和从动轮都能够顺利跨越2 mm高的环形凸台障碍.

图11 机器人环形凸台越障试验

3.3 环形凹槽越障试验

如图12所示，为了验证机器人的环形凹槽越障能力，设计了由承插口方式连接的两段直管道.在管道连接处，形成了一个深度为2 mm的环形凹槽障碍.通过10次试验发现，机器人可以顺利通过障碍.

图12 机器人环形凹槽越障试验

4 结 语

本文重点分析了螺旋驱动式管内机器人的管内越障问题，针对管道内部典型的环形凸台障碍和环形凹槽障碍，分别构建了机器人螺旋轮和从动轮的准静态越障模型，获得了越障运动能力与机器人驱动力矩、管道摩擦因数等变量的力学关系.在此基础上，构建了综合越障性能数学模型，并基于改进粒子群算法对螺旋驱动式管内机器人的驱动力矩、弹簧刚度系数等设计变量进行了优化求解.试验结果表明：依据优化结果设计的螺旋轮角差动式管内机器人的螺旋轮和从动轮都能够顺利跨越2 mm高的环形凸台/凹槽障碍.