基于信息集成算子的舰船舱室设计方案评估

李 晓 文， 朱 兆 一*， 熊 云 峰， 袁 红 莉， 扈 喆

(1.集美大学 轮机工程学院， 福建 厦门 361021；2.福建省船舶与海洋工程重点实验室， 福建 厦门 361021 )

0 引 言

新世纪海军舰船系统日益复杂，越来越多的高科技武器装备上舰使得船内空间更加狭小，能否在有限的空间内妥善布置各类功能型舱室，使其最大限度地满足舰员与设备的需求，是评估舰船舱室设计方案优劣的重要指标之一.舰船作为典型且复杂的人-机-环境系统，其舱室设计方案评估要遵循人-机-环境系统工程学的基本原理，建立合理的舱室要素指标体系，这对发挥舰船能效、保证可靠性具有重要意义.由于舰船人-机-环境系统存在一系列具有模糊性的彼此关联的难以定量化、模型化的概念和要素，传统的依靠评估专家决策的方法也存在一定的主观性，因而在舱室设计之初，急需一套行之有效的客观科学的方案评估方法[1-2].

直觉多属性决策是当前评估决策领域的研究热点，在实际的工程决策中具有广泛的应用前景[3].Szmidt等[4]提出了直觉模糊数和少数服从多数的群决策方法.文献[5]定义了直觉模糊加权几何算子(IFWG)、直觉模糊有序加权几何算子(IFOWG)直觉模糊和混合几何算子(IFHG).文献[6]利用IFHG和IFWG给出了对应的群决策方法.文献[7]引入了多种直觉偏好关系，定义了直觉模糊算术平均算子(IFAA)和直觉模糊加权算术平均算子(IFWAA)，给出了基于相关算子的多属性群决策方法.上述方法很好地解决了事物的模糊多属性问题，但对属性关联和专家偏好交互等无法做出有效决策.Sugeno 提出模糊测度，在决策过程中同时考虑单个属性和属性集的权重，能有效处理关联多属性决策问题.基于直觉模糊数的多属性决策方法在处理不确定性信息时相比传统的模糊集有更强的表达力，决策方法更加灵活、科学，更适合用来处理现实中的各种问题[8-12].文献[13-14]应用Choquet 积分研究信息集成算子，并解决了关联多属性决策问题.文献[15]提出模糊数直觉模糊数集，弥补了直觉模糊数和区间直觉模糊数缺少重心的缺陷.

由于舰船舱室设计涉及船体、空气、振动、噪声等多个专业和学科，考虑到不同领域专家的偏好特性以及多个属性间的关联特性，如果直接将差异较大的评价结果进行集结，将会影响评估决策的科学性与合理性.本文综合考虑舰船舱室设计过程中的各种利弊因素以及多种决策评估方法的适用特征后，基于模糊测度和Choquet积分，求解信息集成算子，建立舰船舱室设计方案评估流程，最终形成基于信息集成算子的舰船舱室设计方案评估方法，从而有效处理关联多属性决策问题，为舰船舱室设计方案评估提供一种可行、有效的新方法.

1 舱室设计方案评估属性指标建立

舰船舱室设计实质上是空间和环境的设计，在满足各项功能和特征的前提下，对整个舰船进行整体和局部的区域划分，为舰船上所有设备和舰员提供所需的空间，进而达到人-机-环境的综合协调，以实现舰船的作战使用性能.

舱室设计的主要目的之一是满足各级各部门舰员的需求，保证其良好的工作环境和生活质量，进而发挥其最大战斗力，最终提高舰船的作战效率.为了更好地实现不同舱室的功能，发挥舰船的最大效率，在舱室设计的过程中需要重点考虑以下属性和因素：舱内结构、交通路线、舱外配套设施、空间环境以及安全性等.以上各因素又涉及许多不同的专业和学科要素，具体指标参见图1.

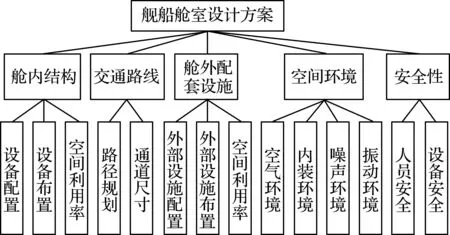
图1 舰船舱室设计评估指标体系

2 信息集成算子建立

2.1 模糊数直觉模糊数

1965年，Zadeh[10]提出了模糊集理论，可以描述外延不明的亦此亦彼的模糊概念，对经典集合进行了有效扩充.1986年，Atanassov[11]对Zadeh 理论进行拓展，通过研究新的属性参数(非隶属度函数)，得出直觉模糊集的概念，以此来描述非此非彼的模糊概念，能更好地处理舰船舱室设计评估等涉及属性要素众多的工程实际问题.其中，直觉模糊集的定义如下：

定义1[11]若存在任一已知论域X，则其上存在对应的直觉模糊集

A={〈x，μA(x)，νA(x)〉|x∈X}

(1)

其中μA(x)：X→[0，1]，νA(x)：X→[0，1]分别代表A的隶属度函数μA(x)和非隶属度函数νA(x)，并且对于A中所有x∈X，都有0≤μA(x)+νA(x)≤1成立.

刘锋等[16]提出了模糊数直觉模糊数集，如下所示：

E^={(xi,〈μ^E^(xi),ν^E^(xi)〉)|xi∈X}

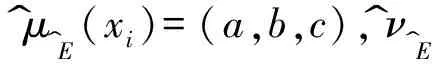
(2)

其中(xi)=(l，p，q)均为三角模糊数，a、b、c和l、p、q分别为隶属度和非隶属度的下界、重心和上界.

2.2 模糊测度

定义2[17]设P(X)为X={x1，x2，…，xn}的幂集，给定ρ∈(-1，∞)，μ：P(X)→[0，1]，若满足下列条件，则称μ为定义在X上的模糊测度：

(1)μ(∅)=0，μ(X)=1；

(2)假如B，C∈P(X)，B∩C=∅，则有μ(B)≤μ(C)；

(3)∀B，C∈P(X)，B∩C=∅，则有μ(B∪C)=μ(B)+μ(C)+ρμ(B)μ(C).

2.3 Choquet积分

定义3[12]若μ为定义在X={x1，x2，…，xn}上的模糊测度，αi(i=1，2，…，n)为X上一组模糊数直觉模糊数，则αi(i=1，2，…，n)关于模糊测度μ的离散Choquet积分定义为

(3)

式中：α(i)为αi的变换，使得α(1)≤α(2)≤…≤α(n)；A(i)={x(i)，x(i+1)，…，x(n)}，且A(n+1)={0}.

2.4 评价函数

式(4)所示为模糊数直觉模糊数的评价函数(也称得分函数)，通过它可以对其进行定量比较.设α=〈(a，b，c)，(l，p，q)〉为一个模糊数直觉模糊数，则称

(4)

为α的得分函数，其中S(α)∈[-1，1].S(α)的值随α的增大而增大.

若S(αi)(i=1，2，…，n)存在等值情况，则借助得分函数L(α)来比较，即

(5)

其中L(α)∈[-1，1]，L(α)值越大，α越大.

2.5 信息集成算子

设αi=〈(ai，bi，ci)，(li，pi，qi)〉(i=1，2，…，n)为一组模糊数直觉模糊数，μ为X的模糊测度，则信息集成算子的结果为模糊数直觉模糊数，并且存在

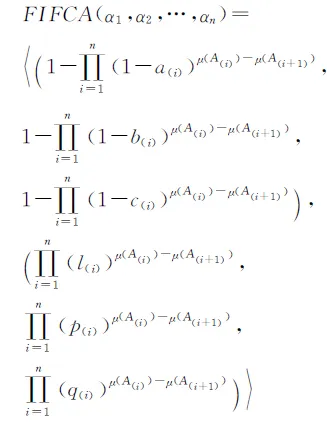
3 舱室设计方案评估

3.1 方案排序流程

舰船舱室设计方案评估属于多属性决策问题，评估结果既要反映舰船总体设计要求又要体现舰员的实际需求，本文基于信息集成算子进行舰船舱室设计方案的综合评估，具体分为以下5个步骤：

(1)综合备选方案，确定舰船舱室设计方案的评估指标体系(参见图1)，在此基础上建立舱室设计方案集合、属性集合和决策矩阵.

方案集合：

A={A1，A2，…，Am}；m≥2

属性集合：

X={x1，x2，…，xn}；n≥2

决策矩阵：

(2)依据2.4节评价函数的定义，对方案集合A中的每个方案进行初始排序.

(3)经专家评定，进行各个属性和属性集的模糊测度.

(4)基于信息集成算子获得决策矩阵针对每个方案的综合评价结果.

(5)通过上述(4)的评价结果，进行排序择优.

3.2 敏感性分析流程

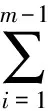
假设xj的敏感性系数是Mj，临界值是Dj.其中，Dj对应所有可行的最小相对变量的极小值；Mj与Dj互为倒数.

4 实际应用

将基于信息集成算子的多属性决策方法应用到实船舱室设计方案的评估筛选中，为了方便设计师和舰员的理解应用，便于对比研究，在保留关键因素的基础上，将应用实例缩小到某船的一个相对独立的生活区域，针对5套舱室设计方案A={A1，A2，A3，A4，A5}，3个属性指标——安全性x1、舱内配置x2、空间环境x3.处理3个属性指标所对应的评估信息，获得表1所示的用模糊数直觉模糊数来表示的决策矩阵.

基于前文的方案评估流程，进行设计实例的评估计算：

(1)基于具体情况和相关领域专家对多个属性和属性集的模糊测度，得到如下结果：

μ(∅)=0，μ({x1})=μ({x2})=0.5，μ({x3})=0.4，μ({x1，x3})=0.7，μ({x1，x2})=0.8，μ({x2，x3})=0.7，μ(X)=μ({x1，x2，x3})=1

(2)利用Choquet积分对5个舱室设计方案的模糊数直觉模糊数信息进行集成.其结果如下：

A1=〈(0.522，0.624，0.704)，(0，0.153，0.183)〉

A2=〈(0.472，0.572，0.634)，(0.100，0.200，

0.266)〉

A3=〈(0.613，0.638，0.741)，(0.115，0.153，

0.217)〉

表1 决策矩阵

A4=〈(0.494，0.578，0.631)，(0，0.152，0.200)〉

A5=〈(0.536，0.638，0.741)，(0，0.183，0.259)〉

(3)对上述信息集成结果进行得分评估，并排序择优.

评估结果如下：S(A1)=0.469，S(A2)=0.374，S(A3)=0.498，S(A4)=0.445，S(A5)=0.462.

优劣排序结果如下：A3>A1>A5>A4>A2.

基于评价函数的定义可知，最佳舱室设计方案为A3，与实际情况相符.

由于5个备选方案的评价结果无重复，仅通过一次评估计算即可确认最终结果，无须二次评判.由此可见，基于信息集成算子的舰船舱室设计方案评估方法较为准确、可靠.

为进一步验证该方法的科学性与合理性，应用经典的层次分析法和直觉模糊多属性决策方法对以上5个方案进行二次评估.

(1)基于层次分析法，建立以下层次结构模型，如图2所示.

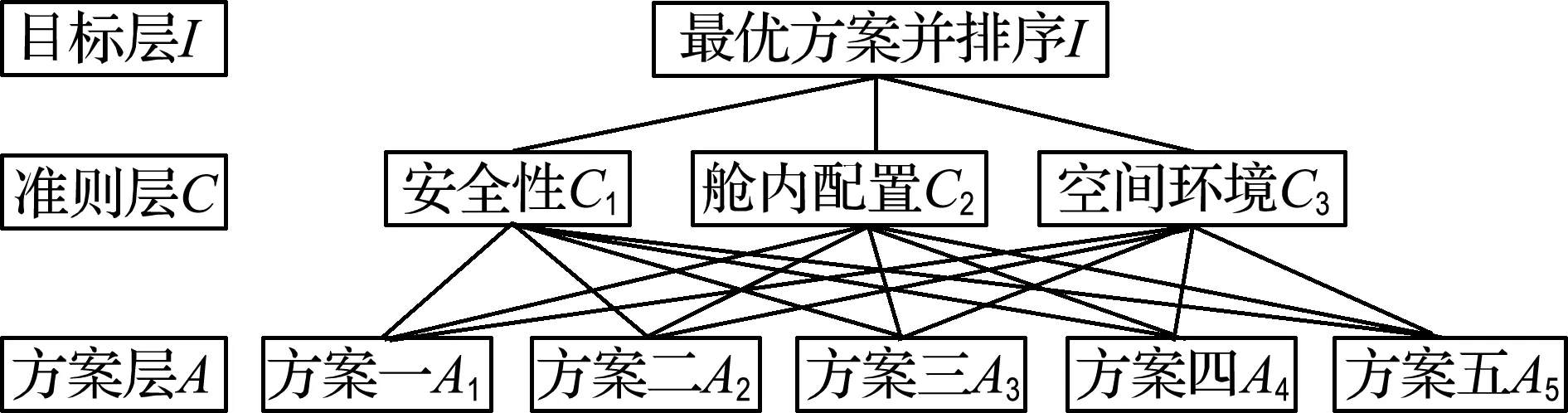
图2 舱室设计方案层次分析结构模型

为保证判断结果的一致性，由相同的决策者将5个舱室设计方案和3个准则，按层次分析法的特性进行排序，构造目标与准则之间以及准则与方案之间的判断矩阵，经过层次单排序、总排序以及一致性检验[18]，得出5个舱室设计方案的优劣以及最佳结果，如表2所示.多个方案的具体优劣顺序为A3>A1>A5>A4>A2.其中，一致性指标为0，随机一致性指标为0.58，随机一致性比率为0.

表2 方案层次排序值

(2)直觉模糊多属性决策过程中，为进一步确保本文方法结果的准确性，加入直觉模糊数算法进行对比，为保证参数值的一致性，采用本文决策者评价的重心值作为专家的评价矩阵，同时通过用户代表对5个方案进行评价并赋予属性权重，采用合取模型进行计算(详细算法参见文献[19])，具体结果参见表3，5个舱室设计方案的优劣顺序为A3>A1>A5>A4>A2.

表3 直觉模糊多属性决策评估量值

分析计算结果得出，3种方法的评估结果一致，但评估量值存在一定的不同，为做到更加直观清晰的对比，将上述结果转化为线图形式，参见图3.为方便曲线对比，将层次分析法的评估量值加0.1，做平移处理.

对比研究发现，图3中基于信息集成算子的多属性决策方法、直觉模糊多属性决策方法以及层次分析法的曲线走势大体一致，但备选方案的属性集存在关联，导致直觉模糊多属性决策方法和层次分析法的评估结果相对集中，分散性差，多个方案的优劣性不够突出，不易做出最终决策.尤其多个方案相似时，容易强化决策者的主观偏好和人为选择障碍.反观基于信息集成算子的多属性决策方法优劣明显，结果客观，工程适用性较好，因而其评估结果较其他两种方法更为科学合理.

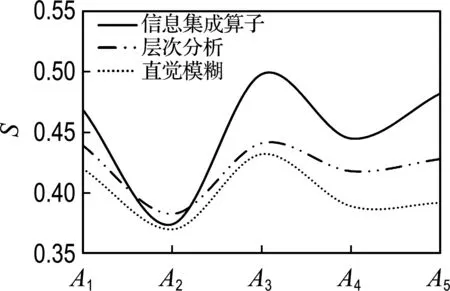
图3 评估曲线对比

为消除决策者对评估结果的影响，融入方案排序对权重变化的敏感性分析，基于上述3.2敏感性分析流程，计算出各属性对应权重变化的敏感性系数，详细算法参见文献[20]，具体结果参见表4.

表4 各属性权重变化的敏感性系数

敏感性系数越大，对应的临界值越小，方案排序对属性权重变化的敏感程度越高.可见，方案排序对敏感性系数越大/临界值越小的属性越敏感.

5 结 语

舰船舱室设计涉及多专业、多学科，并且要随总布置改变随时变更，因此舱室设计方案的评估是一个复杂烦琐的决策问题，需要简洁有效的方法来应对其复杂性和多样性.本文提出的基于模糊测度和Choquet积分的信息集成算子法，解决了存在关联的多属性决策问题，拓展了传统模糊决策方法的应用范围和准确性；同时弥补了基于直觉模糊数和区间直觉模糊数等决策方法存在的重心缺陷问题，提升决策效率.通过实例对比研究，验证了本文基于信息集成算子的舰船舱室设计方案评估方法的可靠性和准确性，并证明其具备较强分散性，对多种方案优劣区分度明显，较之传统的层次分析法和直觉模糊多属性决策方法能更为有效地对舰船的多种舱室设计方案进行择优决策.此外，本文方法也可以应用到其他复杂工业设计方案的评估决策中.