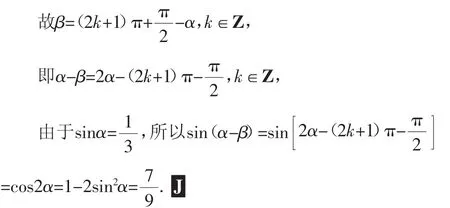一道三角求值题的多解与拓展

☉江苏省张家港市崇真中学 陈 斌

三角函数的求值问题一直是高考中常见的题型，2017年高考北京卷理第12题的三角求值问题，通过精妙的设计，把三角函数中角的推广、三角函数的定义、诱导公式以及三角恒等变换等相关知识巧妙地结合在一起，题小但量大.该题在解法上具有多样性，解题切入口也不唯一，这样能更好地考查学生思维的灵活性、多样性、拓展性.

【高考原题】（2017·北京理·12）在平面直角坐标xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称.

思维分析1：根据角α与角β的始边相同，终边关于y轴对称建立相应的关系式，通过角之间的运算，结合诱导公式、二倍角公式加以求解三角函数值问题.

解法1（对称角关系法1）：因为角α与角β的始边相同，终边关于y轴对称，则有α+β=（2k+1）π，k∈Z，

故β=（2k+1）π-α，k∈Z，即α-β=2α-（2k+1）π，k∈Z，

所以cos（α-β）=cos［2α-（2k+1）π］=-cos2α=2sin2α-

思维分析2：根据角α与角β的始边相同，终边关于y轴对称建立相应的关系式，通过关系式的转化与诱导公式，并结合两角差的余弦公式来求解三角函数值问题.

解法2（对称角关系法2）：因为角α与角β的始边相同，终边关于y轴对称，则有α+β=（2k+1）π，k∈Z，

故β=（2k+1）π-α，k∈Z，

则sinβ=sin［（2k+1）π-α］=sinα，cosβ=cos［（2k+1）πα］=-cosα，

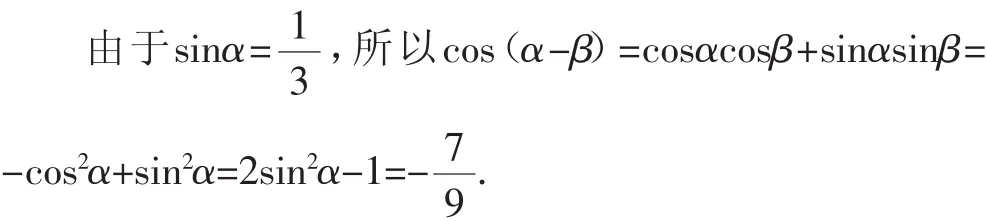
思维分析3：先在角α的终边上任取一点P（m，n）（n≠0），结合条件建立两参数之间的关系，结合对称的性质以及三角函数的定义求解相应的三角函数值，利用两角差的余弦公式加以求解三角函数值问题.

解法3（定义法）：在角α的终边上任取一点P（m，n）（n≠0），

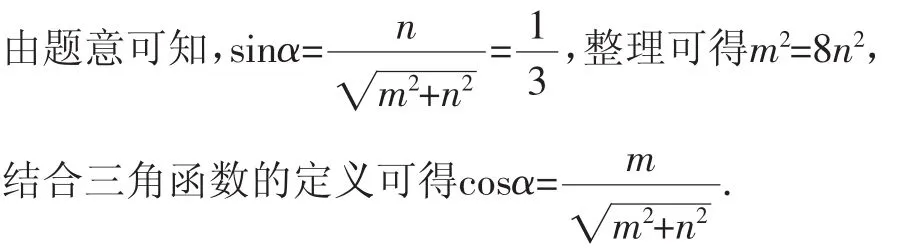
由于角α与角β的始边相同，终边关于y轴对称，则点Q（-m，n）在角β的终边上，由三角函数的定义可得

所以cos（α-β）=cosαcosβ+sinαsinβ

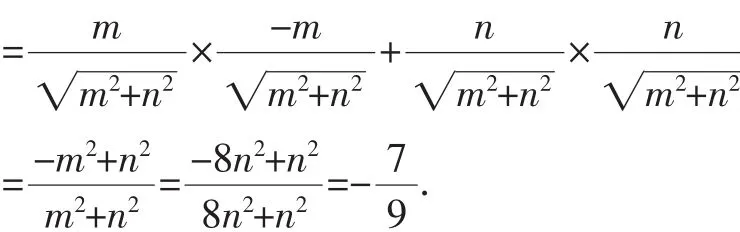
思维分析4：根据条件中角α的正弦值确定角α的终边所在的象限，通过分类讨论，选取相应象限内角α的终边上的特殊点，结合对称性质与三角函数定义来求解对应的三角函数值，再结合两角差的余弦公式来处理即可.

（1）当角α的终边在第一象限内时，可在角α的终边上取特殊点P（2，1），点P关于y轴的对称点为Q（-2，1），

【总结拓展】综合比较以上各解法，各有特色，各有所长.解法1与解法2直接找出两角之间的关系，然后利用诱导公式、三角恒等变换公式来求解三角函数值；解法3使用的是三角函数的定义，属于一般方法，回归定义；解法4根据角的三角函数值只与角的终边位置有关，而与点的选取无关，通过直接选取终边上的特殊点法，这样处理可以减少运算.其实，经过进一步分析，可以拓展以下一些具有一定创新性的问题.

变式方向一：条件简单化

【思维拓展1】（2017·北京文·9）在平面直角坐标xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称.

解析：因为角α与角β的始边相同，终边关于y轴对称，则有α+β=（2k+1）π，k∈Z，故β=（2k+1）π-α，k∈Z，

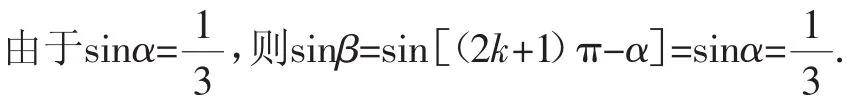
变式方向二：对称角度变化一

【思维拓展2】（原创）在平面直角坐标xOy中，角α与角β均以Ox为始边，它们的终边关于x轴对称.若sinα=

解析：因为角α与角β的始边相同，终边关于x轴对称，则有α+β=2kπ，k∈Z，

故β=2kπ-α，k∈Z，即α-β=2α-2kπ，k∈Z，

变式方向三：对称角度变化二

【思维拓展3】（原创）在平面直角坐标xOy中，角α与角β均以Ox为始边，它们的终边关于坐标原点对称.若

解析：因为角α与角β的始边相同，终边关于坐标原点对称，则有β-α=（2k+1）π，k∈Z，

故β=α+（2k+1）π，k∈Z，即α+β=2α+（2k+1）π，k∈Z，

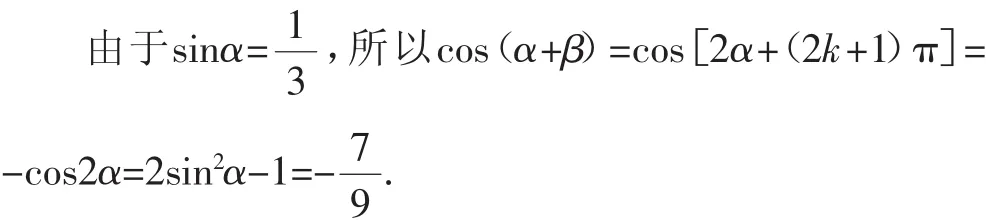
变式方向四：对称角度变化三

【思维拓展4】（原创）在平面直角坐标xOy中，角α与角β均以Ox为始边，它们的终边关于直线y=x对称.若

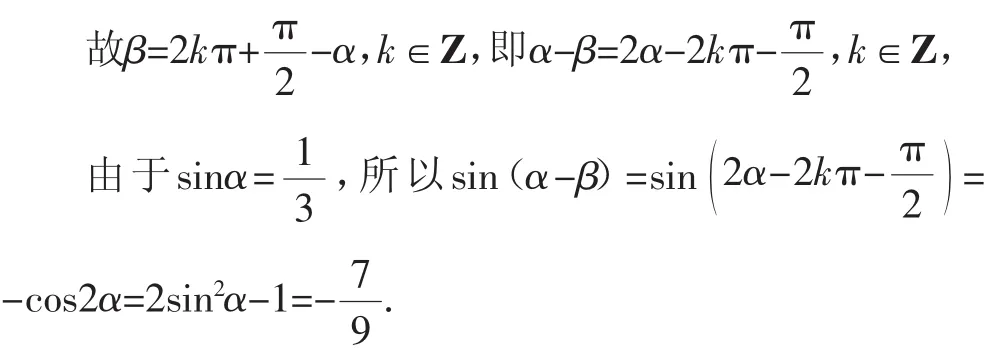
变式方向五：对称角度变化四

【思维拓展5】（原创）在平面直角坐标xOy中，角α与角β均以Ox为始边，它们的终边关于直线y=-x对称.若