高考数学文化类试题的几种类型

☉四川内江师范学院数学与信息科学学院 潘 超

☉新疆阿克苏地区新和县塔什艾日克乡中学 毛钟燕

《普通高中数学课程标准（2017年版）》的课程性质、基本理念、课程目标、课程结构、实施建议等模块中对“数学文化”都有明确的要求，强调要将数学文化融入课程内容和数学教学活动.通过在数学教育中渗透数学文化，让学生了解数学的发展历程，认识数学在科学技术、社会发展中的作用，引导学生认识和感悟文化价值，树立文化自信、提升人文素养以及数学核心素养.为了更好的展现数学的科学价值和人文价值，数学文化类试题将作为一类重要的题型出现在考生面前.高中数学教师在平常教学中应该重视数学文化的渗透教育，同时，高中生对数学文化类试题要有足够认识，才能掌握正确的应对策略.为此，有必要对渗透数学文化的高考试题进行研究、整理.

一、数学文化类试题的基本认识

数学文化是指数学的思想、精神、方法、观点，以及它们的形成和发展；广泛地说，除了上述内涵外，还包含数学家、数学史、数学美、数学教育，数学发展中的人文成分，数学与社会的联系和数学与各种文化的关系，等等.基于上述数学文化的内涵，我们认为数学文化类试题即指包含数学的思想、精神、方法、观点的数学史料或有关数学知识的发生发展过程的数学试题，简称为文化类试题.根据数学文化类试题的描述，可以知道它与其他数学试题有所不同，具有如下特点：

（1）人文性：试题中包含一些数学史事件、数学名著、数学猜想或数学家的故事等富有文化韵味的史料，增强试题的文化内涵，在一定程度上传播了数学文化.

（2）趣味性：试题中蕴含的丰富的文化背景，可以提高学生的好奇心，在一定程度上激发学生学习数学知识和研究数学文化的兴趣.

（3）思想性：试题中包含的数学史料和融入部分数学知识的发展过程，充分展示了解决问题的思想方法，启发学生思维，较好的传播数学的思想和方法.

（4）创新性：试题中利用古代实际问题和著名算法与高中数学知识内容相互结合，实现旧法新用，增强数学文化的应用性，为问题的呈现、问题的解决提供新的视角.

（5）综合性：试题中利用充满文化韵味的背景材料将数学知识、方法和思想相融合，帮助学生了解多方面的数学内容，促进学生阅读理解、创新思维、问题探究、推广应用等综合能力的发展，实现更有效的教与学.

二、高考数学中的数学文化类试题的类型

1.“点缀式”试题

在某些试题的前面有一些具有明显数学史料特征的阅读材料，比如：数学家，数学名著和数学事件等背景，起到为试题本身创设独特的情景的作用.我们把这类数学文化类试题归类于点缀式.

例1 （2015年高考湖北理科第19题第1问）在《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑.如图1，在阳马PABCD中，侧棱PD⊥底面ABCD，且PD=CD.过棱PC的中点E作EF⊥PB交PB于点F，连接DE，DF，BD，BE.证明：PB⊥平面DEF.试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角；若不是，说明理由.

解析：因为PD⊥底面ABCD，所以PD⊥BC.因为底面ABCD为长方形，有BC⊥CD，而PD与CD相交于点D，所以BC⊥面PCD.而DE⊂面PCD，所以BC⊥DE.因为PD=CD，点E是PC的中点，所以在等腰直角三角形PDC中有DE⊥PC.而PC与BC相交于点C，所以DE⊥面PBC.因为PB⊂面PBC，所以PB⊥DE.又因为PB⊥EF，DE与EF相交于点E，所以PB⊥面DEF.由DE⊥面PBC，PB⊥面DEF可知，四面体DBEF的四个面都是直角三角形，即四面体DBEF是一个鳖臑，其四个面的直角分别为∠DEB，∠DEF，∠EFB，∠DFB.

本题采用一般几何方法求解，此外，还可以建立直角坐标系，以向量为工具用解析法证明（略）.

图1 阳马

评注：在例1中提到的阳马和鳖臑取自于 《九章算术》商功卷.命题者将《九章算术》与立体几何结合，利用阳马和鳖臑两锥体的定义，考查线线垂直与线面垂直的转化.对于这道试题我们可以抛去一些修饰成分的内容，抓住两锥体的定义的本质，即判断四面体BDEF的四个面是否是直角三角形.所以在解决“点缀式”试题的时候，我们可以借鉴处理新定义题的经验，对于审题和解答没有任何影响的“新名词”可以不用深究，抓住问题本质，学会对信息进行学习和迁移.

2.“复制式”试题

在高考题中，有一些为直接选取数学名题和数学名著中关于数学经典的问题、解法、证法等的原文，比如：《九章算术》便成为高考题中的常选项.我们将这类数学文化试题称为复制式试题.

例2（2013年高考湖北文科卷第16题）我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸.若盆中积水深九寸，则平地降雨量是______寸.（注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸）

解析：天池盆的几何形状是一圆台，该圆台过轴线的截面如图2所示.

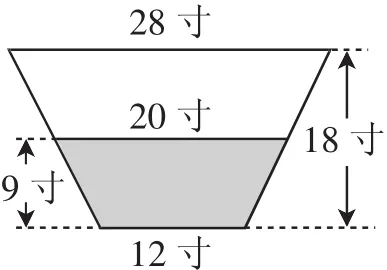
图2 圆台过轴线的截面

由图2可知，水深九寸，正好是盆深的一半，即盆中水面直径正好是上图梯形的中位线，因此，故盆中水面直径为20寸.设该圆台体积为：V=πh（R2+r2+Rr），其中R表示下底半径，r表示上底半径，h表示梯形的高，计算得V=588π，故平地降雨量为

评注：本题以中国数学史料为素材，对于题中数据进行说明，让试题回到考查学生的转化思想和对圆台体积公式的掌握上，在一定程度上凸显数学的实际应用价值.通过对《数书九章》中的“天池盆测雨”描述的理解提炼出图形，让试题的解答侧重在对圆台体积的计算方面.

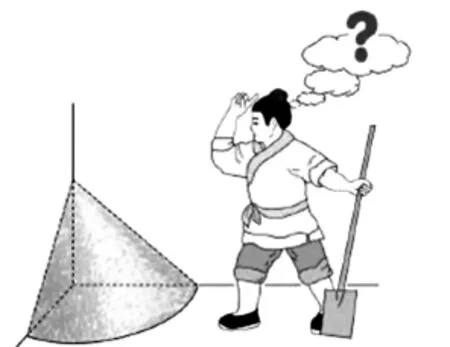
图3 米堆

例3（2015年高考全国卷1第6题）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图3所示，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（ ）.

（A）14斛 （B）22斛 （C）36斛 （D）66斛

故选B.

评注：该题采用《九章算术》第五章“商功”中关于生活生产中谷物储存的问题为背景，通过对文献原文进行简单的翻译，保留一些旧制度量单位，降低学生对题目理解的难度.这样的设计不仅考查学生对圆锥体积公式的掌握和单位的转换，而且让学生体会到数学要关注生产、生活等社会问题.这些都体现了数学的文化内涵.

例4（2011年高考湖北理科卷第13题）《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积______升.

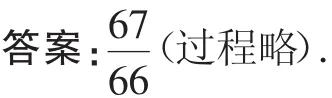
评注：本题借用《九章算术》中的“竹九节"问题，考查了学生对等差数列的通项公式和数列前n项和公式的掌握程度.因此，我们在解题时可抛去题目中的背景，抓住具体的数列，灵活运用公式，解决问题.

通过上述三个例题的分析，发现“复制式”类试题的题目中会有一些古文或者是一些不常见的度量词，但通过命题者对试题的处理，这些并不会影响学生对题意的把握.因此在解答这类试题时可以先看清楚问题，将问题作为突破口抓住解题线索，解决问题.

3.“内隐式”试题

在数学文化类试题中隐含着某个数学名题、数学猜想、数学结论、数学事件等内容，这只能在解题过程中不断的挖掘出来.因此我们把这类数学文化试题称为内隐式试题.

例5 （2015年高考湖北理科卷第14题）如图4所示，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2.

（Ⅰ）圆C的标准方程为______.

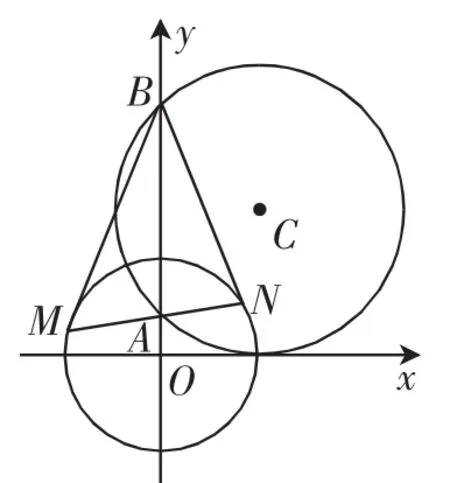
图4

（Ⅱ）过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，下列三个结论：①

其中正确结论的序号是______（写出所有正确结论的序号）.

解析：（Ⅰ）圆C的标准方程为：（x-1）2+（y-）2=2.

（Ⅱ）正确结论的序号是①②③.

评注：本题在考查命题的真假判断与应用和圆与圆的位置关系及其判定等知识的同时，隐含着著名的阿波罗尼斯圆：平面内到两个定点的距离之比为常数（大于零且不为1）的点的轨迹为圆.让学生在解题中感受阿波罗尼斯圆的魅力.

通过对上述例题的分析，体会“内隐式”类试题中所包含的数学文化并非直接展示在题面上，往往隐藏在题意中，不会额外增加试题的难度，只是让学生在一步一步分析题意中，领略数学文化的魅力，传播数学文化.

4.“改编式”试题

在数学文化类试题中，利用一些有趣的数学史料、数学名题等与高考所涉及的相关数学知识相互融合，进行合理的改编.将数学经典的问题添加上当代数学的记号，为试题创设适当的情景，使其更好地达到考查目的.我们把这类数学文化试题归类于改编式试题.

例6（2016年高考四川文科卷第8题）秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图5所示的程序框图给出了利用秦九韶算法求多项式值的一个实例，若输入n，x的值分别为3，2，则输出v的值为（ ）.

（A）35 （B）20

（C）18 （D）9

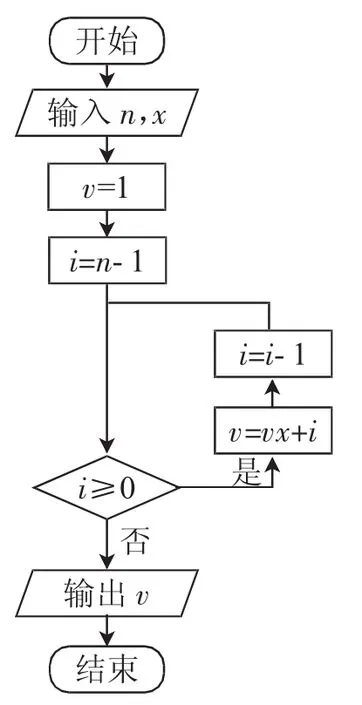
图5 秦久韶算法框图

解析：通过将初始值n=3，x=2的代入程序框图中，判断“i≥0”是否成立来运行程序，最后当i=-1输出结果v=18.故选C.

评注：本题将著名的秦久韶算法融入程序框图中，在传播秦久韶算法的同时，考查学生对程序框图的把握，彰显了《数书九章》中提出的多项式求值算法的先进性.而且在2016年的全国卷2文理科和四川理科卷也将著名秦九韶算法融入到程序框图中考查，可以看出大家对这种考查方式的喜爱.

例7 （2009年高考湖北理科卷第15题）已知数列{an}满足：a1=m（m为正整数），

若a6=1，则m所有可能的取值为______.

解析：m所有可能的取值有：32，5，4.

评注：该题以“角谷猜想”与数列推导公式相融合考查学生的推导能力，同时让学生感受到“角谷猜想”中无论初始值有多大的误差，最后都能自行恢复的奇妙，体现数学的美妙之处.

例8 （2011年高考湖北理科卷第15题）n个自上而下相连的正方形着黑色或白色.当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如图6所示：

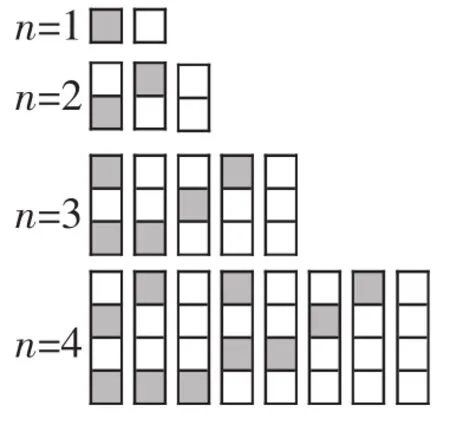
图6 黑色正方形互不相邻的着色方案

由此推断，当n=6时，黑色正方形互不相邻的着色方案共有______种，至少有两个黑色正方形相邻的着色方案共有______种.（结果用数值表示）

解析：设n个黑色正方形互不相邻的着色方案数为an，由图6可知a1=2，a2=3，a3=5，a4=8.则有a3=a1+a2，a4=a2+a3.由此推断a5=a3+a4=5+8=13，a6=a4+a5=8+13=21.故黑色正方形互不相邻的着色方案共有21种；因为每个正方形着黑色或白色有2种方法，所以6个正方形一共有26=64种方法，至少有两个黑色正方形相邻的着色方案共有64-21=43（种）着色方案，故分别填21，43.

评注：本题在斐波那契数列的基础上，以图形为依托与排列组合相融合，学生通过对图形的把握，总结规律解决问题.这种设计既考查排列组合知识，又考查学生的归纳猜想能力和合情推理意识.

通过对上述例题的分析，从命题的角度看，这些试题是基于数学文化，将经典数学问题或解法与高考数学考点相结合改编，使试题在考查数学知识的同时被添加了一层历史的色彩.因此在解决这类试题时要学会分析整合试题中出现的数学文化知识，做到知识的迁移运用，透过表面现象去洞察问题的实质.

5.“复合式”试题

数学文化类试题的类型除了以上“点缀式”“复制式”“内隐式”“改编式”外，还有“附加式”“顺应式”等方式，这些方式在表现形式上是较为单一的.事实上，当数学文化不再是以单一的方式而是通过多种方式融入到试题中时，我们可以将这类数学文化类试题归类于“复合式”.

例9（2009年高考湖北理科卷第10题）古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如他们研究过图7中的1，3，6，10，…由于这些数能够表示成三角形，将其称为三角形数；类似的，称图8中的1，4，9，16，…这样的数为正方形数.下列数中既是三角形数又是正方形数的是（ ）.

（A）289 （B）1024 （C）1225 （D）1378

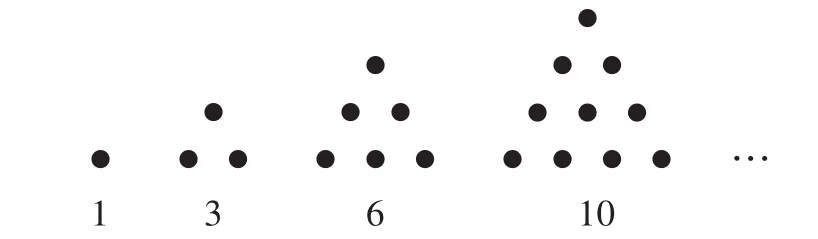
图7 三角形数图

图8 正方形数图

评注：本题以古希腊毕达哥拉斯学派研究的多边形数为试题的文化背景，通过与数列的结合进行改编，考查了学生对多边形数的了解和归纳推理的能力，而且题目中也暗含了古希腊的阿基米德的群牛问题.此外，由本题的三角形数还可以延伸到对四角形数、五角形数和六角形数等的研究.因此本题在多方面的考查学生的知识和能力的同时还蕴藏着深厚的数学文化.

三、基于“数学文化类”试题的教学要求和应对策略

1.教师教学要求

作为数学教师我们要努力提升自身的数学文化素养，重视数学文化类试题的研究.因此，教师要多学习数学文化的研究论著和数学经典名著，挖掘其中可以运用到课堂教学中的相关数学文化知识，数学文化精神等，能够体会到数学的美，明白数学并不只是计算的工具，它除了理性精神、科学精神外，还含有丰富的人文精神.教师要了解材料背后的教学价值，全面提升自己的文化素养，这样才能更好地引导学生挖掘试题中的数学文化，有效地解决数学文化类试题，传播数学文化.

将数学文化类试题融入教学，不仅可以消除学生对该类试题的陌生感，而且可以帮助学生更好地了解数学文化，同时领略数学方法、思想和精神的魅力.此外，为了使数学文化更深入课堂，教师也可以有意开发教材资源，探究历史名题，创设经典游戏情境，开拓学生视野，加深对数学学科历史和本质的认识，从而实现数学文化浸润.或者在讲解定义、定理和公式时可以借助数学文化帮助学生理解，提高学生的学习兴趣，突破教学难点.也可以结合学生的实际情况，选取难度适中的内容围绕数学文化展开微型探究.比如，教师可以选取一些数学名题引导学生发现数学所呈现出来的美，使学生在逻辑算术的熏陶中获得一种深层的理性文化素养.

2.考生应对策略

通过对高考中的数学文化类试题的分析，可以发现文化类试题在高考中越来越被重视，而且不同分类下的数学文化类试题的处理方法有所不同.对于“点缀式”试题，我们可以将对解答没有任何影响的“新名词”舍去，不用刻意纠结题中出现的数学文化背景，抓住本质解决问题；对于“复制式”试题，我们可以先看问题，将问题作为突破口来理解题意，这样会更容易抓住线索解决问题；对于“内隐式”试题，我们可以在解题中体会其中暗含的文化底蕴，明确解题思路，有效地解决问题；对于“改编式”试题，我们要了解其中的文化背景，学会知识的迁移运用，冷静地透过表面现象去洞察问题的实质；对于“复合式”试题，我们要挖掘出题中暗含的文化背景，根据问题得出隐含的条件，从而帮助解决问题，这需要将数学文化与多方面能力进行结合.