一种自适应低剂量CT图像质量改善算法

蒋慧琴，徐玉风，马 岭，杨晓鹏，Toshiya Nakaguchi

(1.郑州大学 信息工程学院，河南 郑州 450001； 2.郑州大学第一附属医院 医学装备部，河南 郑州 450052； 3.日本千叶大学 先端医工学研究中心, Chiba)

0 引言

为了解决CT检查导致的辐射剂量过高问题，低剂量CT扫描逐渐成为临床应用热点.然而，低剂量CT扫描会导致图像质量退化，特别是LDCT图像中的噪声会严重影响诊断精度.因此，去除噪声是改善低剂量CT图像质量的重要任务.低剂量CT扫描所引起的噪声主要是X射线量子噪声[1].针对图像中的细节和噪声同属高频成分难以分离的经典难题，小波变换等多尺度分析方法呈现出一定的优势[2].近几年，许多学者已提出大量的小波域去除量子噪声方法[3-4].主要包括两种思路：其一，假设其服从Gaussian分布，利用阈值法去噪，如小波硬阈值、软阈值和贝叶斯阈值法等[3].其二，假设其近似服从Poisson分布.首先利用方差稳定变换将其转化为近似服从Gaussian分布的噪声，再利用去除Gaussian噪声的常用方法进行处理[4-7].随着多尺度分析方法的发展，一些学者提出了基于剪切波变换的图像去噪算法.例如，Dan等[8]提出的基于剪切波变换的贝叶斯最大后验估计方法，能有效去除因小波去噪产生的伪吉布斯效应；胡海智等[9]提出的全变差正则化剪切波域收缩方法，能更有效地去除Gaussian噪声并保留图像中的细节信息等等.为了去除低剂量CT图像中的量子噪声，笔者假设量子噪声近似服从Poisson分布，并利用Anscombe变换，将原图像中的噪声转化为一个具有近似常数方差的Gaussian噪声.然而，由于传统Anscombe变换对低信噪比的图像其噪声方差无法趋于稳定[10]，致使去噪效果欠佳.为了解决这一问题，文献[11]通过最优化Anscombe逆变换以改进去噪效果；Zhang等[12]通过改进Anscombe变换，使当Poisson噪声参数λ>0.1时，其噪声方差可以趋于稳定.但是，当λ≤0.1时，该方法仍不能使噪声方差稳定到一个常数值.基于前期研究[7]可知，当Poisson噪声参数λ≤0.1时，如在应用Anscombe变换的基础上，再利用阈值法去除量子噪声可以取得更好的效果，但其去噪效果依赖于噪声方差值的估计精度.

鉴于此，笔者针对低信噪比的剪切波高频系数子带，提出基于剩余自相关功率的噪声方差估计方法，并结合贝叶斯最大后验估计提取出非噪声高频系数，从而有效地提高低信噪比图像的去噪效果.

1 剪切波变换

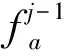
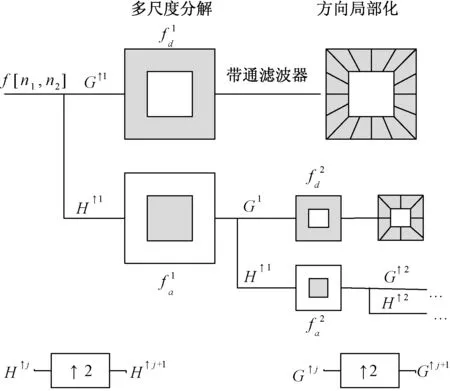
图1 剪切波分解算法框架Fig.1 The block diagram of shearlet decomposition

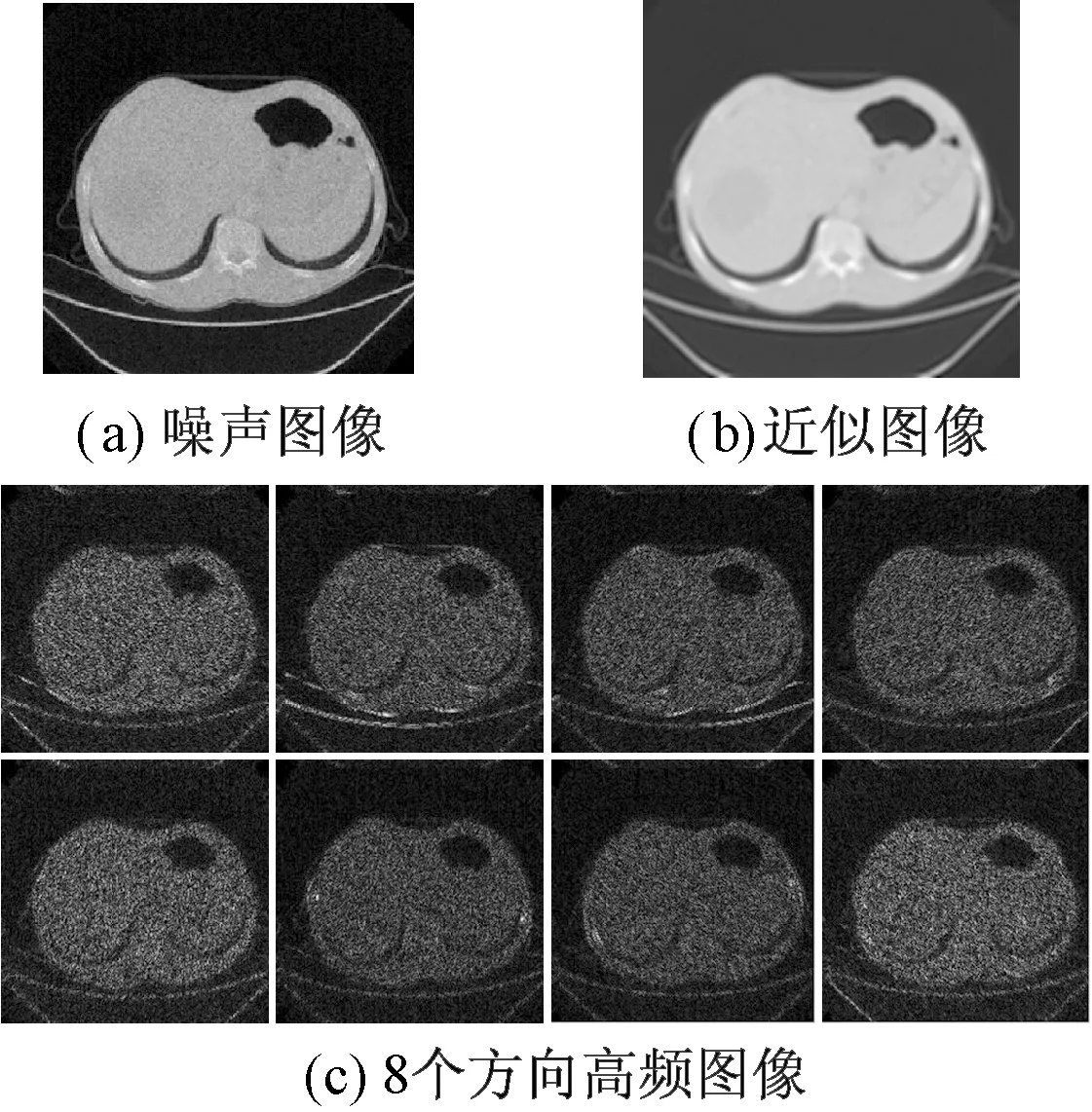
图2 剪切波分解的一层图像Fig.2 The shearlet coefficients at one scale

2 改进的噪声方差估计算法

虽然Donoho提出的噪声方差计算方法(MAD方法)被广泛应用,但因其是针对小波域估计高斯噪声方差而设计，存在一定误差.为此，剩余自相关功率(RAP)[10]与贝叶斯最大后验估计相结合的改进噪声方差估计精度的方法，其实现过程如下.

2.1 贝叶斯最大后验估计

设

g=f+w，

(1)

式中：f和g分别表示原图像和加噪后的图像；w表示均值为0的Gaussian白噪声.

设

y=x+n，

(2)

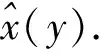
基于贝叶斯最大后验估计计算该近似值的步骤如下.

(1)用Donoho提出的估计方法计算噪声方差近似值:

(3)

其中，yi,j表示选取的高频子带系数.

(2)计算提取非噪声剪切波高频子带系数的阈值如下：

(4)

(5)

(6)

(3)用贝叶斯最大后验估计法提取高频子带中非噪声剪切波系数近似值：

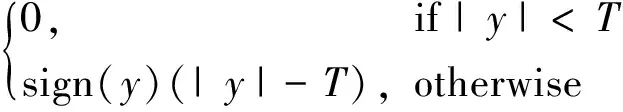
(7)

2.2 噪声方差估计

对CT图像加入均值为0的Gaussian白噪声，用非下采样剪切波对图像进行尺度为4的分解，每层选定一个方向.由于随着分解层数的增加，高频子带的图像信息逐渐减少，而噪声信息逐渐增多，且第4层高频子带的信噪比最低，故笔者分别用MAD方法和剩余自相关功率方法计算含噪图像第4层高频细节子带的噪声方差，并对实验结果进行比较，其实现步骤如下.

(1)选取噪声方差的候选值.利用式(3)计算所选高频子带的噪声方差σm，并且以该值为中心,间隔为0.1, 选取30个噪声方差候选值∑=[σ1,σ2,…,σm,…,σ30].

(2)计算所选高频子带所需的阈值.针对选定的每一个噪声方差候选值σm，利用式(4)所示的贝叶斯最大后验估计方法计算阈值[8].

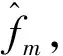
(8)

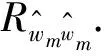
(9)

其中,N是自相关中点的数量.当真正的噪声方差为20时，基于不同的噪声方差候选值计算出其对应的Pm，其对应关系如图3所示.从图3可以看出，其对应的Pm在接近真正的噪声方差时有一个突变，且之后Pm趋于稳定.

(5)计算噪声方差.为了捕捉Pm的这种特性，记

Dm=Pm+1-Pm.

(10)

不同的噪声方差候选值与Dm的对应关系如图4所示，从图4可以看出，真正的噪声方差即当Dm达到最大值时对应的σm右侧一个较小的值，这个值的估计公式为:

mmax=argmmaxDm.

(11)

(12)

σ(RAP)=σm*.

(13)

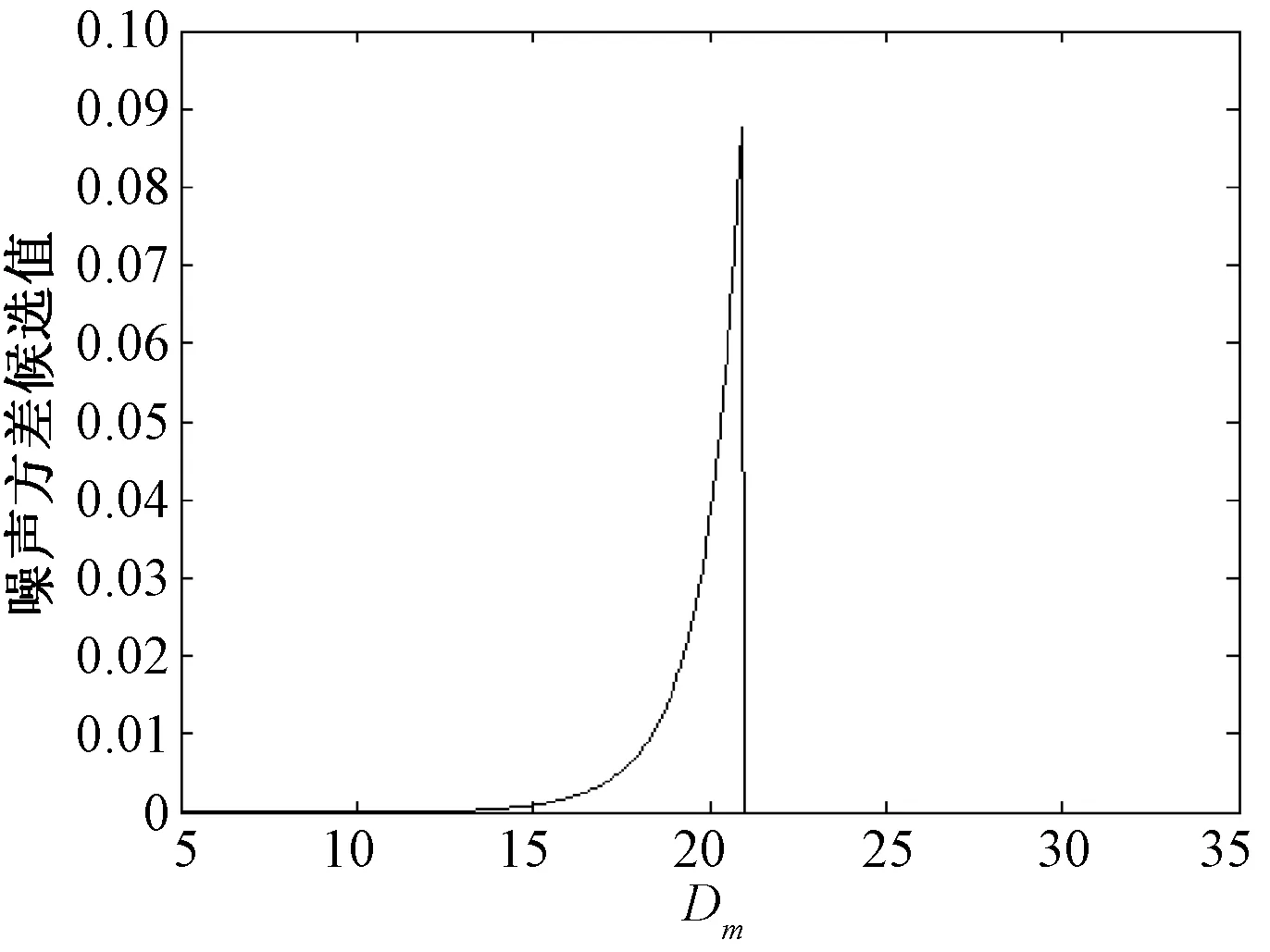
图3 当噪声方差为20时的剩余自相关功率Fig.3 Residuals autocorrelation power (RAP) when the true variance is 20

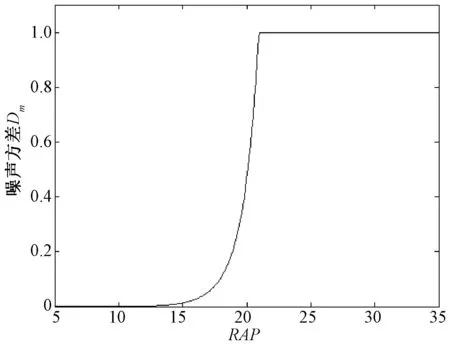
图4 对应图3不同的RAP由式(10)所得的DmFig.4 Difference of RAP, Dm in(10),for the RAPs in Fig.3

为了验证该方法的准确性，对常规剂量的CT图像加入均值为0、方差不同的Gaussian白噪声进行一系列的仿真实验，实验结果如表1所示，表示同一幅CT图像加入的Gaussian白噪声方差分别为5、10、15、20、25时的实验结果.

表1 同一图像Gaussian白噪声方差不同时实验结果对比Tab.1 Comparison of results in the same image with different White Gaussian noise variances

由表1的实验结果可以看出，对不同的Gaussian白噪声方差，本文算法的估计精度均高于文献[3]中的MAD方法.

3 本文算法

笔者提出的自适应低剂量CT图像质量改善算法，其算法框图如图5所示，主要包括5个步骤.

图5 本文算法框图
Fig.5 The diagram of the proposed algorithm

步骤1：Anscombe变换.首先采用Anscombe变换将低剂量CT图像中的量子噪声转变为具有近似常数方差Gaussian噪声[10].变换公式为：

(14)

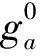
步骤2：剪切波分解.将Anscombe变换后的图像进行4层剪切波分解，每层分解为8个方向，得到1个低频图像和32个高频图像.

步骤3：提取非噪声系数.由于随着分解层数的增加，高频子带的信噪比逐渐降低，故利用提出的噪声方差估计方法对信噪比较低的第3、4层高频子带估计其噪声方差.然后基于噪声方差估值，结合贝叶斯最大后验估计方法提取非噪声高频系数.

步骤4：重构图像.基于步骤3获得的非噪声高频系数和低频系数进行剪切波逆变换，获得去噪图像；对去噪后的图像实行Anscombe逆变换，得到重构图像.公式为：

(15)

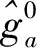
4 仿真实验

笔者从定量评价和视觉效果来验证提出算法的有效性.采用PSNR(peak signal to noise ratio)值和MSSIM(mean structure similarity)值[11]为定量评价指标:

(16)

(17)

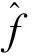
4.1 定量评价

对取自郑州大学第一附属医院的一系列含有病变的、大小为512×512的常规剂量的胸部CT图像加入参数λ≤0.1的Poisson噪声，并进行仿真实验，采用PSNR和MSSIM来定量评价去噪效果,实验结果如表2和图6所示.

表2表示对10幅常规剂量的CT图像添加强度参数λ=0.01的Poisson噪声，利用本文方法与文献[3]方法对噪声图像进行去噪的实验结果.

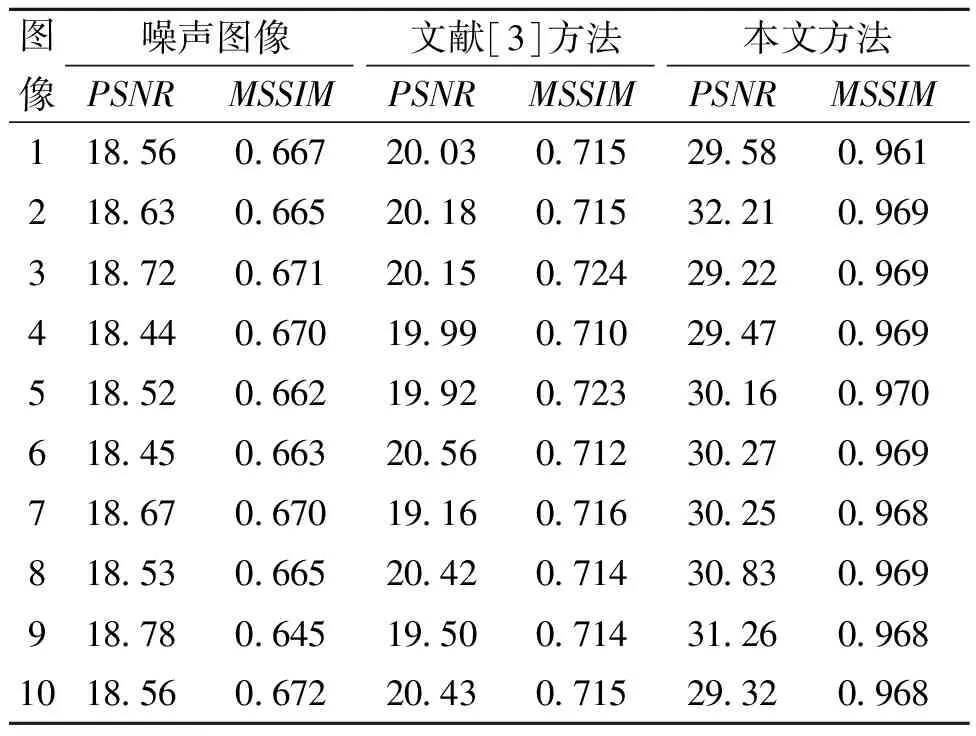
表2 当Poisson强度λ=0.01时的PSNR和MSSIM比较Tab.2 Comparison of PSNR and MSSIM when the Poisson noise intensity is 0.01 dB

图6表示对一幅CT图像添加强度参数λ为0.005、0.008、0.010、0.050、0.080和0.100的Poisson噪声，本文方法与文献[7]方法对噪声图像去噪的实验结果.图6(a)表示随着噪声量的变化，两种算法的重构图像与噪声图像的PSNR折线图，图6(b)表示随着噪声图像的MSSIM变化，两种算法的重构图像的MSSIM折线图.

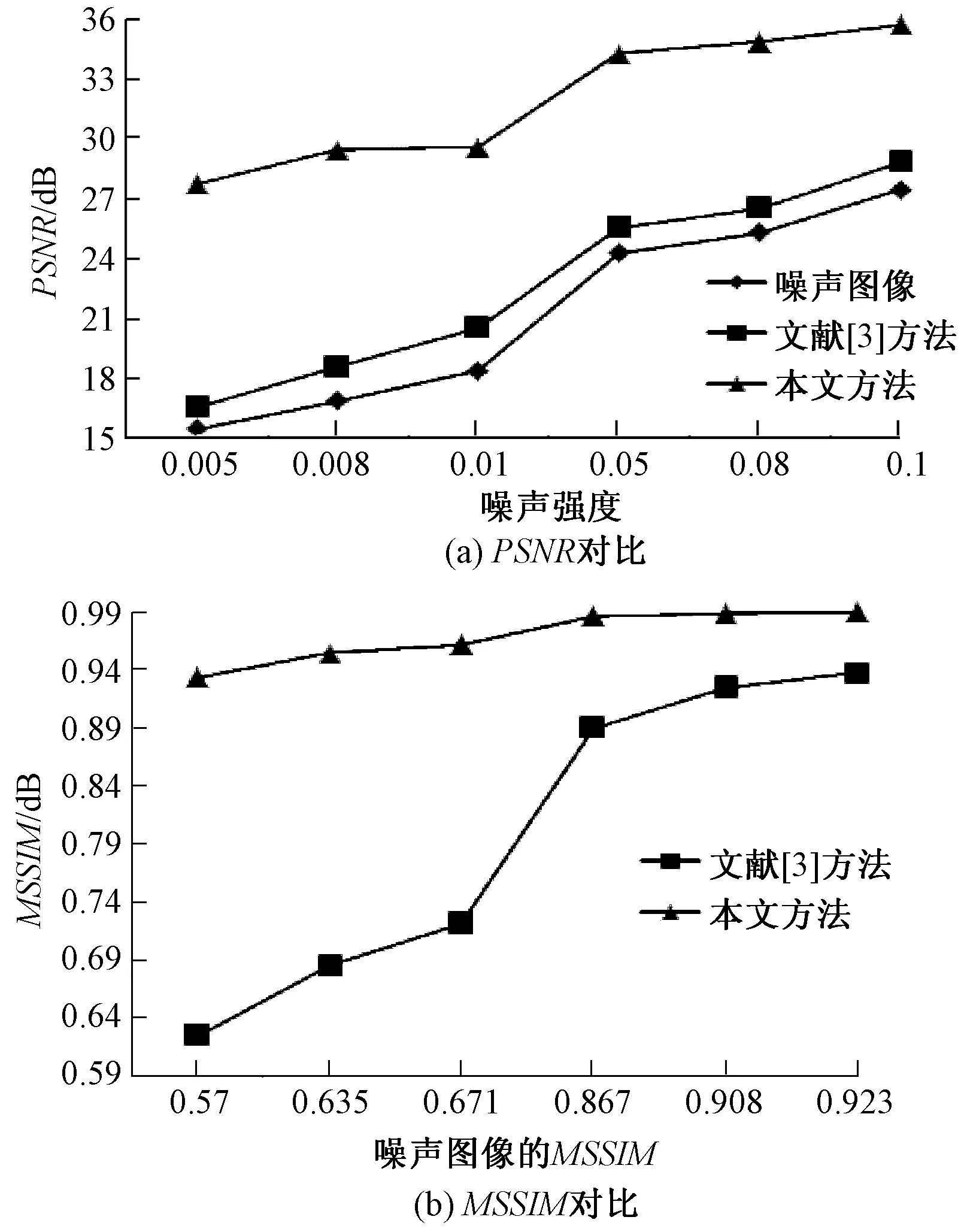
图6 不同Poisson噪声强度时的PSNR和MSSIM对比图Fig.6 Comparison of PSNR and MSSIM in image with different Poisson noise intensity

由表2可知，本文方法与文献[3]方法相比，PSNR和MSSIM分别提高了52.2%和34.9%.从图6可以看出，对参数λ≤0.1的Poisson噪声，本文算法所得重构图像的PSNR和MSSIM均高于文献[3]方法；本文方法在噪声量较多的情况下，去噪效果尤为突出.

表2和图6的实验结果表明，对参数λ≤0.1的Poisson噪声，无论是同一噪声强度下的不同图像还是多种噪声强度下的同幅图像，与文献[3]方法相比，本文算法所得重构图像的PSNR和MSSIM均有所提高.由此得出，本文算法具有较强的自适应性和鲁棒性.

4.2 视觉效果

本文视觉效果评价采用在日本千叶大学先端医、工学研究中心，以体膜为扫描对象，进行低剂量扫描所采集的降低不同剂量的多幅实际CT图像.低剂量扫描的主要原理是利用放射线剂量与管电流的线性关系，当保持其他参数不变时，通过降低管电流和管电压来降低放射剂量.图7(ai)(i=1,2)所表示图像的扫描参数设置分别为管电压120 kV，扫描层厚为0.5 mm，管电流分别为100 mA和150 mA；图7(a3)表示图像的取像参数设置分别为管电压为120 kV，管电流为200 mA，扫描层厚为1 mm.

从图7(ai)(i=1,2,3)可知，随着管电流的减少，噪声量越来越多.分别用本文方法与文献法对这些图像进行仿真实验，实验结果分别由图7(bi)和图7(ci)(i=1,2,3)表示.图7(bi)(i=1,2,3)为利用文献[3]方法所获得的去噪图像，图7 (ci)(i=1, 2,3)分别表示本文方法的重构图像.由图7可以看出，本文算法不仅能有效去除噪声，而且与文献[3]方法相比能更好地保留图像中的边缘信息和纹理信息.

上述实验的定量分析和视觉效果表明，本文算法具有自适应地去除参数λ≤0.1的Poisson噪声的能力，而且该方法有效提升了重构图像的质量.

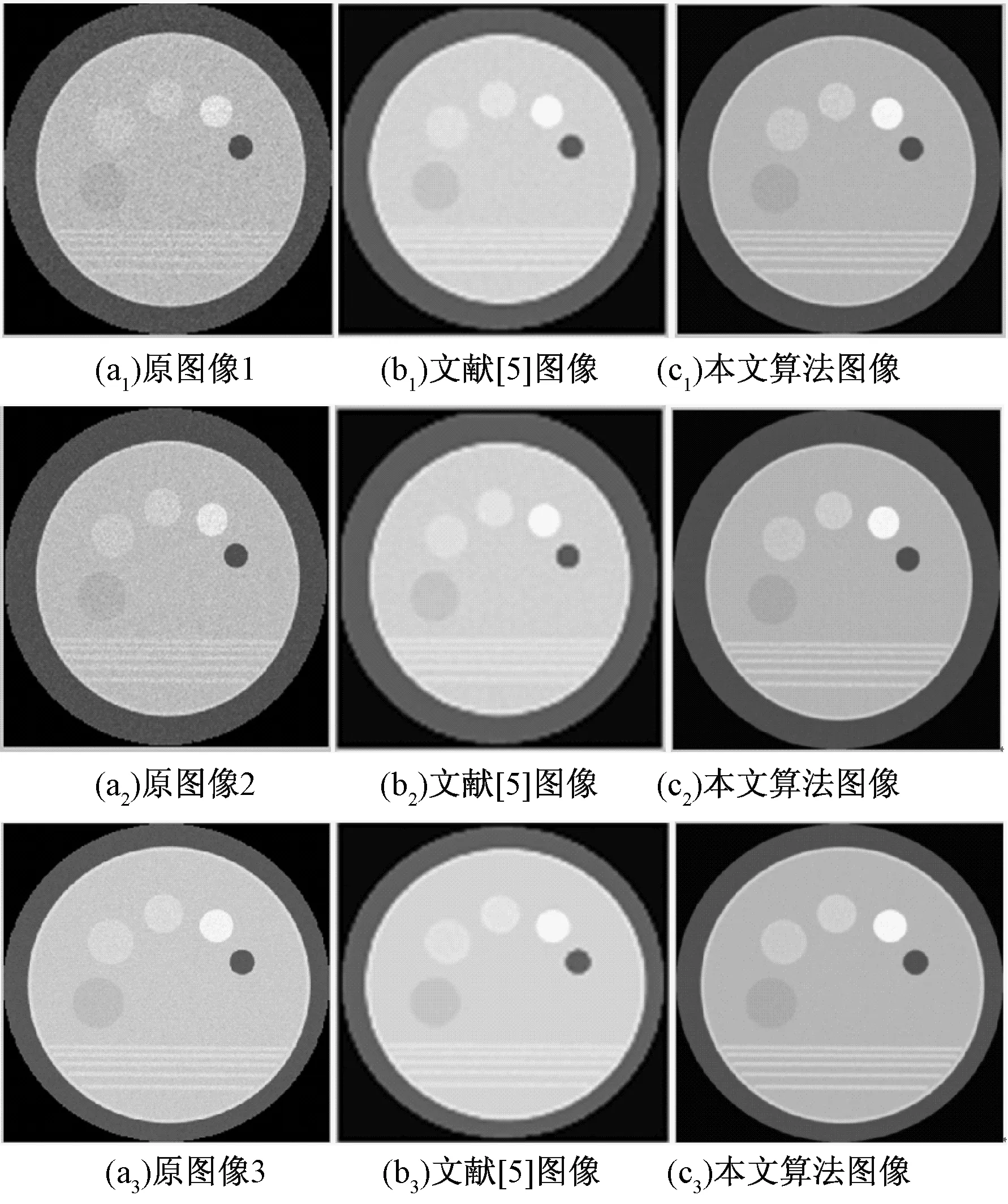
图7 低剂量CT图像去噪效果对比Fig.7 The comparison of de-noising effects for low-dose CT

5 结论

笔者利用剪切波良好的稀疏特性，将Anscombe变换与改进的自适应噪声方差估计算法相结合，提出了一种有效改善低剂量CT图像质量的方法.对含有λ≤0.1的Poisson噪声的CT图像进行的定量评价.结果表明，本文方法与文献[3]方法相比，其PSNR平均提高52.2%，MSSIM提高34.9%.同时，利用本文方法和文献[3]方法对多幅实际低剂量CT图像进行去噪的对比实验结果也表明，本文方法较文献[3]方法可以更好地保留图像细节信息.因此，本文算法具有自适应能力强、重构图像质量高的特点，具有一定的临床应用价值.