A GENERALIZATION OF GAUSS-KUZMIN-LÉVY THEOREM∗

Peng SUN(孙鹏)

China Economics and Management Academy,Central University of Finance and Economics,Beijing 100081,China

E-mail:sunpeng@cufe.edu.cn

Abstract We prove a generalized Gauss-Kuzmin-Lévy theorem for the generalized Gauss transformation

Key words Gauss transformation;transfer operator;Gauss’problem;Hurwitz zeta function

1 Introduction

Let p be a positive integer.We consider the following generalized Gauss transformation on[0,1]:

where{x}is the fractional part of x.Such transformations were first introduced in[3](the associated continued fractions had appeared in[2])and also studied in[7,8,11].For every p,Tphas a unique absolutely continuous ergodic invariant measure,

where m is the Lebesuge measure on[0,1].Equivalently,

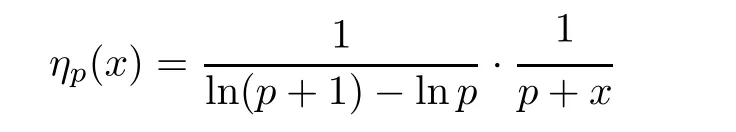
is the unique continuous eigenfunction of the transfer operator corresponding to the eigenvalue 1.We remark that G1is the so-called Gauss-Kuzmin-Wirsing operator introduced in[5].Detailed discussion on this operator can be found in[4].

Denote

Let

Gauss has shown that

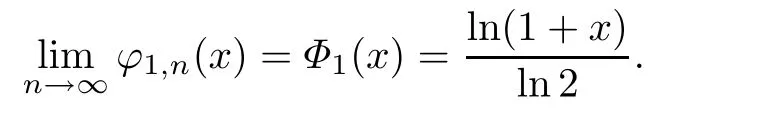
In 1812,he proposed the problem to estimate

The first solution was given by Kuzmin[6],who showed in 1928 that

as n → ∞ for some q∈ (0,1).In 1929,Lévy[9]established

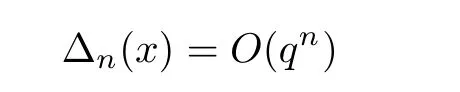
In this article,we would like to follow an approach in[10]to generalize Lévy’s result for all

Theorem 1.1For every positive integer p and every x∈[0,1],

where

and

are the Hurwitz zeta functions.

Remark 1.2We would like to thank an anonymous referee from whom we learned that there is a similar result in[7,Theorem 1.1(ii)].Compared to it,we have a different approach and the main novelty of Theorem 1.1 is the explicit expression of Qp,which is an upper bound of the exponential rate of decay for

As a generalization of Lévy’s result[9]onit is natural to expect thatalso decays exponentially.Our motivation is to see how the rate depends on p.The estimate we have for Qpshows that Qp→0 as p→ ∞.Furthermore,it provides the first order termSo,generally it is faster that ϕp,nconverges to Φpas p grows.This is the most interesting fact we observe in this work.

2 Proof of the Theorem

For fixed p,we have

and

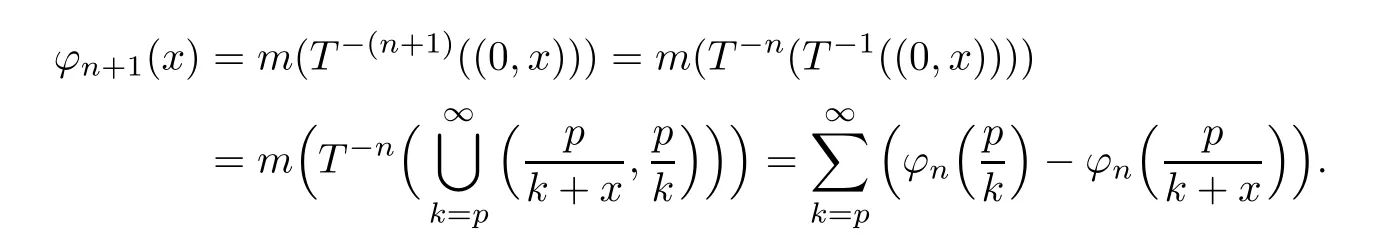
This recursive formula implies that ϕnis differentiable(actually analytic)and hence

So,it is enough to study the operator Gp.Note that(1.1)holds if

We can actually show a more general result:

Theorem 2.1Let f∈C1([0,1])such that

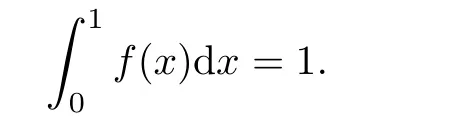
Then,for every positive integer p and every x∈[0,1],we have

ProofFix p.Let

Then,

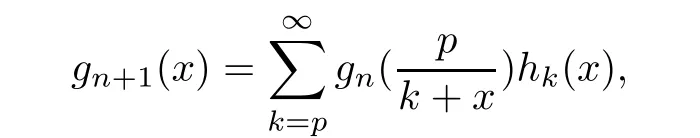
where

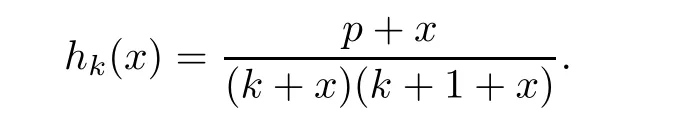
Note that

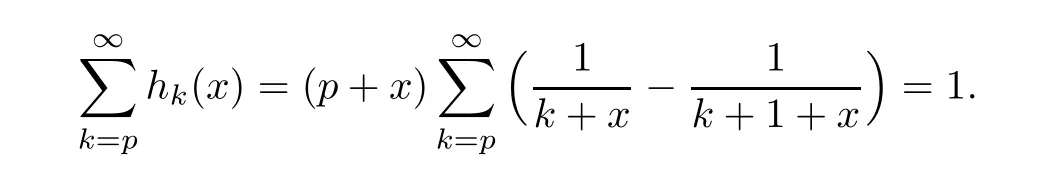
So

Moreover,for every k≥p and x∈[0,1],

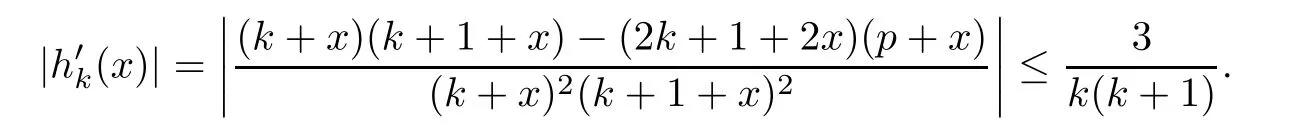
Note that gn∈C1[0,1].Let

be the norm of gnin C1[0,1].Then,for every k≥p and x∈[0,1],we obtain

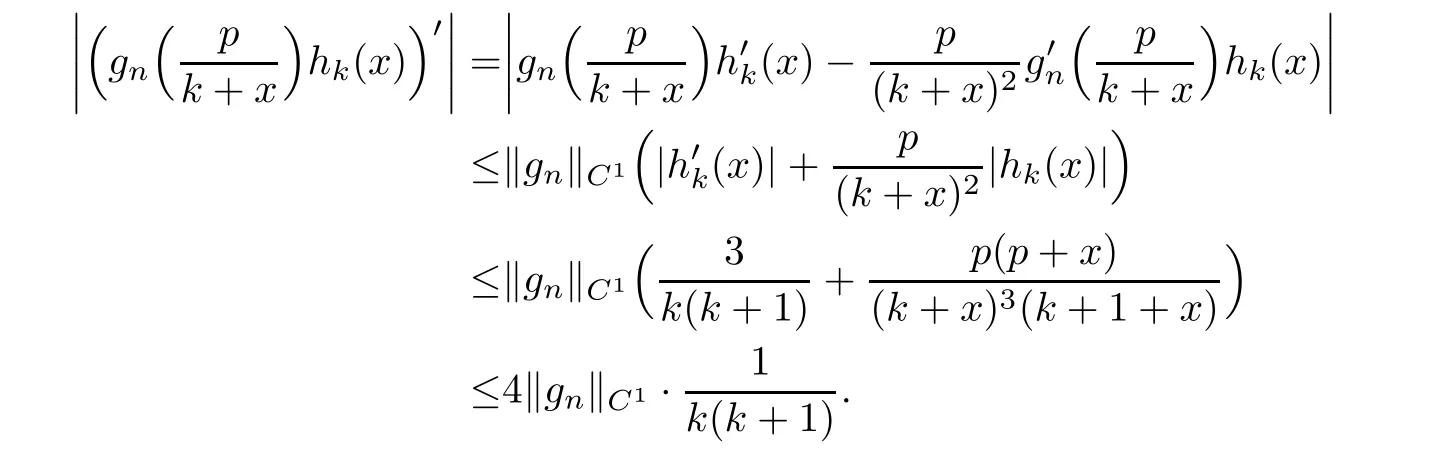
This implies that

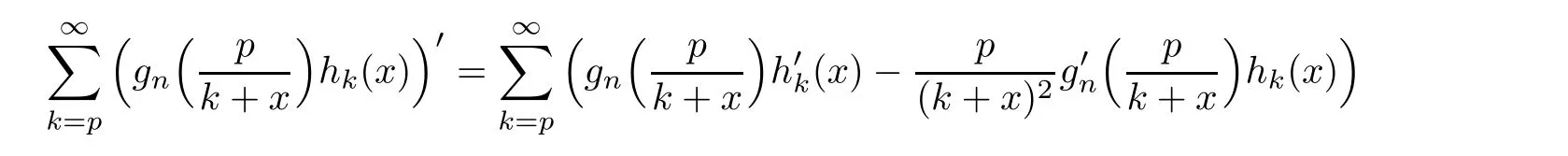
converges absolutely and the sequence of its partial sums converges uniformly.Hence,we have

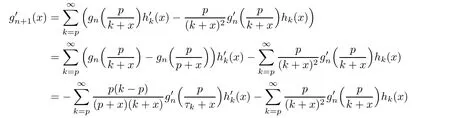
for some τk∈ [p,k],k=p,p+1,···.

Let k·k be the maximum norm on C[0,1],the space of all continuous functions on[0,1],andthat is,

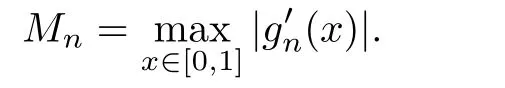
Then,

for

and

for every k≥p.

Let

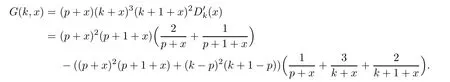
If p≤k≤2p,then

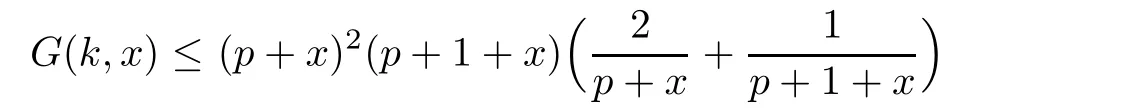
If k≥2p+1,then

But for k≥2p+1,

So,for k≥2p+1,

Therefore,for all integers k≥p and all x∈[0,1],we have G(k,x)<0.Equivalently,Hence,

We will show in Theorem 3.1 that,which implies that,there is a constant c∈R such that

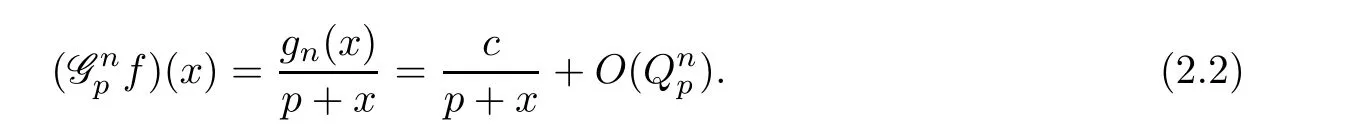
We note for any integrable function ψ,

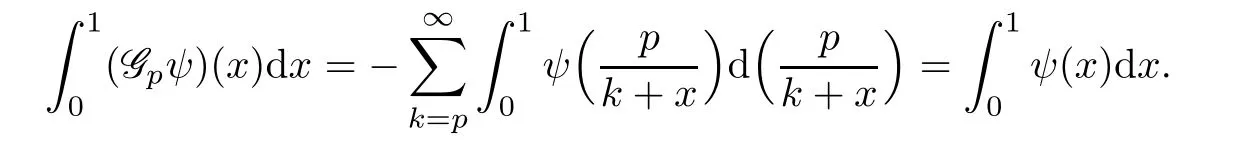
So,for all n,

Hence in(2.2)we must have

Remark 2.2A direct corollary of Theorem 2.1 is

However,the idea of the proof actually relies on the knowledge that ηp(x)is invariant of Gp:We presume that(2.3)holds.So,we make the substitution(2.1)and consider the derivative of

3 Estimate of the Constant

Now,we evaluate Qp.If p=1,then Q1=2ζ(3)− ζ(2)<0.76,where ζ(n)is the Riemann zeta function.For p≥2,the following estimate is not too bad.

Theorem 3.1For every positive integer p,

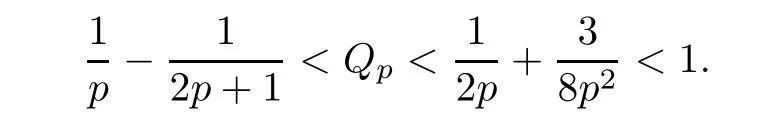
Remark 3.2This implies that

Applying results on asymptotic expansions of Hurwitz zeta functions or polygamma functions(cf.[1]),we actually have

ProofFix p.For

we have

and

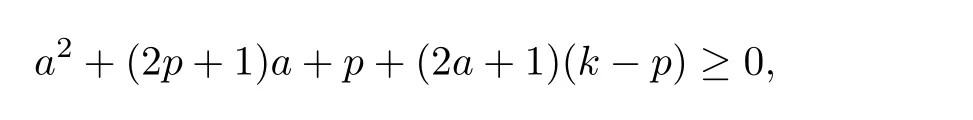
that is,

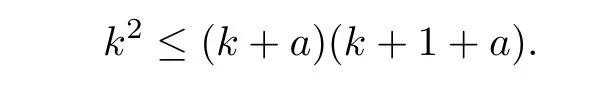
Hence,

For

we have

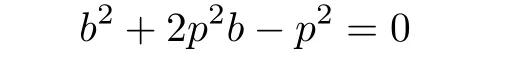
and

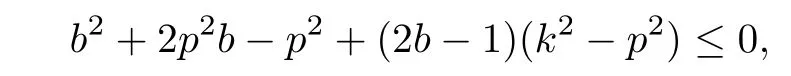
that is,

Hence,

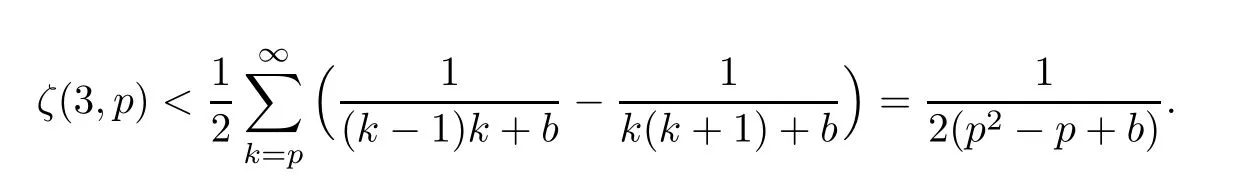
Therefore,

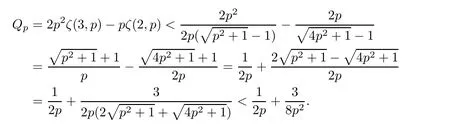
Meanwhile,

Hence,