NONNEGATIVITY OF SOLUTIONS OF NONLINEAR FRACTIONAL DIFFERENTIAL-ALGEBRAIC EQUATIONS∗
Xiaoli DING(丁小丽)
Department of Mathematics,Xi’an Polytechnic University,Shaanxi 710048,China E-mail:dingding0605@126.com
Yaolin JIANG(蒋耀林)
Department of Mathematics,Xi’an Jiaotong University,Shaanxi 710049,China
Abstract Nonlinear fractional differential-algebraic equations often arise in simulating integrated circuits with superconductors.How to obtain the nonnegative solutions of the equations is an important scientific problem.As far as we known,the nonnegativity of solutions of the nonlinear fractional differential-algebraic equations is still not studied.In this article,we investigate the nonnegativity of solutions of the equations.Firstly,we discuss the existence of nonnegative solutions of the equations,and then we show that the nonnegative solution can be approached by a monotone waveform relaxation sequence provided the initial iteration is chosen properly.The choice of initial iteration is critical and we give a method of finding it.Finally,we present an example to illustrate the efficiency of our method.
Key words Fractional differential-algebraic equations;nonnegativity of solutions;waveform relaxation;monotone convergence
1 Introduction
Fractional calculus has been used widely to deal with some problems in fluid and continuum mechanics[1,2],viscoelastic and viscoplastic flow[3],epidemiological models[4,5],and circuit simulation with superconductor materials[6].The main advantage of fractional derivatives lies in that they are more suitable for describing memory and hereditary properties of various materials and process in comparison with classical integer-order derivative.In these years,various theory and numerical solutions to fractional differential equations were extensively investigated.For example,collocation methods were applied into solving fractional differential equations([7,8]).Gong et al[9]gave an efficient parallel solution for Caputo fractional reaction-diffusion equation with explicit method.The parallel solution is implemented with MPI parallel programming model.Stokes et al[10]proposed a method to accelerate the computation of the numerical solution of fractional differential equations.Xu et al[11]applied parareal method into solving time-fractional differential equations.Mohammed Al-Refai and Yuri Luchko gave maximum principle for the multi-term time-fractional diffusion equations with the Riemann-Liouville fractional derivatives[12].
The investigation of positive solutions of different classes of fractional differential equations is a relevant question in real world prolems.For example,some authors in[13,14]discussed the existence of positive solutions of nonlinear fractional differential equations.Some authors[15,16]investigated positive solutions of fractional differential equations with integral boundary conditions and multi-point boundary conditions,respectively.Li[17]discussed the nonexistence of positive solution for a semi-linear equation involing the fractional Laplcian in RN∗.Wang et al[18]gave the existence of solutions for nonlinear fractional differential equations using monotone iterative method.In[19],Kaczorek discussed positive linear systems consisting of n subsystems with different orders,where the proposed system can be described by linear fractional differential-algebraic equations.However,as far as we known,nonnegativity of solutions of nonlinear fractional differential-algebraic equations is still not studied.
In this article,we consider nonnegativity of solutions of nonlinear fractional differential algebraic equations using waveform relaxation(WR)algorithm.It is well known that the WR method is a dynamic iterative method.It was originally proposed to simulate large circuits in[20]and it was widely studied.Until now,the method has been applied into solving ordinary differential equations[21],differential-algebraic equations[22],functional differential equations[23],and fractional differential equations[24].As usual,the waveform sequence computed by the algorithm is not monotone.In this article,we identify the nonlinear fractional differential algebraic equations which satisfy certain Lipschitz conditions,such that if the initial iteration waveform is chosen properly,the waveform sequence converges to the nonnegative solution monotonically.
This article is organized as follows.In Section 2,we present some notations,definitions,and assumptions.In Section 3,we firstly examine monotone dependency on initial conditions and inputs.Then,we state the main theorem on nonnegative solution.Finally,we give a method to choose the initial iteration.In Section 4,we present an example with numerical simulations to illustrate the waveform relaxation algorithm.
2 Preliminaries
In this section,we give some basic concepts and notations.
Definition 2.1([26]) Let[a,b]be a finite interval on the real axis R.The Riemann-Liouville integraland the Riemann-Liouville fractional derivativeof order α>0 are defined by


and respectively,where m−1< α ≤ m,m ∈ N+,and Γ(·)denotes the Gamma function.
Of course,one has to impose some conditions on the function x such that the right hand sides are defined for almost all t∈ [a,b].For example,the fractional integralis defined for x∈L1(a,b).
The Laplace transform of the Riemann-Liouville fractional derivative is given as follows:

However,the practical applicability of the Riemann-Liouville fractional derivative is limited by the absence of the physical interpretation of the limit values of fractional derivatives at the low terminal t=0.The mentioned problem does not exist in the Caputo definition of the fractional derivative.
Definition 2.2([26]) Let[a,b]be a finite interval on the real axis R,and let x∈The Caputo fractional derivativeof order α>0 is defined by

The Laplace transform of the Caputo fractional derivative is given by
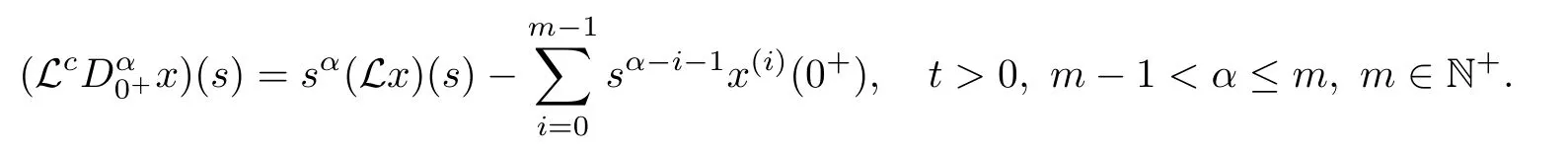
Contrary to the Laplace transform of the Riemann-Liouville fractional derivative,only integer order derivatives of function x appear in the Laplace transform of the Caputo fractional derivative.Thus,it can be useful for solving applied problems leading to linear fractional differential equations with constant coefficients with accompanying initial conditions in traditional form.
Particularly,the Riemann-Liouville fractional derivative and the Caputo fractional derivative are connected with the following relation
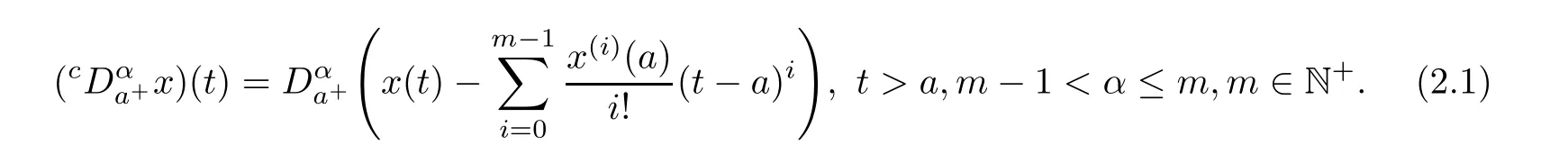
Note that if x(i)(a)=0,i=0,1,···,m − 1,thencoincides with
In this article,we consider the following semi-explicit nonlinear fractional differential algebraic system with two continuous inputs u and e:

In the following,we give sufficient conditions for the existence of nonnegative solutions of system(2.2)and construct a monotone waveform relaxation method to approximate the nonnegative solutions.For(2.2),the WR algorithm is described as
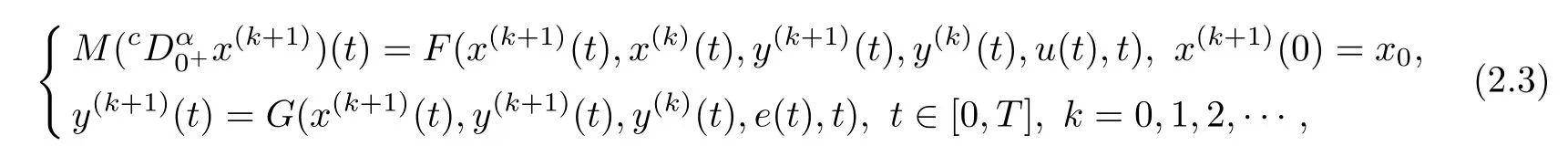

Definition 2.3Forfor all i=1,2,···,n.For x(t),y(t):for all t∈[0,T].
Definition 2.4A function h:Rn×Rm×R1→Rlis said to be globally Lipschitz continuous with respect to the first argument uniformly over the other arguments if there exists a constant L such that for all x,y∈Rn,e∈Rm,and t∈[0,T],kh(x,e,t)−h(y,e,t)kRl6 Lkx−ykRn,where k·kRland k·kRnare norms in Rland Rn,respectively.
Definition 2.5A function h:Rn×Rm×R1→Rlis said to be monotone increasing with respect to the first argument if for each e∈Rmand t∈[0,T],h(x,e,t)6 h(y,e,t)when x 6 y,where x,y∈Rn.A function k:Rn×Rm×R1→Rlis said to be quasi-monotone increasing with respect to the first argument if for each i∈ {1,2,···,n},each e ∈ Rm,and t∈ [0,T],ki(x,e,t)6 ki(y,e,t)when x 6 y with xi=yi,where x,y∈Rn.
Clearly,monotone increasing implies that quasi-monotone increasing.In fact,quasi-monotone increasing for functions is a key property used in proving the monotone convergence of iterative waveforms.This concept was carefully stated in[27].
In this article,except Theorem 3.2 of Section 3,we always assume that the functions F and G satisfy the following assumptions 1 and 2.
Assumption 1For all t ∈ [0,T],the function F(·,·,·,·,·,t)is globally Lipschitz continuous with respect to each of the first four arguments with Lipschitz constants Li(i=1,2,3,4),respectively,uniformly over the other arguments.Likewise,for all t∈[0,T],the function G(·,·,·,·,t)is globally Lipschitz continuous with respect to each of the first three arguments with Lipschitz constants Li(i=5,6,7),respectively,uniformly over the other arguments.
Assumption 2For all t ∈ [0,T],the function F(·,·,·,·,·,t)is quasi-monotone increasing with respect to the first arguments,and it is monotone increasing with respect to the each of the other four arguments.Likewise,for all t ∈ [0,T],the function G(·,·,·,·,t)is monotone increasing with respect to the each of the first four arguments.
Finally,we state an existence condition of solutions of system(2.2).This existence condition can be carried out by the approach in[24]with a careful modification on its proof.So,we omit the proof in this article.
Theorem 2.1Assume that for all t ∈ [0,T],the functions f(·,·,·,t)and g(·,·,·,t)are globally Lipschitz continuous with respect to each of the first two arguments with Lipschitz constantsand(i=1,2),respectively,uniformly over the other arguments,that is,for any u∈Rp,e∈Rq,xi∈Rn1,and yi∈Rn2(i=1,2,3,4),

and

Similarly,we give a convergence condition for the WR algorithm(2.3).
Theorem 2.2Assume that the functions F and G satisfy Assumption 1.If L7<1,then the iteration sequence{z(k)}produced by the WR algorithm(2.3)converges uniformly to the unique solution[x(t)T,y(t)T]Tof system(2.2)on[0,T].
3 Monotone Waveform Relaxation Method
3.1 Monotone dependency on initial conditions and inputs
We examine the monotone dependency properties on initial iteration and inputs for system(2.2)for any fixed k ∈ {0,1,2,···.}.These properties are useful to show the monotone convergence of the relaxation sequence based on system(2.2).For the sake of clarity,we consider the following nonlinear fractional differential-algebraic system for system(2.2)for some fixed k:
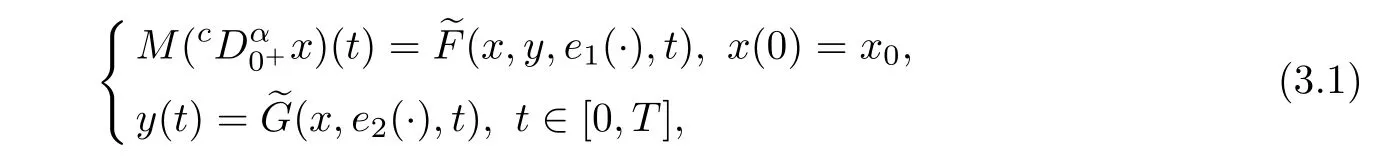
For system(3.1),let the inputs e1:[0,T]→ Rm1and e2:[0,T]→ Rm2be two given continuous functions.Then,we establish the following lemma.
Lemma 3.1Assume that for eachon t ∈ [0,T]when x>0,xi=0,and y>0.And assume that in system(3.1),on t∈ [0,T]when x>0.Then,the solution z(t)of system(3.1)satisfies z(t)>0 on[0,T]if the initial values subject to Mx0>0,and y(0)>0,where
ProofWe apply contradiction to show the statement.Suppose that there exist t∗>0 and some subscript l such that(Mx)l(t∗)<0 or yl(t∗)<0.Becauseis Lipschitz continuous with respect to x,system(3.1)has a unique solution and the solution depends continuously on the initial value and the right-hand continuous disturbance([26]).
Thus,there exists δ>0 such that the following system
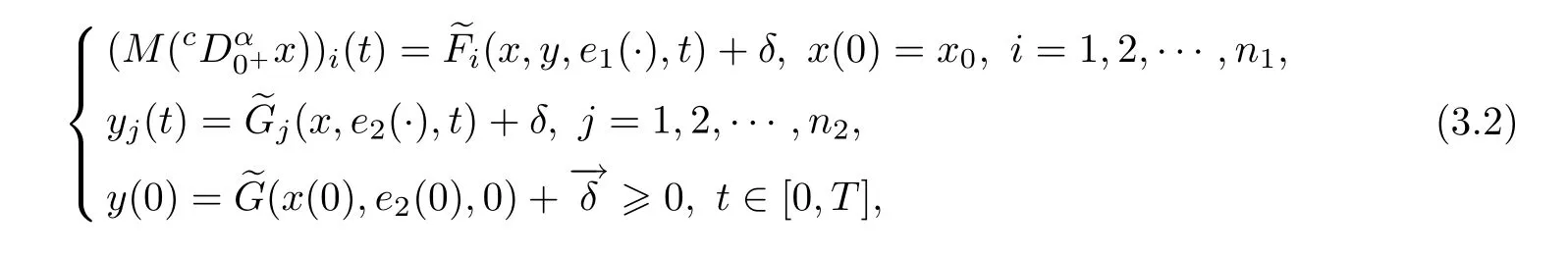
We denote z(t)=[x(t)T,y(t)T]T=[z1(t),z2(t),···,zn1(t),zn1+1(t),···,zn(t)],where n=n1+n2.Let K={k:zk(t)<0 for some t>0}and tk=inf{t>0:zk(t)<0}for k∈K.By continuity,zk(tk)=0 for each k∈K.Now,let r be the smallest integer such that tr=min{tk}.We have z(t)>0 for t 6 trin which zr(tr)=0.
Let r ∈ {1,2,···,n1}.When t 6 tr,it has x(t)>0,x(tr)=0,and x(t)<0 for t∈ (tr,tr+ǫ],ǫ is some positive constant.Then,by the Hadamard lemma(see[28],p.17),x(t)leads to the representation x(t)=(tr−t)h(t),with h(t)∈C1([0,tr]),h(t)>0 for t∈[0,tr],and h(t)6 0 for t∈ [tr,tr+ ǫ].

Then,it has
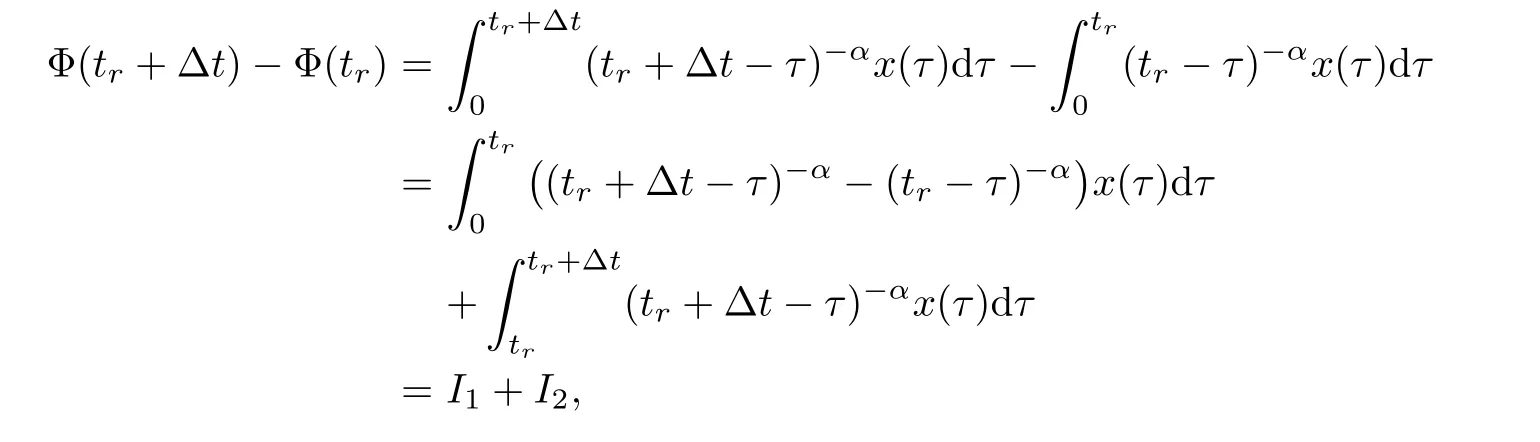
where
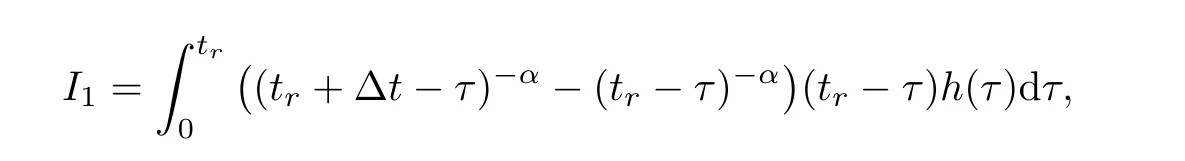
and

As h(t)is continuous on[0,tr]and the function

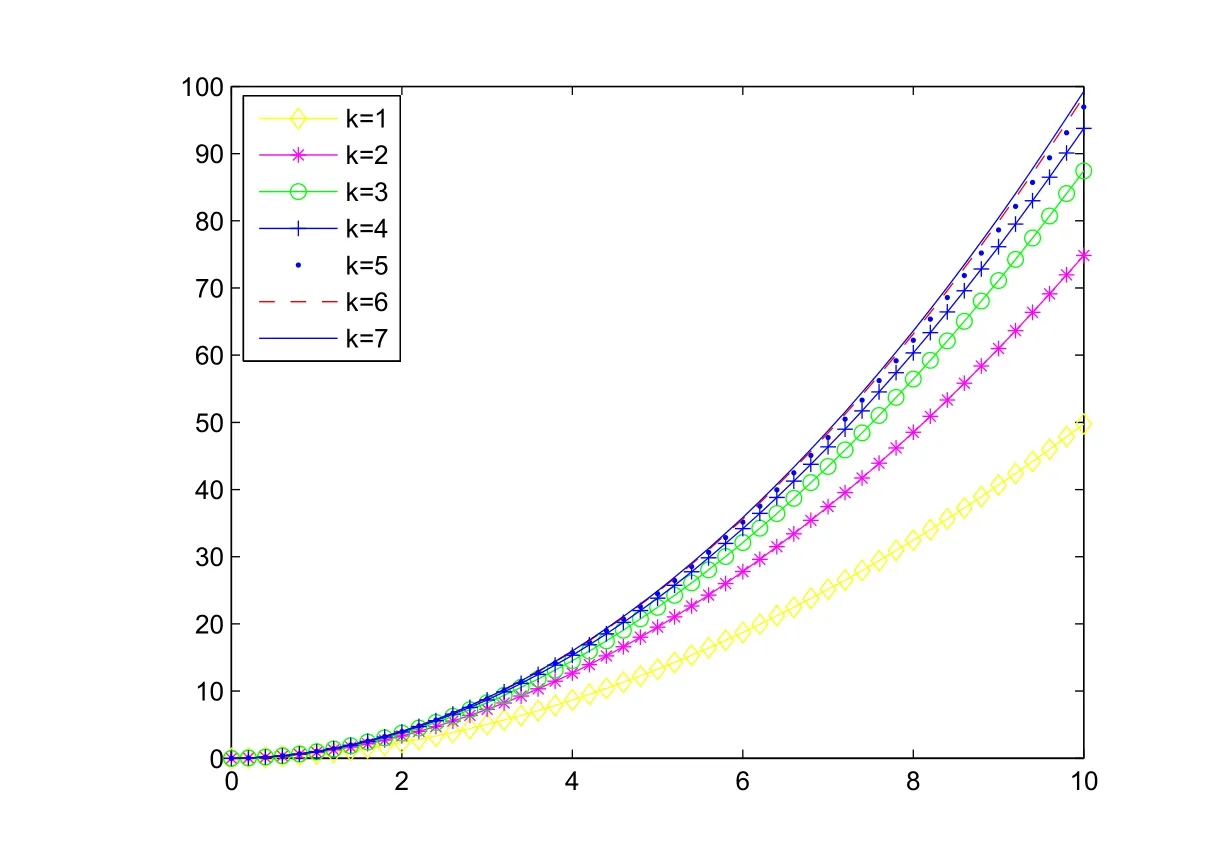
is of one sign and integrable on the interval[0,tr],the mean value theorem yields the following representation with a ξ,0< ξ It follows from the last representation that Because the function h is continuous and non-positive on[0,tr],the limitexists and is non-negative. Now,we consider the auxiliary functionthat is of one sign and integrable on the interval[tr,tr+∆t].Because the function h is continuous on[tr,tr+∆t],the mean value theorem applied to the integral I2yields the following representation with a ζ,tr<ζ Thus,we get the following representation On the basis of the relations(3.3)and(3.4),we can obtain Furthermore,by relation(2.1),we can obtain Let r∈ {n1+1,n2+2,···,n}.Then,yl(tr)=0,that is,Gl(x(tr),e2(tr),tr)+δ=0.This is impossible because x(tr)>0.This completes the proof of this lemma. ? In the following,we will discuss that for some fixed k,the iteration waveform at each iteration in the WR algorithm is monotonically dependent on the previous iterative waveform and input functions.For this aim,let,where x(k)(0)=x0is a solution of system(2.3)with given continuous input functions u,e,and the previous iterationAnd letwhereis a solution of system(2.3)with given continuous input functionsand the previous iterationLikewise,let z(t)=[x(t)T,y(t)T]T,where x(0)=x0is a solution of system(2.2)with given continuous input functions u and e.And letwhereis a solution of system(2.3)with given continuous input functions u and e.Under these conditions,we have the following result. Lemma 3.2Assume that the input functions in system(2.3)satisfy,and the(k−1)st iterations produced by the algorithm(2.3)satisfyingthen we haveon[0,T]if,and Likewise,assume that L7<1,and the input functions in system(2.2)satisfyandthen we haveon[0,T]if,and ProofThe two statements are analogous,so we consider the first.let η1(t)=x(k)(t) −Then,η1(t)and η2(t)satisfy the following system: Clearly,the functions of the right-hand sides of system satisfy the conditions of Lemma 3.1,so,we can arrive at η1(t)>0,and η2(t)>0 for all t ∈ [0,T],that is,[Mx(k)(t),y(k)(t)]>on[0,T]. By Theorem 2.2 and the first statement of this lemma,the second part is obvious.The proof of this lemma is completed. ? On the basis of the above statements,we can establish the existence theorem(Theorem 3.3)of nonnegative solutions of system(2.2).And from Theorem 3.1,one can see that the nonnegative solution of system(2.2)can be approximated using the WR algorithm(2.3)if the choice of initial iteration is proper. Theorem 3.1Suppose L7<1.If the initial iteration[(x(0)(t))T,(y(0)(t))T]Tin(2.3)satisfies and then,for each k∈N,it has ProofFrom by Lemma 3.2,one can obtain relation(3.7)for each k by induction.On the other hand,as L7<1,by Lemma 3.2,the sequenceconverges to[(x(t))T,(y(t))T]Tas k→+∞uniformly and monotonically on[0,T].This function[(x(t))T,(y(t))T]Tsatisfies From Theorem 3.1,we know that as long as the initial iteration is chosen properly,namely,x(0)(t)6 x(1)(t)and y(0)(t)6 y(1)(t)on[0,T],then the iterative procedure will monotonically converge to the actual solution of system. The choice of initial iterations is crucial to ensure monotone convergence of the waveforms in the WR algorithm.In the following,we present a choice to deal with this matter.In this subsection,we denote kxk∞=max{|xi|:i=1,2,···,n}for x ∈ Rn. For any given input functions u and e,we assume that and for xi∈ Rn1and yi∈ Rn2(i=1,2),where h1(·,·,·,·,t),and h2(·,·,·,t)are nondecreasing functions for any t∈[0,T]. Now,we need to assume that the following simple two-dimension fractional differential algebraic system has a positive solution w(t)=[w1(t),w2(t)]T: where x0is the given initial value and y0=g(x0,y0,e(0),0)in system(2.2). We define and Let and where t∈[0,T]and l=1,2.It is obvious that and Lemma 3.3Ifsatisfies ProofFirst,we define a sequencesuch that it satisfies and Thirdly,we need to prove that the sequenceconverges toas k→+∞on[0,T].In fact,we have and On the basis of the above relations,we have the following inequality where the operator Rcis defined by By[25],we have ρ(Rc)=0.Thus,we can derive ρ(R)=0,where This completes the proof of this lemma. The previous result says that if x(0)(t)is chosen as β1(t)and y(0)(t)is chosen as γ1(t),then x(0)(t)6 x(1)(t),and y(0)(t)6 y(1)(t)on[0,T].Thus,by Lemma 3.3 and Theorem 3.1,we can easily establish the following important result. Theorem 3.2Suppose L7<1,and let z(t)=[x(t)T,y(t)T]T,where x(0)=x0is a solution of system(2.2)with given continuous input functions u and e.Let the sequence{z(k)(t)}be defined by the WR algorithm(2.3)with initial iteration z(0)(t)=ρ1(t),where ρ1(t)is defined by(3.9).Then,the sequence{z(k)(t)}converges to the unique solution z(t)on[0,T],and the solution z satisfies that z(t)>0 for all t∈[0,T]. In this section,we give a simple example to con firm the monotone convergence properties of the WR algorithm for fractional differential-algebraic equations.In the processing of the numerical computation,the Caputo fractional derivative is computed by the implicit finite difference approximation: where xk=x(tk),and The time-step h is adopted as 0.2,and the error is defined bywhere x(k)is obtained by the WR algorithm,x is the true solution,and k·k denotes the 2-norm in Rn. Example 4.1Consider the following fractional differential-algebraic system: Its WR algorithm is described as One can see that the functions of the right-hand side in(4.2)satisfy Assumptions 1 and 2.Therefore,the sequenceobtained by equation(4.2)converges uniformly and monotonically to the solution of equation(4.1).From Figure 1,one can see that the nonnegative solution can be approximated by a monotone waveform sequence.The experiment results agree with the theory analysis. Figure 1 Monotone waveforms of x1in system(4.1) The errors are given in Table 1. Table 1 The relative errors for the different iterative numbers Appendix Hadamard’s lemmaAny smooth function f in a starlike neighborhood of a point z is representable in the form where giare smooth functions. In fact,by Hadamard’s lemma,any smooth function f(x)is representable in the form f(x)=f(x0)+(x−x0)g(x),where f(x0)=0,and g(x)is a smooth function.




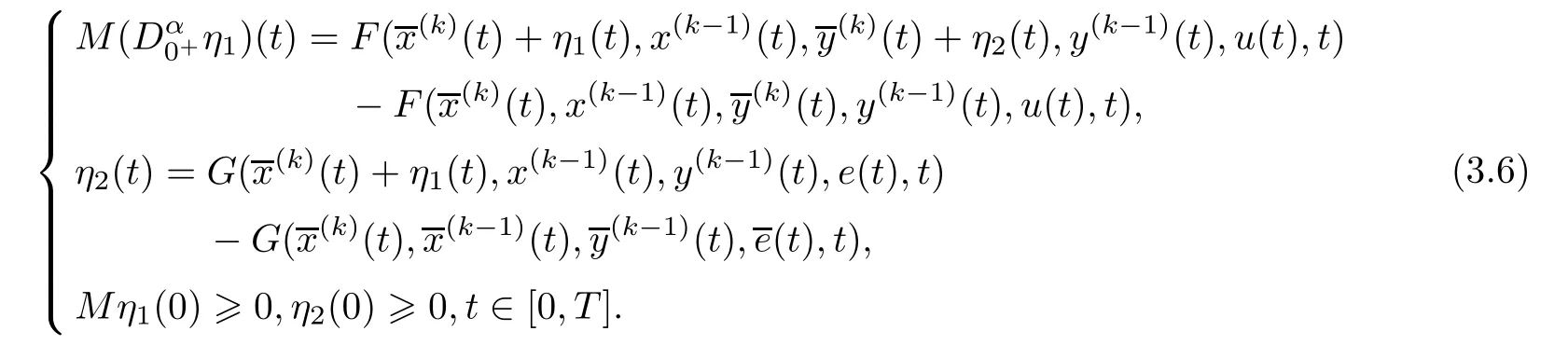
3.2 Convergence of monotone waveform relaxation

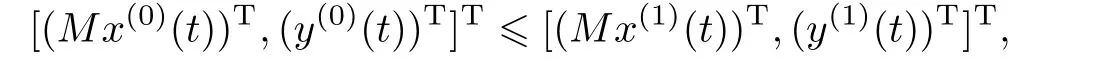
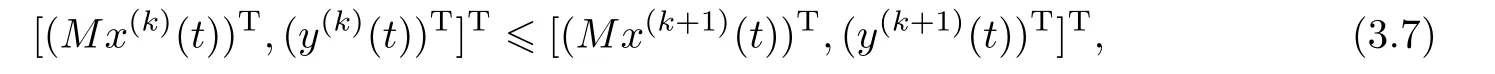


3.3 Initial iterations
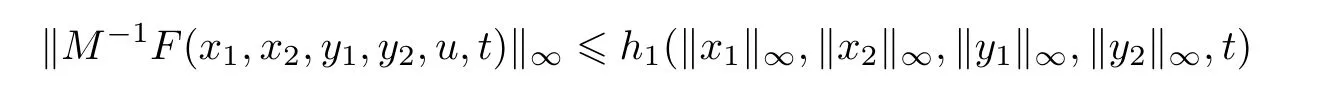



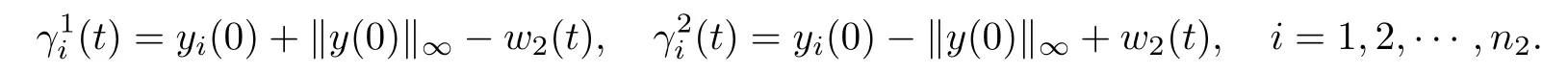
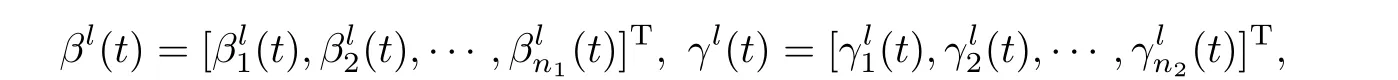



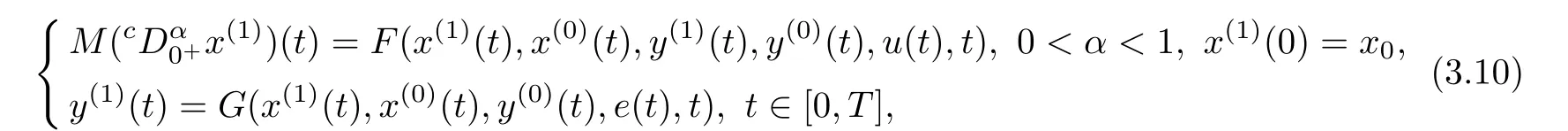



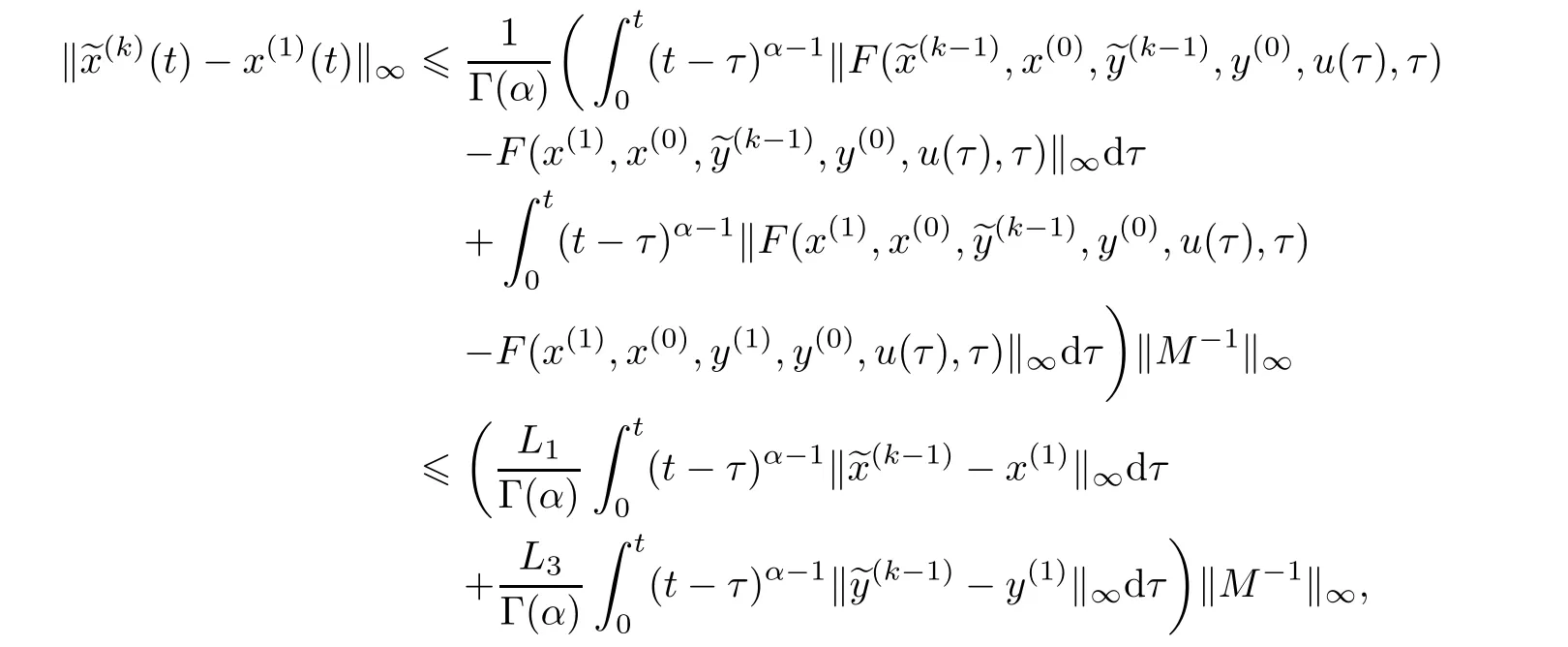




4 Example
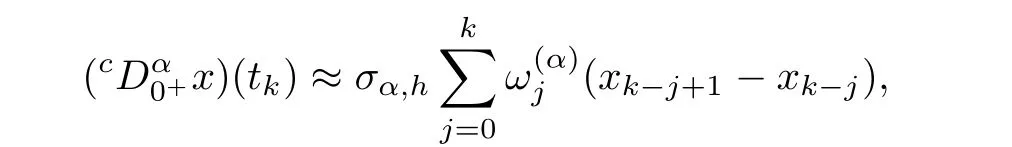


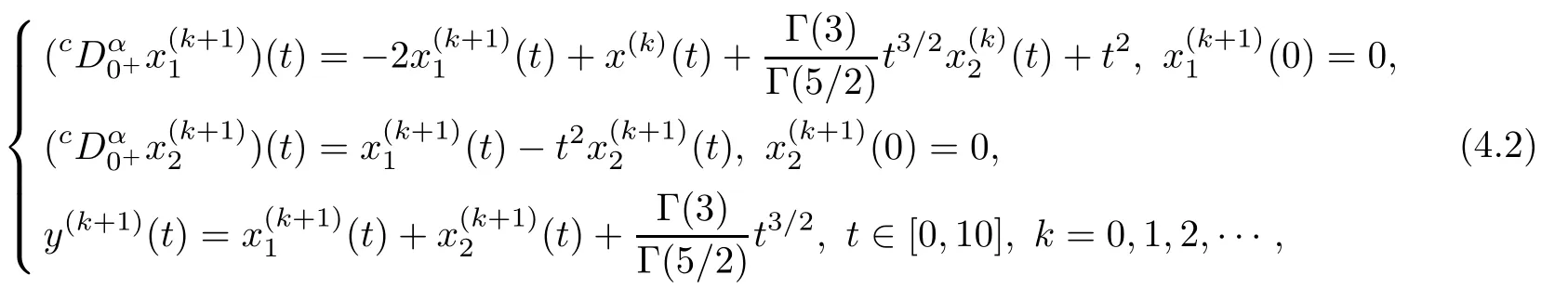


 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
