CONVERGENCE FROM AN ELECTROMAGNETIC FLUID SYSTEM TO THE FULL COMPRESSIBLE MHD EQUATIONS∗
Xin XU(徐鑫)
Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
E-mail:xuxinaboy@126.com
Abstract We are concerned with the zero dielectric constant limit for the full electromagneto- fluid dynamics in this article.This singular limit is justified rigorously for global smooth solution for both well-prepared and ill-prepared initial data.The explicit convergence rate is also obtained by a elaborate energy estimate.Moreover,we show that for the well prepared initial data,there is no initial layer,and the electric field always converges strongly to the limit function.While for the ill-prepared data case,there will be an initial layer near t=0.The strong convergence results only hold outside the initial layer.
Key words Zero dielectric constant limit;full compressible magnetohydrodynamic equation;initial layer
1 Introduction
When we consider the motion of an electrically conducting fluid in the presence of an electromagnetic field,the following system of electro-magneto- fluid dynamics is a commonly used system(cf.[1–3])
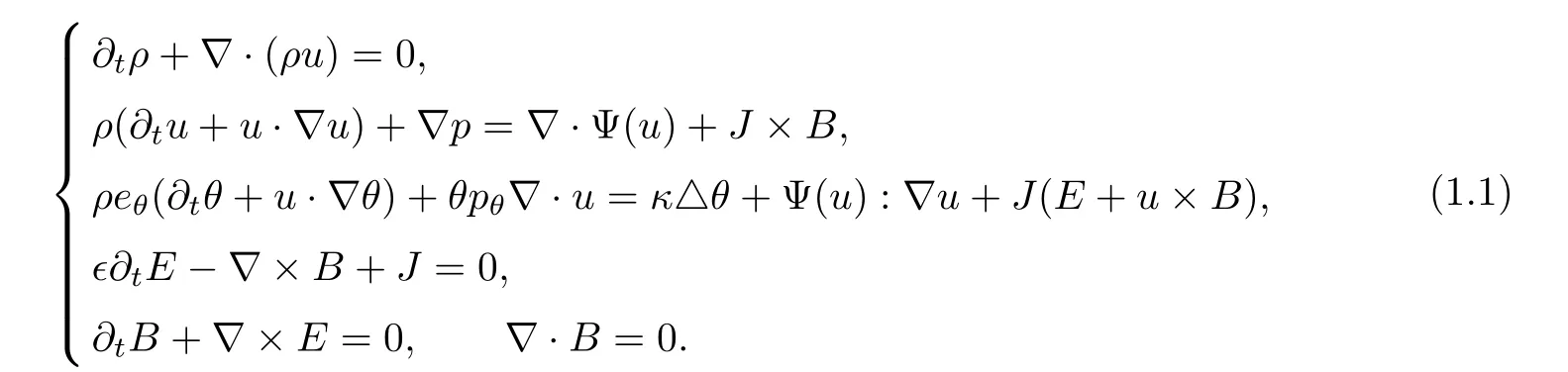
Here,ρ denotes the mass density,u=(u1,u2,u3)is the velocity,θ is the absolute temperature,E=(E1,E2,E3)is the electric field,and B=(B1,B2,B3)is the magnetic field.The pressure p and the internal energy e are expressed by the equations of state
All these quantities are functions of time t≥0 and position x∈R3.The viscous stress tensor Ψ(u)is given by
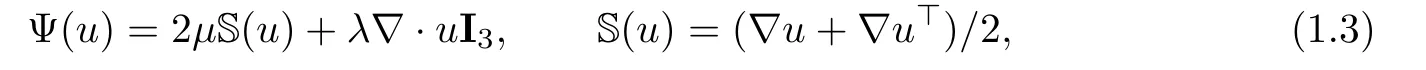
where I3denotes the 3×3 identity matrix,and∇u⊤the transpose of the matrix∇u.µand λ are the viscosity coefficients of the fluid which satisfiesµ >0 and 2µ+3λ >0.The electric current density J is given by Ohm’s law,that is,

where σ >0 is the coefficient of electrical conductivity.The second term Ψ(u): ∇u on the right-hand side of(1.1)3denotes the viscous dissipation function
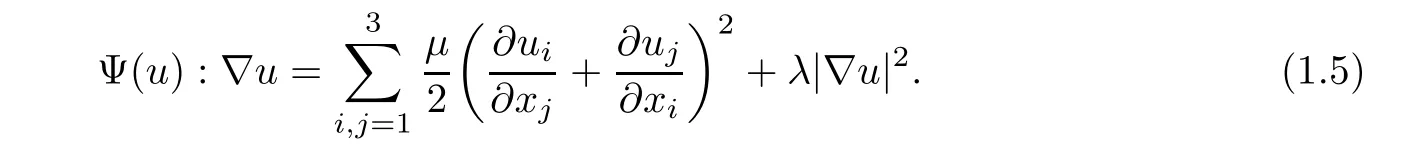
The coefficient of heat conductivity κ is assumed to be positive constant through this article.Finally,the positive number ǫ in the fourth equation of(1.1)is the dielectric constant.Generally,the dielectric constant is very small[2].In this article,we want to study the behavior of the solution for(1.1)when dielectric constant ǫ goes to zero.
Formally,if we let the dielectric constant ǫ=0 in(1.1);that is,the displacement current for the flow is negligible.Thanks to the fourth equation in(1.1),we have J=∇×B.Combining this with(1.4),we immediately haveThus,we can eliminate the electric field E by this equality in(1.1)and obtain the following system,

Obviously,this system is the classical full compressible magnetohydrodynamic equations and it has attracted a lot of attention in recent years because of its physical importance and mathematical challenges.Here,we only list some references from the perspective of mathematics for the interested readers.Concerning the well-posedness of compressible magnetohydrodynamic equations(1.6),we refer to[4–6]for the global existence of smooth solutions when the initial data are small perturbations of some constant state,[7,8]for the global existence of renormalized solutions for general large initial data with finite energy,and[9]for the existence of local strong solutions when the initial density contains vacuum.Singular limit problem(vanishing viscosity limit,low Mach number limit among others)for both isentropic and non-isentropic magnetohydrodynamic equation is another interesting question;see[10–12]for some recent result in this direction.There are also some other results concerning the blow-up criterions[13,14].
The above formal derivation is usually referred as magnetohydrodynamic approximation.We can see that the magnetohydrodynamic equations(1.6)are obtained as the limit of(1.1)at the vanishing of the dielectric constant.The mathematical study of this singular limit problem goes back to the initial work by Kawashima and Shizuta[15,16]who mainly considered the two spatial dimension case.More precisely,they rigorously justified this limit process for local large solution and global small solution.In a series of article[17–19],Jiang and Li proved local convergence for smooth solutions to the electromagnetic fluid system with and without viscosity in T3under the assumption that the initial data are well-prepared.In this article,we want to show that similar convergence holds globally in time for both well-prepared and ill-prepared data case as long as the initial data is sufficiently small.For convenience of presentation,we call(1.1)the full compressible Maxwell-Navier-Stokes equations,because it is the Navier-Stokes equations coupled with the Maxwell equations through the Lorentz force.It should be mentioned that the similar terminology was used by Masmoudi[20]for a different incompressible modeling system.
To emphasize the unknowns depending on the small parameter ǫ,we rewrite the electromagnetic fluid system(1.1)as

Initial data is given by
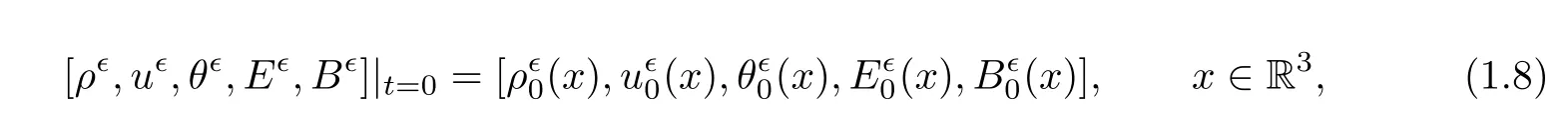
with the compatible condition

Obviously,for some positive constantand,(,0,,0,0)is a stationary solution of(1.7).For the global existence of the above Cauchy problem,we have the following theorem,which has been established in our previous work[21].
Theorem 1.1([21])Assume that for each ǫ∈(0,1]and s≥3,HsandThen,there exists a constant δ1>0 and C1>0,such that if

the Cauchy problem(1.7)admits a unique global solutionwhich satisfies

for any t≥0.
Similarly,we rewrite the limiting equations(1.6)as
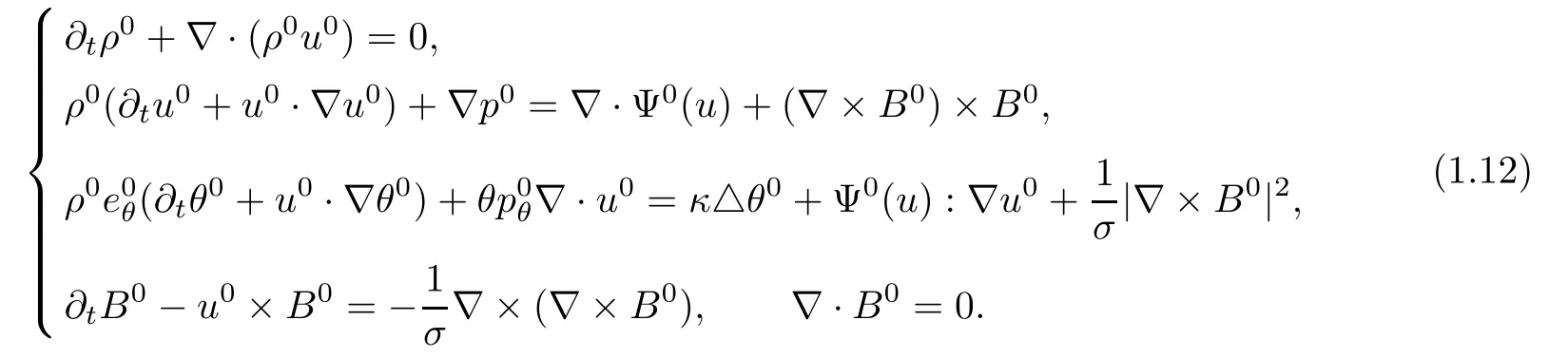
The above system is completed with the initial conditions

The compatible condition

is also needed here.We define
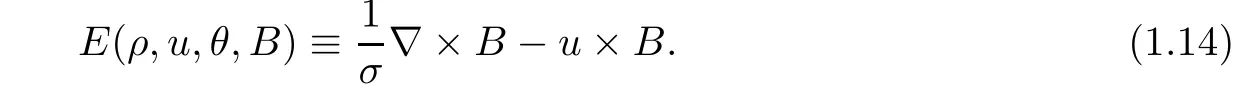
Moreover,we introduce the following notation:

Theorem 1.2There exists a constant δ0,such that if

the solution[ρǫ,uǫ,θǫ,Eǫ,Bǫ]established in Theorem 1.1 converges to a function[ρ0,u0,θ0,E0,B0]on[0,T]× R3as ǫ goes to zero,where T is an arbitrary fixed time.The limit function[ρ0,u0,θ0,B0]is the unique solution of(1.12)with initial data[ρ0,u0,θ0,B0](0,x)=And the following equality
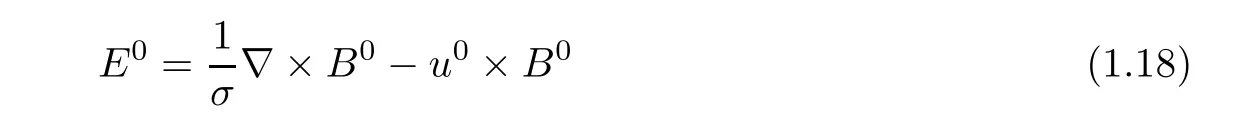
also holds for the limit function.Moreover,for t∈ [0,T]and ǫ∈ (0,1],we have the following estimate

where η =max{1−2β,1−2γ}.
Furthermore,for both well-prepared data and ill-prepared data,we want to study the strong convergence of the electric field.The following theorem is our second main result.
Theorem 1.3(i)When β>0 in(1.15),that is the well-prepared data case.Then,we have Eǫ→E0strongly in L∞([0,T];H2(R3)).
(ii)When β=0 in(1.15),that is the ill-prepared data case.Then,there exists a small constant κ >0,such that for t∗= ǫ1−κ,we have Eǫ→ E0strongly in L∞([t∗,T];H2(R3)).
Remark 1.4We can see from Theorem 1.3 that,in the ill-prepared initial data case,the convergence can not be uniformly in time;this is because of the presence of the initial layer near t=0.And κ >0 implies the thickness of this initial layer is O(ǫ).
The rest of this article is arranged as follows.In Section 2,we will give some sharp estimate to the solution which will be useful to the proof of the main theorems.In Section 3,the limit process is rigorously proved by combining the crucial estimate in Section 2 and energy method.The last section is devoted to the analysis of the initial layer and strong convergence of the electric field.
For the later use in this article,we give some notations.C denotes some positive genetic constant.or simplywith multi-index α stands for the usual spatial derivatives. ∇lwith an integer l≥0 stands for any spatial derivatives of order l.For any integer s≥0,Hsdenote the inhomogeneous Sobolev space Hs(R3).We denote k·kHsby k·ksfor simplicity.Set L2=H0and denote k·k=k·kL2for simplicity.We use hf,gi denote the L2inner product of f and g,namely,
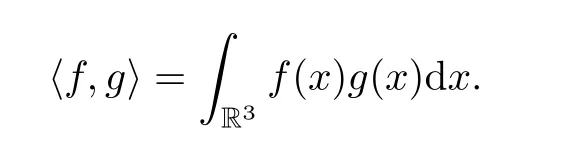
Moreover,for two operators A and B,[A,B]=AB−BA is the commutator.
2 Estimate for Time Derivative
In this section,we shall establish some sharp estimates of the solution and these estimates are useful in the next section.Our main purpose in this part is to establish the following theorem.
Theorem 2.1Under the assumptions of Theorem 1.1,then there exists a positive constant δ2(≤ δ1)and C2>0,such that if

the solution established in Theorem 1.1 satisfies the estimate
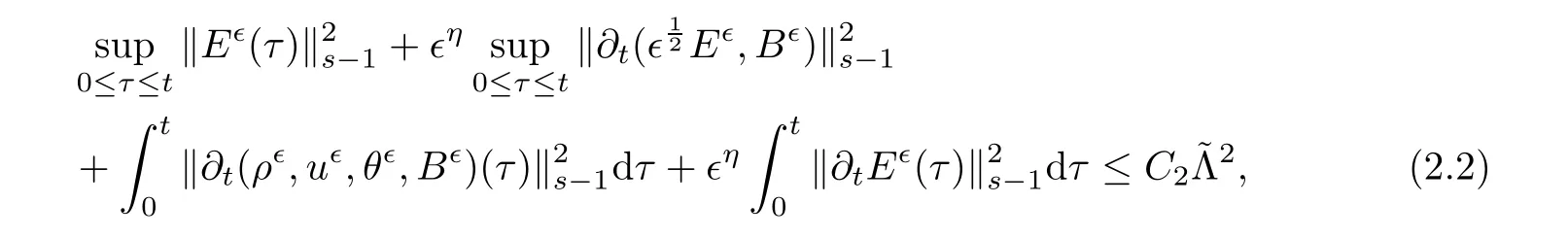
for any t≥ 0,where η =max{1−2β,1−2γ}.
ProofFrom estimate(1.11)in Theorem 1.1 and original system(1.7),we immediately have

Taking time-derivative to the last two equations in(1.7)yields

with

Then,by a direct energy estimate,we have

where estimate(2.3)is used.From the fourth equation in(1.7)and assumption(2.1),we have

and

Combining(2.6)and(2.7)-(2.8)gives

Denoting η=max{1−2β,1−2γ},clearly,we have 1≥η≥0.Recall≡Λ1+Λ2+Λ3,then(2.9)leads to

Furthermore,because of the fact η ≤ 1,we get
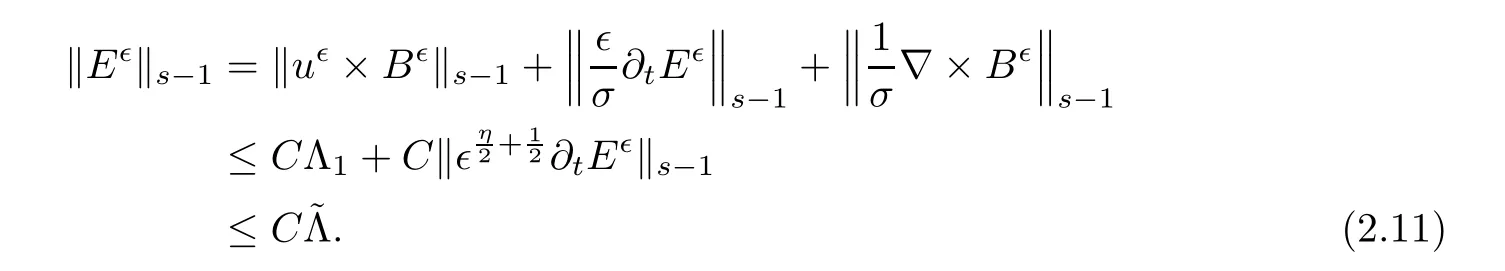
As a result,substituting(2.11)into(2.3)gives

Finally,(2.2)is proved by combining(2.3),(2.10),and(2.12).This complete the proof of Theorem 2.1. ?
3 Zero Dielectric Constant Limit
We will study the zero dielectric constant limit of the solution constructed in Theorem 1.1 in this section.In other word,we need to prove the convergence of the sequence(ρǫ,uǫ,θǫ,Eǫ,Bǫ)as ǫ→ 0.
Let 0≤ δ≤ ǫ,and denote

Then,from(1.7),we can see thatsatisfy the following equation

where the source terms are given by
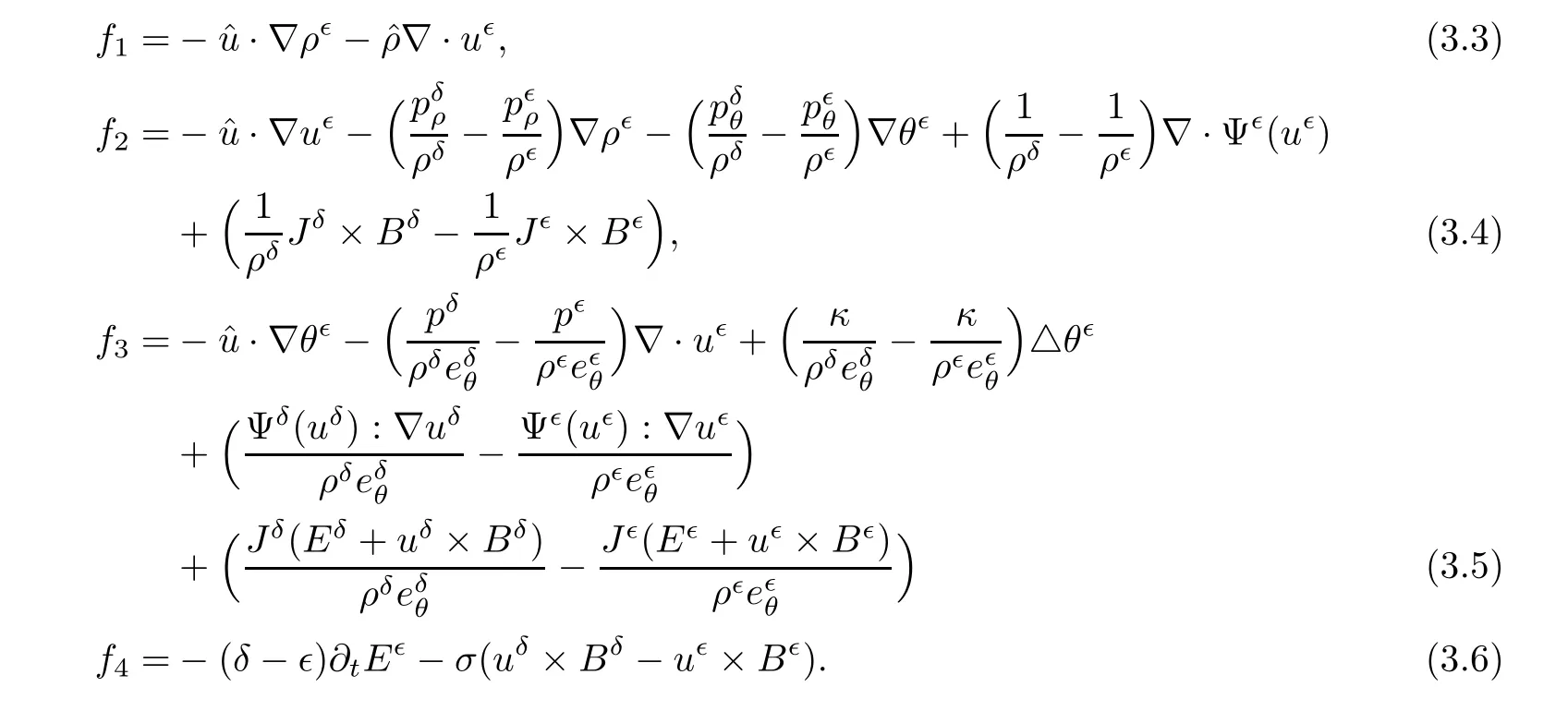
Proposition 3.1If the assumptions of Theorem 1.2 hold,then we have the following estimate

ProofApplyingwith 0 6|α|6 s−1 to equations(3.2)and multiplying them byrespectively,integrating over R3,then adding them up,we have
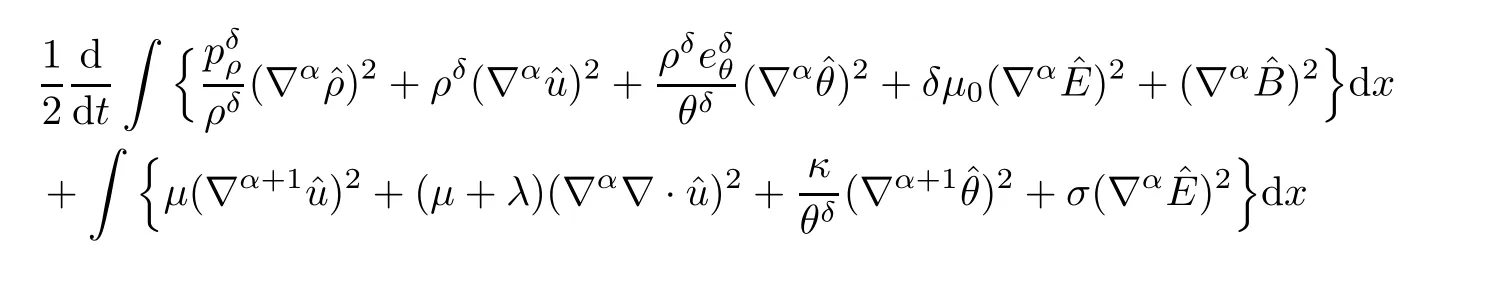

with
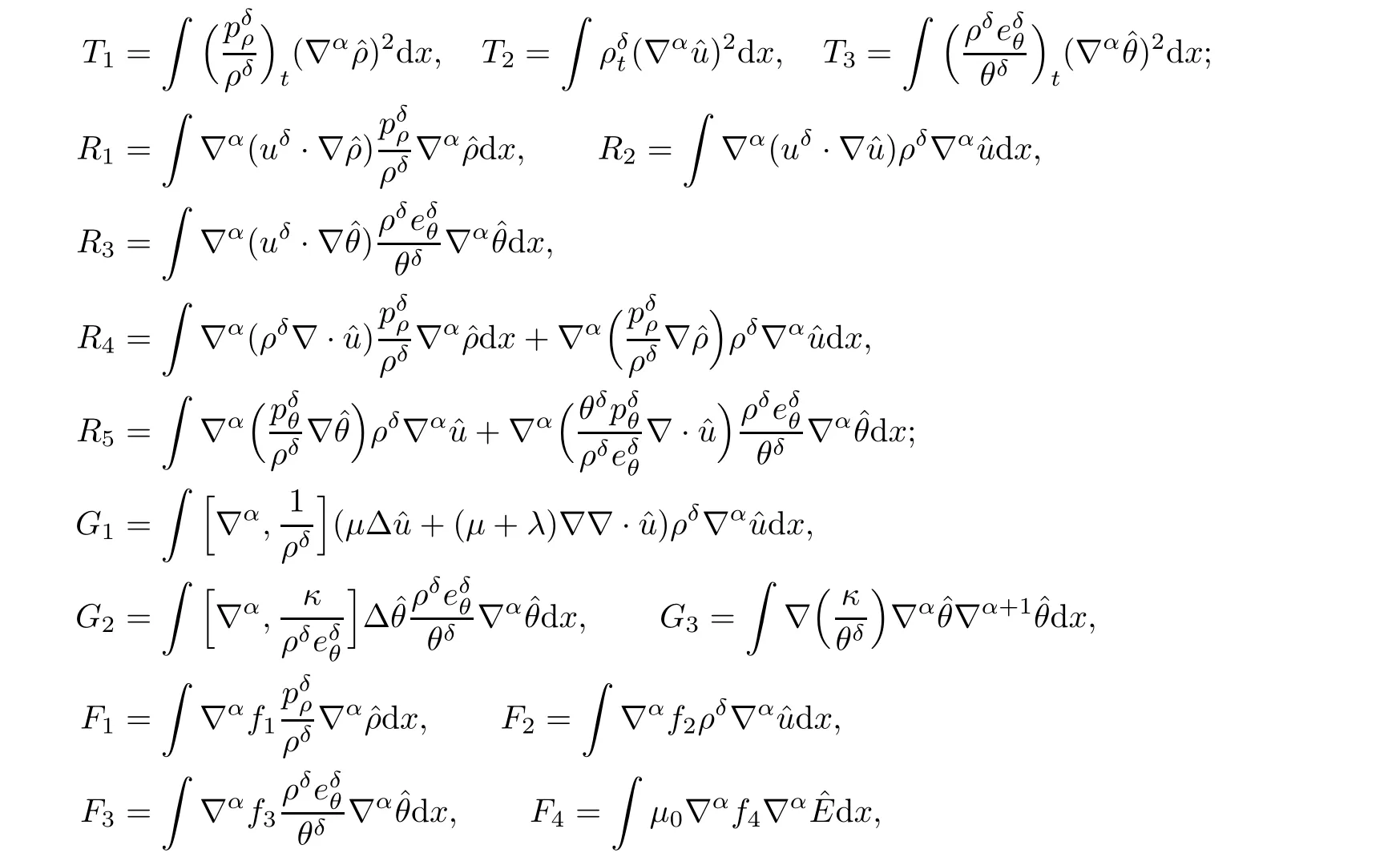
where[,]represent the commutator.Now,we need to estimate each term in the right-hand side of(3.8).For the estimate of Ti,we have

Next,we will give the estimate of Ri.Actually,we have
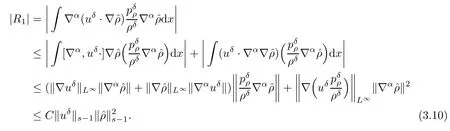
The estimate of R2and R3is similar,so we omit the details.

For the estimate of R4and R5,we need to use its symmetric property.First,R4can be estimated as


Similarly,we have

Now,we need to estimate G1,G2,and G3,respectively.For G1,we have

where ε is a small constant and the Cauchy-Schwartz inequality is used.Similar to the estimate of G1,we can estimate G2as follows

We can also estimate G3as

Finally,we only need to give the estimate of Fi.To this end,we need the following lemma which concerns the estimate of fi.
Lemma 3.2For 0 ≤ |α|≤ s−1,we have the estimates
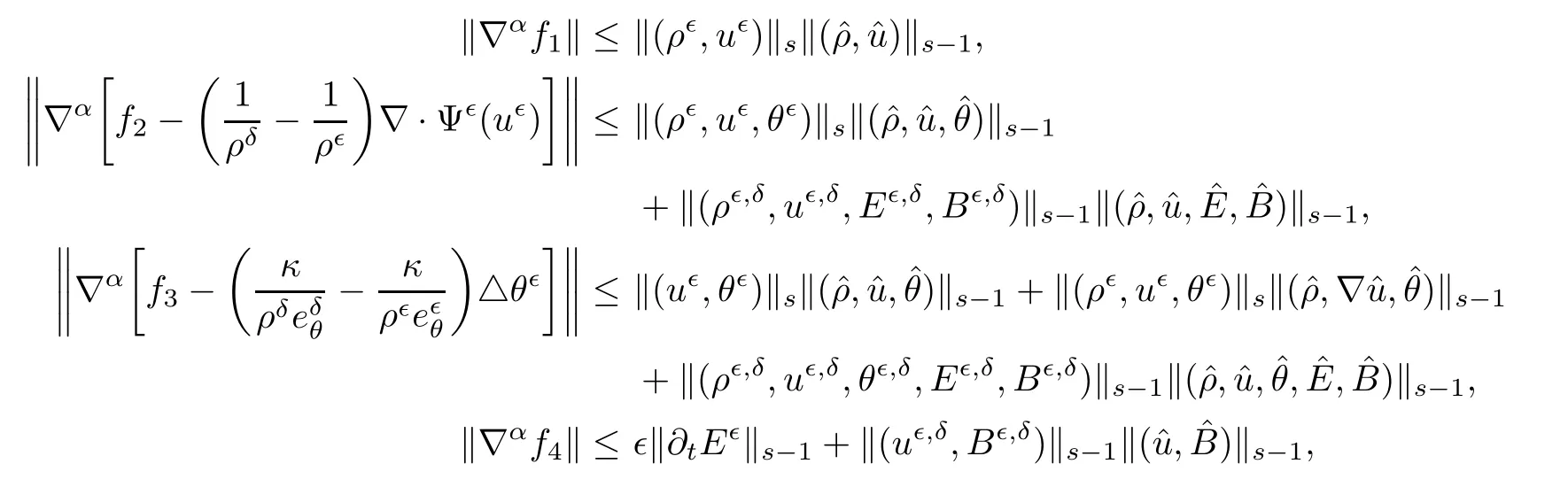
where Aǫ,δrepresents(Aǫ,Aδ).
We postpone the proof of this lemma to the end of this section,and we continue the proof of Proposition 3.1.By Lemma 3.2,we can estimate Fias
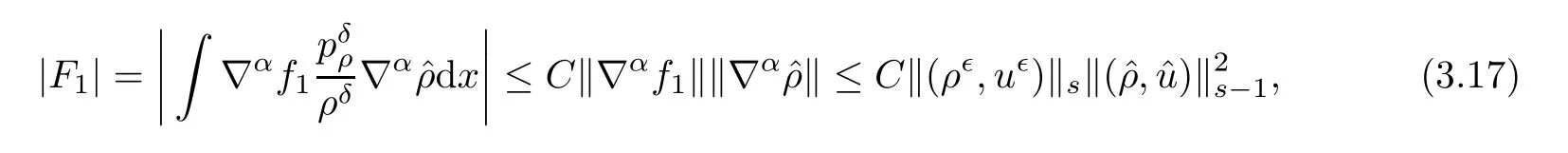
and

Similarly,the following estimate on F3holds
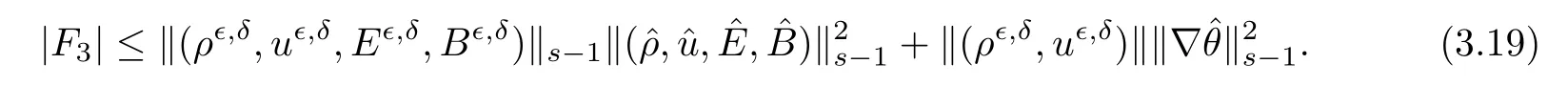
For F4,one has

Denote
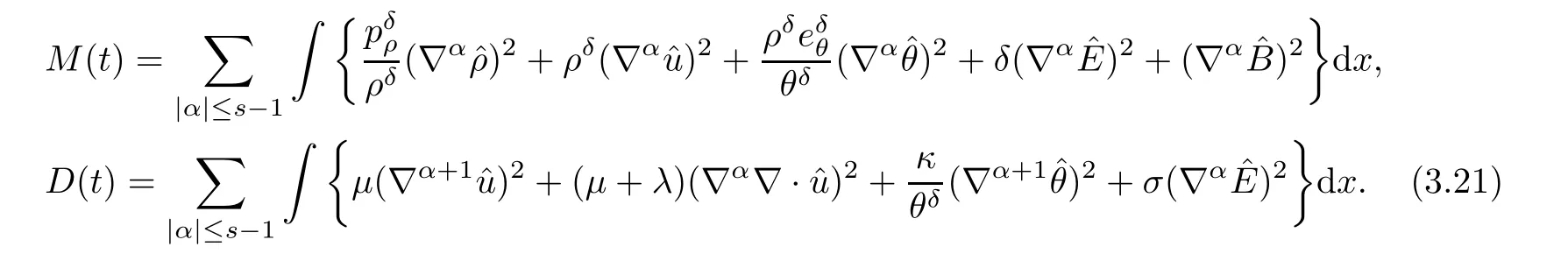
As a result,

By Gronwall inequality,we have
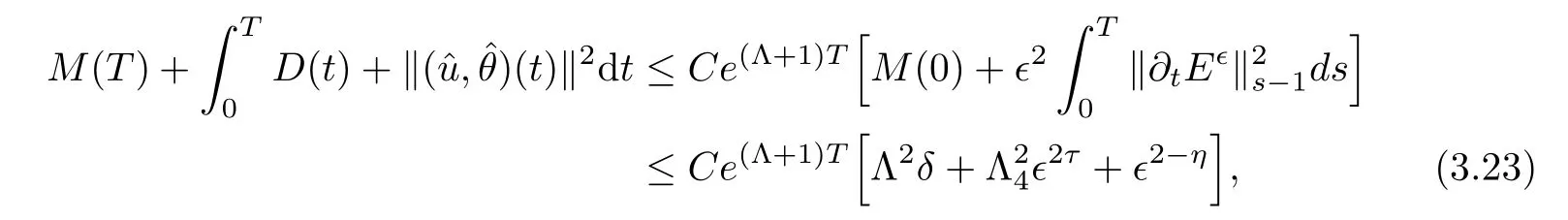
where we have used the fact that

Thus,this completes the proof of Proposition 3.1. ?
On the basis of the estimate in Proposition 3.1,we can give the proof of our main theorem.
Proof of Theorem 1.2For any fixed time T>0,let ǫ→ 0 in estimate(3.7)of Proposition 3.1,we can see

As a result,there exists a unique function(ρ0,u0,θ0,E0,B0)satisfying

And as ǫ→ 0,we have the following convergence result:
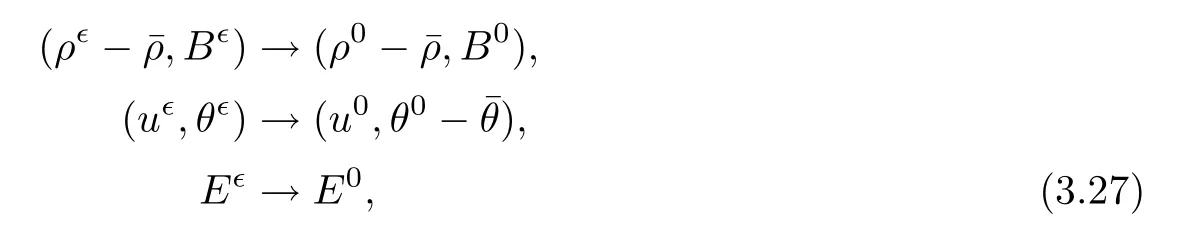

also holds.Finally,the convergence rate can be easily obtained from(3.7)by letting δ goes to zero.That is

Thus,we complete the proof of Theorem 1.2.?
Finally,let us give the proof of Lemma 3.2.
Proof of Lemma 3.2For the estimate of∇αf1,by direct calculation,we can see that For∇αf2,we have

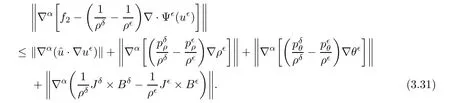
Now,denote the right-hand side term of(3.31)by giwith i=1,2,3,4.Let us give the estimate of each term.Firstly,we have

For g2,we can use the Taylor formula to get

where C(pρρ,ρδ,ρǫ)is bounded from below and above by some constants.Similarly,it holds that

For the estimate of g4,we need to rewrite it into
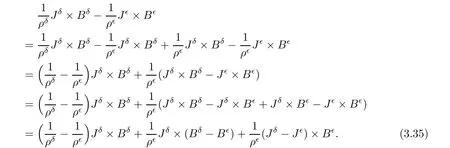
Notice that

Thus,from(3.35)–(3.36),we can estimate g4as
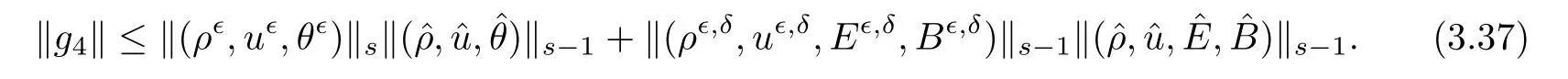
Collecting the estimate of(3.32)–(3.37),we get the estimate of f2.And the estimate for f3is similar,so we omit it for simplicity.Finally,the estimate of f4is easy because

Thus,we complete the proof of Lemma 3.2.
4 Initial Layer Analysis
In this section,we want to give a detailed analysis to the initial layer when the initial data is ill-prepared.We show that when the initial data is well-prepared,there is no initial layer,hence the solution will converge strongly to the limit function.While for ill-prepared initial data,an initial layer will appear,and the strong convergence for electric filed holds only outside the initial layer.
Now,we introduce
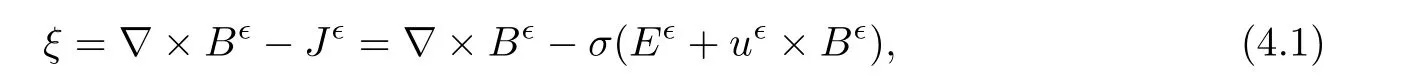
then it follows from equation(1.7)that

Taking one derivative to(4.1)with respect to t yields
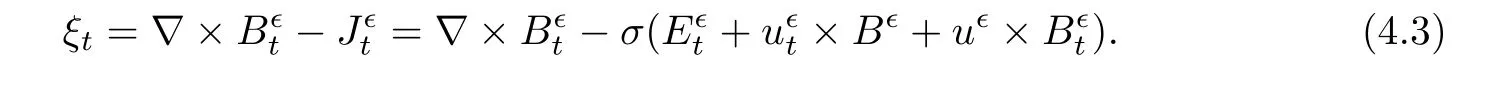
Thus,

Denote the right-hand side of(4.4)by M.Then,a direct energy estimate to(4.4)gives

Using Cauchy-Schwarz inequality to(4.5),we get

Combining estimate(2.2)in Theorem 2.1 and equation(1.7),we can see that

From(4.6)and(4.7),we get

Solving(4.8)
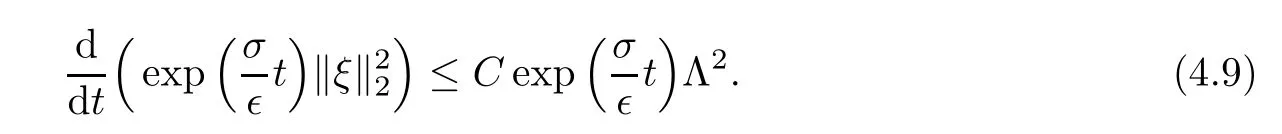
That is
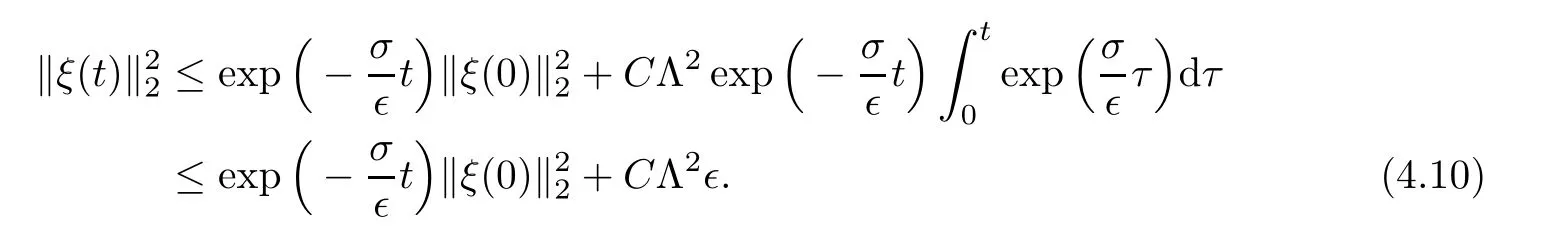
Now,for the well-prepared initial data,this is,β>0 in(1.15),we have

Putting(4.11)into(4.10)gives


That is Eǫconverge to E0strongly in L∞(0,T;H2).While for the well-prepared initial data,that is,β=0 in(1.15),we only have

Obviously,the similar strong convergence results can not be expected to hold near t=0.However,we can prove that after a small time,we will have the strong convergence.Actually,from(4.10),we have

Now,we choose t∗=Cǫ1−κfor a small constant κ >0.Then,for t≥ t∗,we can get

Substituting(4.16)into(4.15),we get

Similar to the estimate of(4.13),we can show that Eǫconverge to E0strongly in L∞(t∗,T;H2).Collecting the argument in this section,we have proved Theorem 1.3.
 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
- Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL EXISTENCE OF CLASSICAL SOLUTIONS TO THE HYPERBOLIC GEOMETRY FLOW WITH TIME-DEPENDENT DISSIPATION∗
- NONNEGATIVITY OF SOLUTIONS OF NONLINEAR FRACTIONAL DIFFERENTIAL-ALGEBRAIC EQUATIONS∗
- GROWTH AND DISTORTION THEOREMS FOR ALMOST STARLIKE MAPPINGS OFCOMPLEX ORDER λ∗
- EXACT SOLUTIONS FOR THE CAUCHY PROBLEM TO THE 3D SPHERICALLY SYMMETRIC INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
- PRODUCTS OF RESOLVENTS AND MULTIVALUED HYBRID MAPPINGS IN CAT(0)SPACES∗
- ON ENTIRE SOLUTIONS OF SOME TYPE OF NONLINEAR DIFFERENCE EQUATIONS∗
