PRODUCTS OF RESOLVENTS AND MULTIVALUED HYBRID MAPPINGS IN CAT(0)SPACES∗
Gholamreza ZAMANI ESKANDANI Soheila AZARMI Masoumeh RAEISI
Department of Pure Mathematics,Faculty of Mathematical Sciences,University of Tabriz,Tabriz,Iran
E-mail:zamani@tabrizu.ac.ir;s.azarmi2008@gmail.com;m.raeisi@tabrizu.ac.ir
Abstract In this article,we introduce and investigate the concept of multivalued hybrid mappings in CAT(0)spaces by using the concept of quasilinearization.Also,we present a new iterative algorithm involving products of Moreau-Yosida resolvents for finding a common element of the set of minimizers of a finite family of convex functions and a common fixed point of two multivalued hybrid mappings in CAT(0)spaces.
Key words Multivalued hybrid mappings;convex optimization;CAT(0)spaces
1 Introduction
Let H be a Hilbert space and let C be a nonempty closed convex subset of H.Then,a mapping T:C→C is said to be nonspreading if

for all x,y∈C.Recently,Iemoto and Takahashi[1]showed thatis nonspreading if and only if

for all x,y∈C.Furthermore,Takahashi[2]defined a class of nonlinear mappings which is called hybrid as follows:
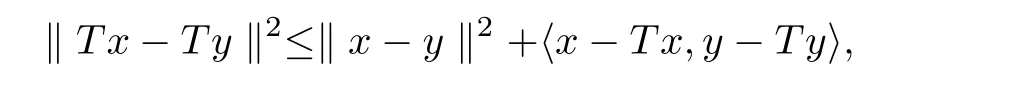
for all x,y∈C.It was shown that a mapping T:C→H is hybrid if and only if

for all x,y∈C.So,a hybrid mapping T:C→H is different from a nonspreading mapping.
Let C be a subset of a CAT(0)space X.We denote by CB(C)and K(C)the collection of all nonempty closed bounded subsets and nonempty compact subsets of C,respectively.The Hausdor ffmetric H on CB(X)is defined by for all A,B∈CB(X),where d(x,B)=inf{d(x,z):z∈B}.

Let T:X→2Xbe a multivalued mapping.An element x∈X is said to be a fixed point of T,if x∈Tx.The set of its fixed points will be denoted by F(T).
Very recently,Cholamjiak et al[3]defined a class of multivalued mappings in Hilbert spaces,which is called multivalued hybrid mappings,as follows:

for all x,y∈C,also they introduced an iterative process for the approximation of a common fixed point of a finite family of multi-valued hybrid mappings Ti:C→K(C)as follows:
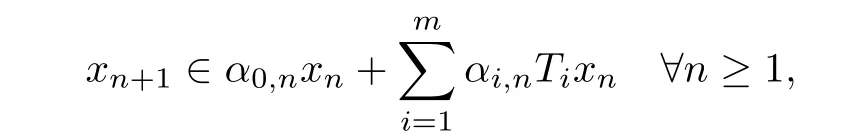
and under certain appropriate conditions,they proved that the sequence{xn}∆-converges to a common fixed point of{Ti}.
The study of metric space X without linear structure has played a vital role in various branches of pure and applied sciences.In particular, fixed point theorems in CAT(0)spaces for nonexpansive single valued,as well as for multivalued mappings,were studied extensively by many authors[4–10].
Let f:X → (−∞,∞]be a proper and convex function.One of the major problems in optimization is to find x∈X such that

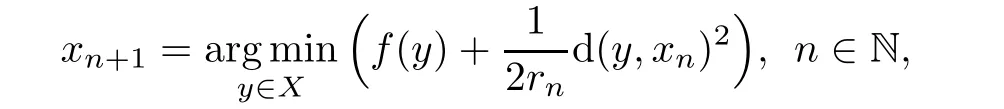
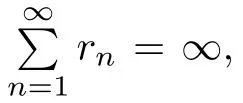
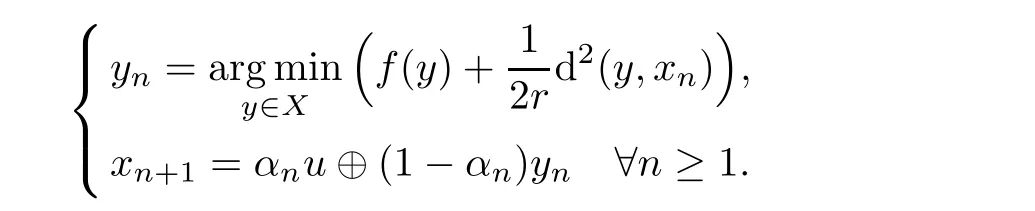
Under suitable condition on parameters,he proved that the sequence{xn}converges strongly to a minimizer of f(see also[18,19]).
Multivalued nonexpansive mappings have nontrivial applications in pure and applied science.Examples of such applications are in control theory,convex optimization,differential inclusions,game theory,and economics[20].Recently,many convergence results by the PPA for solving optimization problems were extended from the classical linear spaces to the setting of Reimannian and Hadamard manifolds[21,22].Numerous applications in computer vision,machine learning,electronic structure computation,system balancing,and robot manipulation can be considered as solving optimization problems on manifolds(see[23–25]).As Hadamard manifolds and Hilbert spaces are two special cases of Hadamard spaces,it is interesting to consider the proximal point algorithm and convex minimization in Hadamard spaces.
In this article,motivated and inspired by the above results,we introduce and investigate the concept of multivalued hybrid mappings in CAT(0)spaces by using the concept of quasilinearization.Also,using products of Moreau-Yosida resolvents,we present an iterative algorithm for finding a common element of the set of minimizers of a finite family of convex functions and a common fixed point of two multivalued hybrid mappings in CAT(0)spaces.
2 Preliminaries and Lemmas
Let(X,d)be a metric space.A geodesic path joining x to y in X is a mapping γ from a closed interval[0,l]⊆ R to X such that γ(0)=x,γ(l)=y,and d(γ(s),γ(t))=|s − t|for all s,t ∈ [0,l].In particular,the mapping γ is an isometry and d(x,y)=l.The image of γ is called geodesic segment joining x and y which is unique denoted by[x,y].We denote the unique point z∈[x,y]such that
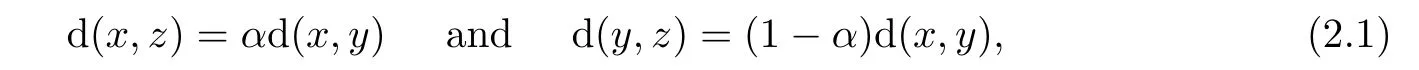

Using mathematical induction and[26,Proposition 2.2],it is easy to see that

The metric space(X,d)is called a geodesic space if any two points of X are joined by a geodesic,and X is said to be uniquely geodesic if there is exactly one geodesic segment joining x and y for each x,y∈X.A geodesic triangle△(x1,x2,x3)in a geodesic space(X,d)consists of three points in X(the vertices of△)and a geodesic segment between each pair of points(the edges of△).A comparison triangle for△(x1,x2,x3)in(X,d)is a trianglein the Euclidean plane R2such thatfor all i,j∈{1,2,3}.
A geodesic space X is called a CAT(0)space if all geodesic triangles of appropriate size satisfy the following comparison axiom:
Let△be a geodesic triangle in X and letbe a comparison triangle in R2.Then,the triangle△is said to satisfy the CAT(0)inequality if

for all x,y∈△and all comparison pointscomplete CAT(0)space is called an Hadamard space.A subset C of a CAT(0)space is convex if[x,y]⊆ C for all x,y∈C.It is well known that any complete simply connected Riemannian manifold of nonpositive sectional curvature is a CAT(0)space.Other examples include Pre-Hilbert spaces,R-trees(see[26]),Euclidean buildings,the complex Hilbert ball with the hyperbolic metric(see[20]),and many others.A geodesic space(X,d)is a CAT(0)space if it satisfies the(CN)inequality:

for all x,y,z∈X;see[27].
Let{xn}be a bounded sequence in a CAT(0)space X.For x∈X,we set

The asymptotic radius r(xn)of{xn}is given by r({xn})=inf{r(x,{xn}):x∈X},and the asymptotic center A({xn})of{xn}is the set

It is known that in a CAT(0)space,A({xn})consists of exactly one point[28].A sequence{xn}in a CAT(0)space X is said to be∆-convergent to x∈X if x is the unique asymptotic center of every subsequence of{xn}.In this case,we writeand call x the∆-limit of{xn}.Berg and Nikolaev in[29]introduced the concept of quasilinearization in a metric space X.Let us formally denote a pair(a,b)∈ X × X byand call it a vector.Then,quasilinearization is a mapdefined by:

for all a,b,c,d∈X.It is easily seen thatfor all a,b,c,d,x∈X.We say that X satisfies the Cauchy-Schwarzinequality if

for all a,b,c,d∈X.It is known[29]that a geodesically connected metric space is a CAT(0)space if and only if it satisfies the Cauchy-Schwarz inequality.
We will be using the following lemmas in the sequel.
Lemma 2.1([30]) Every bounded sequence in an Hadamard space has a∆-convergent subsequence.
Lemma 2.2([31]) If C is a closed convex subset of an Hadamard space and{xn}is a bounded sequence in C,then the asymptotic center of{xn}is in C.
Lemma 2.3([32]) If{xn}is a bounded sequence in an Hadamard space X with A({xn})={x}and{un}is a subsequence of{xn}with A({un})={u}and the sequence{d(xn,u)}converges,then x=u.
Let C be a nonempty subset of CAT(0)space X.Then,a mapping T of C into itself is called nonexpansive if d(Tx,Ty)≤d(x,y)for all x,y∈C.A point x∈C is called a fixed point of T if Tx=x.We denote by F(T)the set of all fixed points of T.Kirk[7]showed that the fixed point set of a nonexpansive mapping T is closed and convex.

Firmly nonexpansive mappings were first introduced by Browder[33],under the name of firmly contractive,in the setting of Hilbert spaces,and later by Bruck[34]in the context of Banach spaces.Recently,Bruck’s definition was extended to a nonlinear setting in[14](see also[8,15]).
Definition 2.5Let C be a nonempty subset of a CAT(0)space(X,d).We say that a mapping T:C−→X is firmly nonexpansive if
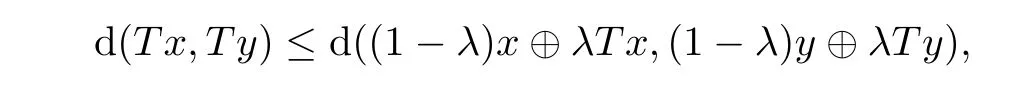
for all x,y∈C and λ∈(0,1).
Remark 2.6Any firmly nonexpansive mapping is nonexpansive.
The following theorem is a necessary condition for firmly nonexpansivity of T.
Theorem 2.7Let C be a nonempty subset of a CAT(0)space X and T:C−→X be a firmly nonexpansive mapping.Then,

for all x,y∈C.
ProofUsing(2.3)and firmly nonexpansivity of T,we get
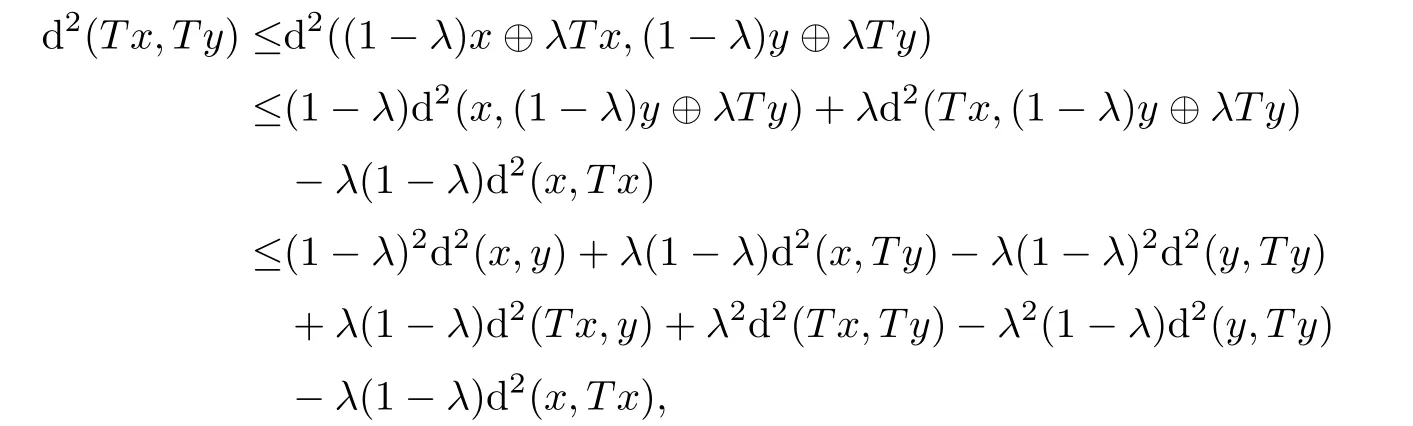
for all x,y∈ C and λ ∈ [0,1).Then,

So,
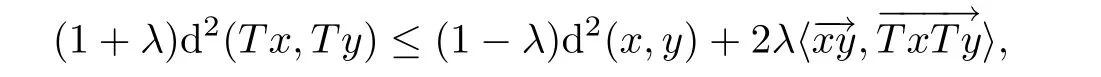
and when λ → 1,we obtain
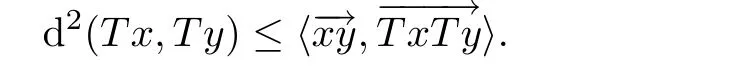
For λ>0,define the Moreau-Yosida resolvent of f in CAT(0)space(X,d)as

Recall that a function f:X −→ (−∞,+∞]defined on a convex subset D of a CAT(0)space is convex if,for any geodesic γ :[a,b]−→ C,the function f ◦ γ is convex.
The following lemmas play an important role in this article.
Lemma 2.8([14])Let(X,d)be an Hadamard space and f:X −→ (−∞,+∞]be a proper convex and lower semicontinuous function.Then,for every λ>0,it follows that
Lemma 2.9([35])Let(X,d)be an Hadamard space and f:X → (−∞,∞]be a proper convex and lower semi-continuous function.Then,the following identity holds:
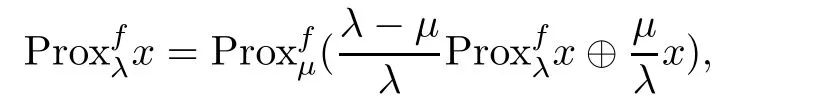
for all x∈X and λ>µ>0.
Let C be a nonempty closed convex subset of a CAT(0)space X.It is known that for any x∈X,there exists a unique point u∈C such that

The mapping PC:X −→C defined by PCx=u is called the metric projection from X onto C.
Lemma 2.10([13,Theorem 2.1.12])Let(X,d)be an Hadamard space and C be a nonempty closed convex subset of X.Then
(i)For every x∈X,there exists a unique point PC(x)∈C such that

(ii)If x∈X and z∈C,then

(iii)The mapping PC:X→C is nonexpansive.
Lemma 2.11([13,Proposition 3.1.3]) Let(X,d)be an Hadamard space.For a bounded sequence{xn}⊂X and x∈X,the following are equivalent:
(i)The sequence{xn}∆-converges to x;
(ii)For every geodesic γ:[0,1]→X with x∈ γ,we have Pγxn→ x as n→ ∞;
Using Lemmas 2.10 and 2.11,we can prove the following lemma.
Lemma 2.12Let(X,d)be an Hadamard space.If{xn}is a sequence in X which∆-converges to z∈X,then
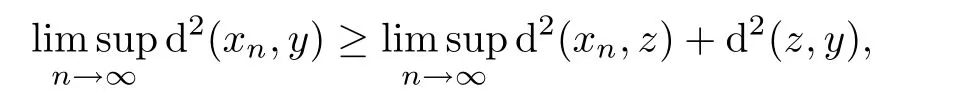
for all y∈X.
ProofFrom Lemma 2.10,we have


As{xn}is∆-convergent to z,by Lemma 2.11,we haveDefinition 2.13Let(X,d)be an Hadamard space and C be a closed convex subset of X.A multivalued mapping T:C→CB(C)is called
(i)Nonexpansive if H(Tx,Ty)≤d(x,y)for all x,y∈C;
(iii)Hybrid if

for all x,y∈C.
ExampleConsider X=[0,+∞)and C=[0,3]with the usual metric.The multivalued mapping T:C→CB(C)defined by
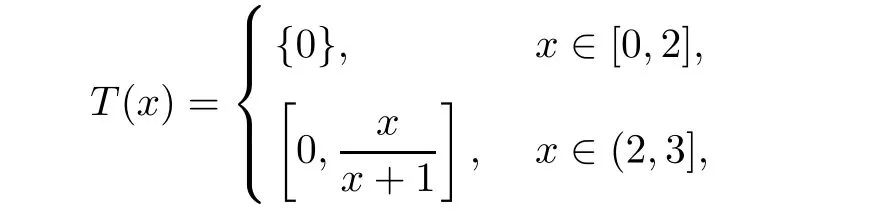
is a multivalued hybrid mapping,which is not nonexpansive[3].
3 Main Results
We present the following properties of a multivalued hybrid mapping in CAT(0)spaces by using the concept of quasilinearization.
Lemma 3.1Let C be a nonempty closed convex subset of an Hadamard space X and T:C→K(C)be a multivalued hybrid mapping.If x,y∈C and a∈Tx,then there exists b∈Ty such that

ProofLet x,y ∈ C and a ∈ Tx.From Nadler’s theorem[37],there exists b∈ Ty such that
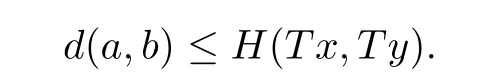
It follows that
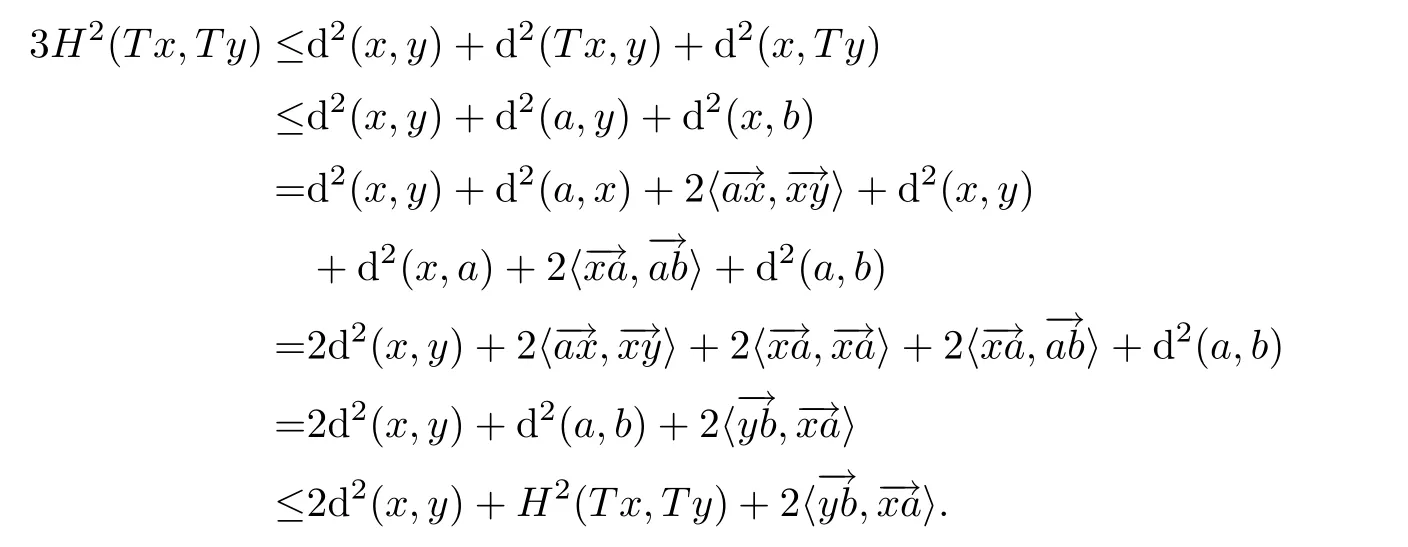
This implies that
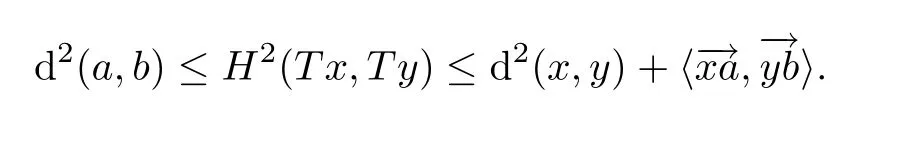
Lemma 3.2Let C be a nonempty closed convex subset of an Hadamard space X and T:C→K(C)be a multivalued hybrid mapping.Let{xn}be a sequence in C such thatfor some yn∈Txn.Then,p∈Tp.
ProofLet{xn}be a sequence in C such thatfor some yn∈Txn.Now,we show that p∈F(T).By Lemma 3.1,there exists zn∈Tp such that

As Tp is compact and zn∈Tp,there exists a subsequence{zni}of{zn}such that zni→z∈Tp.For each x∈X,define a function f:X →[0,∞)by

Then,by Lemma 2.12,we obtain
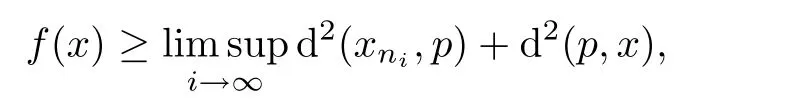
for all x∈X.Thus,f(x)≥f(p)+d2(p,x)for all x∈X.It follows that

Using Cauchy-Schwarz inequality,we get


Again using Cauchy-Schwarz inequality,we obtain

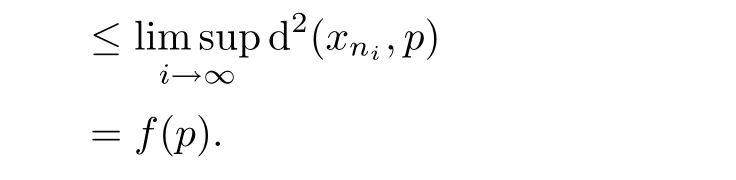
Then,f(z)≤f(p).From this and(3.2),we get d(p,z)=0.This completes the proof. ?
Lemma 3.3Let C be a nonempty closed and convex subset of an Hadamard space X and T:C→ K(C)be a multivalued hybrid mapping.Ifthen T is multivalued quasi-nonexpansive mapping.
ProofLet q∈F(T)and x∈C.By Lemma 3.1,there exists b∈Tx such that

This implies that H(Tq,Tx)≤d(q,x)for all x∈C and q∈F(T). ?
Now,we are in a position to introduce and prove∆-convergence theorem for the new iterative algorithm(3.3).
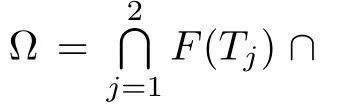
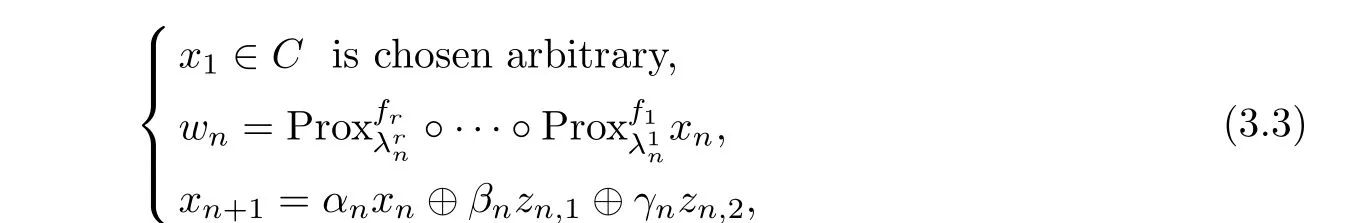
where zn,j∈Tj(wn),(j=1,2).Assume that the following conditions hold:
(i) αn+βn+γn=1,αn∈ [a,b]⊂ (0,1),βn∈ [c,1)⊂ (0,1),γn∈ [d,e]⊂ (0,1),n ∈ N.
ProofLet q∈ Ω.It follows from Lemma 2.8 thatfor any i=1,···r and n∈N.We show thatexists.Denote bythe compositionfor any i=1,2,···,r and n ∈ N.Therefore,We also assume thatwhere I is the identity operator.By Lemma 2.3,we haveFrom(2.2)and(3.3),we obtain
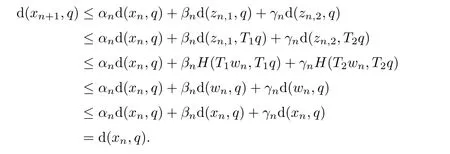


From(2.2),for any i=1,···,r,we have
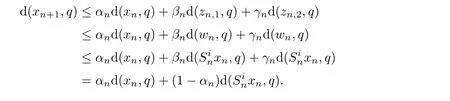
Therefore,

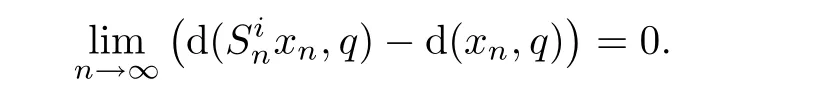
Using(2.2)and firmly nonexpansivity offor all i=1,2,···,r and n ∈ N,we obtain
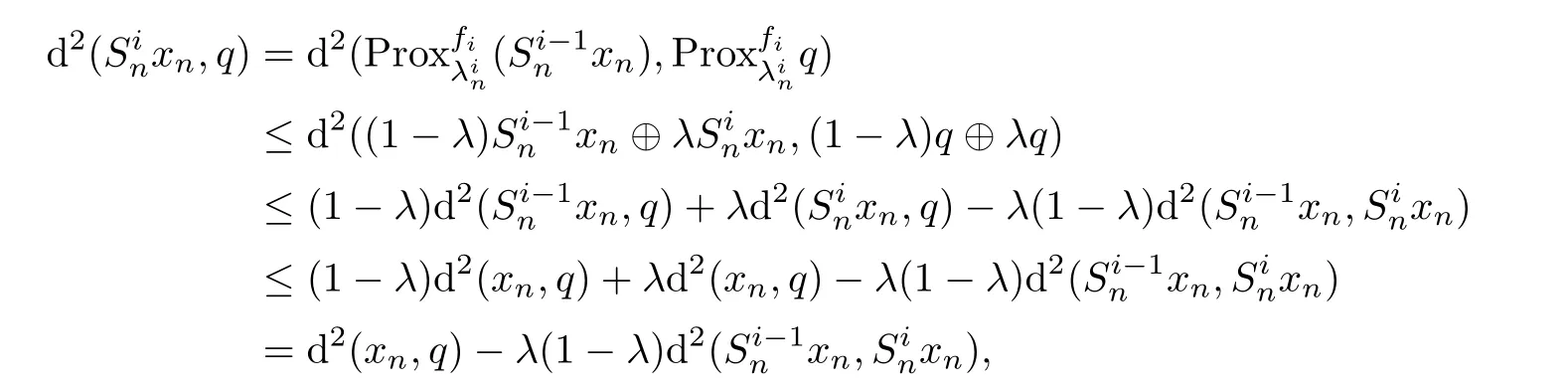
for all λ∈(0,1),which implies that
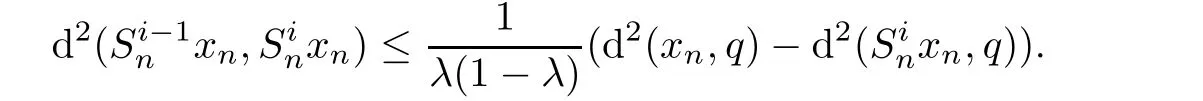
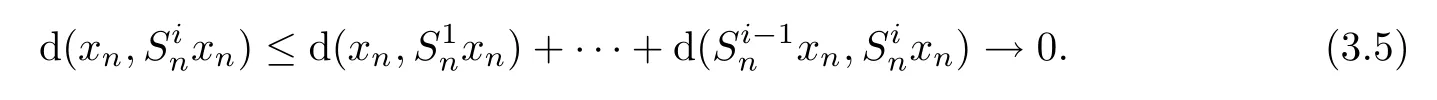
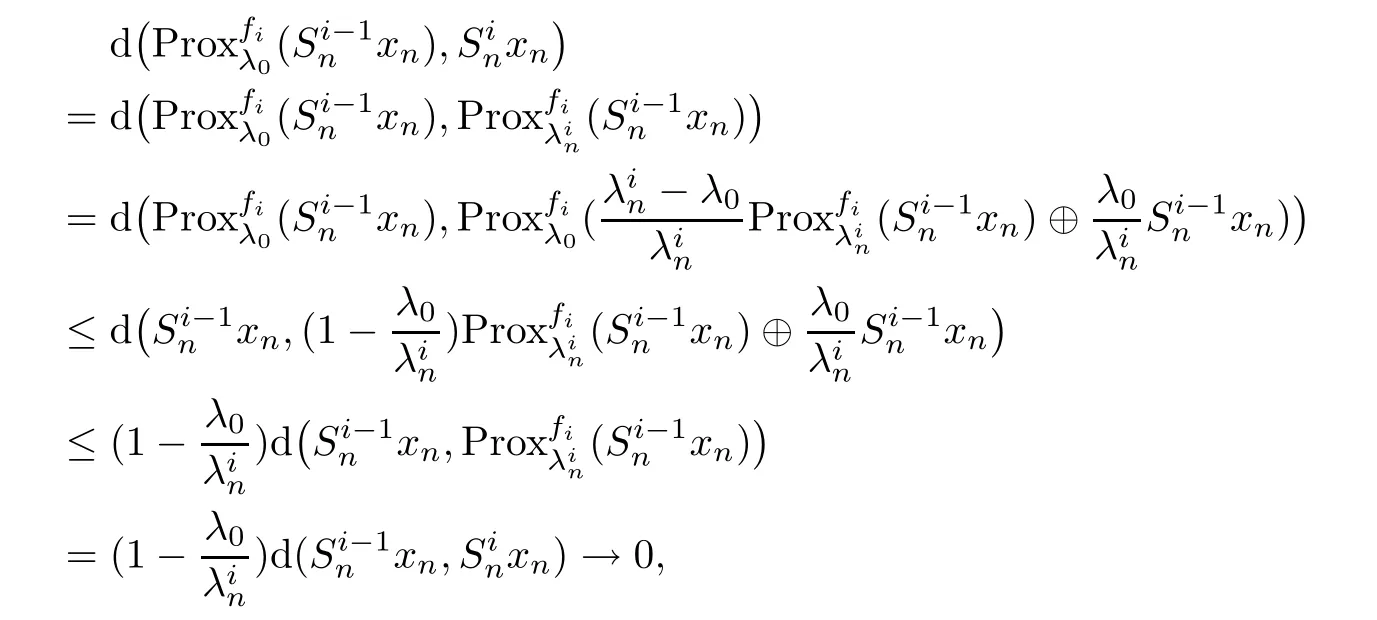
as n → ∞.So,for all i=1,2,···,r,we have

Therefore,
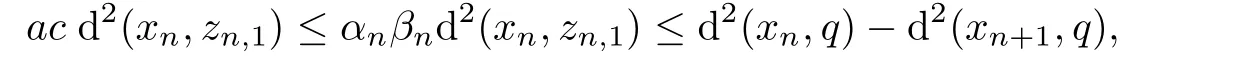
and hence

From(2.3),we obtain

Therefore,

From 0 Using(3.7)and(3.8),we get as n→0.This,together with(3.5)and(3.7),gives Let W∆(xn):= ∪A({un}),where the union is taken over all subsequences{un}of{xn}.We claim that W∆(xn)⊂ Ω.Let u∈W∆(xn),then there exists a subsequence{un}of{xn}such that A({un})={u}.By Lemmas 2.1 and 2.2,there exists a subsequence{unk}of{un}such thatLet{wnk}be the subsequence of{wn}corresponding to{unk},then,In fact,if not,there exists a subsequence{wnkm}of{wnk}such thatthen usingand the uniqueness of asymptotic center,we have Finally,we show that the sequence{xn} ∆-converges to a point in Ω.To this end,it suffices to show that W∆(xn)consists of exactly one point.Let{un}be a subsequence of{xn}with A({un})={u}and let A({xn})={x}.As{d(xn,u)}converges,by Lemma 2.3,we have x=u.Hence,W∆(xn)={x}.This completes the proof. ? As every Hilbert space is an Hadamard space,we obtain the following result. where zn,j∈Tj(wn),(j=1,2).Assume that the following conditions hold: (i) αn+βn+γn=1,αn∈ [a,b]⊂ (0,1),βn∈ [c,1)⊂ (0,1),γn∈ [d,e]⊂ (0,1),n ∈ N. Convex feasibility problemLet C be a nonempty closed convex subset of an Hadamard space X andbe a finite family of nonempty closed convex subsets of C such thatThe convex feasibility problem(CFP)is to find For a nonempty closed convex subset C of an Hadamard space(X,d),the indicator function is a proper convex and lower semi-continuous function andTherefore,letting fj=iCjfor j=1,2,···,r in Theorem 3.4,we get a ∆-convergence theorem for approximating a solution of a convex feasibility problem and a common fixed point of two multivalued hybrid mappings in Hadamard spaces.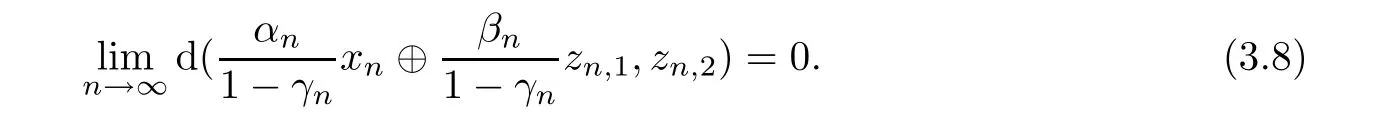
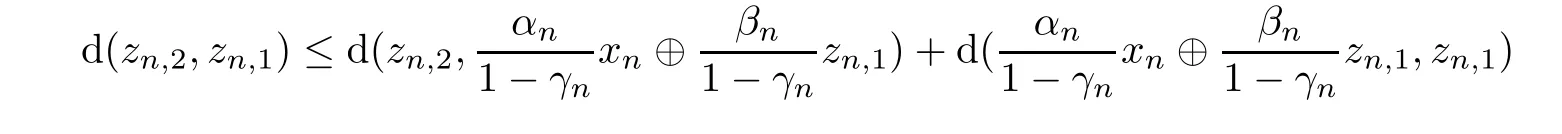




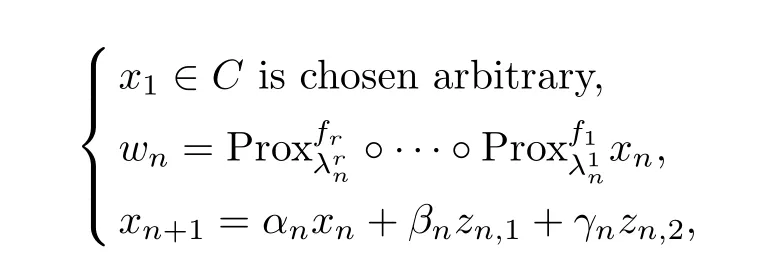

 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
- Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL EXISTENCE OF CLASSICAL SOLUTIONS TO THE HYPERBOLIC GEOMETRY FLOW WITH TIME-DEPENDENT DISSIPATION∗
- NONNEGATIVITY OF SOLUTIONS OF NONLINEAR FRACTIONAL DIFFERENTIAL-ALGEBRAIC EQUATIONS∗
- GROWTH AND DISTORTION THEOREMS FOR ALMOST STARLIKE MAPPINGS OFCOMPLEX ORDER λ∗
- EXACT SOLUTIONS FOR THE CAUCHY PROBLEM TO THE 3D SPHERICALLY SYMMETRIC INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
- CONVERGENCE FROM AN ELECTROMAGNETIC FLUID SYSTEM TO THE FULL COMPRESSIBLE MHD EQUATIONS∗
- ON ENTIRE SOLUTIONS OF SOME TYPE OF NONLINEAR DIFFERENCE EQUATIONS∗
