GLOBAL WEAK SOLUTIONS TO A GENERALIZED BENJAMIN-BONA-MAHONY-BURGERS EQUATION∗
Rui LI(李睿) Chong LAI(赖翀)Yonghong WU(吴永洪)
Department of Mathematics and Statistics,Curtin University,Perth,Australia
E-mail:rui.li14@postgrad.curtin.edu.au;laichong1991716@gmail.com;y.wu@curtin.edu.au
Abstract The existence of global weak solutions for a generalized Benjamin-Bona-Mahony-Burgers equation is established in the spaceunder the condition that its initial value belongs to the space H1(R).A one-sided super bound estimate and a space-time higher-norm estimate on the first order derivatives of the solution with respect to the space variable are derived to prove the existence.
Key words Generalized Benjamin-Bona-Mahony-Burgers equation;global weak solution;weak limits
1 Introduction
In this work,we investigate the Cauchy problem for the following generalized Benjamin-Bona-Mahony-Burgers equation

where a≥0,b and k are constants,and p≥1 is an integer.When k=0,equation(1.1)is the nonlinear Benjamin-Bona-Mahony-Burgers equation(BBMB).Setting a=0,b=1,p=1,and k=0,equation(1.1)becomes the Benjamin-Bona-Mahony model(see[1,2]).
There are lots of works to study the Benjamin-Bona-Mahony-Burgers equation and its various generalizations.Chen and Wang[3]give a stability criteria for the solitary wave solutions of the Benjamin-Bona-Mahony-Burgers equation which contains coupled nonlinear terms.The nonlinear stability of nonlinear periodic solutions of the regularized Benjamin-one equation and the BBM equation associated with perturbations of the wavelength is established in[1].Using the L-function method,Feng et al[4]obtained the asymptotic behavior of solutions for the time-delayed equations of Benjamin-Bona-Mahony’s type.The tanh technique with the aid of symbolic computational system is employed to find exact solutions of BBMB-type equations[5].The periodic initial value problem which contains the generalized Benjamin-Bona-Mahony equation with generalized damping on the one-dimensional torus is considered in[6].The homogeneous balance method and symbolic computations are employed in[7]to find out many new exact traveling wave solutions for the Benjamin-Bona-Mahoney equation.The long time existence result for the Cauchy problem related to the BBM-Boussinesq systems was studied in[8].For the existence of global weak solutions of the relating partial differential equations,the reader is referred to[9–13]and the references therein.
The existence of global weak solutions and strong solutions for equation(1.1)with k=0 has been investigated by many scholars(see[1–5]).The objective of this work is to establish the existence of global weak solutions for the generalized Benjamin-Bona-Mahoney-burgers equation(1.1)with the term kuxxxunder the assumption that its initial value belongs to the space H1(R).
The approaches used in this work come from those presented in[13](also see[14]).Namely,it needs us to show that the derivativewhich is only weakly compact,converges strongly.The key factor to prove that weak convergence is equal to strong convergence is the higher integrability estimate(3.17)in Section 3.This derives that the weak limit ofdoes not contain singular measures.
The organization of this article is structured as follows.Section 2 gives the main result and Section 3 presents the viscous problem and a corresponding well-posedness result.An upper bound,a higher integrability estimate,and some basic compactness properties for the viscous approximations are also built up in Section 3.Strong compactness of the derivative of solutions for the viscous approximation problem is obtained in Section 4 in which the main result is proved.
2 Main Result
We write the Cauchy problem for equation(1.1)in the form
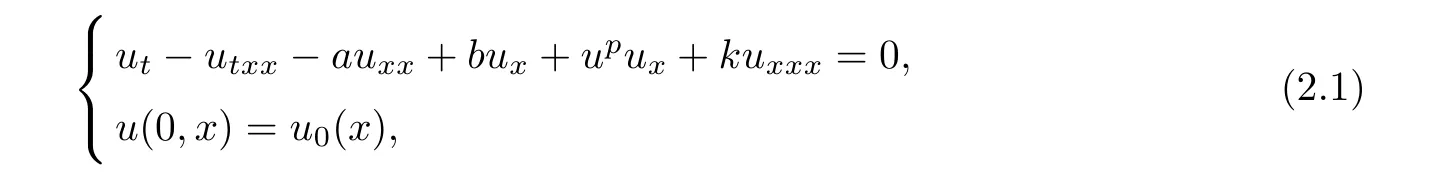
which is equivalent to

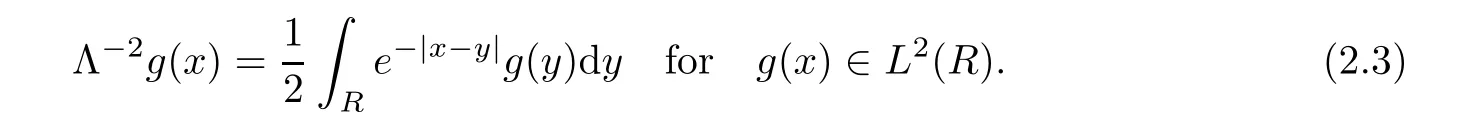
Using integration by parts,we derive that

where u0=u(0,x)andUsing(2.4)and a≥ 0 yields

where c is a positive constant.
We introduce the definition of global weak solutions to problem(2.1)or(2.2)(see[13]).
Definition 2.1A function u:[0,∞)×R→R is said to be a global weak solution to the Cauchy problem(2.2)if
(iii) u=u(t,x)satisfies(2.2)in the sense of distributions and takes on the initial value pointwise.
Now we state the main result.
Theorem 2.2If u0(x)∈H1(R),then problem(2.1)or(2.2)has a global weak solution u(t,x)in the sense of Definition 2.1.Moreover,the weak solution satisfies the properties.
(a)There exists a positive constant c0depending on k u0kH1(R)and the coefficients of equation(1.1)to satisfy the following one-sided L∞norm estimate on the first order spatial derivative
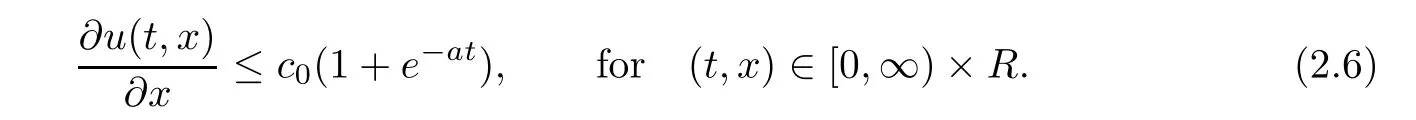
(b)For any T∈(0,∞),there exists a positive constant c1depending only on k u0kH1(R)and the coefficients of equation(1.1)to satisfy the space higher integrability estimate

3 Viscous Approximations
Setting


To establish the existence of global weak solution to Cauchy problem(2.2),we consider the viscous approximation problem

We will prove the compactness of a sequence of smooth functions{uε}.Throughout this work,let c denote any positive Constant which is independent of parameter ε.
We start our analysis by giving the following well-posedness result for problem(3.3).
Lemma 3.1Let u0∈ H1(R).Then,there exists a unique solution uε∈ C([0,∞);Hσ(R))(σ ≥ 2)to the Cauchy problem(3.3)with uεsatisfying or


ProofFor any σ ≥ 2 and u0∈ H1(R),we know uε,0∈ C([0,∞);Hσ(R)).Applying Theorem 2.3 in[15],we derive that problem(3.3)has a unique solution
Consider the equivalent form of the first equation of problem(3.3)

Multiplying(3.6)by uεand integrating by parts give rise to
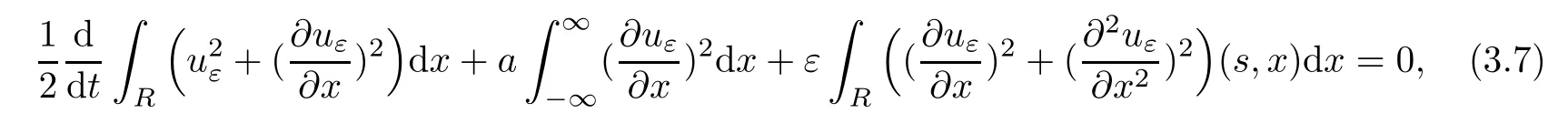
which completes the proof.
Using Lemma 3.1 yields
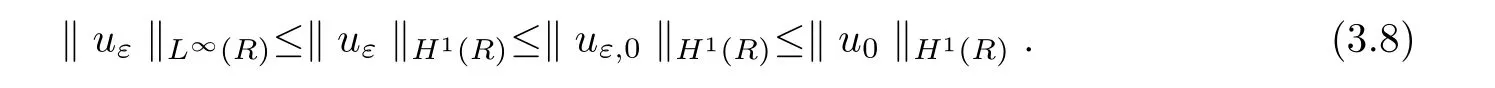
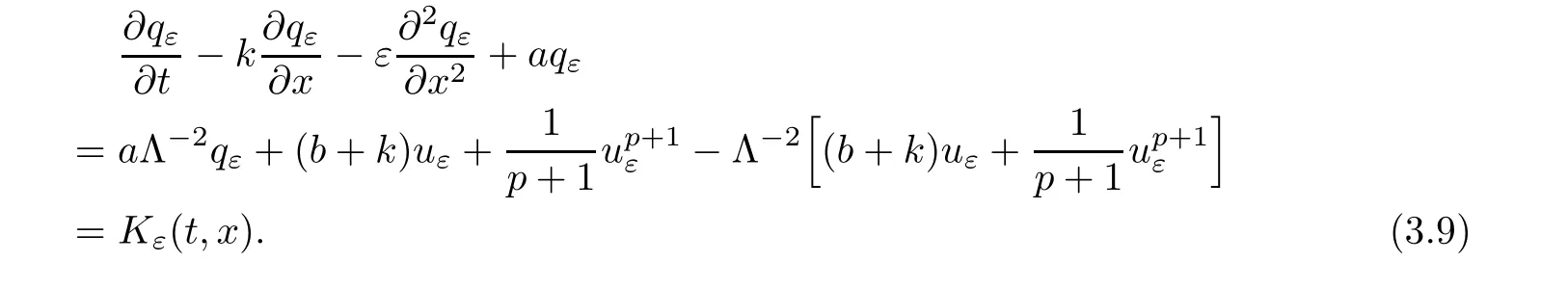
Lemma 3.2There exists a positive constant c depending only on k u0kH1(R)and the coefficients of equation(1.1)such that

where uε=uε(t,x)is the solution of system(3.3).
ProofWe have

and

Using(3.8),(3.13),and(3.14),we know that(3.10)is valid.
Because

and

from(3.15)–(3.16),we derive that(3.11)holds.
Proceeding as for the proof of(3.13)–(3.16),it is obtained that(3.12)holds.The proof of Lemma 3.2 is completed. ?
Lemma 3.3Let t∈[0,T].There exists a positive constant c1depending only onand the coefficients of equation(1.1),but independent of ε,to satisfy the space higher integrability estimate

where uε=uε(t,x)is the solution of problem(3.3).
ProofMultiplying(3.9)by,we have

Note that

and
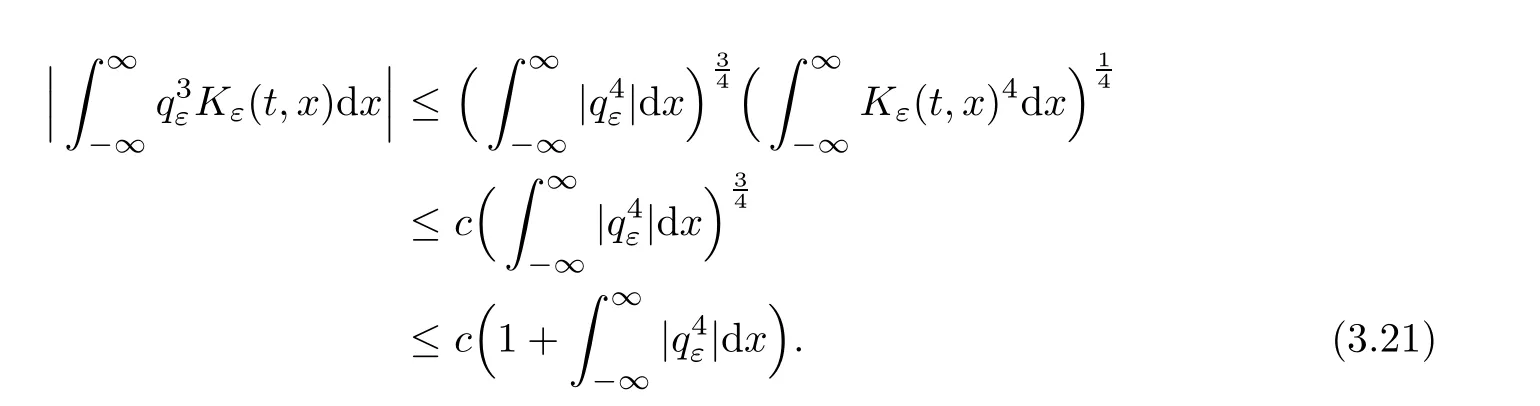
From(3.18)–(3.21),we get

which derives that(3.17)holds.?
Lemma 3.4Let uε=uε(t,x)be the unique solution of(3.3).There exists a positive constant c depending only onand the coefficients of equation(1.1)to satisfy the following one-sided L∞norm estimate on the first order spatial derivative

ProofFrom(3.9)and Lemma 3.2,we know that there exists a positive constant c depending only on k u0kH1(R)and the coefficients of equation(1.1)such thatTherefore,

Let g=g(t)be the solution of


Lemma 3.5There exists a sequence{εj}j∈Ntending to zero and a function K ∈L∞([0,∞)×R)such that

where
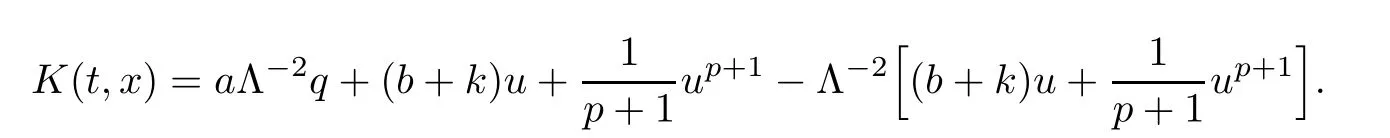
ProofFor 0 We will prove that In fact,we have and Using Lemma 3.2 gives rise to Similarly,we have Because each term of Kε(t,x)has the same property as the Kε(t,x)does,applying Corollary 4 at page 85 in[16],we can choose a subsequence of εj→ 0,still denoted by εj,such that which completes the proof. Lemma 3.6There has a sequence{εj}j∈Ntending to zero and a functionT such that The proof of Lemma 3.6 is fully similar to that of Lemma 5.2 in[14].Here,we omit its proof. In the following of this article,we apply overbars to represent weak limits(the space in which these weak limits are taken iswith 1 Lemma 3.7There has a sequencetending to zero and two functions q ∈such that and ProofLimitations(3.36)and(3.37)are direct consequence of Lemmas 3.1 and 3.3.Inequality(3.38)is valid because of the weak convergence in(3.34).Finally,(3.39)is a consequence of the definition of qε,Lemma 3.6,and(3.36). ? For any convex function φ ∈ C1(R)with φ′being bounded and Lipschitz continuous on R,applying(3.36),we get Multiplying equation(3.24)by φ′(qε)yields Lemma 3.8For any convex φ ∈ C1(R)with φ′being bounded and Lipschitz continuous on R, in the sense of distributions on[0,∞) × R.Here,qφ′(q)is the weak limits ofin ProofIn(3.42),using the convexity of φ,Lemmas 3.5,3.6 and 3.7,sending ε → 0,we completes the proof. ? From(3.36)and(3.37),we know that almost everywhere in[0,∞)× R,wherefor η ∈ R.From Lemma 3.4 and(3.36),we have Lemma 3.9In the sense of distributions on[0,∞)× R,it holds that ProofUsing(3.9),Lemmas 3.5,3.6 and 3.7,conclusion(3.46)holds by taking limit for ε→0 in(3.9). ? The following lemma is a generalized formulation of(3.46). Lemma 3.10For any φ ∈ C1(R)with φ ∈ L∞(R),it holds that in the sense of distributions on[0,∞)× R. ProofAssume that{ψδ}δis a family of mollifiers defined on R.Denote qδ(t,x):=(q(t,.)⋆ ψδ)(x),where ⋆ is the convolution with respect to x.Multiplying(3.46)by φ′(qδ),we have Using the boundedness of φ,φ′and letting δ→ 0 in the above equation,we know that(3.47)holds. In this section,we shall show that the weak convergence of qεin(3.37)is strong convergence,and then establish the global existence result of our main results.As the measurewe will prove that if the measure is zero initially,then it will continue to be zero at later time t>0. Lemma 4.1([13,14]) Assume u0∈H1(R).It holds that Lemma 4.2([13,14]) If u0∈H1(R),for each M>0,it holds that where Lemma 4.3([13,14]) Let M>0.Then,for each η ∈R,it holds that Lemma 4.4Assume u0∈H1(R).Then,for almost all t>0,it holds that ProofFor an arbitrary T>0(0 Lemma 4.5For any t>0 and M>0,it holds that ProofLet M>0.Subtracting(3.43)from(3.47)and using entropywe deduce Integrating inequality(4.10),we complete the proof. ? Lemma 4.6It holds that ProofApplying Lemmas 4.4 and 4.5 gives rise to It follows from Lemma 4.3 that From Lemma 3.5,we know that there exists a constant C>0,depending only on k u0kH1(R),such that Using(3.44)and Lemma 4.3 derives Thus,by the convexity of the map,we get Then,from(4.12),(4.13),and(4.16),we have which completes the proof.? ProofUsing(3.2),(3.5),and Lemma 3.5,we know that conditions(i)and(ii)in Definition 2.1 hold.We have to verify(iii).Applying Lemma 4.6,we have Letting M→∞,we obtain From Lemma 3.6,(3.27),and(4.19),we know that u is a distributional solution to problem(2.2).In addition,inequalities(2.6)and(2.7)are deduced from Lemmas 3.3 and 3.4.Therefore,we complete the proof of Theorem 2.2. ?

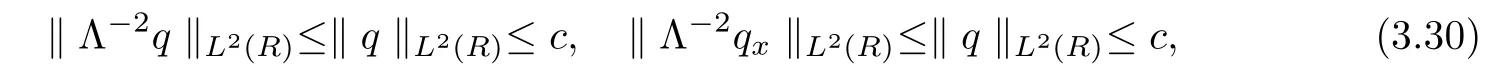







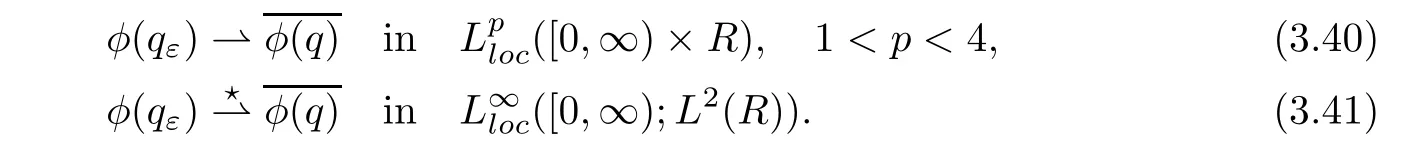
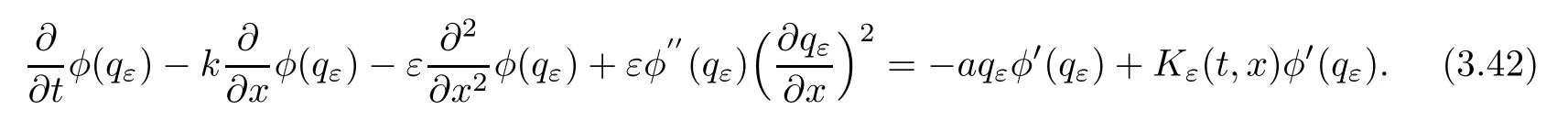
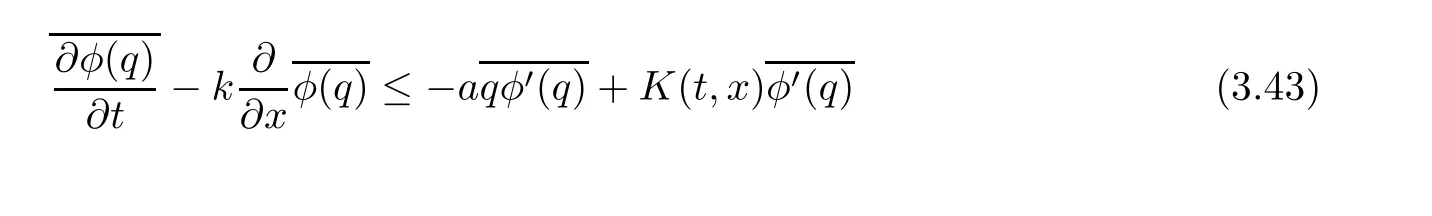

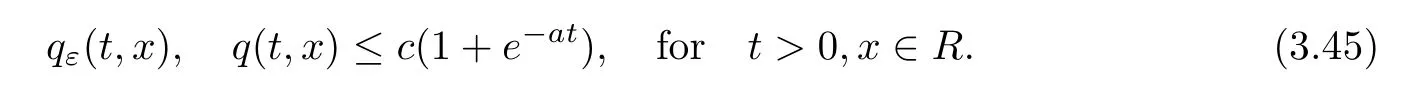



4 Strong Convergence of qεand Proof of Main Results

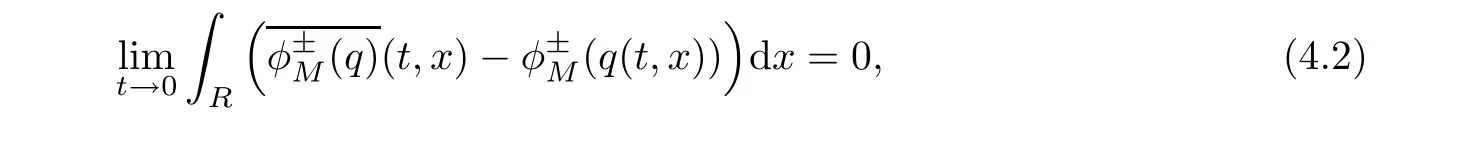

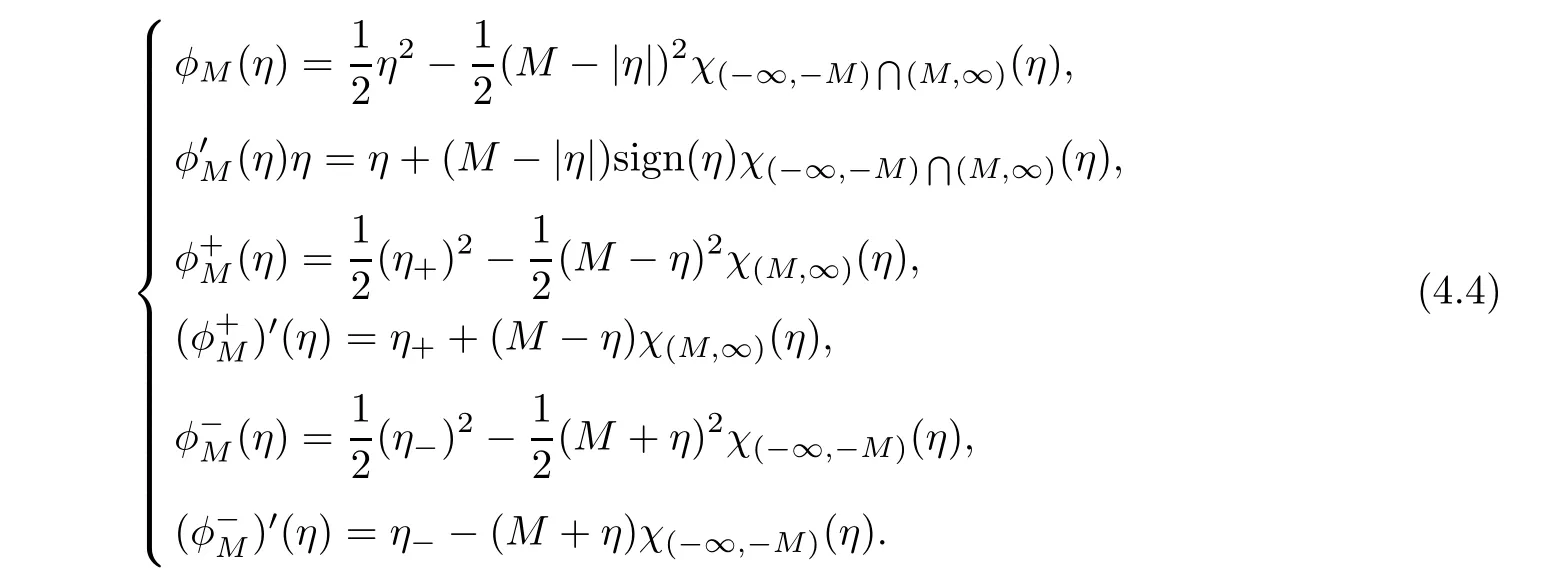

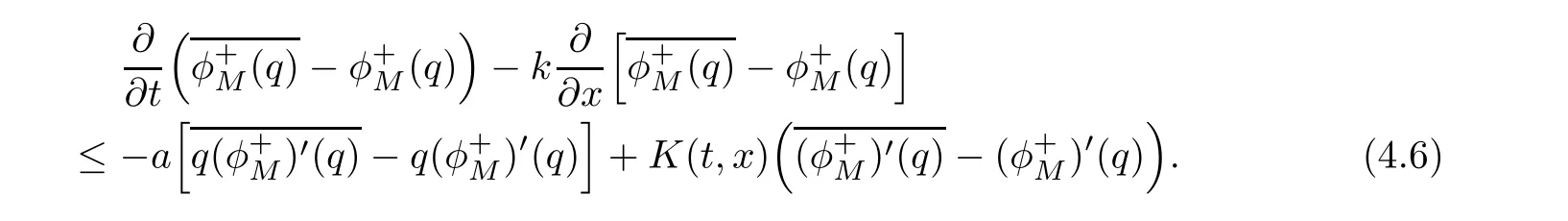


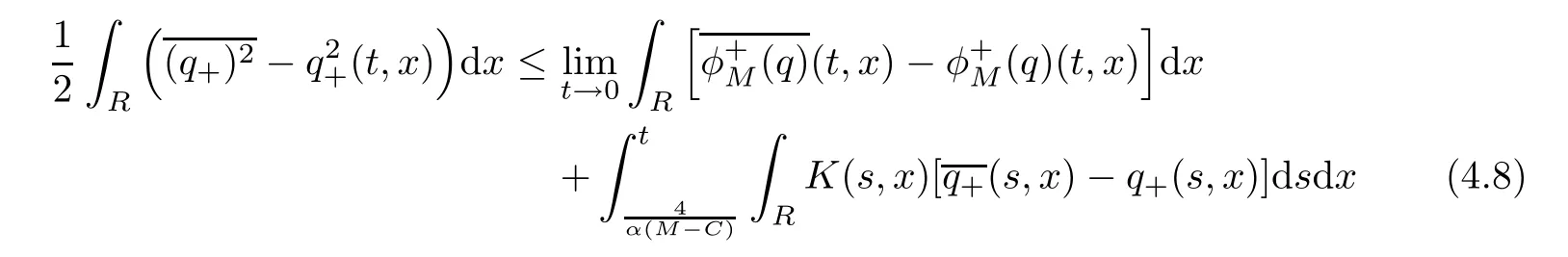


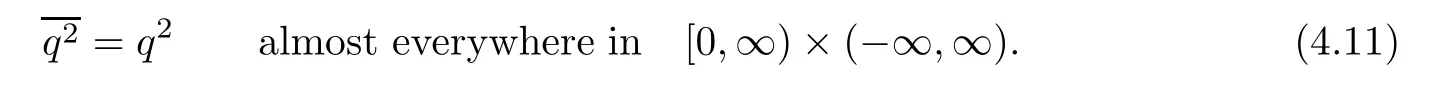

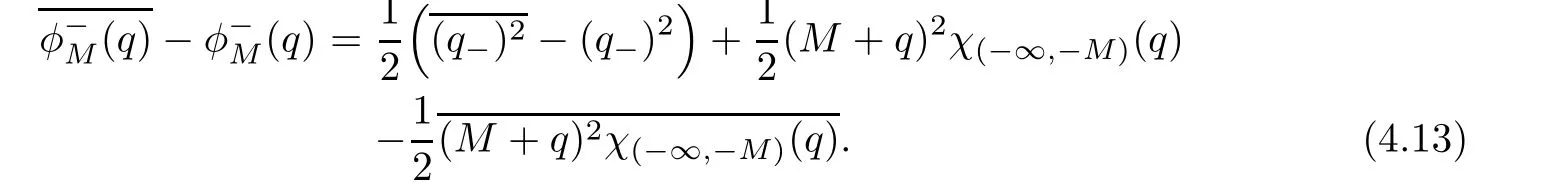

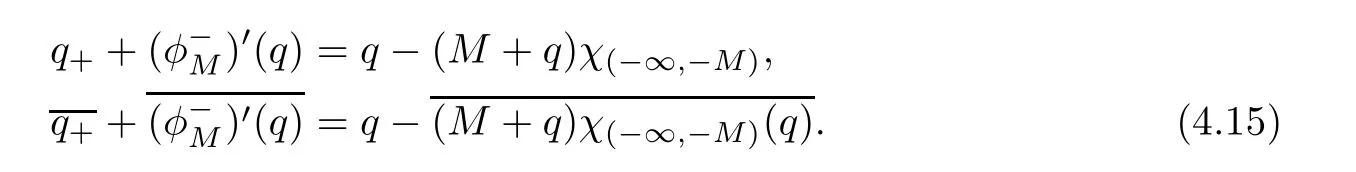


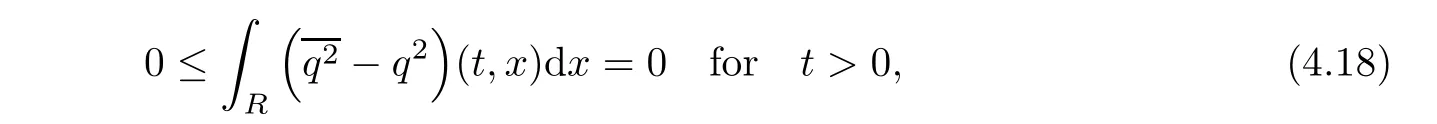

 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
