BLOW-UP PROBLEMS FOR NONLINEAR PARABOLIC EQUATIONS ON LOCALLY FINITE GRAPHS∗
Yong LIN(林勇)Yiting WU(吴艺婷)
Department of Mathematics,Renmin University of China,Beijing 100872,China
E-mail:linyong01@ruc.edu.cn;yitingly@126.com
Abstract Let G=(V,E)be a locally finite connected weighted graph,and∆be the usual graph Laplacian.In this article,we study blow-up problems for the nonlinear parabolic equation ut=∆u+f(u)on G.The blow-up phenomenons for ut=∆u+f(u)are discussed in terms of two cases:(i)an initial condition is given;(ii)a Dirichlet boundary condition is given.We prove that if f satisfies appropriate conditions,then the corresponding solutions will blow up in a finite time.
Key words Blow-up;parabolic equations;locally finite graphs;differential inequalities
1 Introduction and Main Results
As is known to us,many structures in our real life can be represented by a connected graph whose vertices represent nodes,and whose edges represent their links,such as the internet,brain,organizations,and so on.In recent years,the investigations of discrete weighted Laplacians and various equations on graphs have attracted attention from many authors(see[1,4,5,9–12,15,16,18,20]and references therein).There have been some works on dealing with blowup phenomenons of equations on graphs;for example,Xin et al[20]investigated the blow-up properties of the Dirichlet boundary value problem for ut=∆u+up(p>0)on a finite graph.However,as far as we know,the blow-up phenomenon on a locally finite graph has not been studied in the literature.The main concern of this article is to discuss blow-up phenomenons for the nonlinear parabolic equation ut=∆u+f(u)on a locally finite graph.This equation is the mathematical model of heat diffusion and can be used to model solid fuel ignition[2].The function f(u)is typically a nonlinear function,such as up(p>1).The main purpose of this article is to study blow-up phenomenons for the nonlinear parabolic equation in terms of the following two cases:(i)an initial condition is given;(ii)a Dirichlet boundary condition is given.
Let G=(V,E)be a locally finite connected graph,where V denotes the vertex set of G and E denotes the edge set of G.For any T>0,a function u=u(t,x)is said to be a solution of(1.1)(or(1.2))in[0,T]×V,if equation(1.1)(or(1.2))is satisfied by u in[0,T]×V,meanwhile,u is bounded and continuous with respect to t in[0,T]×V.A solution u of(1.1)(or(1.2))in[0,+∞)×V is a function whose restriction to[0,T]×V is a solution of(1.1)(or(1.2))in[0,T]×V for any T>0.Moreover,we say that a solution u blows up in a finite time T,if there exists x∈V such that

Focussing on the research goals mentioned above,in this article,we first deal with the blow-up phenomenon of the following Cauchy problem on G
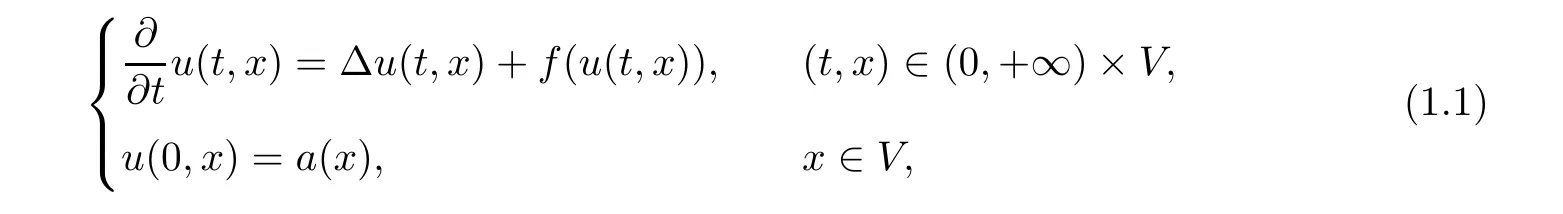
where∆ isµ-Laplacian on G.
Given a non-empty finite subset Ω ⊂ V,the boundary of Ω is defined by
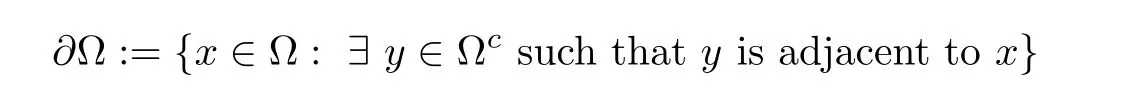
and the interior of Ω is defined by Ω◦:= Ω∂Ω.In this article,we assume that Ω◦is non-empty.
Next,we consider the blow-up phenomenon arising from the following discrete nonlinear parabolic equations on G
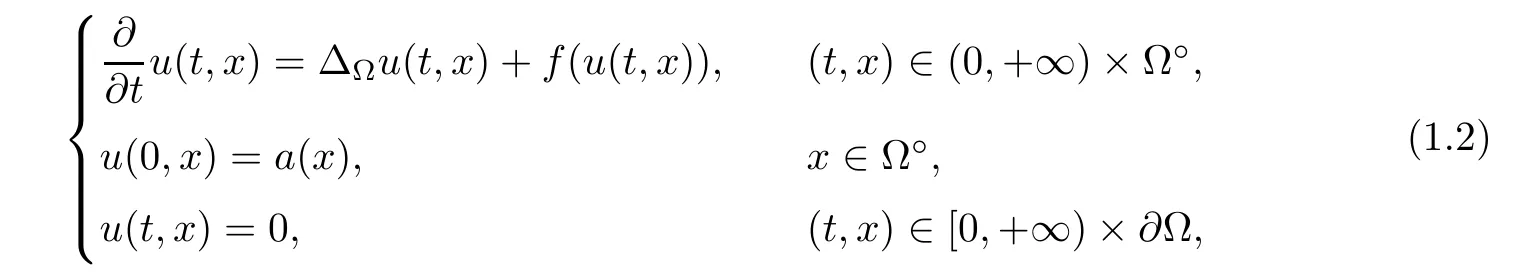
where ∆Ωis Dirichlet Laplacian on Ω◦.
The earlier blow-up results on parabolic equations on R are due to Kaplan[13]and Fujita[6,7].For the finite time blow-up,Osgood[17]gave a criterion,namely,the nonlinear term on the right-hand side of equation ut=∆u+f(u)must satisfy

In this article,we consider blow-up problems for the nonlinear parabolic equation ut=∆u+f(u)on a locally finite graph G.We establish our results under assumptions that f satisfies the following properties:
(H1)f is continuous in[0,+∞);
(H2)f(0)=0 and f(τ)>0 for all τ>0;
(H3)f is convex in[0,+∞);
Our main results are stated in Theorems 1.1 and 1.2 below.
Theorem 1.1Let G be a locally finite connected graph and have polynomial volume growth of degree m>0.Suppose that f satisfies the assumptions(H1)–(H4);a(x)given by(1.1)is bounded,non-negative,and not trivial in V.Set

If there exists a real number θ∈(0,1)such that

for sufficiently large t,then the non-negative solution u of(1.1)blows up in a finite time.

is the smallest eigenvalue of−∆Ω,and φ1(x)is the eigenfunction corresponding to λ1(Ω).
Remark 1.3In particular,if we choose f(u)=u1+α(α >0)in Theorem 1.1,then

Theorem 1.1 shows that the solution of(1.1)blows up if the following condition(c1)is satisfied.
(c1).There exists a real number θ∈(0,1)such that for sufficiently large t,
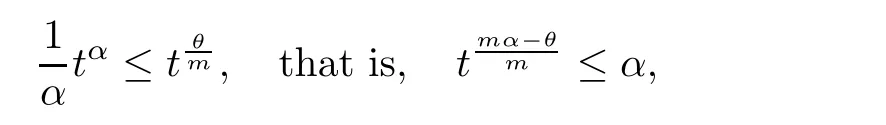
where m and α are positive constants.
It is easy to find that for sufficiently large t and positive constants m,α,θ,we have
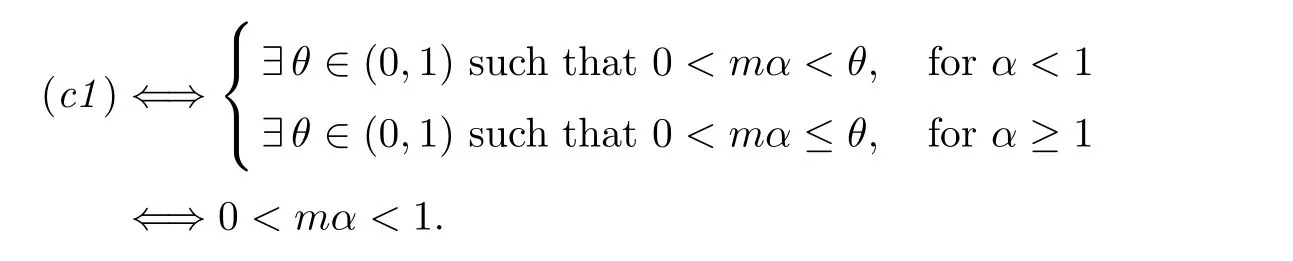
The assertion in Remark 1.3 leads to the following result,which was obtained by Lin and Wu in an earlier article[15].
Corollary 1.4Let G be a locally finite connected graph and have polynomial volume growth of degree m>0.If 0 blows up for any bounded,non-negative,and non-trivial initial value,where α>0. Remark 1.5Let f(u)=u1+α(α >0),then Theorem 1.2 shows that the solution of(1.2)blows up if The remaining parts of this article are organized as follows.In Section 2,we introduce some concepts,notations,and known results which are essential to prove the main results of this article.In Sections 3 and 4,we give the proofs of Theorems 1.1 and 1.2,respectively. Let G=(V,E)denote a locally finite connected graph.In this article,we consider weighted graphs,that is,we allow the edges and vertices on G to be weighted.Let ω:V ×V →[0,∞)be an edge weight function satisfying ωxy= ωyxfor all x,y ∈ V and ωxy>0 if and only if x is adjacent to y(also denoted by).Furthermore,letµ:V →(0,∞)be a positive weight function on vertices of G and satisfy µ0:=infx∈Vµ(x)>0.In particular,all the graphs in our concern are assumed to satisfy A function on a graph is understood as a function defined on its vertex set.We use the notation C(V)to denote the set of real functions on V.For any 1≤p<∞,we denote by the set of ℓpintegrable functions on V with respect to µ.For p= ∞,let The integral of a function h ∈ ℓ1(V,µ)is defined by For any function h∈C(V),theµ-Laplacian∆of h is defined by It can be checked that Dµ< ∞ is equivalent to theµ-Laplacian ∆ being bounded on ℓp(V,µ)for all p∈[1,∞](see[12]). Given a finite subset Ω ⊂ V,we denote by C(Ω◦)the set of real functions on Ω◦.For any function h ∈ C(Ω◦),the Dirichlet Laplacian ∆Ωon Ω◦is defined as follows:First we extend h to the whole V by setting h ≡ 0 outside Ω◦and then set Thus,for any x∈Ω◦,we have We say that a function p:(0,+∞)×V×V→R is a fundamental solution of the heat equation ut=∆u on G,if for any bounded initial condition u0:V→R,the function is differentiable in t,satisfies the heat equation,and for anyholds. For completeness,we recall some important properties of the heat kernel p(t,x,y)on G as follows: Proposition 2.1(see[18,19]) For t,s>0 and any x,y∈V,we have (i)p(t,x,y)=p(t,y,x), (ii)p(t,x,y)>0, Lin et al[14]utilized polynomial volume growth condition to obtain an on-diagonal lower estimate of heat kernels on graphs for large time.We recall it bellow. Proposition 2.2(see[14]) Assume that G satisfies polynomial volume growth,then for large enough t, As a preparation for the proof of Theorem 1.1,we first introduce two lemmas. Lemma 3.1Let G be a locally finite connected graph.For any T>0,if g is bounded in V,then for anyconverges uniformly in(0,T]. ProofWe begin with recalling a previous result which was obtained in[18].If∆is a bounded operator,then we have Because g is bounded in V,we can assume that|g(x)|≤A in V,then By iteration,we obtain,for any k∈N and x∈V, Thus,for any t∈(0,T]and x∈V, In view of This completes the proof of Lemma 3.1. Lemma 3.2Let G be a locally finite connected graph.For any t>0 and x∈V,if g is bounded in V,then we have ProofAs before,because g is bounded in V,we assume that|g(x)|≤A in V. A direct computation yields Note that the above summations can be exchanged,on account of Thus,Lemma 3.2 is proved. Proof of Theorem 1.1Suppose that there exists a non-negative solution u=u(t,x)of(1.1)in[0,+∞)×V.Because a(x)is non-negative and not trivial in V,we can assume that a(ν)>0 with ν ∈ V. Taking an arbitrary T>0,we put Obviously,JTis continuous with respect to s.Because u is bounded,according to Lemma 3.1,we know that JTexists even though G is locally finite. Firstly,we show that JTis positive for all s∈[0,T). Because u(s,ν)is non-negative in[0,T)and f is non-negative in[0,+∞),it follows that for all 0≤s Note that then inequality(3.4)gives which,together with a(ν)=u(0,ν)>0,yields Hence,for all 0≤s In view of the fact that p(T − s,ν,x)is positive,then JT(s)is positive in[0,T). Secondly,we shall prove that JTis differentiable with respect to s and satisfies the following equation Because u is bounded,by Lemma 3.1,we know that JTis uniformly convergent.Note also that,f is continuous in[0,+∞),which and the boundedness of u imply that f(u)is bounded.Utilizing the above arguments and Lemma 3.1,thenis also uniformly convergent.Hence,we can exchange the order of summation and derivation,and then we get From the property of heat kernel and Lemmas 3.1 and 3.2,we have Thirdly,we need to show that In view of f(0)=0,we have We have shown that JTandboth are convergent,which together with(3.7)and yields This is the desired inequality(3.6). Next,we consider the following function: It is not difficult to find that this function is well-defined,because JT(s)>0 for any s∈[0,T)and f(τ)>0 for all τ>0. We observe from(3.6)that for any s∈[0,T), Owing to Q(0)=0 and using the Mean-value theorem,for any 0<ε Because f(τ)>0 for all τ>0 and JT(s)>0 for any s ∈ [0,T),we conclude that F(JT(s))is positive for all s∈[0,T).Hence,we deduce from inequality(3.8)that Letting ε→ 0,we obtain From the given condition V(x,r)≤c0rm(c0>0,r≥0,m>0)and Proposition 2.2,we have,for large enough T, Hence,for sufficiently large T,we have Letting us come back to inequality(3.9),then together with(3.11)and the fact that F is non-increasing,one obtains for large enough T. In contrast,it is easy to observe from the limit that for sufficiently large T.So,we can choose a real number T1>0 such that for all T>T1.By f(τ)>0 for τ>0,we find that F is strictly decreasing in(0,+∞).Thus,we have for all T>T1. The given condition(1.3)in Theorem 1.1 shows that there exist real numbers T2∈(0,+∞)and θ∈(0,1)such that for T>T2, Combining(3.13)and(3.14),we obtain for all T>max{T1,T2}.However,this contradicts with(3.12). The proof of Theorem 1.1 is completed. To prove Theorem 1.2,we need the following two lemmas. Lemma 4.1(Strong maximum principle) Let G=(V,E)be a locally finite connected graph and Ω⊂V be finite.For any T>0,we assume that v(t,x)is bounded and continuous with respect to t in[0,T]×Ω,which satisfies where k(t,x)is bounded in(0,T]×Ω◦.Then,v(t,x)≥ 0 in[0,T]×Ω. ProofSetThen,we have Lv≥ 0 in(0,T]×Ω◦.Because k(t,x)is bounded in(0,T]×Ω◦,we can assume that there exists a positive number l such that l>k(t,x)for all(t,x)∈ (0,T]×Ω◦.Using a transformation ψ =ve−lt,we get It is easy to observe that for any(t,x)∈ [0,T]×Ω◦. Because v(t,x)is bounded and continuous with respect to t,we conclude that ψ(t,x)is also bounded and continuous with respect to t in[0,T]× Ω◦,which implies that ψ(t,x)exists a minimum value in[0,T]×Ω◦. Let(t0,x0)be a minimum point of function ψ in[0,T]× Ω◦.To prove v(t,x) ≥ 0 in[0,T]×Ω◦,we need to verify that ψ(t,x)≥ 0 in[0,T]×Ω◦;it is sufficient to prove ψ(t0,x0)≥ 0. In the following,we will prove ψ(t0,x0)≥ 0 by contradiction.Assume that ψ(t0,x0)<0. Case 1If t0=0,then it follows from(4.1)that ψ(0,x0)=v(0,x0)≥ 0.This contradicts with ψ(t0,x0)<0. Case 2If t0∈ (0,T],then we deduce from k(t0,x0) (if t0 On the other hand,the functionin Ω◦attains the minimum at x=x0,thus, Applying(4.4)to(4.3),we obtainwhich is a contradiction within(0,T]×Ω◦. Hence,we have ψ(t0,x0)≥ 0,which leads to ψ(t,x)≥ 0 in[0,T]× Ω◦. In view of we deduce that v(t,x)≥ 0 in[0,T]×Ω◦. In addition,from(4.1)we have v(t,x)≥ 0 in[0,T]×∂Ω.Thus,we conclude that v(t,x)≥ 0 in[0,T]×Ω. The proof of Lemma 4.1 is completed.? Lemma 4.2(Comparison principle) Let G=(V,E)be a locally finite connected graph and Ω⊂V be finite.For any T>0,we assume that u(t,x)andare bounded and continuous with respect to t in[0,T]×Ω,which satisfy where g∈C1(R).Then,in[0,T]×Ω. ProofSetThen, Define a function Then, Next,we shall show that k(t,x)is bounded in(0,T]×Ω◦. Because u(t,x)and u(t,x)are bounded in[0,T]× Ω,there exists a constant M>0 such that for any(t,x)∈ [0,T]×Ω, Using the Mean-value theorem,we have In view of g∈C1(R),we deduce from the above inequality that k(t,x)is bounded in[0,T]×Ω,which implies that k(t,x)is bounded in(0,T]×Ω◦. Hence,it follows from Lemma 4.1 that Thus,Lemma 4.2 is proved. Proof of Theorem 1.2Suppose that there exists a solution u=u(t,x)of(1.2)in[0,+∞)×V. We consider the function where φ1is a eigenfunction corresponding to the smallest eigenvalue λ1(Ω)(see Section 2).It is clear that J(0)≡κ and J(t)is continuous with respect to t. Firstly,we show that J(t)is positive for all t∈[0,+∞). For an arbitrary(t,x)∈ [0,+∞)×Ω,there exists a positive number T such that(t,x)∈[0,T]× Ω.Consider the special case of Lemma 4.2 whenand g=f,and then the conditions(4.6)stated in Lemma 4.2 become By comparing equations(1.2)provided by Theorem 1.2 with(4.8)above,we deduce from Lemma 4.2 that u(t,x)≥ 0 in[0,T]×Ω,which implies that u(t,x)≥ 0 for all(t,x)∈ [0,+∞)×Ω in view of the arbitrariness of(t,x)∈[0,+∞)×Ω. Set Ω1:={x ∈ Ω◦:a(x)>0}.Because a(x)is not trivial in Ω◦,we getFor any z∈Ω1,because of the fact that f is non-negative in[0,+∞),we have A simple calculation shows that Combining(4.9)and(4.10),we verify that which implies that Hence,for any t≥0,we have Because µ(x)and φ1(x)are positive in Ω◦,we conclude that J(t)>0 for all t∈ [0,+∞).Secondly,we prove that By using the fact that∆Ωis self-adjoint,we have Combining(4.11)with(4.12)gives Thirdly,we will claim that there exists a positive constant K> κ such that f(τ)>2λ1τ for any τ≥K. We prove this assertion by contradiction.Assume that for any K> κ,there exists a τ∗≥ K such that On the basis of the assumption above,given a fixed K0>κ,there exists asuch that Because f(τ)is convex in[0,+∞),for anywe have Note that K is an arbitrary number that is greater thanwe obtain,for all Now,we are in a position to prove the assertion of Theorem 1.2. We observe that f(τ)and f(τ)− λ1τ are positive in[κ,+∞),thus, This yields It is clear that there is no singularity in the above integral,because J(0) ≡ κ >0 and f(τ),f(τ)− λ1τ are positive in[κ,+∞). On the other hand,it follows from(4.13)that This completes the proof of Theorem 1.2.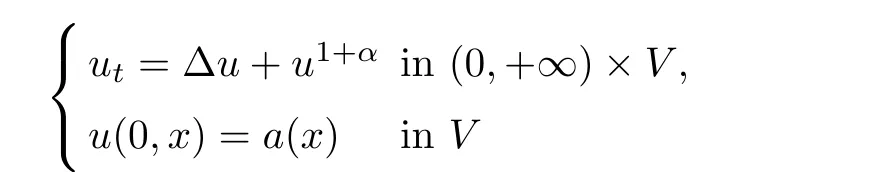
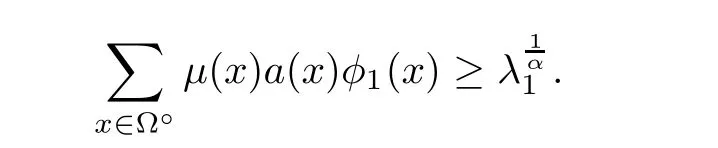
2 Preliminaries

2.1 The Laplacian on graphs
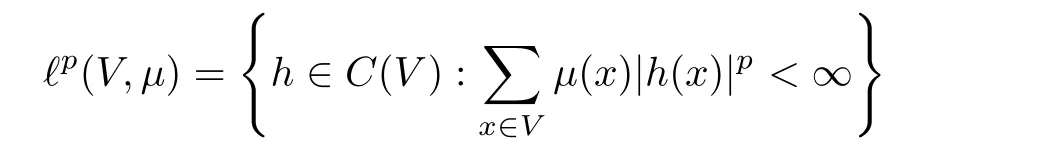
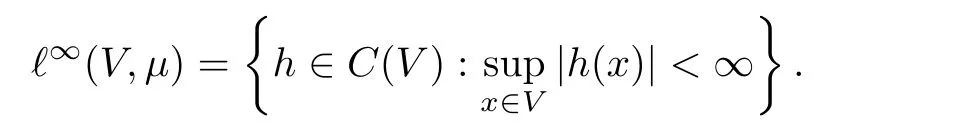
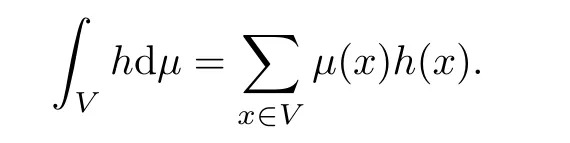
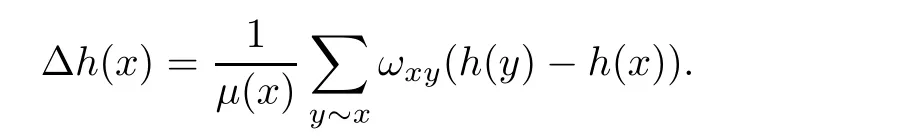
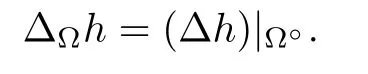
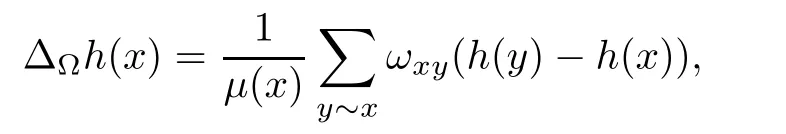
2.2 The volume growth of graphs
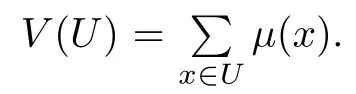
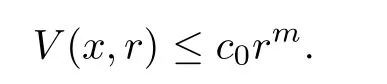
2.3 The heat kernel on graphs

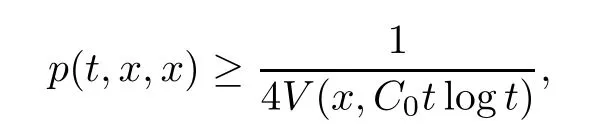
3 Proof of Theorem 1.1



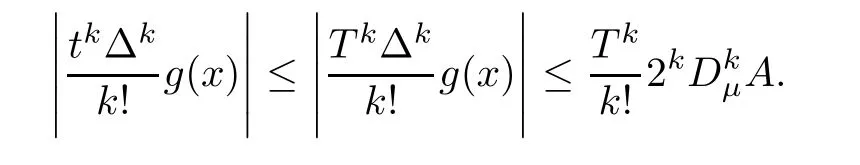

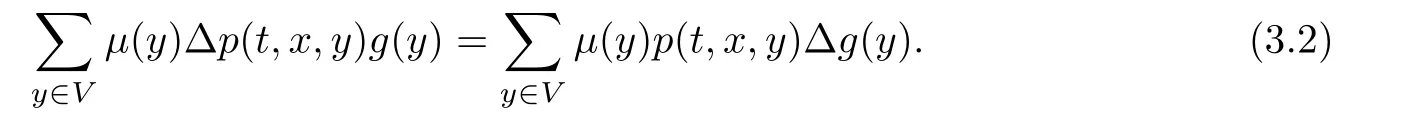

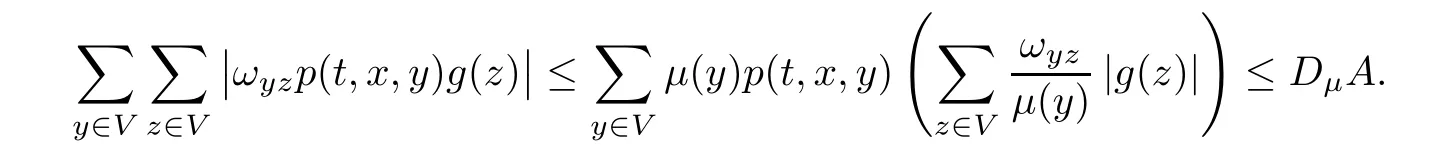
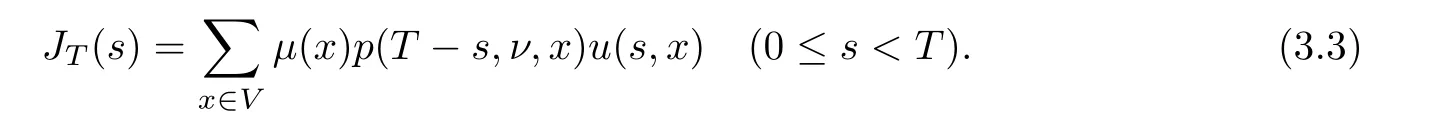

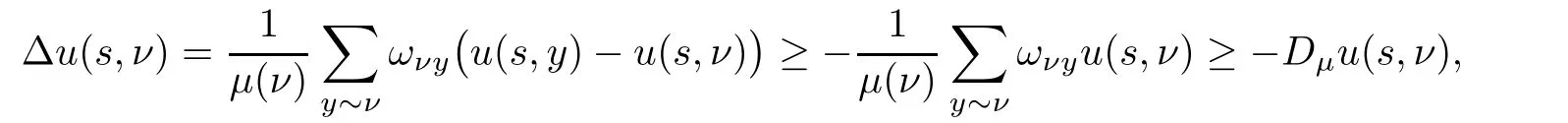
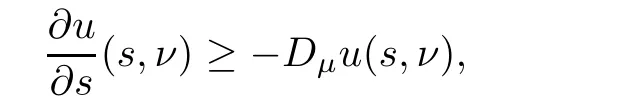

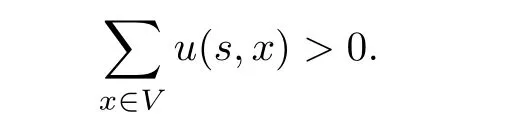






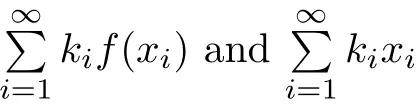

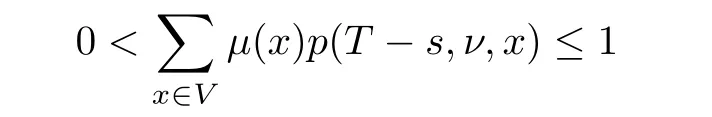

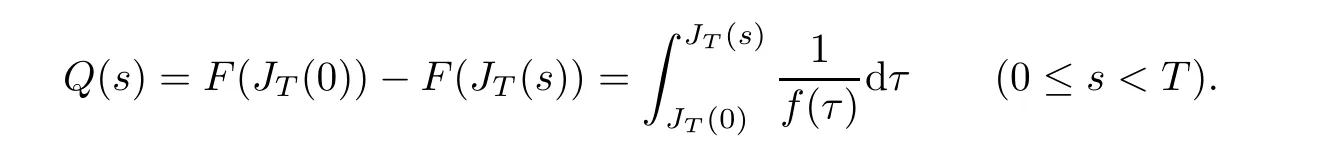
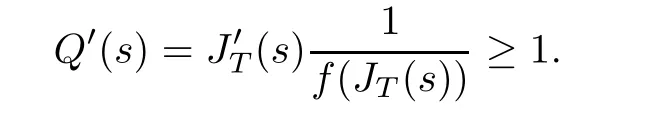

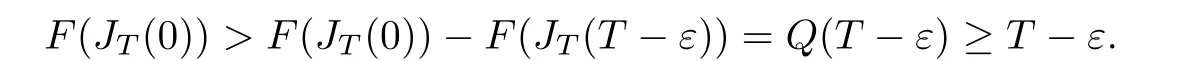

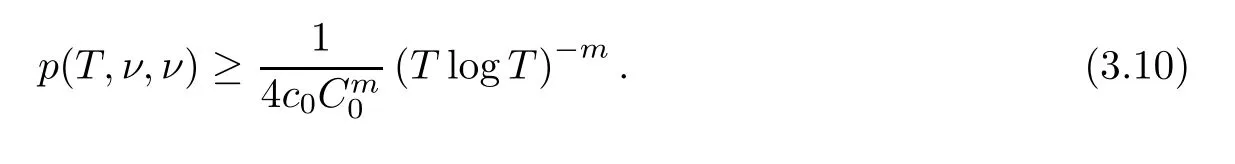



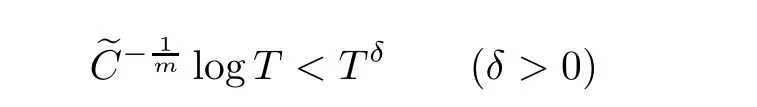
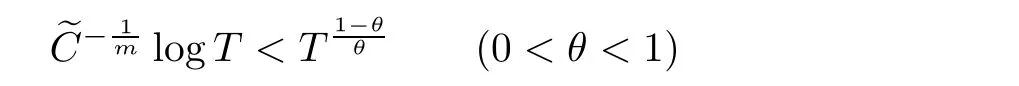


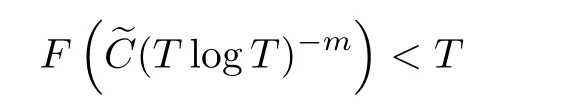
4 Proof of Theorem 1.2
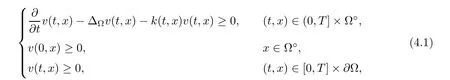
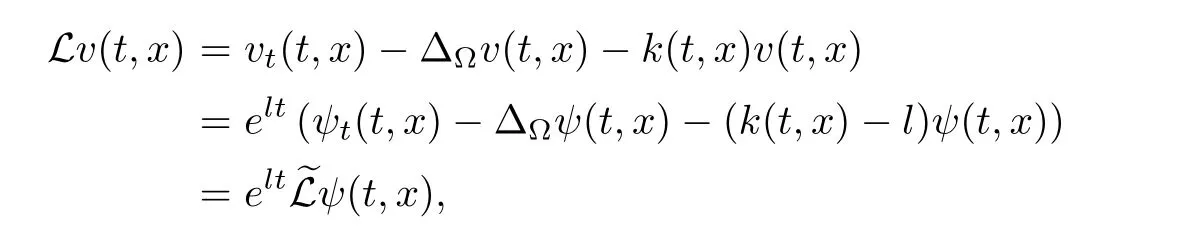
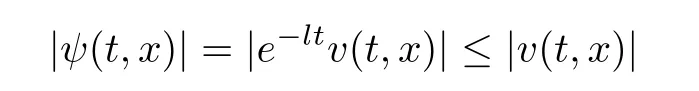
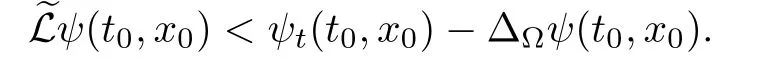

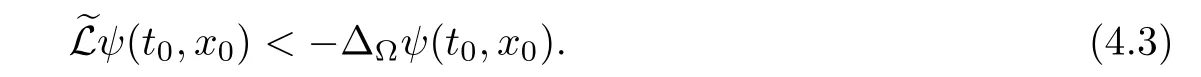


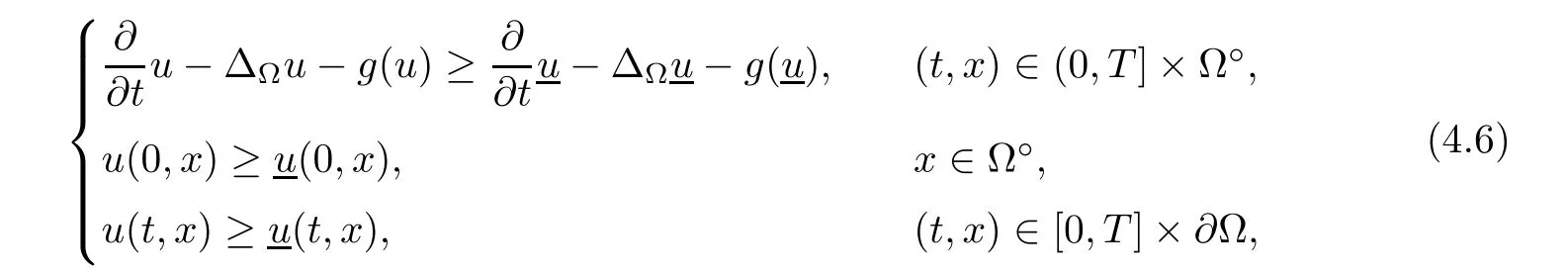

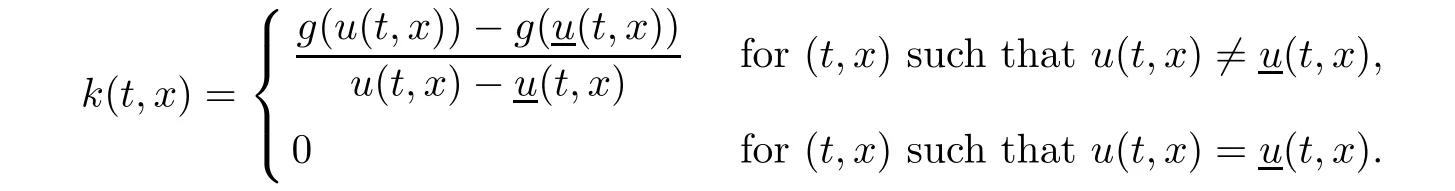
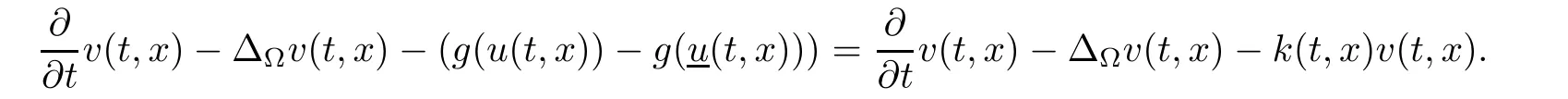
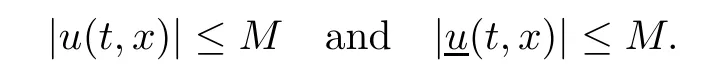
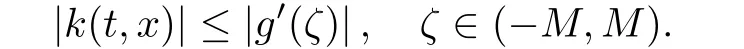

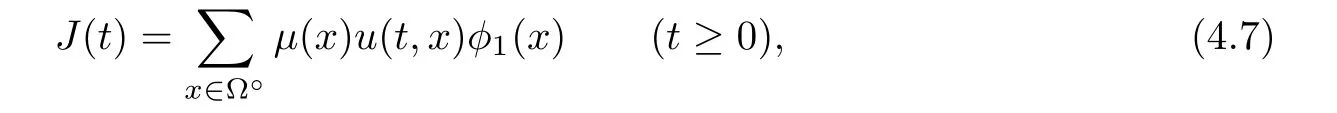
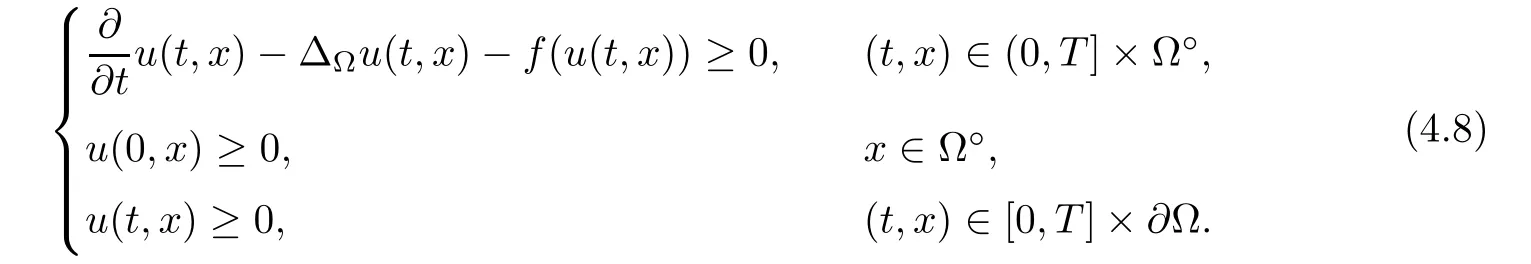
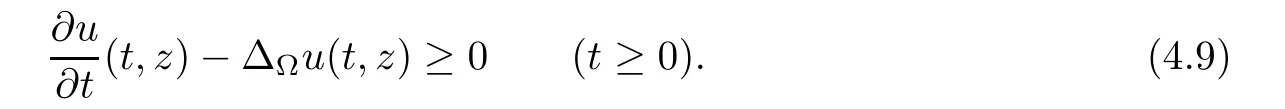
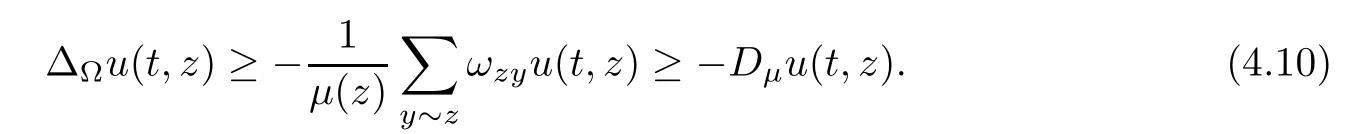


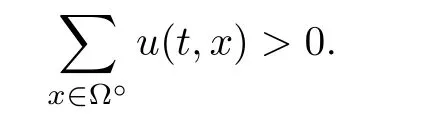


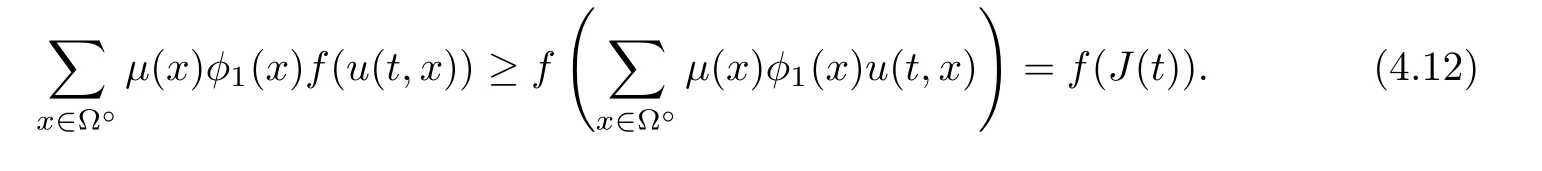


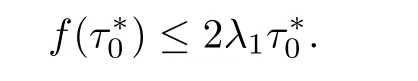

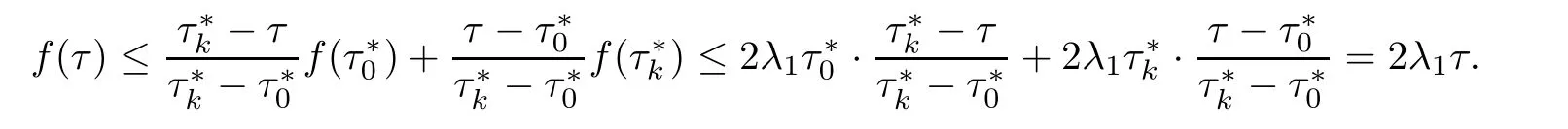



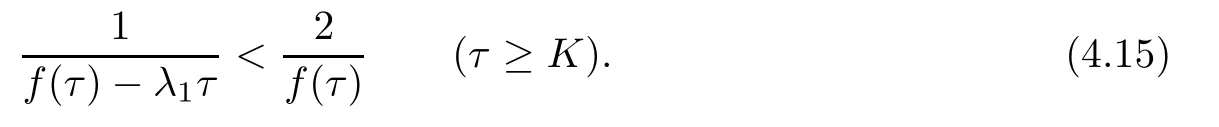



 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
