航空发动机振动不平衡相位检测方法研究
冯健朋,赵小勇
(中航工业西安航空计算技术研究所,西安710065)
1 引言
振动超限是航空发动机等高速旋转机械转子系统的常见故障[1]。航空发动机振动监测系统通过安装在发动机多个部位的传感器来监测发动机振动,以及转子转速和相位[2]。振动采集处理单元通过采集发动机振动和转速信号,利用数字信号处理技术,完成振动信号频域处理、转速跟踪、转子相位基准检测和振动不平衡相位求取。发动机转子配平是降低发动机振动的有效途径[3]。传统的三元法配平,存在开车次数多的缺点。而通过实时求取发动机振动不平衡幅值、相位,利用发动机空中稳态运行时的振动情况在翼确定发动机配平方案,可缩短配平时间、减少地面开车次数,具有较高的发动机转子配平工作效率[4]。
若采用基于发动机振动不平衡相位和幅值的动平衡方法,准确求取发动机振动不平衡相位是保证动平衡效果的关键。传统FFT(快速傅里叶变换)法受频谱泄漏和栅栏效应影响,难以保证不平衡相位检测的精度。整周期截断DFT(离散傅里叶变换)法可有效解决FFT处理时的频谱泄漏和栅栏效应问题,但发动机转速难以保证在理想的稳定状态,且实现整周期采样对硬件的要求大为提高[5],不便于机载实现。时域相关处理法在非周期采样时同样存在误差较大的问题,虽然一些时域相关改进方法可以避免非整周期采样带来的误差[6],但由于发动机振动信号是高低压转子频率信号与多个次倍频及噪声信号的叠加,不具备相移及重构的条件。
鉴于上述各方法存在的局限性,本文提出一种基于互功率谱的航空发动机振动不平衡相位检测方法,对发动机转子相位基准信号进行重构,在发动机振动信号频谱分析的基础上求取互功率谱,消除噪声及不相关信号的干扰,降低运算资源占用,保证了发动机振动不平衡相位检测的准确度;同时,完成了该方法的理论推算和发动机台架试车验证。
2 航空发动机振动不平衡相位
发动机转速信号为带高齿标记的正弦信号,高齿信号可作为发动机振动不平衡相位的基准。航空发动机振动不平衡相位为转子相位基准信号到发动机低压转子基频振动信号峰值之间的角度,如图1所示。图中振动信号为低压转子基频的振动信号。发动机整机振动时域信号含有丰富的频率成分,是高低压转子频率及其次、倍频信号以及噪声信号的叠加[7],转子基频信号淹没其中,如图2所示。理论上可以依据低压转子频率(转速)设计一个窄带滤波器,滤出转子基频振动信号,然后进行相位估计。但转速信号是不断变化的,设计随转速频率变化的带通滤波器比较复杂、难以实现,且在计算资源受限、实时性要求高的机载工程实践中不适用。
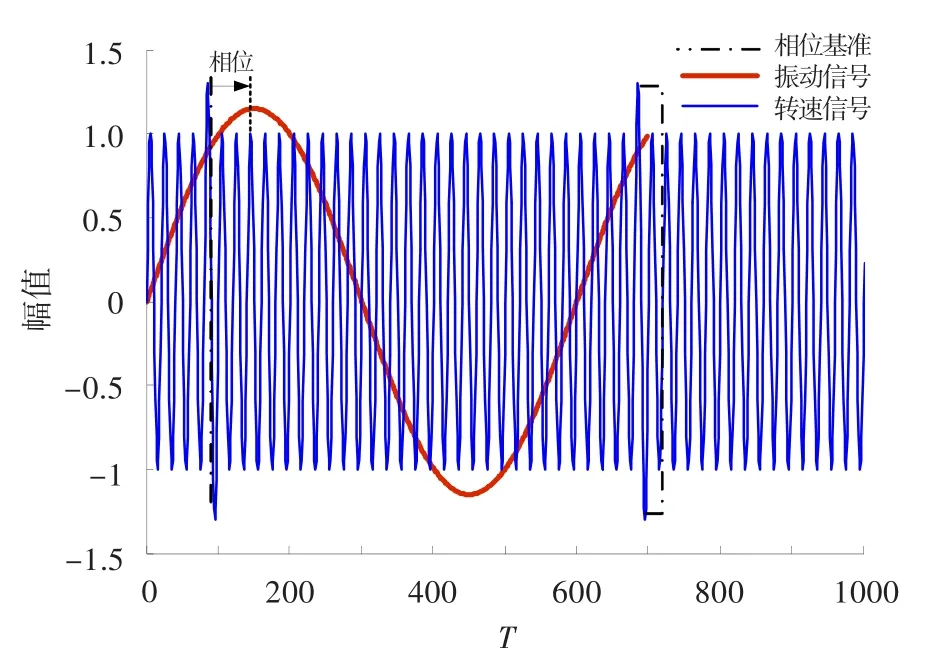
图1 航空发动机振动不平衡相位Fig.1 Aero-engine vibration imbalance phase
3 基于互功率谱的相位估计原理
对两个同频率信号进行互相关,能够起到消除噪声的作用[8]。求取两组信号的互功率谱有间接法和周期图法两种方法。间接法的理论基础是维纳-辛钦定理,互功率谱为互相关函数的傅里叶变换[9]。
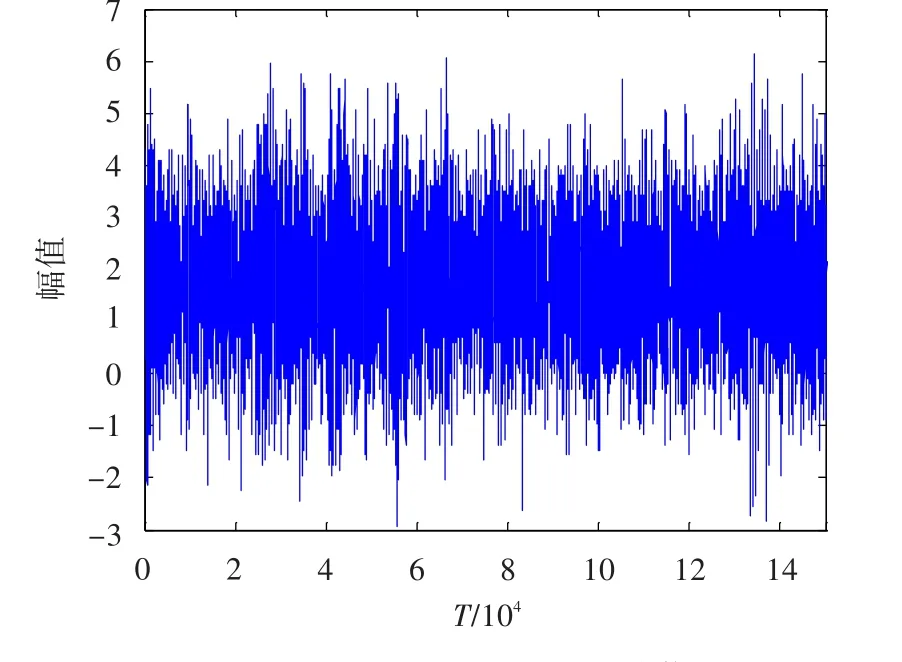
图2 航空发动机振动时域信号Fig.2 Aero-engine vibration signal in time domain
对于两路同频信号:
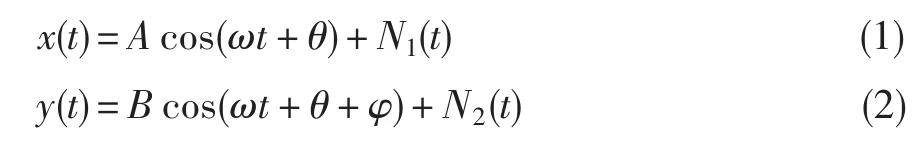
式中:A、B分别为两路信号的幅值,θ和θ+φ分别为两路信号的相位,N1(t)和N2(t)分别为叠加在两路信号上的噪声。
其互相关函数定义为:

当选取(0,kT+ΔT)为数据分析区间时
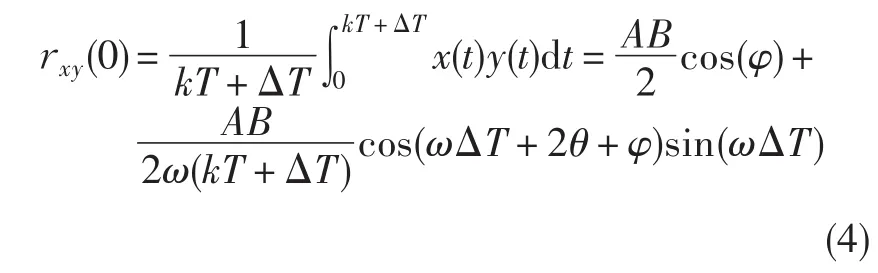
当ΔT=0时,选定的分析数据为整周期
当ΔT≠0时,选定的分析数据为非整周期,但如果分析数据足够长,公式(4)后半部分近似为0,计算的互相关函数与公式(5)一致。
x(t)和y(t)的互功率谱密度为互相关函数rxy(0)的傅里叶变换。

将式(5)代入式(6),得
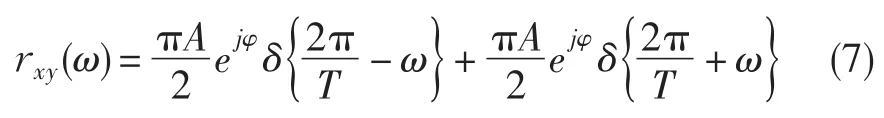
结果中使用了狄拉克函数,该式表明两同频信号的互功率谱密度为两条对称的谱线[10],在处,互功率谱密度为一虚数值,该虚数的相角即为所求相位差。因此,只要得到rxy(ω),通过式(8)就可计算所求相位差。

对应数字化的计算,离散表示为:
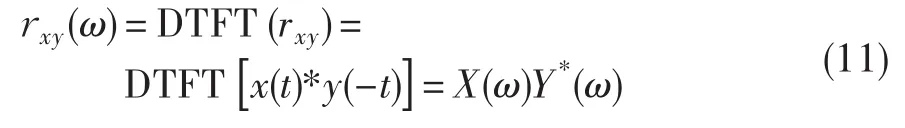
由DTFT离散时间傅里叶变换的时域翻折性可推导,互功率直接法结果与间接法结果一致[11]。由此,可通过直接法计算两信号的互功率谱来求取其相位差。
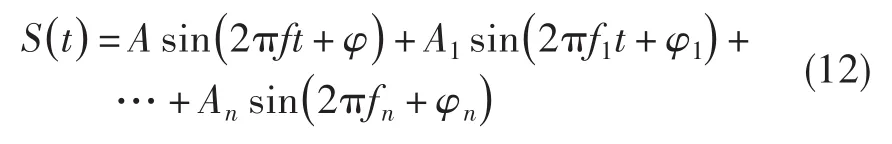
式中:f为发动机低压转子转速基频,f1~fn为发动机振动信号中除低压转子基频外的频率,φ为待求取的相位角。
4 基于互功率谱估计的相位检测方法
图3所示为基于互功率谱估计的航空发动机振动不平衡相位检测法的计算处理流程。
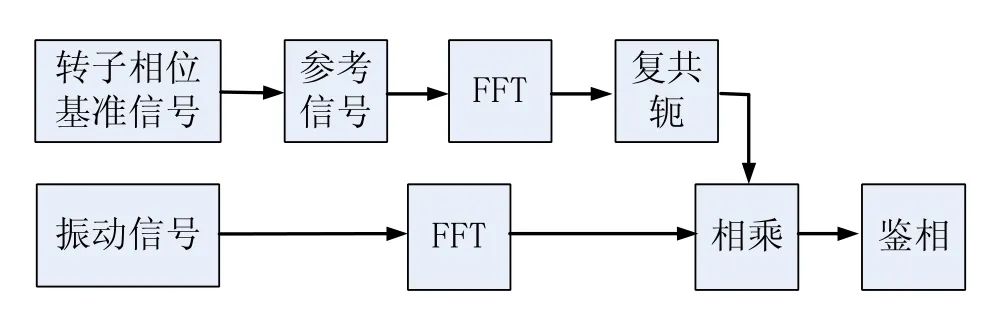
图3 振动不平衡相位检测流程Fig.3 The process of vibration imbalance phase measuring
4.1 转子相位基准信号重构
发动机转速原始信号包含转子的相位基准信息,通过高速硬件电路捕捉转速信号中转子相位基准,形成表示转子相位基准的脉冲信号。求取互功率谱之前,需重构与发动机转速同频的转子相位基准参考信号。具体方法为:记录发动机转子相位基准信号,检测基准脉冲信号;以脉冲信号为起点,提取长度为N的相位基准信号和发动机振动信号,计算相位基准信号中相邻两个脉冲之间的时间Tk;以1/Tk生成同频的正弦信号,得到正弦信号序列X。
4.2 振动信号与转子相位信号互功率谱求取
对振动信号Y和正弦信号序列X分别进行FFT,得到正弦参考序列傅里叶变换X(k)和振动信号序列傅里叶变换Y(k)。按照公式(13)根据正弦参考序列和振动信号序列FFT结果,求取转子相位基准信号与振动信号的互功率谱。

式中:Gxy为互功率谱。
4.3 相位计算
对求取的互功率谱,按公式(14)找出功率谱曲线中发动机转子转速频率附近的幅值最大点,并记录该频率点k。
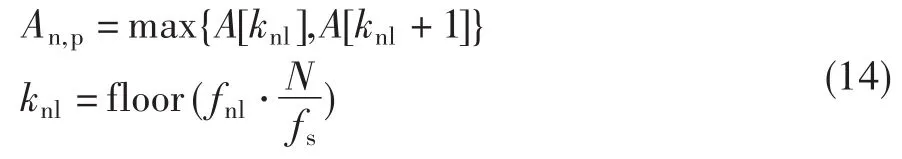
式中:An,p为转子基频处振动加速度峰值;fnl为转子基频;fs为采样频率;N为FFT变换点数;floor(x)为小于x的最大整数。
按照公式(15)提取频率点k处互功率谱的实部、虚部计算相位,该相位就为发动机转子振动不平衡相位,可用于转子振动的配平。
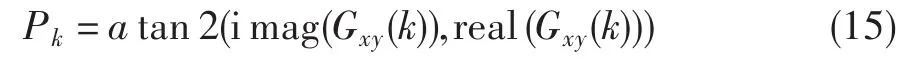
式中:Pk为转子振动不平衡相位,imag(Gxy(k))为互功率谱虚部,real(Gxy(k))为互功率谱实部。
5 发动机试车验证
通过发动机台架试车验证算法的正确性。图4为发动机试车采集的低压转子垂直方向的振动时域数据和低压转子相位基准信号。按照4.1节所述方法,利用图4中转子相位基准信号产生的正弦信号序列见图5。根据公式(13)计算本次发动机试车转子相位基准信号与振动信号的互功率谱,其幅频曲线见图6。图中幅值最大点对应的频率为64 Hz,记录该点的实部、虚部,根据公式(15)计算得到发动机低压转子的振动不平衡相位。
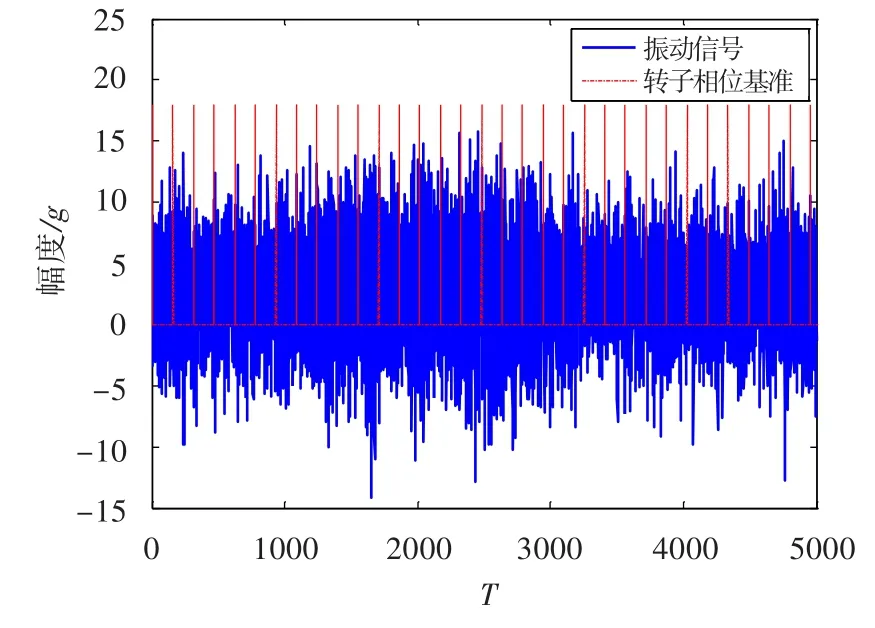
图4 发动机振动及转子相位基准信号Fig.4 Engine vibration and rotor phase base signal
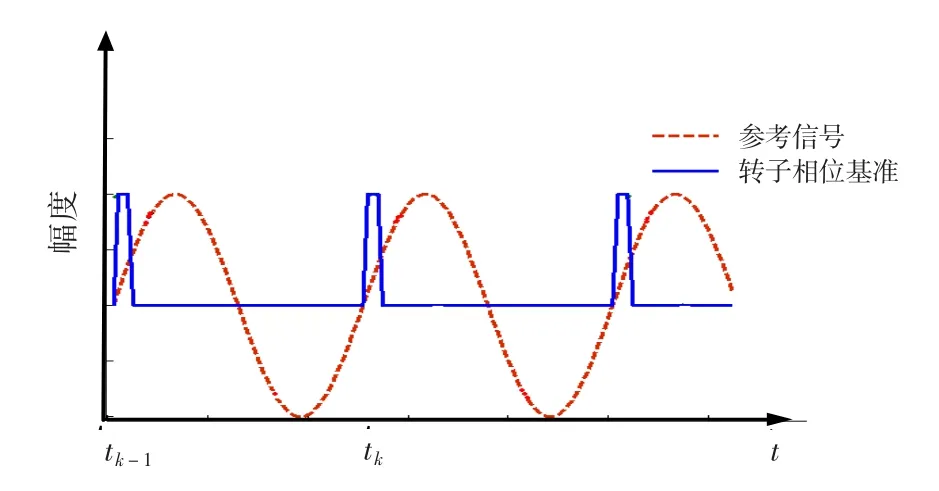
图5 子相位基准信号及其参考信号Fig.5 Rotor phase base signal and reference signal
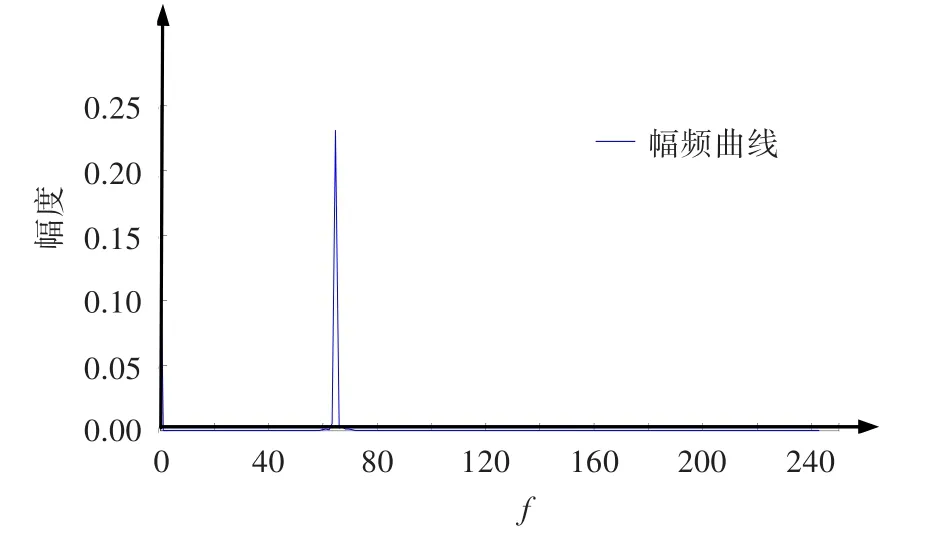
图6 发动机转子相位基准信号与振动信号的互功率谱Fig.6 The cross spectrum between vibration and reference signal for rotor phase
图7为发动机台架试车所获得的转子不平衡相位角。为进一步验证该转子不平衡相位检测法的正确性和工程适用性,使用该方法计算的相位角通过影响系数法进行发动机转子振动配平[12]。具体过程为:①将图7记录的4个转速点的不平衡相位及基频振动量值作为第一遍试车参考;②在发动机配平螺钉中标记一点为零点,并在零点处假装配平螺钉,进行第二遍试车,记录与图7相同的4个转速点不平衡相位及转子基频振动量值;③根据公式(16)利用两次试车的振动数据计算振动不平衡影响系数;④根据公式(17)利用初始振动量和计算的不平衡影响系数求取配平质量和角度。
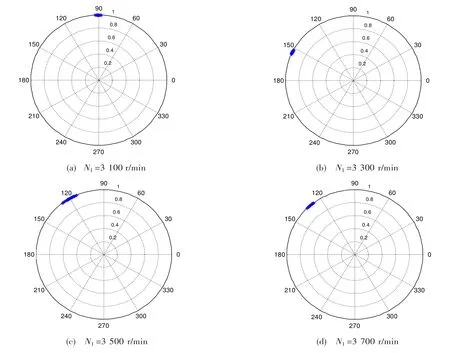
图7 试车试验得出的发动机转子振动不平衡相位Fig.7 The engine rotor vibration imbalance phase measured from engine ground test

式中:为影响系数;0为初始振动量;1为试重运行时的振动量;为增加的试重大小和角度;为配平需增加的配平量,包括配重的质量和角度。
表1示出了发动机配平前后振动量值的变化,证明该相位检测方法求取发动机转子不平衡相位正确有效,能够用于发动机振动配平的工程实践中。
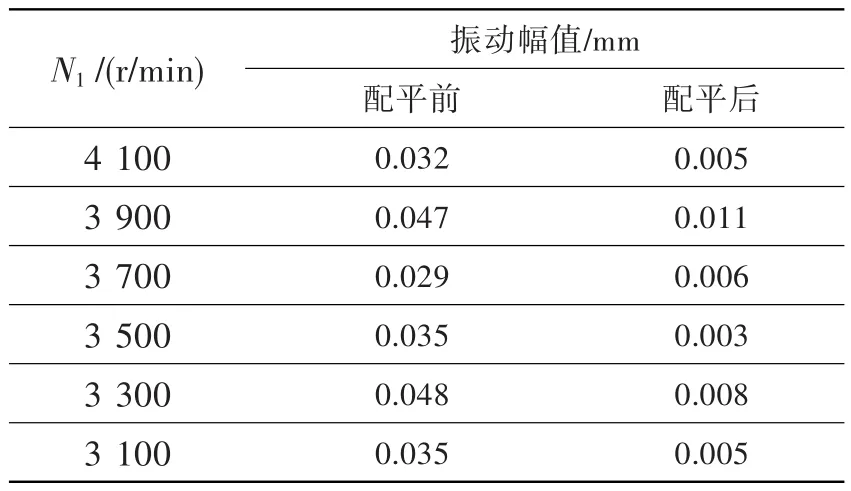
表1 发动机配平前后振动大小变化Table 1 The vibration variation before and after engine balancing
6 结论
从互功率谱原理出发,提出一种基于互功率谱的航空发动机振动不平衡相位检测方法。经发动机台架试车验证证明,该方法完全适用于航空发动机等燃气涡轮机械的转子配平,且软件实现简单,实时性好,对提高发动机的维护性和运营保障效率具有重要作用。

