土壤和地下水环境中纳米材料迁移的研究进展
代朝猛, 沈 晖, 段艳平, 刘曙光
(1.同济大学 土木工程学院, 上海 200092; 2.上海师范大学 城市发展研究院, 上海 200234)
1 研究背景
从20世纪80年代至今,纳米科学与纳米材料一直是最热门的科学研究领域之一,被誉为“二十一世纪最有前途的材料”[1]。纳米材料作为一种重要的新型材料,由于其特殊的理化性质,即小尺寸效应、界面(表面)效应、量子尺寸效应以及量子隧道效应等[2-3],被越来越来多地应用于医药学、污染土壤的修复、污水处理、农业肥料等诸多领域[3-6]。而纳米材料的广泛应用意味着其在生产、使用、废弃处理等每一个环节都可能会不同程度地被释放到自然环境中。而土壤与地下水环境(以下简称“地下环境”subsurface environment)是几乎所有环境污染物主要的蓄积库与归宿地,纳米材料进入此环境后,其本身运移所带来的生态环境风险不可忽视,比如某些纳米材料本身具有生物毒性,可能作用于生物体并造成不可预计的后果[7-9];同时由于其特殊的结构能够吸附携带其他污染物协同运移[10-11],因而研究纳米材料在地下环境中的运移规律,对于定性和定量研究包括纳米材料在内的各种污染物在地下环境中的迁移、土壤与地下水环境保护以及评估生态环境风险具有重要意义。
2 纳米材料的分类
纳米材料是指三维空间尺度至少有一维处于纳米量级(1~100 nm)的材料。纳米材料按照基本单元的维数可分为三类:零维(也叫量子点) ,如纳米尺度颗粒、原子团簇等;一维(也叫量子线) ,如纳米线、纳米管、纳米棒等;二维( 也叫量子阱) ,如超薄膜、多层膜、超晶格等[12]。
纳米材料主要可分为以下4类:碳基纳米材料、金属纳米材料、聚合纳米材料和半导体纳米材料。
(1)碳基纳米材料是纳米材料中应用最为广泛的一类,其研究热点主要集中于碳纳米管、石墨烯、富勒烯[13-16]。其中碳纳米管又可分为单壁碳纳米管和多壁碳纳米管。碳纳米材料拥有高比表面积、高热导率、高电导率、高稳定性、高化学惰性、低密度等特点被广泛应用于气体吸附、水净化催化载体、电化学双层电容器、太阳能电池等领域。
(2)金属纳米材料主要分为两大类:一类是金属氧化物纳米材料,如纳米二氧化钛颗粒,纳米氧化锌等;另一类是金属单质纳米材料,如纳米铁、纳米银等。纳米零价铁被应用于环境修复领域[17-18],纳米银被广泛应用于除菌产品[19]。
(3)聚合纳米材料主要用于药物传输和治疗,在代谢和免疫毒性等医疗干预中有着广泛的应用[20-22]。如脂质聚合物纳米材料可以作为某些药物的载体用于医疗[21]。
(4)半导体纳米材料也被称作量子点,具有纳米晶粒和高浓度晶界两大特征,可由单种或多种半导体材料合成,常见的有纳米硅、纳米硫化锌等[23-25]。
3 纳米材料在地下环境中的迁移
地下环境中的胶体常处于热力学和动力学的不稳定状态,地下环境中物理化学条件如地下水流速、pH、离子强度等的改变会显著影响胶体自身的团聚-分散,影响胶体在多孔介质中的对流-弥散、吸附-解吸、滤除、堵塞、阻塞等过程,从而影响胶体在多孔介质中的迁移。纳米材料由于其水力学直径大都在1 nm~1 um范围内,在胶体科学定义范围内,因而可以用胶体科学的理论来解释纳米材料在地下环境中运移行为。
3.1 纳米材料迁移的理论
控制胶体稳定性最主要的两种相互作用力是范德华力和双电层力,以这两种力为基础的描述胶体稳定的理论即DLVO(Derjaguin-Landau-Verwey-Overbeek)理论,被用来解释胶体的解析与吸附。DLVO 势能图一般横坐标为胶体与固相颗粒之间的间隔距离,纵坐标由两者之间的相互作用能(范德华能和双电层势能之和, ФT)构成(图1)。当胶体和固相颗粒表面的电荷性质相同时(均为正或负),双电层力为排斥力,在胶体与固相颗粒之间的相互作用距离由小增大的过程中,DLVO 势能曲线依次为初级势阱(Фpri),排斥势垒(Фmax),次级势阱(Фsec)。不同纳米材料沉积时处于不同势阱中,纳米银沉积时只有10%是处于次级势阱[26]而纳米二氧化钛沉积则主要是在次级势阱中[27]。虽然有文献指出当纳米材料有足够能量越过排斥势垒,沉积处于初级势阱,这种沉积是不可逆的[28]。但是基于当前扩展DLVO理论,初级势阱的深度是有限的,因此被吸附到初级势阱中的纳米材料仍旧存在被释放出来的可能。
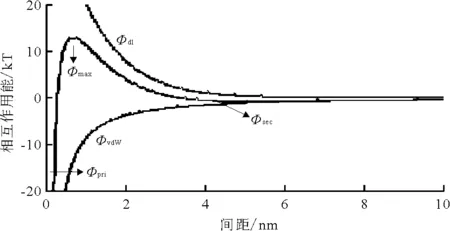
图1 DLVO势能图
胶体过滤理论则是被广泛运用于描述胶体沉积过程的理论[29-31]。胶体过滤理论认为,胶体粒子沉积到固相颗粒表面取决于拦截、重力沉降和布朗扩散3种机制(图2)[32]。粒径较大的粒子或者团聚的胶体主要因拦截与重力沉降的机制沉积到固相颗粒表面,而纳米材料沉积机制以布朗扩散为主。但是当其发生团聚时沉积机制也会随之改变[33]。
上述理论是基于胶体科学提出的,大部分实验现象可以被合理解释。但是传统DLVO理论未考虑除了范德华力与双电层力以外的纳米材料与固相颗粒,如水合力、氢键作用力、疏水力等力,而胶体过滤理论则忽视纳米材料表面粗糙性、表面电荷非均质性、纳米材料和固相颗粒的物理和化学性质的非均一性等。虽然目前扩展DLVO理论,经修正的胶体过滤理论已经对这些影响因素进行了研究,但是纳米材料在土体中运移机理仍存在缺陷,需要进一步的探索和研究。
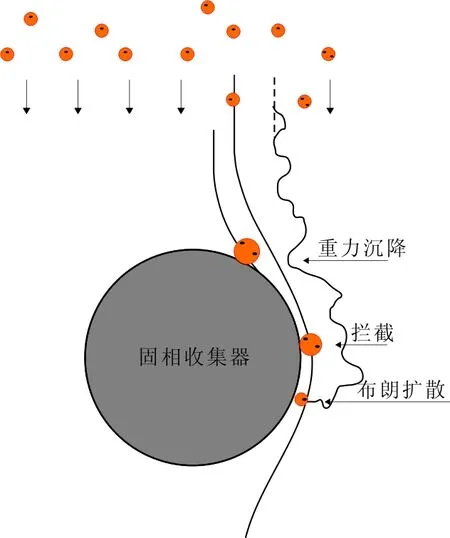
图2 胶体的3种沉积机制
3.2 纳米材料迁移的数值模拟
应用数学模型可以定量直观地将纳米材料在地下水中的迁移过程进行数学表达。地下水中的溶质的迁移,以运动的地下水为载体,在几何结构非常复杂的空隙空间进行,这一过程中既发生溶质的对流、扩撒,机械弥散以及土壤基质对溶质的吸附解吸,也有溶质本身的一系列化学反应。因此首先仅考虑对流、扩散,机械弥散的作用,纳米材料在一维情况下的运移可以用对流-弥散方程来描述[34-37]:
(1)
式中:θ为有效孔隙度;C为液相中纳米材料浓度;S为固相中纳米材料的浓度;t为时间;ρ为多孔介质密度;x为距离;D为水动力弥散系数;q为孔隙水流。方程左边第一项表示液相中纳米材料浓度的变化速率,第二项表示固相上的纳米材料浓度变化速率,即吸附项。方程右边两项分别为水动力弥散项和对流项。方程中吸附项用不同的方程可以得到不同的迁移模型。
平衡吸附模型。物理化学吸附包括可逆吸附和不可逆吸附,可逆吸附通常用平衡吸附或动力学吸附来表示,而不可逆吸附通常用一阶动力学方程来表示。早些的模型通常只考虑平衡吸附。若平衡吸附符合等温吸附方程,纳米材料的吸附可以用不同的等温吸附方程来描述,并且可以将不同吸附方程组合来表达[38]。下面方程描述了基于等温吸附方程,达到吸附平衡时,固相中纳米材料的浓度,即:
(2)
式中:ks为平衡常数;η为Langmuir平衡常数;βi为Freundlich平衡常数;ks=0表示纳米材料不吸附至固相;βi=1表示只发生Langmuir吸附;η=0表示只发生Freundlich吸附;当βi=1且η=0表示纳米材料吸附只与液相浓度和平衡常数有关。
双位点模型[39-40]。根据纳米材料沉积位点差异,利用双位点模型,将起固相中纳米材料浓度分为吸附与阻塞两类来讨论。通常双位点模型要比平衡吸附模型具有更好的模拟效果。双位点模型如下:
S=Satt+Sstr
(3)
(4)
(5)
(6)
(7)
(8)
式中:Satt为固相中吸附的纳米材料浓度;Sstr为固相中阻塞的纳米材料浓度;ψatt为量纲-纳米材料吸附函数,用于校正吸附曲线的曲率,并考虑到熟化和非指数空间分布,由Langmuirian方法得出[41-42];Smax为固相中吸附纳米材料最大浓度,受纳米材料与固相颗粒静电作用和流体动力学因素影响;katt为吸附系数;kdet为解吸系数,有实验指出在纳米材料迁移过程中,其影响可以忽略[43];θw为含水率;dc为固相颗粒平均等效直径;vp为孔隙水流速;η0为单一位点接触效率(single-collector contact efficiency)等;α为碰撞效率,表示发生接触的纳米材料发生的沉积概率;kstr为阻塞系数;ψstr为量纲-纳米材料阻塞函数;x0阻塞开始发生位置,通常土柱试验取进口处;β为用于控制曲线形状的经验拟合参数,有大量试验围绕β取值与纳米材料的迁移行为展开取得一系列的成果[36,44-46]。
基于方程(1)~(8),纳米材料在饱和多孔介质中的迁移可以用不同模型来表达。Zhang Lunliang等[47]用3种模型模拟了富勒烯的穿透曲线,分别是:(1)将katt、kstr和Smax作为拟合参数的双位点模型;(2)katt和Smax作为拟合参数的改进过滤理论模型;(3)只将katt作拟合参数的胶体过滤理论模型。Kasel等[44]则用以下4种模型模拟了MWCNT的穿透与滞留曲线:(1)通过设定ψatt·ψstr=1的吸附、解吸模型;(2)当β=0时的吸附、解吸、Langmuirian堵塞模型;(3)当β=0.765,ψatt取较大值的依赖于距离的滞留模型;(4)当β=0.765,ψatt<1,依赖于时间与距离的滞留模型。
3.3 影响纳米材料迁移的因素
3.3.1 纳米材料自身理化性质 纳米材料本身的表面化学性质与电性是影响其在地下水环境中迁移的重要因素。通常来说带有亲水型的官能团的纳米材料拥有更高的流动性,而疏水型则更容易发生团聚与沉降。Lecoanet等[48]发现通过富勒烯羟基化反应得到的富勒醇更容易通过饱和多孔介质。土壤颗粒通常带负电荷,由于带负电荷的纳米材料与土壤颗粒之间的静电斥力,使其在地下水环境中更易流动。相反的,带正电的纳米材料通过静电引力被吸附到土壤颗粒表面而固定下来。Kim等[28]的实验结果表明4%的带正电的纳米零价铁在通过带负电石英砂土柱时会沉积下来。因此为了提高或者抑制纳米材料的流动性,研究者通常以表面活性剂或高聚合物修饰纳米材料用以改变其表面性质[49-53]。
3.3.2 地下环境中固相性质 土壤介质是地下环境的主体,纳米材料进入地下环境后在其孔隙间运动,因此大量学者探究了土壤基质的种类、粒径等对纳米材料的运移性能的影响。就土壤基质种类而言,纳米材料在玻璃珠中运移性能明显高于石英砂,当土体黏土含量越高时运移性能越差。Wang等[54]的研究表明玻璃微珠填充土柱可滞留8%~49%注入的nC60,而渥太华砂填充的土柱滞留率高达77%;Kanel等[55]通过试验发现加入吐温20的纳米铁在玻璃珠中运移性能高于石英砂。Yang等[56]发现由聚丙烯酸改性的纳米铁可以轻易穿透石英砂柱,但不能穿透壤质砂柱。
另外Mattison等[57]在研究相同条件下,碳纳米管在不同粒径石英砂中运移性能时发现石英砂粒径减小,碳纳米管运移性能减弱。并且纳米银、纳米二氧化钛也有此规律[58-59]。
3.3.3 地下环境中液相性质 地下水中pH、离子强度、水动力条件以及溶解性有机质(DOM)与表面活性剂等也会对纳米材料的迁移造成影响。
研究表明pH通过影响纳米材料Zeta电位来影响其的流动性,当pH接近零电点时(PZC),体系Zeta电位降低,纳米材料容易发生团聚,因而运移受到抑制[60-61]。Lanpheve等[62]发现当pH值由4.0降到2.0时,氧化石墨烯的平均电泳淌度明显降低,表面的静电斥力减弱,水力学直径急剧增大,移动性降低。
不同研究者在研究不同纳米材料如氧化石墨烯、富勒烯、单壁碳纳米管时都发现随着离子强度的升高,纳米材料运移性能降低[63-65]。其原因在于离子强度控制着纳米材料与介质颗粒间以及其本身之间的静电作用力,通过引起扩散双电层电势的变化影响其沉淀动力学过程,在低离子强度下,纳米材料扩散双电层较厚,扩散双电层排斥力升高,有利于保持稳定并促进的运移,高离子强度则相反[66-67]。离子强度与沉积率可以用以下公式表示[66]:
(9)
式中:CS为离子浓度;CDC为纳米材料的临界沉积浓度;β为纳米材料对离子浓度变化的敏感度系数。
纳米材料在地下环境的运移受到水动力条件变化的影响,其迁移行为会随着扰动强度的变化而变化,但是流速变化对纳米材料在地下环境中的迁移并不是确定的。Liu等[68]和Li等[69]的实验结果表明流速越高,富勒烯与多璧碳纳米管在多孔介质中移动越快;Lecoanet等[48]的实验结果却呈现相反的结论,原因在于碳基纳米材料沉积速率到达与流速无关的水平,但是流速对金属氧化物纳米材料迁移的机理仍不明确。
研究表明当地下水中含有DOM时,纳米粒子在多孔介质中的迁移性得到增强,其原理在于通过表面修饰纳米材料增强与固相颗粒静电斥力与空间位阻力,增强了纳米材料的分散性[53,70-71]。表面活性剂作用于纳米材料的机理与DOM作用类似,但其迁移性取决于静电斥力、空间位阻力等与纳米材料团聚和分散哪个在迁移过程中起决定作用。
Wang等[72]试验表明加入表面活性剂SDBS的纳米羟基磷灰石移动性增强,而加入CTAB的移动性减弱。
4 结论与展望
(1)尽管DLVO理论的应用有利推动纳米材料迁移研究的发展,而用过滤理论来描述纳米材料的沉积过程也符合大多数试验结果,但是纳米材料与固相颗粒之前的非DLVO力如水合力、氢键作用力、疏水力等也起着不可忽视的作用,过滤理论忽略的纳米材料表面粗糙性、表面电荷非均质性、纳米材料和固相颗粒的物理和化学性质的非均一性等极大地影响该理论的应用。今后还需要针对以上问题加强对纳米材料在地下环境中沉积运移实验研究,对其机理进行探讨,进一步优化和完善DLVO理论与胶体过滤理论。
(2)近年来有关纳米材料在地下环境中迁移的数值模拟研究,结合了对流弥散理论和胶体过滤理论的数学模型得到快速发展,但纳米材料迁移模型涉及到众多水文地质参数和有关纳米材料本身的特征参数,因此模型中相关参数的选取、参数敏感性分析以及模拟结果的准确性还有待于进一步探讨和验证。
(3)当前关于纳米材料在地下环境中迁移的研究多以实验室模拟运移过程进行,而针对实际地下环境的研究鲜有报道。在实验室内理想实验条件下得出的结论有一定代表性,但是并不能完全符合复杂的真实地下环境情况,所以今后有必要开展实际的野外场地研究。
(4)目前针对纳米材料在地下环境中迁移研究大多集中在对结果的表观描述上,并未对其机理解释清楚,也未形成统一的理论体系。因此,应当综合利用多种分析和表征手段,从微观层面上阐明机理,结合土壤-地下水系统的概念模型,进一步形成完整而系统的理论体系。

