光伏板清洁装置横臂轻量化设计方法
杨世强, 侯玉庆(西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048)
光伏板表面清洁度对其发电效率有重要影响[1],表面积灰的光伏组件工作时,其发电效率会降低10%到25%。实现清洁装置的低成本与高效率运行具有重要的现实意义与经济价值。最初人们使用水枪或者人工使用滚刷、清洁布等清除表面灰尘[2],近年来随着科技的发展,出现了很多自动化大型清洁设备,比如移动装置搭载盘刷或滚刷设备的大型移动清洗车,具有较高的清洁效率[3],但是其结构普遍笨重复杂,成本较高。大型清洁装置普遍由移动装置、机械臂装置以及末端执行部分(通常为盘刷或者滚刷)等组成[4],由于机械臂的尺寸和结构对于清洁装置自身性能影响很大[5],因此,如何通过结构优化实现轻量化设计并保证其足够的力学性能,对机械结构设计来说具有重要意义。
机械结构优化设计是将最优化理论和结构设计相结合,借助现代计算方法,从一系列受约束的可行解中寻求使某一目标最大或最小的参数组合,从而使设计质量得到提高[6]。为提升产品性能,降低产品耗材及成本,提升企业竞争力,国外很多大型企业在产品设计中已广泛地运用结构优化技术。易继军[7]采用拓扑优化方法对数控螺旋锥齿轮机床进行优化,进一步改进了机床的性能。赵伟基[8]对机器人手臂进行分析和优化设计,找出了机械臂的薄弱环节,通过在两个分型面处加装缓冲器,减小了应力集中,减轻了手臂重量。丁渊明[9]对6自由度串联弧焊机器人进行分析,根据其机械臂的特点,提出了工作空间体积和特定区域的能量消耗两个性能指标,以二者为优化目标建立优化模型,利用遗传算法优化弧焊机器人机械臂的结构参数,使得机器人在焊接过程中能量的消耗得以降低。李钊等[10]采用拓扑优化方法对履带架结构形式进行合理布局,改善载荷传递路径以充分发挥材料力学性能,从而提高履带架的承载能力。
针对大型光伏发电厂的光伏板清洁问题,本文开发设计了一种光伏板清洁装置,完成了清洁装置的结构与性能分析。在此基础上,结合清洁装置运行试验,对其关键部件进行拓扑优化设计,分析对比各优化方案的力学性能,为清洁装置的进一步优化提供指导。
1 光伏板清洁装置
为了解决光伏板积灰问题,设计开发了光伏板清洁装置,对光伏组件表面灰尘覆盖层进行及时清理,方案如图1所示。清洁装置主要分为清洁头架和臂架两部分,横臂1和支撑臂2、驱动臂3组成臂架,4为支撑,5为清洁头架。清洁头架是清洁装置的末端执行元件,安装在横臂末端。清洁装置安装在履带式移动平台之上,可实现连续排列的光伏板的清洁作业。臂架部分采用铰接平行四杆机构,驱动臂3转动带动清洁头架实现伸出和收回运动,清洁头架始终保持与光伏板平行的固定姿态,清洁头架安装喷水装置和旋转毛刷实现积灰清理。为减轻重量,清洁头架采用工业铝型材组装而成,毛刷通过电机驱动。
图2(a)为臂架部分的总体设计图,平行四杆机构两条边的长度分别为903.8 mm和330 mm,清洁头架初始姿态与水平面成40°夹角,沿长度方向与光伏板安装倾角一致,宽度方向与光伏板存在一夹角,可微调。清洁装置安装在履带式液压驱动移动平台上。
前期完成的臂架实物如图2(b)所示,根据现场装配和试验结果,现有清洁装置重量较大,移动平台负载较大。横臂前端安装清洁头架,是悬臂梁结构。横臂质量为65.02 kg,约占臂架质量的一半,对其拓扑结构进行优化,减轻自身质量,对改善清洗头工作性能有重要意义。

图2 臂架示意图Fig.2 Schematic diagram of beam
2 横臂的拓扑结构优化
2.1 优化方案
分析横臂受力情况,横臂的末端处两侧面受到清洁头载荷的作用力,约1200 N,工作行进中受到由于盘刷刷毛与光伏板摩擦产生的与前进方向相反的水平方向阻力,约300 N。正常的固定位姿清洁工作中,横臂后端的两个铰接处固定。在Pro/Engineer环境中建立横臂模型,导入有限元分析软件ANSYS系统,材料为45号钢。
因此,在ANSYS环境中,固定约束横臂的圆孔连接面,在横臂的末端两侧面分别施加沿Z方向各600 N作用力模拟清洁头的重力,沿X方向施加300 N作用力模拟工作时受到的刷毛摩擦力,约束和载荷如图3所示。

图3 约束与载荷图Fig.3 Constraints and load diagram
以重量最轻为优化目标,设置质量去除百分比为35%。求解完成后得到如图4所示的拓扑结构和6个主要的可去除区域。

图4 可去除区域与保留区域Fig.4 The removable area and reservation area
结合图4的结果,考虑到加工以及应力集中等情况,本文设计三种优化方案。各方案对前5个区域采用相同减重方式,对区域6设计不同减重孔,如图5所示。对于区域1和2,如图5(a)所示,直接去除1区域并缩小2区域尺寸;在区域3、4和5中设计一个矩形去除区域,边缘倒角处理,如图5(b)和(c)所示。对于区域6采用三种不同减重孔设计:①去除较小部分建议区域,两侧面去除区域为一个支撑,形成方案一,如图5(d)所示;②去除面积加大,侧面去除区域为两个支撑连接,形成方案二,如图5(e)所示;③方案三去除部分与方案一类似,但不设置连接上下面的支撑,如图5(f)所示。方案一去除率为26.5%,方案二去除率为29.53%,方案三去除率为26.84%。

图5 三种优化方案模型Fig.5 Three optimization scheme models
2.2 优化前后静力学对比分析
计算求解的结果只能作为参考[11],需考虑应力集中等因素对改进结构的影响,使用有限元分析软件进行力学分析对比,以检验方案是否可行。对优化前后横臂的力学性能是否满足基本需求进一步分析,约束、载荷的施加方式同图3,在沿Z方向两侧面各施加600 N重力,沿X方向施加300 N摩擦力。计算各方案对应的横臂最大位移、最大应力和质量,如图6所示。

图6 各方案最大位移、最大应力及质量对比Fig.6 Graph comparison of maximum displacement,maximum stress and mass of each scheme
由图6可知,各方案在三个方向的位移相较于原方案,都有不同程度地增加,其中方案一的增量最小,分别为0.5655 mm(X向)、0.1059 mm(Y向)和0.1420 mm(Z向);方案二在Y方向和Z方向的增量最大,各向增量分别为1.2743 mm(X向)、0.3063 mm(Y向)和0.7535 mm(Z向);方案三在Y方向和Z方向的位移均介于方案一与方案二之间,且其变化量更接近于方案二,而在X方向较原方案位移增量最大,为1.6247 mm。总位移增量方案一最小,方案三次之,方案二最大,各向总位移增量分别为0.3294 mm(X向)、1.2130 mm(Y向)和1.0369 mm(Z向)。应力的变化与总位移的变化类似,应力增量方案一最小,方案三次之,方案二最大;方案一二三相较于原方案的应力增量分别为6.574 MPa、34.31 MPa和10.032 MPa。各方案的减重效果方案二最佳,方案一与方案三相当,方案一二三的减重量分别为17.24 kg、19.20 kg和17.45 kg。经过各方案的对比,方案一的最大变形和最大应力都比较小,最大位移位置位于横臂末端边缘,最大应力位置位于去除区域的过渡孔处,如图7所示;方案二的位移和应力都是最大,方案三居中。

图7 方案一总位移与应力云图Fig.7 Total displacement and stress cloud diagram of the scheme one
2.3 优化前后扭转力学分析
实际工作中,由于工作时毛刷与光伏板间的摩擦力作用在横臂末端,横臂的弯曲结构引起扭矩力臂,横臂存在水平方向的扭矩,在此对各方案扭转力学性能进行分析。当X方向分别施加600 N和900 N的摩擦力时,各方案最大变形和最大应力计算结果如图8所示。

图8 扭转工况下各方案最大位移和应力对比Fig.8 Gragh comparison of maximum displacement and stress of each scheme with torsion
对比各方案变形情况可知,三种方案的位移相对于原方案均有一定程度地增加,载荷一定的情况下,方案一、方案二和方案三的最大位移量依次增大,600 N作用下,其相对于原方案的增量依次为2.0313 mm、2.6990 mm和3.5316 mm;随着载荷的增大,其最大位移增加,且增量呈增大趋势。对比各方案最大应力计算结果可知,方案一的最大应力也是各方案中最小,达到56.461 MPa,方案二最大,达到88.905 MPa。图9为方案一在两种工作阻力作用力下的应力云图。

图9 方案一扭转工况应力云图Fig.9 Stress cloud diagram of the scheme one with torsion
综合以上三种方案的计算结果可以看出,方案一质量减少了17.24 kg,最大位移较优化前增加0.3294 mm,变化最小;方案二质量减少19.50 kg,减小量更多,但最大位移达3.8384 mm,最大应力达88.523 MPa,相对变化较大;方案三的应力值变化较小,但最大位移达到了3.6623 mm。由于方案一的扭转变形最小,最大应力变化也最小,达到了相对较优的设计目标,因此,选方案一作为横臂的优化方案,进一步分析其动态性能。
3 模态分析
模态分析是结构动态分析的重要方法,通过模态分析掌握机械结构各阶模态的固有频率和振型等特性,是进行瞬态响应分析和谐响应分析等动力学分析的基础[12]。把横臂四个连接孔设置为固定约束,在ANSYS环境下,分别对原方案和方案一进行模态分析,采用完全法计算得到其前六阶固有频率和固有振型。图10为原方案与方案一固有频率对比,图11、图12分别为原方案与方案一的前六阶振型云图。

图10 固有频率对比Fig.10 Natural frequency comparison diagram

图11 原方案横臂前六阶振型Fig.11 First six mode shape of the beam of the original scheme
由图10可知,方案一各阶固有频率较原方案均有所下降,其中第一、二阶固有频率变化较小,三到六阶固有频率变化较大。对比振型云图可知,原方案和方案一第一阶振型均表现为绕Z轴沿X方向的弯曲,二阶模态振型表现为绕X轴沿Z方向的弯曲。两方案前四阶振型基本相似,五、六阶弯曲扭转组合振型有所不同。由于去除了部分区域,较高阶扭转振型的奇点位置发生了一些移动。提取原方案与方案一横臂X轴、Y轴、Z轴及绕X轴Rx、绕Y轴Ry、绕Z轴Rz这6个方向有效模态质量,如表1和表2所示。
由表1与表2可知,方案一与原方案相比,各阶自由度有效模态质量均发生了一些改变,但是相对较小,其中前四阶占主要模态质量的自由度方向基本没有改变,第五阶的转动自由度最大的仍然是Rz,Rx与Ry大小顺序发生了颠倒,第六阶的转动自由度最大的仍然是Rx,Ry与Rz大小顺序发生了颠倒,结合两方案横臂模态振型图和各阶有效模态质量分析可以得出:
一阶模态中均是X和Rz方向的值较大,表现为绕Z轴沿X方向的弯曲;二阶模态中均是Z和Rx方向的值较大,表现为绕X轴沿Z方向的弯曲;三阶模态中均是Ry和Rz与X方向值较大,主要表现为绕Y轴的扭转,其次是绕Z轴沿X的弯曲;四阶模态中Z与Rx方向的值较大,表现为绕X轴沿Z和绕X轴沿Y方向的弯曲;五阶模态中原方案为Rz与X和Ry方向值较大,表现为绕Z轴沿X方向的弯曲和绕Y轴的扭转,方案一Rz与X和Rx方向值较大,表现为绕Z轴沿X方向的弯曲和绕X轴的扭转;六阶模态中原方案Rx与Ry和Z方向的值较大,表现为绕Y轴沿Z方向的弯曲和绕X轴扭转,方案一Rx与Rz和X方向的值较大,表现为绕Z轴沿X方向的弯曲和绕X轴扭转。

图12 方案一横臂前六阶振型Fig.12 First six mode shape of the beam of the scheme one
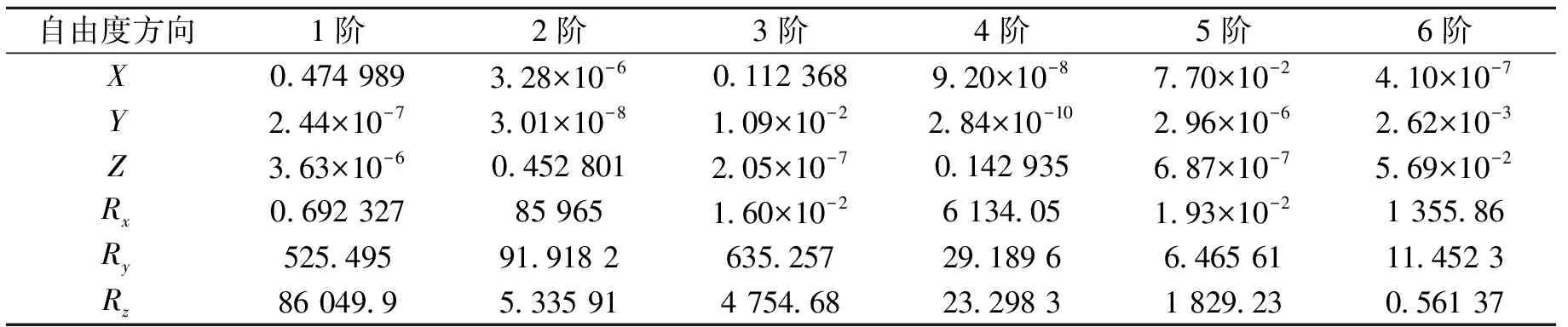
表1 横臂原方案各方向有效模态质量Tab.1 Effective modal mass in each direction of the beam of the original scheme
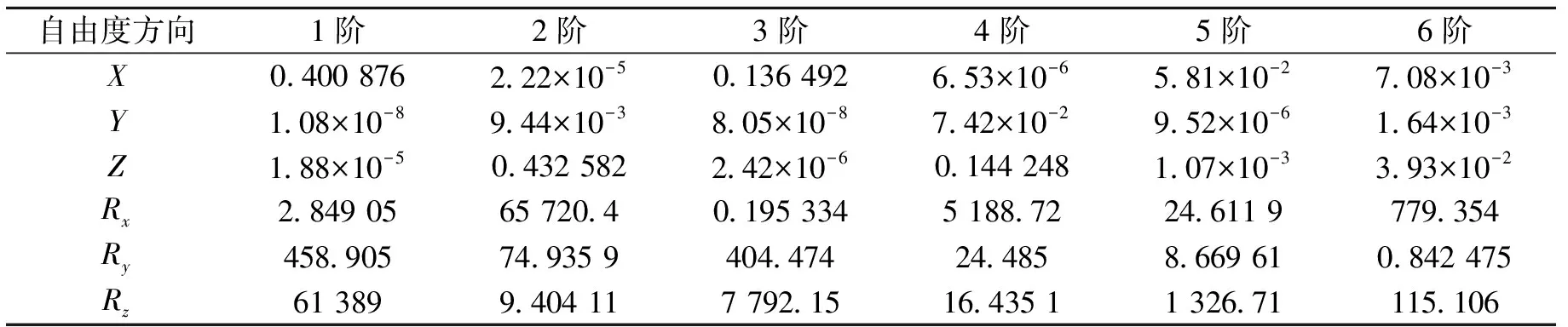
表2 横臂方案一各方向有效模态质量Tab.2 Effective modal mass in each direction of the beam of the scheme one
总结以上结果,原方案与方案一的模态参数结果如表3所示,方案一固有频率略有下降,前四阶振型基本一致,五六阶振型发生了部分改变。

表3 原方案与方案一模态对比Tab.3 Mode comparison between the original scheme and the scheme one
4 结 语
在分析光伏板布局特点的基础上,设计开发了光伏板清洁装置,给出了设计方案。针对当前清洁装置过重的问题,对机械臂的横臂进行结构优化设计,结合拓扑计算,对所提出的三种优化方案进行力学性能对比,选择出最优设计方案。对比给出了最优方案与原方案前六阶固有频率与固有振型等模态参数的变化,对较优方案进行谐响应分析和瞬态响应分析。由计算结果可知,方案一可较好地满足工作需要,实现了横臂结构优化设计,为清洁装置的进一步优化提供了参考依据。

