SHADE算法在无线传感器网络节点分布优化的应用

张建波，王金玉

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

0 引言

无线传感器网络(wireless sensor networks,WSN)是一种分布式传感网络，由部署在监测区域内的大量微型传感器节点组成[1]。无线传感器网络目前广泛应用于标量数据采集。随着电子工业的发展，WSN在抗震救灾、医疗保健方面发挥着越来越重要的作用。

WSN的高效稳定性主要依赖于传感器节点分布，使之能够以最少的传感器节点感知最大的目标区域。文献[2]对人工鱼群算法进行了改进，采用适应度值对鱼群进行分类，针对适应值差的鱼群，引入变异因子。文献[3]将混沌运动引入粒子群算法，帮助粒子群逃逸局部最优，但迭代次数过多，平均覆盖率不高。文献[4]针对人工蜂群算法中雇佣蜂的搜索方式在高维问题进化速度慢的问题，引入差分进化算法，提高了算法运行速度。文献[5]将分层机制引入蜂群算法，可提高网络覆盖率，但迭代次数过多。

针对无线传感器节点优化问题，本文以网络覆盖率为目标函数，采用基于历史成功的自适应参数差分进化算法对目标函数进行求解。为了验证本文所提算法的有效性和高效性，通过MATLAB仿真，分别与人工蜂群差分进化(SSDE)算法和差分进化(differential evolution,DE)算法进行对比。

1 WSN覆盖模型

将二维被测区域S离散化为(m×n)个网格点，设网格点的坐标Ki=(xi,yi),i=1,2,…,m×n。若有N个无线传感器节点位于WSN网络中，则任意节点的坐标Lj=(xj,yj)，j=1,2,…,N，且传感器监测半径均为r。网格点Ki到传感器节点Lj的距离为:

(1)

本文采用布尔感知模型[6]，则传感器节点Lj感知任意网格点Ki的概率为：

(2)

WSN中所有传感器节点的覆盖行为相互独立。一个传感器节点可以被多个传感器节点同时感知。因此，对于被测区域中的网格点，被WSN覆盖的联合概率为:

(3)

被测区域每个网格点的覆盖状态均可由式(3)计算得到。由于WSN网络中每个传感器节点的覆盖范围呈圆形分布[7]，为了简化计算，将WSN覆盖的所有网格点与离散后的所有网格点数的比值定义为被测区域的覆盖率。WSN覆盖模型的目标函数如式(4)所示。

(4)

2 自适应参数差分进化算法

基于历史成功的自适应参数差分进化(success-history based parameter adaptation for differential evolution,SHADE)算法是DE算法的一种高级变体，它使用了成功的控制参数设置的历史记忆来指导未来控制参数值的选择[8]。这使得采用SHADE算法求解非线性优化问题时能够精确和快速收敛到全局最优。标准DE算法的迭代有四个基本步骤：初始化，变异，交叉和选择。

2.1 初始化

DE优化过程的第一步是通过为每个个体的决策向量分配随机值，来创建候选解的初始种群。这些值必须位于决策向量的可行范围内(最大值和最小值之间)。初始化第i个决策向量的第j个分量为：

(5)

式中：randi,j[0,1]为0到1之间均匀分布的随机数；上标0表示初始化。

2.2 变异

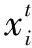
(6)

(7)

2.3 交叉

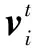
(8)

式中:K为{1,2，...，d}中的任意自然数。

2.4 选择

(9)

在本文中，针对网络覆盖目标函数，为了使网络节点覆盖率最大化，适应度函数表示为：

(10)

2.5 自适应参数交叉率和比例因子

(11)

(12)

控制参数如表1所示。SHADE算法保留H条参数，以便在搜索过程中引导控制参数实现自适应。即使某些子代的SCR、SF含有一组较差的值，存储在前一代存储器中的参数也不会受到影响。按式(13)～式(14)更新历史存储器M。

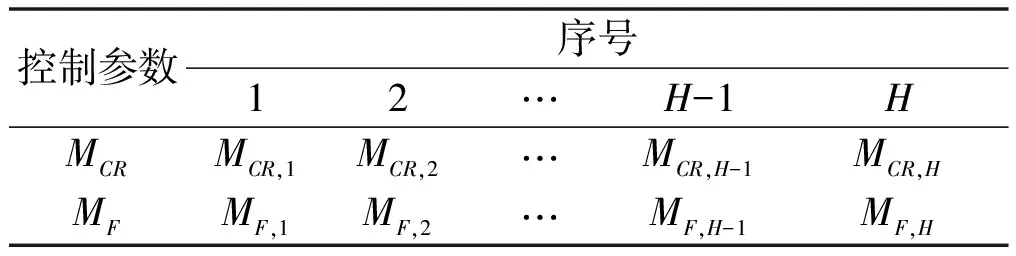
表1 控制参数

(13)

(14)

式中：MEANWA(SCR)和MEANWL(SF)分别为SCR的权重均值和SF的权重Lehmer均值。

初始化索引k=1，每当有一对新的SCR和SF插入存储器时，索引k=k+1。当t代所有个体都不能产生比父代更好的试验向量时，存储器不更新。

2.6 SHADE算法在WSN优化中的主要步骤

SHADE算法在WSN优化中的主要步骤如下。

①初始化算法。设定种群规模Np、最大进化代数Tmax、决策变量维数d等基本参数。

③按照式(10)计算适应度值。

⑤停止标准。判断是否达到最大进化代数Tmax。如果是，则停止并输出最优解；如果不是，则转到步骤②。

3 试验仿真

3.1 参数设置

通过MATLAB进行仿真，采用SHADE算法对WSN优化目标模型求解。被测区域S为100 m×100 m的正方形区域，区域离散化步长为1 m；假设有50个传感器分布在被测区域S内，每个传感器节点的感知半径为10 m。SHADE初始化参数：种群规模Np为200，Tmax为500，决策向量维度d为5，CR和F为0.5。为了验证本文算法优越性，分别采用SSDE和DE对WSN优化问题进行对比，被测区域S不变，l为100，Gmax为500。

3.2 算法性能分析

分别采用SHADE、SSDE和DE对WSN优化目标函数进行求解，三种算法收敛曲线如图1所示。

图1 三种算法收敛曲线

由图1可知，应用DE算法迭代次数最多且覆盖率最低，这是因为DE原理简单，控制参数少但是算法局部搜索能力较弱，在有限时间内很难保证获得全局最优解。SSDE在DE算法中引入人工蜂群搜索策略，使其快速跳出局部最优；但该方法存在疏于开发的问题，收敛速度较慢。SHADE所需迭代次数在三种算法中最少，同时覆盖率也最高。这是因为该方法采用历史存储器M来储存控制参数，避免陷入局部最优解，加快了算法收敛速度。

为了进一步验证算法性能，改变WSN中传感器节点数目，得到三种算法覆盖率随节点变化曲线，如图2所示。

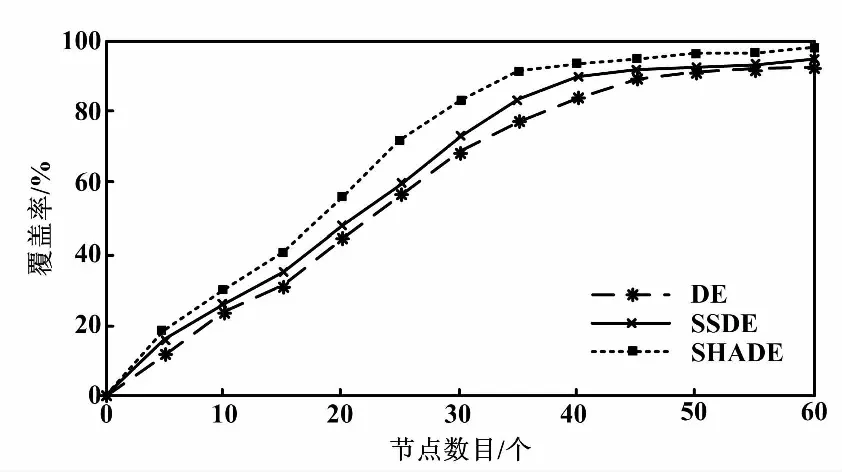
图2 覆盖率随节点变化曲线

从图2可以看出，随着节点数目的变化，SHADE覆盖率均高于SSDE和DE。当节点数为60时，SHADE的覆盖率达到99.8%，而SSDE和DE分别为94.4%和91.3%。

3.3 优化结果分析

将三种算法各运行500次，统计其平均覆盖率、最差覆盖率、覆盖率标准差以及达到最优解时平均迭代次数，所得优化结果如表2所示。

表2 三种算法优化结果

SHADE优化前后分布结果如图3所示。

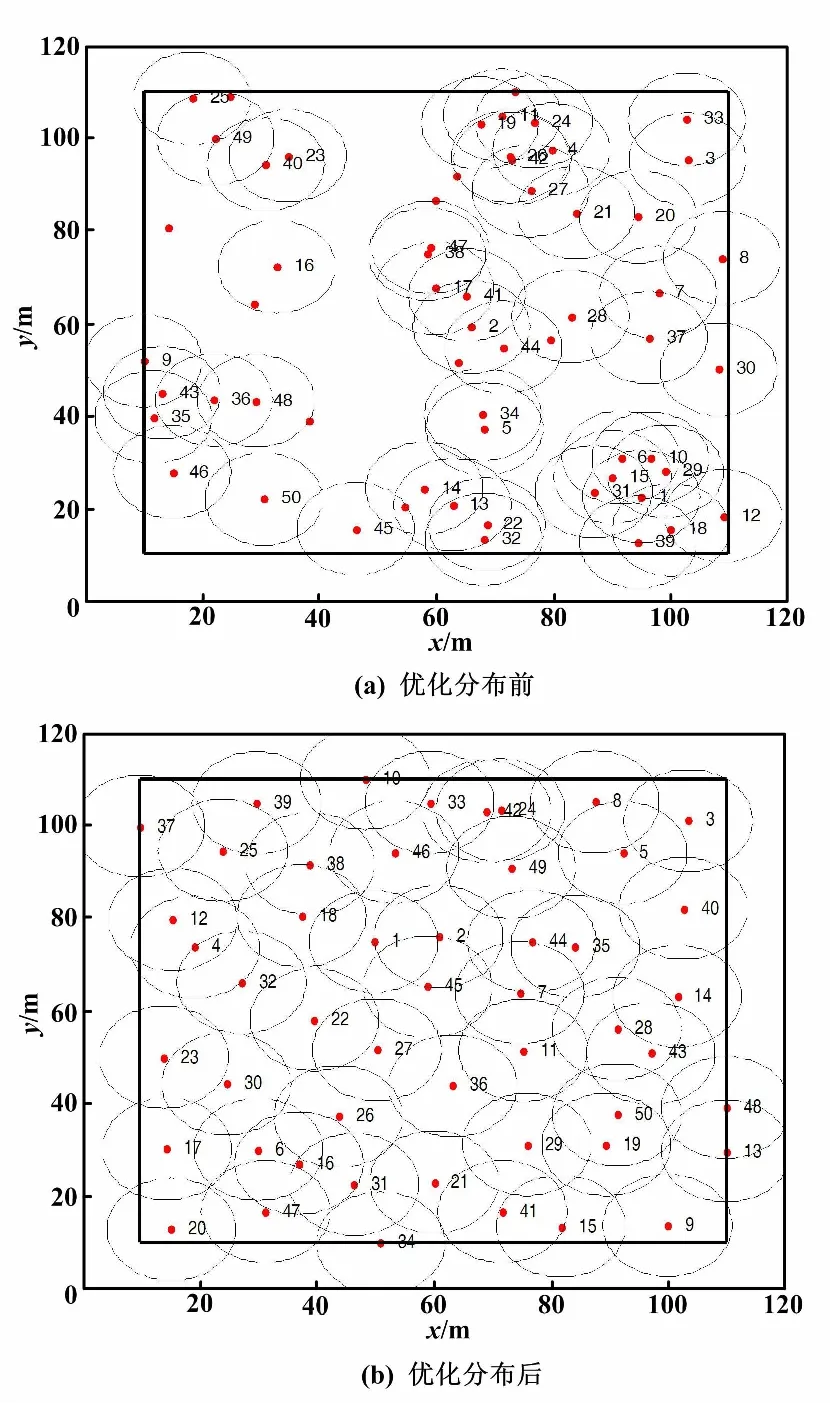
图3 SHADE优化前后分布结果图

从表2可以看出，SHADE在三种算法中的每项指标都优于SSDE和DE。SHADE的平均覆盖率对比SSDE和DE分别提高了1.88%、5.17%。这是因为SHADE能够避免算法早熟、快速跳出局部最优值，提高了算法鲁棒性，获得较高的覆盖率。另外,SHADE的平均迭代次数分别是SSDE的47.3%、DE的34.6%。优化结果证明了SHADE能够快速收敛到全局最优解，并能保障算法精度。初始节点网络中存在大量盲区和节点覆盖冗余。经过SHADE对节点优化之后，传感器节点能够基本覆盖被测区域，进一步保障了WSN的服务质量。

4 结束语

本文利用SHADE算法对无线传感网络分布优化问题进行了研究，通过仿真结果验证了其有效性和高效性。SHADE通过保存交叉率和比例因子，自适应地引导差分进化算法，提高了算法的鲁棒性。针对无线传感器网络优化问题，SHADE能够在较少的迭代次数下获得较高的覆盖率，并可在节点数为60时，实现99.8%的目标区域覆盖。未来将考虑WSN中传感器节点自组织能力，使其能够更好地适应实际需要。