并链式非完整机械臂机构设计及运动规划
冷丽姣,谭跃刚,李 亮,钱冠杰
(1.武汉理工大学 机电学院,湖北 武汉 430070;2.宝鸡文理学院 机械工程学院,陕西 宝鸡 721007)
1 引言
在分析力学中,非完整系统是指其约束方程中包含有坐标对时间的导数的系统,即其约束限制系统的速度或加速度[1]。这类非完整机械系统的自由度数目少于其位形空间维数,表现出欠驱动特性,因此可用较少的控制输入来确定其在较多空间维数的位形空间内的运动。驱动装置的减少有利于设计出结构更紧凑,重量更轻的多关节机械臂,因此非完整机械臂的研究对开发轻小型机器人、医疗机器人、多指灵巧手等有重要的实际意义。
典型的非完整机器人系统有轮式移动机器人、宇宙机器人、体操机器人、水下机器人等,这些机器人系统具有的非完整性和非线性,确定了其运动控制的特点。现有的非完整机械系统研究主要集中于非完整力学以及对现有的非完整系统的路径规划和控制,对新型非完整机器人系统的设计与开发在国内外较为少见。
河村隆基于动物猫在空中下落过程的运动特性分析,提出了一种具有非完整约束性的机器猫[2],因其模型在空中下落过程中可以保持角动量守恒,从而使得机器猫具有非完整特性。文献[3]利用摩擦球矢量分解合成机构开发了一类二维空间内的非完整机器人,这种机器人模型可以转换成链式结构,从而利用链式系统的运动控制方法实现对其运动控制。文献[4-5]中提出了移动机器人路径规划局部最小问题的解决方案;文献[6]中给出了一种RRT(快速搜索随机数算)方法用于解决移动机器人的路径规划问题,并引入目标偏向的思想,克服了以往RRT计算代价较高的问题。
这里是采用摩擦圆盘运动合成分解机构作为关节传动部件,并采用双万向节以并链方式为各个关节传递运动,提出了一种仅由两个控制电机驱动的并链式四关节非完整机械臂。该系统结构简单紧凑,并表现出非完整约束性,为多关节机械臂的驱动单元数与手臂质量相冲突的问题提供了有效的解决方案。通过对其运动学分析和模型的链式变换,给出了非完整性和可控性的证明。在链式空间运用多项式输入法对其进行运动规划,得到一条可行路径轨迹,再通过链式逆变换将轨迹映射回关节空间,完成关节空间内从初始位形至目标位形的运动控制。
2 并链式非完整机械臂机构
2.1 摩擦圆盘运动原理
在下图1(a)中,当半径为r的摩擦轮绕I轴以角速度wi转动时,摩擦轮与转盘之间只有纯滚动,则转盘将以一定的角速度wo绕O轴转动。摩擦轮与转盘相互垂直,在此前提下,摩擦轮还可以绕自身轴心与两者接触点M的连线作相对于摩擦盘的旋转。当旋转过夹角α时,两者在接触点M处的线速度矢量图,如图 1(b)所示。

图1 摩擦圆盘运动合成分解机构Fig.1 Friction Aisc Movement Decomposition Mechanism
则存在下面的关系式:

可得:

式中:R—摩擦轮与转盘的接触线M到转盘中心的距离;vi—摩擦轮在接触点处的线速度;vo—转盘在接触点处的线速度。
从关系式(1)可以看出,摩擦轮与转盘之间的传动比可以通过调节α夹角来调整,因此定义夹角α为传动偏角。
摩擦轮在转盘上因滚动产生的相对运动是由相对位形变化而确定的,依据这种相对位形可变的两摩擦圆盘,设计的摩擦圆盘运动合成分解机构具有非完整约束特性[7]。
2.2 并链式非完整机械臂机构设计
在机械臂的每个关节处设置一组摩擦圆盘机构,其中,摩擦轮与前一关节固连,转盘与后一关节固连,当关节角变化时,也就是摩擦轮与转盘之间的夹角变化,两者的传动比也随之变化。建立的并链式四关节机械臂机构模型图,如图2所示。

图2 并链式四关节机械臂机构Fig.2 Structure of Double-Chain Four Joints Manipulator
电机2的转动直接驱动关节1绕轴线转过角度θ1,由于摩擦轮1通过侧板与机架固定,而转盘1固定在第一关节,所以电机2就控制了关节1的转角θ1,并且相当于在摩擦轮与转盘的摩擦传动中加入了一个θ1的传动偏角。电机1一方面通过齿轮来驱动摩擦轮,摩擦轮因滚动摩擦带动转盘转动,转盘经同步带带动关节2转动角度θ2,与此同时在关节2处的摩擦轮与转盘之间加入一个θ2的传动偏角;另一方面通过双万向节将能量传递到后面的关节,后面的关节传动依次类推。因此实现了两个电机驱动四个关节的目的。并链式机械臂的运动示意图,如图3所示。

图3 并链式四关节非完整机械臂传动示意图Fig.3 Transmission Sketch of Double-Chain Four Joints Manipulator
在并链式机械臂机构的设计中,以下几个问题值得注意:
(1)摩擦轮与转盘之间应具有足够的摩擦力,否则就不能有效、可靠、准确地进行运动传递。可以通过选用摩擦系数大的材料和适当增加接触处的正压力来保证足够的摩擦力。
(2)保证摩擦轮与转盘的接触点位于关节轴线上,如图4(a)所示。若没有达到位置要求,当关节转动一定角度时,摩擦轮就会在转盘上产生滑动,导致摩擦轮与转盘的接触点到转盘中心的距离发生变化,也就是式(1)中的R值变化,这样不仅会影响正常的传动,也使得传动比无法计算。解决方法是在提高零件加工精度的同时提高其安装精度。

图4 摩擦轮与转盘接触点位置、双万向节结构示意图Fit.4 The Position of Contact Point of Friction Wheel and Rotary Table and the Diagram of Double Universal Joint
(3)双万向节的输入轴应与输出轴具有相等的转动角速度,即要求双万向节的中心线OO应与关节轴线一致,并且为补偿由于机械臂关节的转动所带来的输入轴与输出轴之间的轴向距离变化,中间轴应做成可伸缩的形式,如图4(b)所示。
(4)为保证结构的紧凑性、轻量化,在满足强度、刚度要求下,连杆外围采用大圆角和中心部位挖槽处理。在水平方向上,双万向节组成的能量主传递链,和摩擦轮、转盘组成的运动传动链距离机械臂边沿距离大致相等,且约等于两传动链之间的间距,以及连杆上下对称布置,使得机械臂的质心接近其几何中心,有利于提高其运动性能。
3 运动学特性分析及链式变换
3.1 运动学建模
四关节非完整机械臂的位形空间由关节转角θi(i=1,2,3,4)和摩擦轮的角位移φ确定,故定义系统的广义坐标矢量为q=[q1,q2,q3,q4,q5]=[φ,θ1,θ2,θ3,θ4],而控制输入仅有两个电机的角速度u1和u2,说明机械臂系统可以由两个控制输入来控制在较多维数的位形空间内运动。根据运动关系可以推导出并链式四关节机械臂的运动学模型:

式中:r—摩擦轮半径值,R与上文定义相同。
3.2 可控性分析
式(2)是无漂移的控制系统形式,此类无漂移仿射系统的可达空间是由分布 Δ(q)=span{p1,p2}张成的,根据系统的可控性条件,如果无漂移仿射系统的可达分布 Δp(q)=span{p1,p2,[p1,p],[p,[p,p]],…}满秩,则该系统是可控的[3]。
2112
式中:[p1,p2]—对向量 p1,p2的李括号运算;[p1,[p1,p2]]—对向量 p1,[p1,p2]的李括号运算。即有
则并链式非完整四关节机械臂的可达空间可表示为:=Δp(q)=span{p1,p2,[p1,p2],[p1,[p1,p2]],
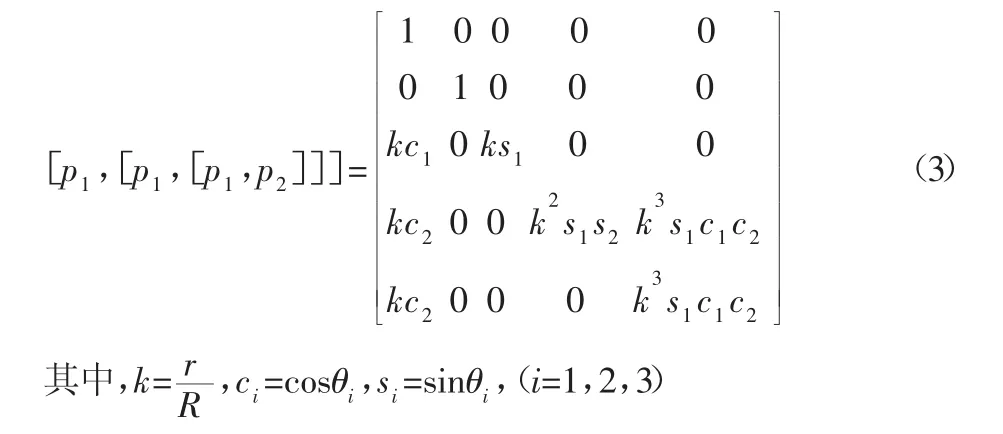
从式(3)可以看出,当 sinθ1≠0,sinθ2≠0,且 sinθ3≠0 时,即θi≠0(i=1,2,3),则有 dimΔp(q)=5,此时矩阵的秩与位形空间维数相等,满足可控秩条件。也就是说当并链式四关节机械臂的工作空间满足θi≠0(i=1,2,3)时,该系统在五维可达位形空间内具有非完整特性,并且是可控的,可以通过两个电机来控制其五个位形变量的运动。
3.3 链式变换特性分析
SØrdalen在研究具有n个拖挂车的轮式移动机器人系统时,给出了具有三角形构造的无漂移仿射系统链式变换的条件和方法[8],即:对于类似于(2)式的无漂移仿射系统:
若在q0的邻域内,光滑函数∀i∈{3,4,…,n},则存在微分同胚的坐标变换式和输入变换式,使得该系统可以变换为链式系统。由此可知,对于该四关节非完整机械臂运动模型式(2),当 θ(ii=1,2,3)≠0时,能够变换成链式结构的坐标变换式(4)和输入变换式(5):


4 并链式四关节非完整机械臂的运动规划
基于链式变换方法的运动规划基本思路是:将系统的初始位形qi和目标位形qf映射成链式空间的初始位形zi和目标位形zf,在链式空间规划出一条从初始位形zi到目标位形zf的路径,再将规划所得的路径通过链式逆变换到关节空间。目前针对链式系统的运动规划方法较为成熟的有:分段常数输入法、三角函数输入法、多项式输入法,相比于其它控制方法,多项式输入法具有积分运算简单,且能控制各变量沿光滑的轨迹运动至目标位形的优点,两个控制输入随时间变化的多项式表达式为:

运动规划的目的就是寻找有界的控制输入u(t),使得系统从初始位形zi,经过规定的时间T到达目标位形zf,即满足等式约束:

结合(6)式对(5)式积分可得各变量的终止位置,分别是关于 b1、b2、b3、b4的表达式:

定义 b=[b1,b2,b3,b4]T,F=[f1,f2,f3,f4]T,给定时间 T 值,将(8)式代入(7)式中可得到关于 b1、b2、b3、b4的非线性方程组,写成牛顿迭代格式有
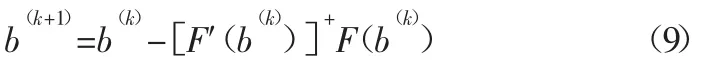
式中:F′(b)—F(b)的雅克比矩阵;[F′(b)]+—F′(b)的伪逆。
给定初始值b(0)之后就可以通过迭代式(9)在MATLAB中计算得到b,将b代入式(8)得到zi(t)的轨迹。将(4)式进行链式逆变换得到各关节角位移关于z变量的表达式如下:
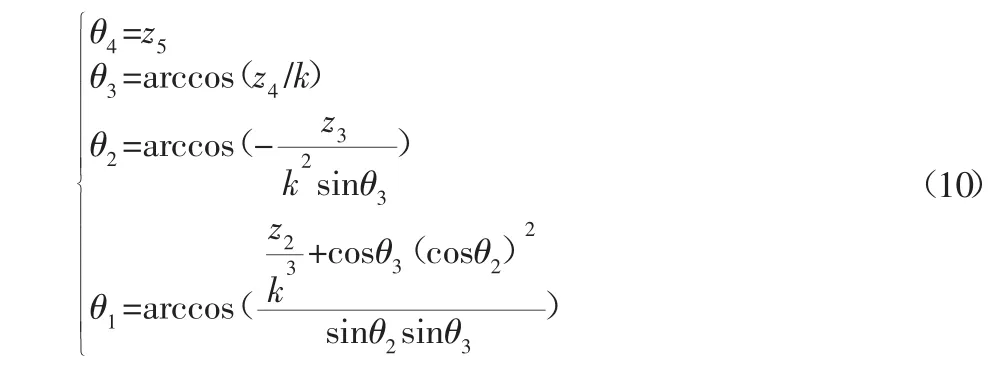
通过式(10)得到四个关节角位移的运动曲线。
5 四关节非完整机械臂的运动分析
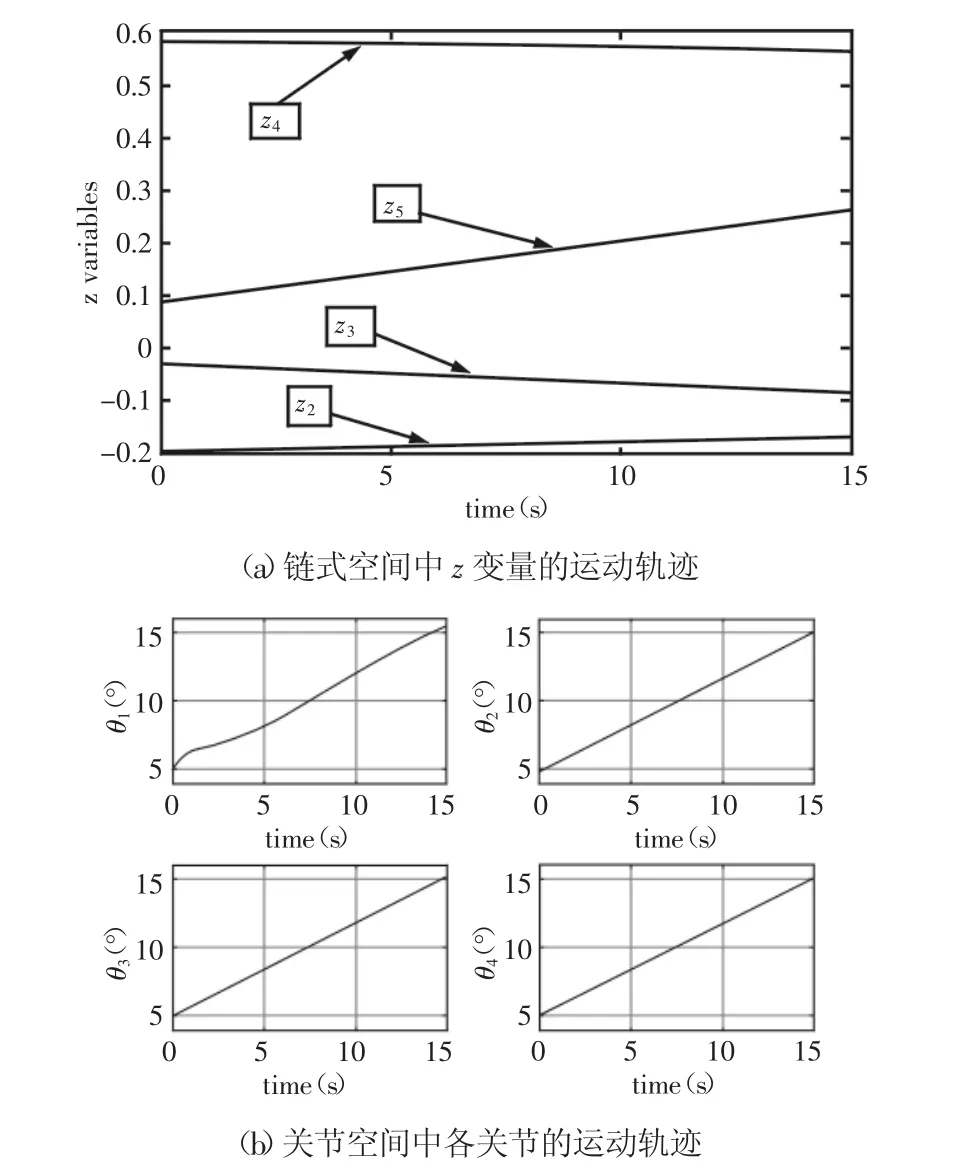
图5 链式空间中z变量、关节空间中各关节的运动轨迹示意图Fig.5 The Diagram of the Motion Trajectory of the z Variables in the Chain Space and the Joints in the Joint Space
在 T=15s时刻,θ1=15.475174°,θ2=14.991161°,θ3=15.000081°,
θ4-=14.999982°。目标位形误差 eθ1=4.7517%,eθ2=0.08849%,eθ3=0.0008%,eθ4=0.00018%。

图6 链式空间中z变量、关节空间中各关节的运动轨迹Fig.6 The Motion Trajectory of z Variables and Joints in the Chain Space
在 T=20s 时刻,θ1=13.8563°,θ2=14.9868°,θ3=14.99997°,θ4=14.99997°。目标位形误差 eθ1=7.6251%,eθ2=0.08784%,eθ3=0.001275%,eθ4=0.0001636%。从两组不同实验数据的目标位形误差结果可以看出,四关节非完整机械臂的后面3个关节在规定的时间内从初始位形能够准确地运动至目标位形,而第一个关节出现的误差较大,是因为其运动轨迹链式逆变换时函数关系复杂,与其他关节运动耦合程度高,求解复杂而容易产生累积误差。
6 结论
基于摩擦圆盘运动分解合成机构,提出的一种新型并链式四关节非完整机械臂,结构简单,通过对运动模型的分析表明其具有非完整性和可控性,且运动模型能够转换成链式系统,并通过在链式系统中运用多项式输入法进行运动规划,机械臂各关节能在规定时间内准确地运动至目标位形,实现了两个电机控制多关节,表现出欠驱动特性。由于当链式空间的运动轨迹通过链式逆变换回关节空间时,会出现逆变换的关节角位移无实解的情况,即出现奇异位形,所以下一步工作将针对于链式逆变换奇异位形的规避展开,可以通过增加对z变量的约束来保证链式逆变换有解来实现。

