基于天河二号超算的网格无关性及并行研究

徐艺峰，李 健，王 杰，范冰丰，王 钢,3+

(1.中山大学 电子与信息工程学院，广东 广州 510000；2.中山大学 先进技术研究院，广东 广州 510275；3.中山大学 光电材料与技术国家重点实验室，广东 广州 510275)

0 引 言

随着计算机软硬件的不断优化和升级，求解问题的规模也日益增大。由于单个计算机的计算和存储能力有限，而大型并行计算机可以实现多个处理部件与设备间的高效互联，因此并行计算逐渐成为求解CFD问题的重要方法[3,4]。“天河二号”是我国自主研发的超级计算机平台，坐落于中山大学的国家超级计算广州中心[5,6]，计算和存储能力世界领先[7,8]，是研究大规模并行计算的最佳选择。

MOCVD(metal-organic chemical vapor deposition)生长过程复杂[9]，包括湍流层流模型、质量与热传输、内部化学反应、三大守恒、工艺参数的设置与薄膜生长条件等[10]。实际生长要对每个因素进行全面而系统的研究因而成本巨大，利用计算流体力学(CFD)通过建立仿真模型来进行数值计算就体现出强大的优越性，并成为了国内外的研究热点[11,12]。通过计算机进行各参数数值的计算，能够得到比较详细的资料，省时省力。

本文通过在“天河二号”上测试Fluent 15.0对MOCVD腔体模型的并行计算能力，探究了网格无关性，得出了最佳并行规模组合，使计算效率大大提高。

1 计算环境及并行计算原理

1.1 计算环境

2017年6月19日，最新的全球超级计算机500强榜单公布，来自中国的超级计算机“神威·太湖之光”和“天河二号”第三次携手夺得前二。随着行业和应用的需要，国家相关部门的重视，中国超级计算机正在飞速发展，在性能与应用上不断迈步[13]。

位于无锡的“神威·太湖之光”由40个机柜、共160个超级节点组成，每个超级节点包含256个计算节点，每个节点装有1个1.5 GHz、260核的SW26010众核处理器和32GB DDR3内存，全系统总Linpack峰值浮点计算能力为为125.4359PFlops[14]。

本次测试中的“天河二号”的硬件系统包含有计算阵列、服务阵列、存储子系统、互联通信子系统、监控诊断子系统等，如图1所示。计算阵列全系统包含125个计算机柜，每个计算机柜包含4个计算插框，每个计算插框包含16个计算刀片，每个计算刀片包含2个计算节点，因此计算阵列一共包含16 000个计算节点。每个计算节点包含：2个Intel(R)Xeon(R)CPU E5-2692 v2 @2.2 GHz 12核心处理器、3个Intel Xeon Phi 31S1P 57核心协处理计算卡、64 GB内存、高速互联接口、2个以太网接口。一个E5-2692处理器Linpack峰值浮点计算能力为0.2112TFlops，一个Phi 31S1P协处理计算卡Linpack峰值浮点计算能力为1.003TFlops，总的峰值性能为3.4314 TFlops。因此计算阵列Linpack峰值浮点计算能力为54902.4TFlops，也就是每秒钟5.49亿亿次[15]。

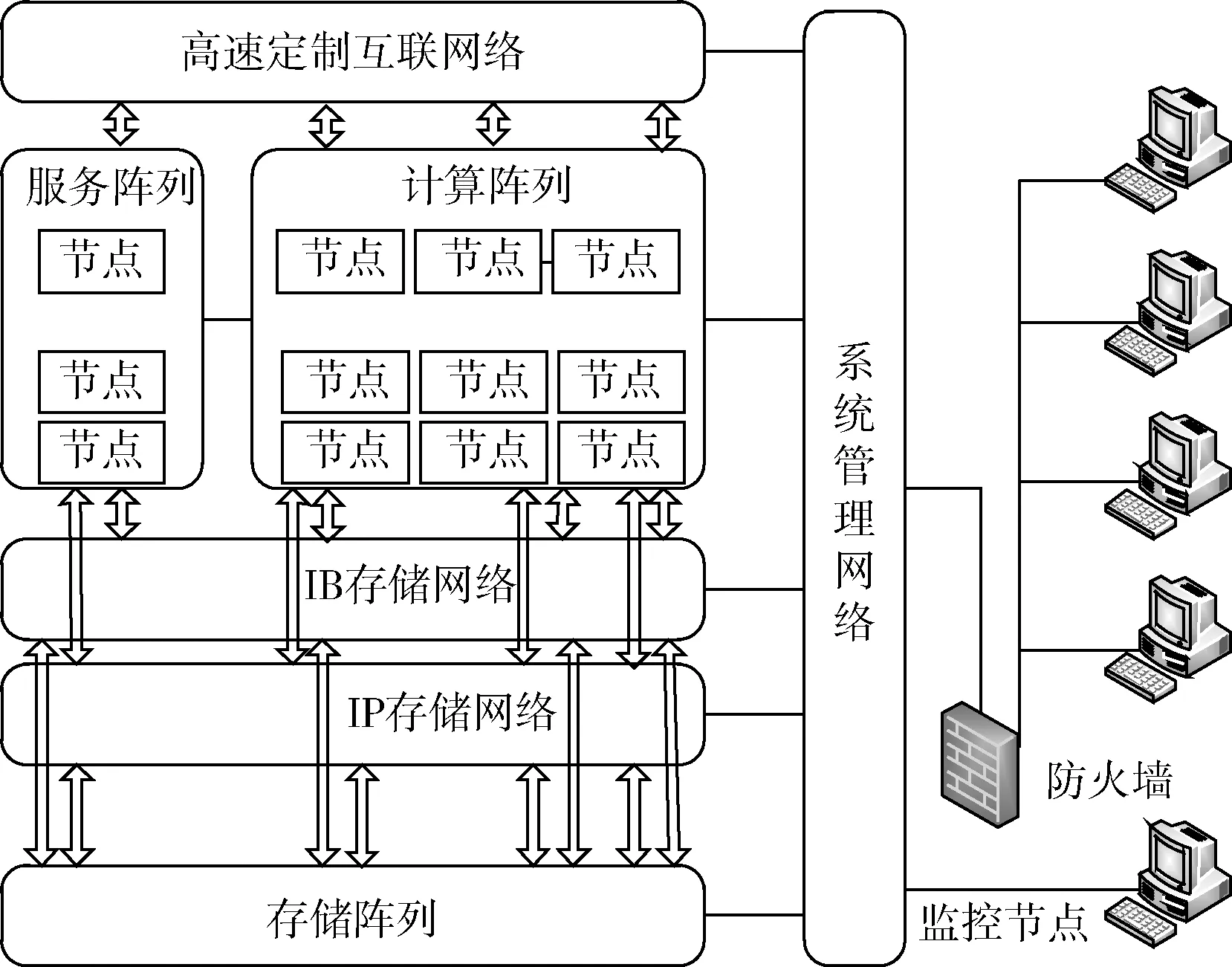
图1 天河二号结构

软件系统包含有系统操作、运行支撑等4种环境。当前操作系统版本为Red Hat Enterprise Linux Server release 6.2。应用开发环境包括串行编程语言、并行开发工具和并行编程模型。并行编程模型定义请参见文献[16]。

1.2 Fluent并行计算

在天河二号超级计算机上的测试采用的是由安世亚太公司(Ansys公司的中国代理商)提供的测试版Ansys15.0。Fluent软件是一个应用于模拟和分析复杂几何区域内的流体流动与传热现象的专业软件，该软件是当今世界CFD仿真领域最为全面的软件包之一[17]。

Fluent并行计算是用多处理器来计算大规模问题，计算可以在一台机器上执行，也可以同时在多个不同机器上执行。并行处理主要目的是为了减少仿真时间，可以使用速度更快的机器，例如更快的CPU，内存，缓存以及CPU和内存之间的通信带宽，也可以使用更快的互联，例如较小的延迟和更高的带宽，还可以使用更好的负载均衡，例如载荷均匀分布以及CPU的运算过程中不会空转。Fluent并行计算的基本原理，如图2所示。Fluent并行处理包括一台主机进程，一系列的计算进程(处理器)以及计算进程之间的相互作用。Cortex功能是处理Fluent的用户界面和基本的图形功能。主机进程不存储任何网格和计算数据，主要解释来自cortex的命令，然后通过socket把这些命令发给计算进程0，计算进程0再将获取的命令传递给其它计算进程。每个计算进程上都有一个MPI(message passing interface)，计算进程之间相互交换数据信息通过MP库实现[18]。

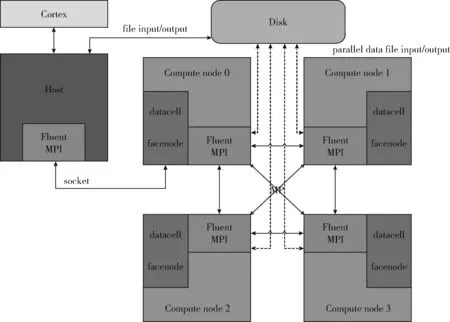
图2 Fluent并行计算结构原理

各计算进程计算之前，需要将整个三维流场区域分成多个计算区域。对网格进行分区域，需要选择分区的方法，设置分区的数量，以及对网格分割的质量进行最优化。分区域的主要目的是为了平衡每个计算区域的网格单元数量、尽量减少各个计算区域边界的表面积以及尽量减少计算区域的数量，确保每个处理器都有相同的负载以及各个计算区域之间数据交换能同时进行。本此测试采用METIS算法进行分区[19]，这种分区方法对计算区域的数量没有限制，该算法将根据实际处理器的数量自动生成相同数量的计算区域。然后分配给相应的各计算进程去计算，由主机进程调度各个处理器的计算，在每一次全区的扫描过程中，由各个处理器完成计算并在边界完成数据交换。最后由主机进程根据收敛准则进行判别，若收敛则计算结束，不收敛则继续迭代求解。

2 MOCVD模型简介及边界条件设定

MOCVD的整个反应腔体为立式旋转基座结构，如图3所示。MOCVD的基本原理是以V族、Ⅵ族元素的氢化物和Ⅱ族、Ⅲ族元素的金属有机化合物作为外延生长的源材料，经过热分解反应与化合反应等一系列化学反应后，在衬底表面沉积出各种Ⅲ-V族、Ⅱ-Ⅵ族化合物半导体薄膜材料[20]。MOCVD腔体原几何模型非常复杂，对原几何模型在不影响流场流动的情况下进行简化，如图4所示，原上盖的两层进气结构简化为一层进气入口，去掉了观察窗等区域。

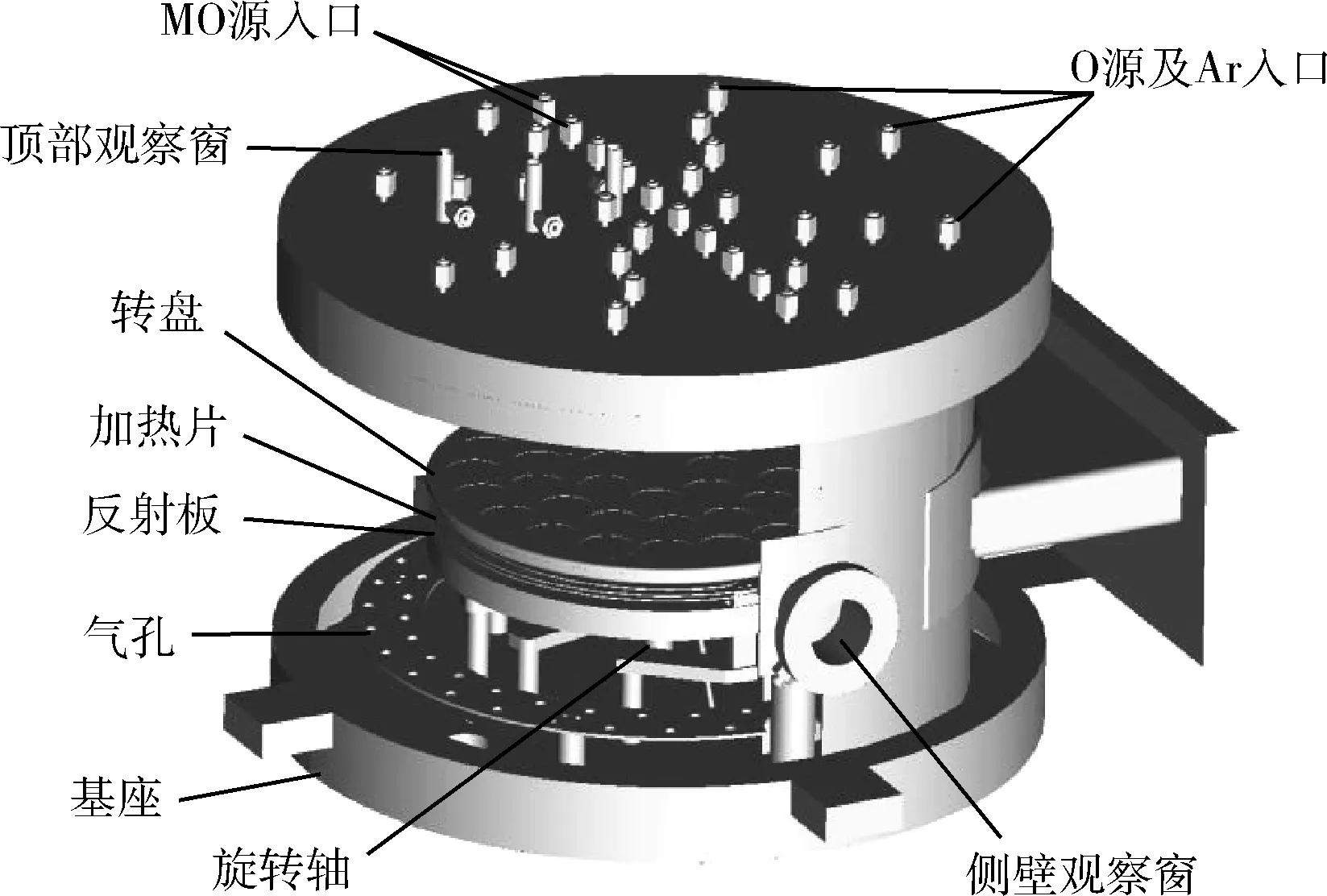
图3 MOCVD反应腔体

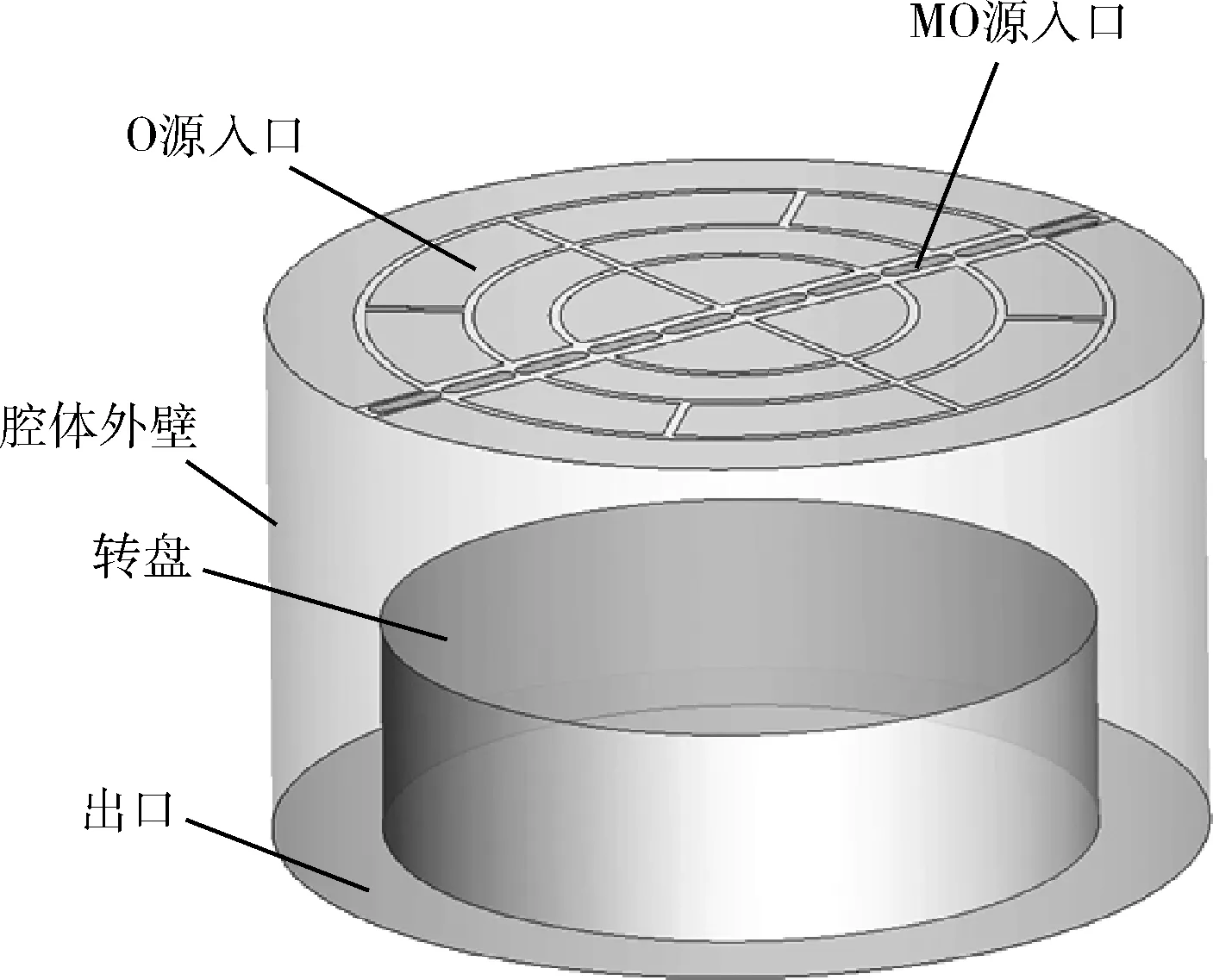
图4 MOCVD反应腔体简化

本文选用SIMPLEC算法来求解控制方程组[12]，根据实际流动状态设置CFD边界条件如下：

(1)MO源入口和O源入口均设置为Velocity Inlet(速度入口)，O源混合气体流量为1560 sccm，O2摩尔百分数为4.6%，MO摩尔百分数为0.22%，MFC1入口流量为147 sccm，MFC2入口流量为632 sccm，MFC3入口流量为747 sccm，MFC4入口流量为575 sccm，MFC5入口流量为173 sccm。

(2)出口设置为Pressure Outlet(压力出口)为0 Pa，腔体内部压强为10torr。

(3)衬底的转速和温度分别为750 rpm和723 k，反应堆内壁和外壁设置为绝热和无滑移的。

3 网格无关性

从理论上来说，当网格数量越密时，模型越准确，但计算量也越大。由于目前的超级计算机是在Linux系统下操作，同时计算所保存的数据特别大，从超级计算机上传和下载数据不便，因此有必要探索网格数量对结果的影响。网格无关性是指，当网格数量达到一定数量时，随着网格数量再次增加，沉积率基本上变化不大的情况[21]。实验中求沉积率的方法，如图5所示，将转盘表面放有硅片的区域沿着径向分成9片圆环，标记为9个点，对每片圆环沉积率求得的平均值即每个点上的沉积率[22]。

本文模型中通过对网格数量作均匀加密处理，计算得出每组Case的9个点的沉积率数值，并比较每组沉积率的相关系数和平均沉积率的误差，以探索网格无关性，具体情况如表1及图6所示。

图5 转盘表面分区

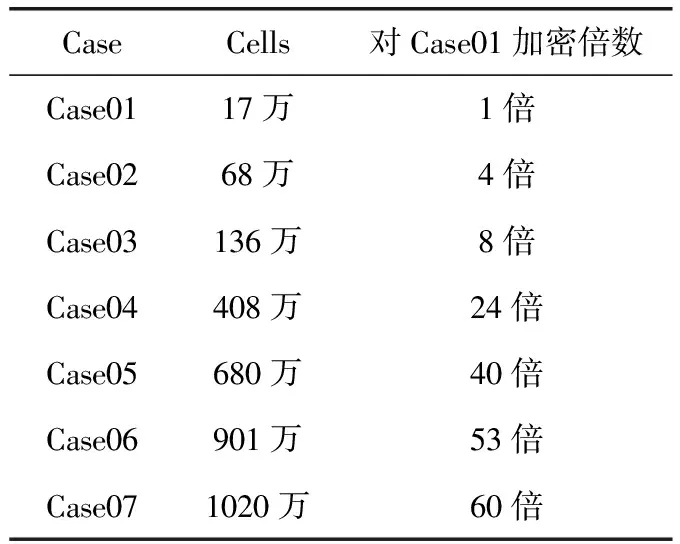
CaseCells对Case01加密倍数Case0117万1倍Case0268万4倍Case03136万8倍Case04408万24倍Case05680万40倍Case06901万53倍Case071020万60倍

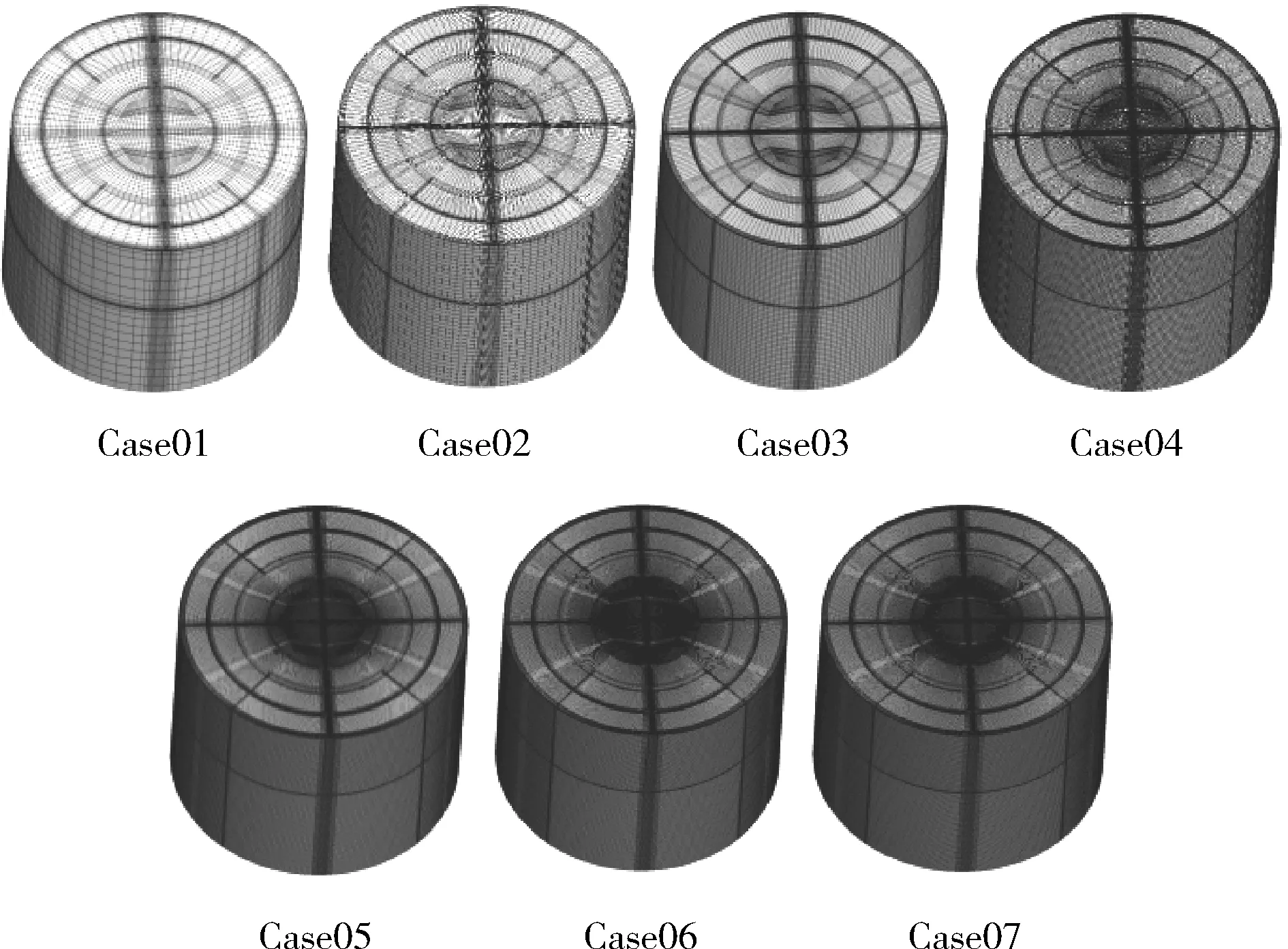
图6 不同网格数量的网格

通过计算加密后的网格，得出每个Case对应每个点的沉积率数值，其中沉积率的单位是μm/h，结果见表2。比较每个Case与Case07之间的相关系数(correl)，即可得出它们间变化趋势的相似程度，而比较每个Case与Case07之间的误差(error)，即可得出它们间平均沉积率数值上的差异程度。从表2中可以看出，对于相关系数，Case01到Case03，相关系数并没有呈增加的趋势，反而下降，表现出了一定的不稳定性，而Case04到Case06，相关系数不断稳定接近于1，因此Case04到Case07的变化趋势相似程度较高。对于误差，Case01到Case03误差较大，约为2%到3%，而Case04到Case06误差缩小近一个数量级，达到约0.5%到0.7%，因此Case04到Case07的平均沉积率数值差异较小。综合以上两点说明，从Case04开始沉积率曲线已经趋于稳定，与Case07之间差异不大，可以认为此时已经达到网格无关性，为了能快速的进行大规模计算，没必要继续做加密处理，因此在进行数值计算过程中选用case04进行计算，而对于没有达到网格无关性的Case，如Case01，由于其误差也小于5%，因此工程上也可以应用它来进行调机，以快速得到结果。

表2 加密网格的计算结果

4 并行计算结果与分析

测试选取的模型是上面提到的两个不同数量级网格单元，并且均是实验常用的MOCVD反应腔体的三维网格模型，具体情况见表3。

表3 MOCVD模型的基本情况

并行计算时间：算法在并行机上求解问题时，从第一个任务进程开始执行到最后一个任务进程执行完毕所需的时间。包含CPU计算、并行开销和算法输入输出所需时间总和。本次测试中，对于问题规模大的情况，如单核计算网格数量大的情况，计算时间是估算值。所有的计算时间均是指从开始迭代到迭代结束为止所用的时间，不包括启动软件以及读入Case的时间，因为启动软件以及读入Case的时间相对比较小，可以忽略不计。

并行加速比： Sn=T1/Tn， 即问题规模不变的情况下并行规模n时的并行加速比，并行规模通常为处理器核数，本次并行规模的核数选取依次为：1、2、4、8、12、16、32、64、128、160、240。

并行计算效率： En=Sn/n， 即问题规模不变的情况下，并行规模核数为n时的并行计算效率，假设单核迭代时，计算效率为1。

首先单独考虑Case A的情况，即问题规模保持不变，如图7所示，发现随着并行规模核数的增加，加速比呈现先增加后减小的趋势，在处理器核数为16时达到峰值，Case B也呈现出相同的趋势，并且在处理器核数为128时达到峰值。加速比增加的原因是多核的并行计算，大大缩短了计算时间。加速比减小的原因是由于并行规模相对于问题规模较大，各个计算区域的信息数据交换非常消耗时间，进程之间数据交换的时间比进程计算的时间要长，从而导致整个并行计算时间相对增加，因此减少分界面以及计算区域的数量可以减少数据交换所需的时间。并且各个计算区域的信息数据交换方式还有待进一步的提高。

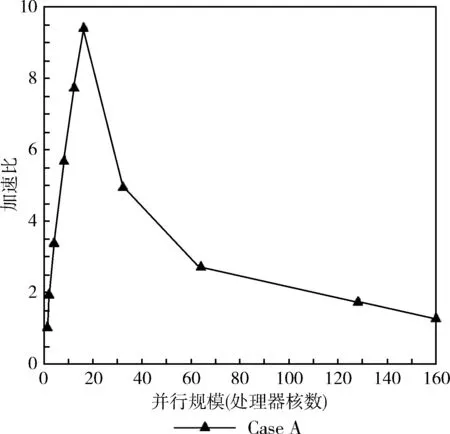
图7 Case A的加速比曲线

对比Case A和Case B的加速比曲线，如图8所示。当并行规模不变时，随着问题规模的增加，加速比逐渐增加，因此对于问题规模比较大的情况，使用多核并行计算会大大缩短计算时间，从而降低数值模拟的周期。问题规模较小时，读入Case的时间可以忽略不计，问题规模较大时，随着并行规模加大，读入Case的时间也相对的减少了。

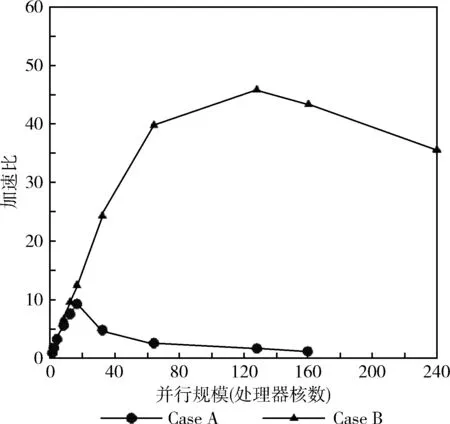
图8 Case B的加速比曲线

实验结论：

(1)由于网格数量大小影响沉积率结果以及计算速度，因此在进行迭代计算之前，对于网格划分时，要充分考虑到网格数量问题，实验结果表明，对于MOCVD腔体模型，当网格数量达到408万时，可以认为已经达到网格无关性。

(2)当问题规模保持不变时，随着并行规模的增加，并行计算的加速比呈现先增加后减小的趋势，计算效率也逐渐降低。对于17万个六面体单元的MOCVD腔体模型，处理器核数为16时计算效率达到最高，加速比达到9，对于408万个六面体单元的MOCVD腔体模型，处理器核数为128时计算效率达到最高，加速比达到45。

5 结束语

本次测试在国家超级计算广州中心的平台上进行，利用天河二号超级计算机的计算资源，由安世亚太公司提供的测试版软件Ansys 15.0。测试验证了网格无关性，并选取了17万个六面体单元和408万个六面体单元的两个MOCVD腔体模型，对MOCVD反应腔体的温度场及流场进行数值模拟，结果表明，前者在处理器核数为16时，加速比达到最高值9，后者在处理器核数为128时，加速比达到最高值45。

通过本次测试可以看出，对于MOCVD腔体数值模拟的大规模计算问题，由于需要计算的工况很多，而且网格数目巨大，利用普通的计算机很难完成，因此超级计算机并行计算成为了理想选择。Fluent在天河二号上的应用尝试，大大提高了仿真实验的计算效率，适用与大规模并行计算，结果可为后续计算提供参考。